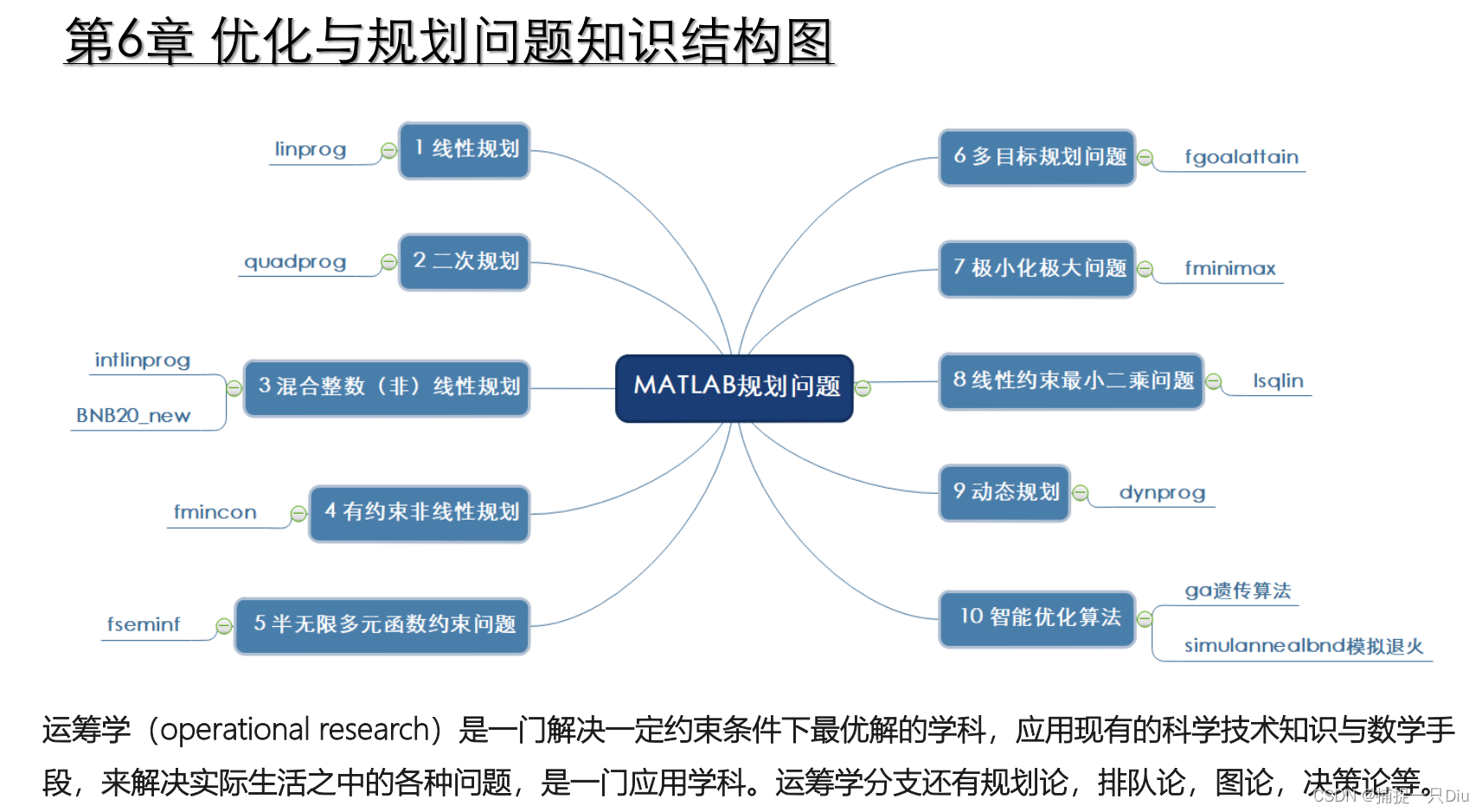
一、线性规划



% 线性规划(Linear programming, 简称LP)
fcoff = -[75 120 90 105]; % 目标函数系数向量
A = [9 4 7 54 5 6 105 10 8 53 8 9 77 6 4 8]; % 约束不等式系数矩阵
b = [3600 2900 3000 2800 2200]'; % 约束不等式右端向量
Aeq = []; % 约束等式系数矩阵
beq = []; % 约束等式右端向量
lb = 50*ones(4,1); % 决策变量下限
ub = []; % 决策变量上限
options = optimoptions('linprog','Algorithm','dual-simplex','Display','iter'); % dual-simplex单纯性法
[x,fval,exitflag,output,lambda] = linprog(fcoff,A,b,Aeq,beq,lb,ub,options)
fval = - fval 

fcoff = [2 1 3 2 1 3 4 1 3 2 1 3 2 1 1 2 1 3 2 2]'; % 按一列一列录入
A = [1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 00 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 00 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 00 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1];
% A1 = repmat(eye(4),1,5)
b = [60 40 50 55]';
Aeq = [1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1];
beq = [20 35 33 34 30]';
lb = zeros(20,1);
% options = optimoptions('linprog','Algorithm','interior-point'); % interior-point内点法
options = optimoptions('linprog','Algorithm','dual-simplex'); % dual-simplex单纯性法
[x,fval,exitflag,output,lamda] = linprog(fcoff,A,b,Aeq,beq,lb,[],options)
x = reshape(x,4,5)二、二次规划

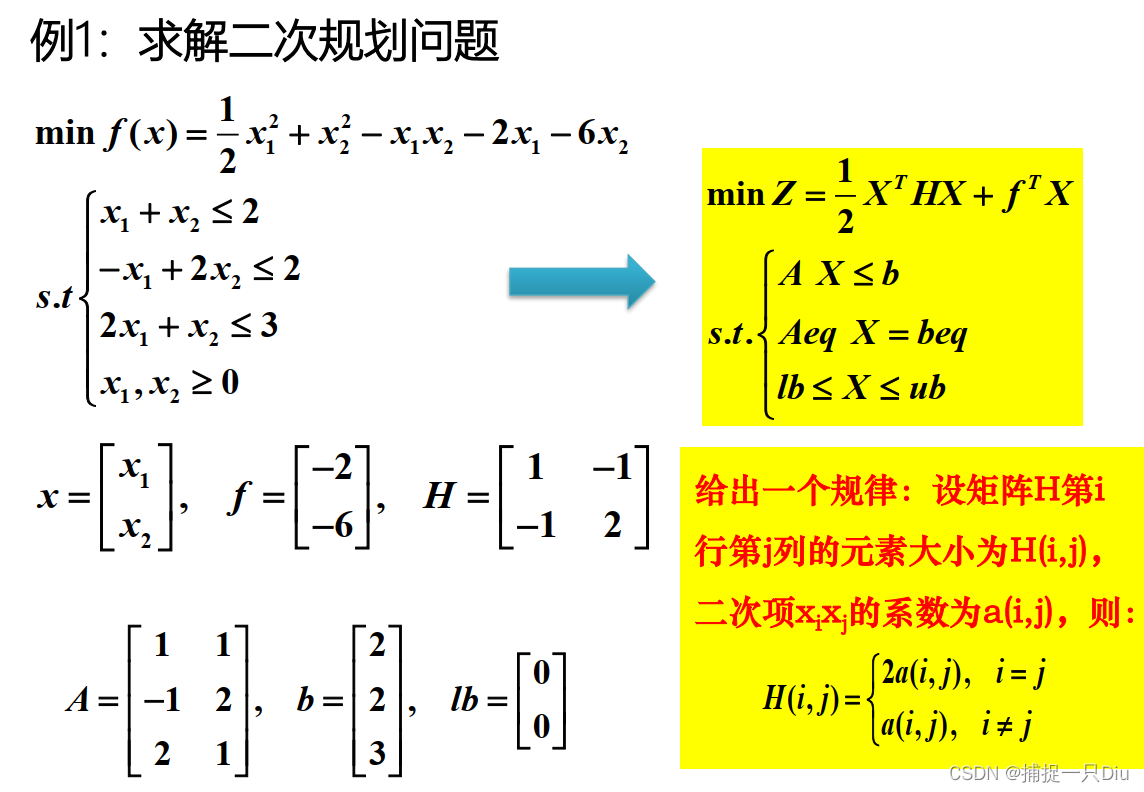
H = [1 -1; -1 2];
f = [-2; -6];
A = [1 1; -1 2; 2 1];
b = [2; 2; 3];
lb = [0; 0];
options = optimoptions('quadprog','Algorithm','interior-point-convex','Display','iter');
[x,fval,exitflag,output,lambda] = quadprog(H,f,A,b,[],[],lb,[],[],options) % 若不加options,则可以省略x0三、混合整数(非)线性规划

intcon: int condition
决策变量0-1问题:
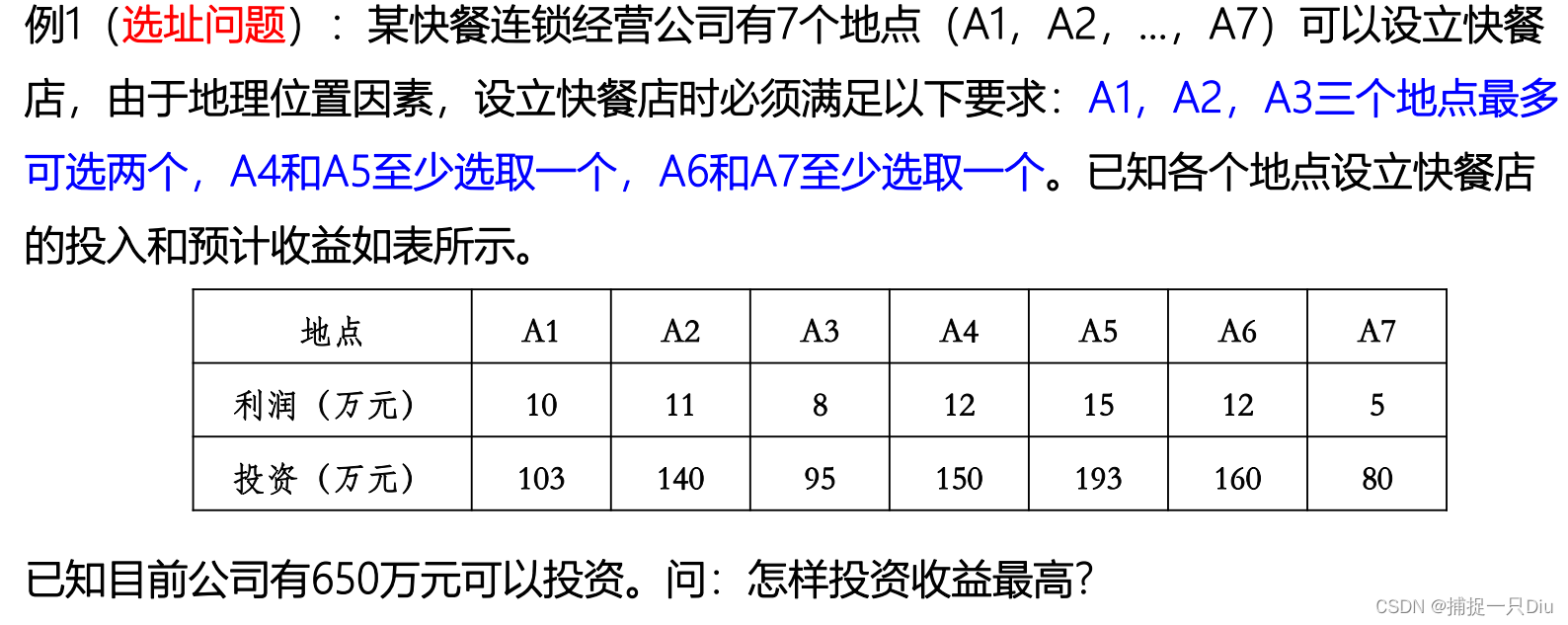

fcoff = [-10 -11 -8 -12 -15 -12 -5];
intcon = 1:7;
A = [103 140 95 150 193 160 80; 1 1 1 0 0 0 0; 0 0 0 -1 -1 0 0; 0 0 0 0 0 -1 -1];
b = [650;2;-1;-1];
Aeq = [];
beq = [];
lb = zeros(7,1);
ub = ones(7,1);
[x,fval,exitflag] = intlinprog(fcoff,intcon,A,b,Aeq,beq,lb,ub)
maxf = -fval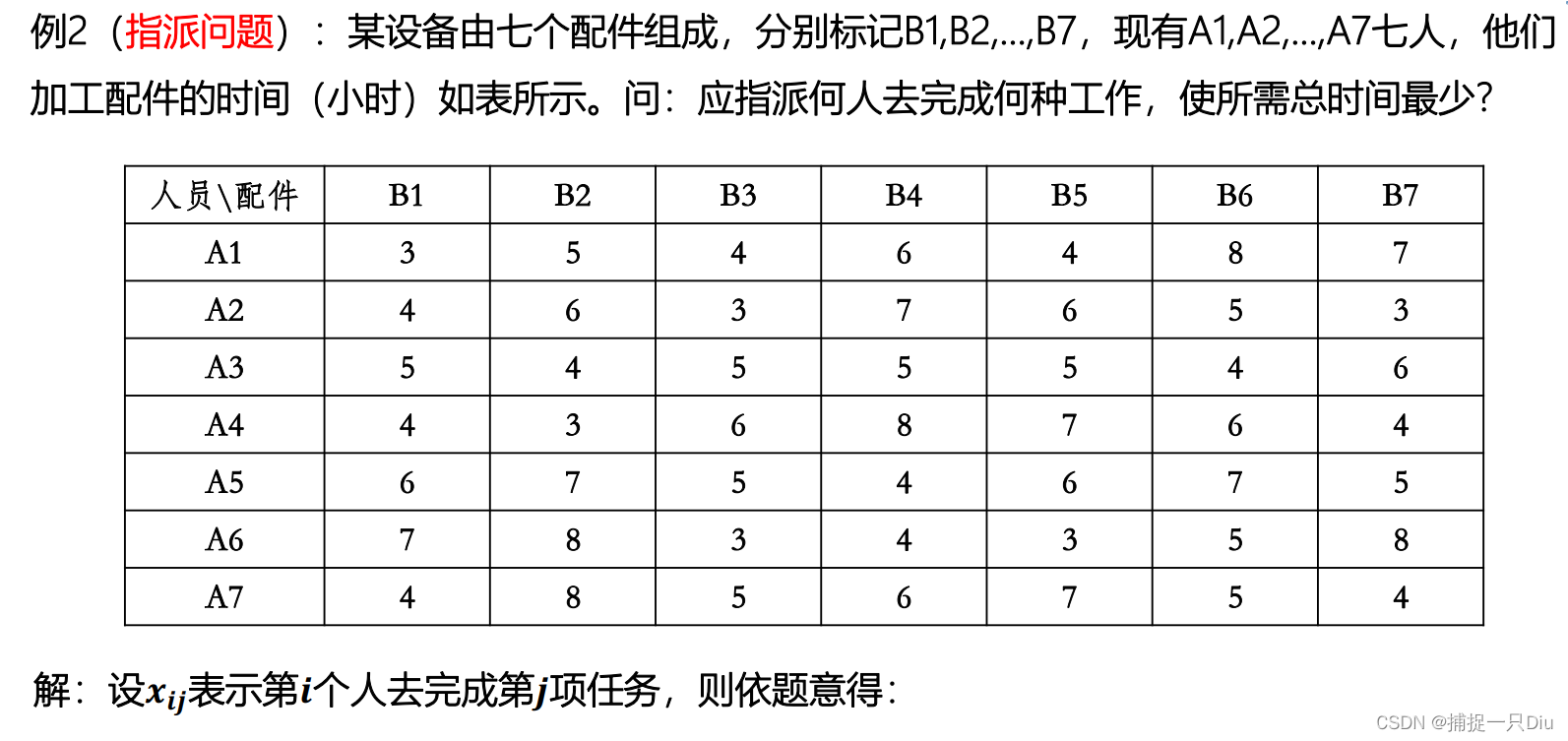

function [x,fval,exitflag] = intlinprog_ex2()designate_data = xlsread('designate.xlsx',1,'B2:H8');fcoff = designate_data(:); % 目标函数系数向量intcon = 1:49;A = [];b = [];Aeq1 = zeros(7,49);for i = 1:7Aeq1(i,(i-1)*7+1:i*7) = 1; % 起点1 8 15 22...,终点7 14 21 28...endAeq2 = repmat(eye(7),1,7);Aeq = [Aeq1;Aeq2];beq = ones(14,1);lb = zeros(49,1);ub = ones(49,1);[x,fval,exitflag] = intlinprog(fcoff,intcon,A,b,Aeq,beq,lb,ub);x = reshape(x,7,7);
end

function [C,Ceq] = stBNB_fun1(x)Ceq = []; % 非线性约束等式% C表示非线性约束不等式C = [x(1)^2 + x(2)^2 + x(3)^2 + x(4)^2 + x(1) - x(2) + x(3) - x(4) - 8;x(1)^2 + 2*x(2)^2 + x(3)^2 + 2*x(4)^2 - x(1) - x(4) - 10;2*x(1)^2 + x(2)^2 + x(3)^2 + 2*x(4)^2 - x(2) - x(4) - 5];
endobjfun = @(x)x(1)^2+x(2)^2+2*x(3)^2+x(4)^2-5*x(1)-5*x(2)-21*x(3)+7*x(4);
x0 = zeros(4,1); % 初值
xstat = ones(4,1); % 都是整数
[errmsg,objval,objX,t,c,fail] = BNB20_new(objfun,x0,xstat,[],[],[],[],[],[],@stBNB_fun1)objfun = @(x)5*x(4)+6*x(5)+8*x(6)+10*x(1)-7*x(3) - 18*log(x(2)+1)-19.2*log(x(1)-x(2)+1)+10;
x0 = zeros(6,1);
xstat = [0 0 0 1 1 1]';
lb = [0 0 0 0 0 0]';
ub = [2 2 1 1 1 1]';
A = [-1 1 0 0 0 0;0 1 0 -2 0 0;1 -1 0 0 -2 0;0 0 0 1 1 0];
b = [0 0 0 1]';
Aeq = [];
beq = [];
[errmsg,objval,objX,t,c,fail] = BNB20_new(objfun,x0,xstat,lb,ub,A,b,Aeq,beq,@stBNB_fun2)四、有约束非线性规划
nonlcon: nonlinear condition
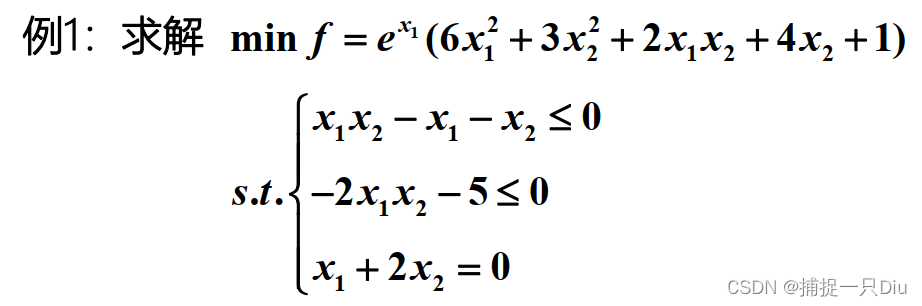
x0 = [-1;0.5];
Aeq = [1,2];
beq = [0];
options = optimoptions('fmincon','Display','iter','Algorithm','interior-point');
[x,fval,exitflag,output,lambda,grad,hessian] = fmincon(@objfmincon_1,x0,[],[],Aeq,beq,[],[],@nlincon_fun1,options)

d = [640,850,530,72]; % 目标距离
Ao = (d/2 + d/4 + 200); %飞机携带A炸弹分别摧毁4个目标所需要的油量
Bo = (d/3 + d/4 + 200); %飞机携带B炸弹分别摧毁4个目标所需要的油量
D = [Ao;Bo];
D = D(:)'; % 第一个约束条件的系数行向量
objfun = @(x)(1-0.65)^x(1)*(1-0.76)^x(2)*(1-0.50)^x(3)*(1-0.70)^x(4)*...(1-0.56)^x(5)*(1-0.72)^x(6)*(1-0.68)^x(7)*(1-0.66)^x(8);
x0 = zeros(8,1);
A = [D;1 0 1 0 1 0 1 0;0 1 0 1 0 1 0 1;1 1 0 0 0 0 0 0; 0 0 1 1 0 0 0 0;0 0 0 0 1 1 0 0;0 0 0 0 0 0 1 1;-1 -1 0 0 0 0 0 0; 0 0 -1 -1 0 0 0 0;0 0 0 0 -1 -1 0 0;0 0 0 0 0 0 -1 -1];
b = [2700;4;4;2;2;2;2;-1;-1;-1;-1];
Aeq = [];
beq = [];
lb = zeros(8,1);
ub = [];
nonlcon = [];
options = optimoptions('fmincon','Algorithm','interior-point');
[x,fval,exitflag,output,lambda,grad] = fmincon(objfun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options);
x = reshape(x,2,4)
p = 1 - fval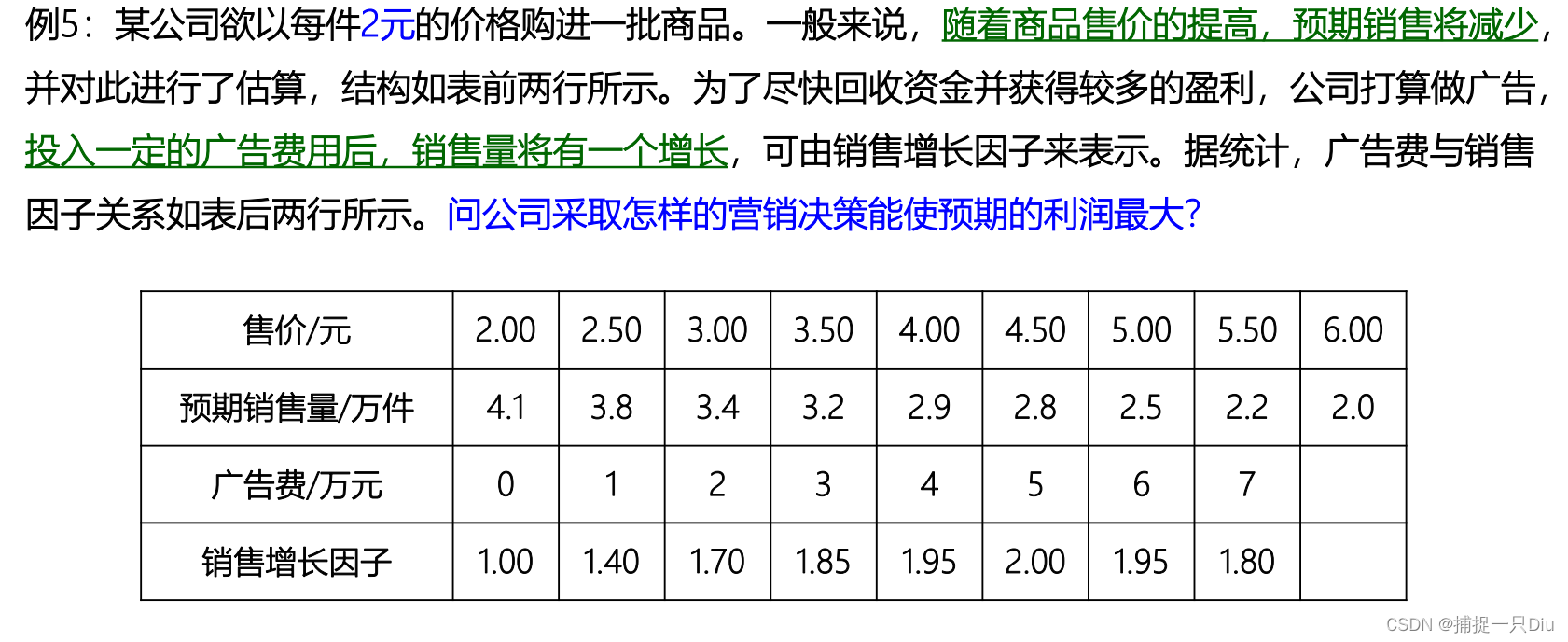
x = [2:0.5:6];
y = [4.1 3.8 3.4 3.2 2.9 2.8 2.5 2.2 2.0];
plot(x,y,'r-*')
grid on
title('售价与预期销售量散点图')
xlabel('售价')
ylabel('预期销售量')
% y = a*x + b
py = polyfit(x,y,1)z = [0:7];
k = [1 1.4 1.7 1.85 1.95 2 1.95 1.8];
figure
plot(z,k,'b-*')
grid on
title('广告费与销售增长因子散点图')
xlabel('广告费')
ylabel('销售增长因子')
% k = c*z^2 + d*z + e
pk = polyfit(z,k,2)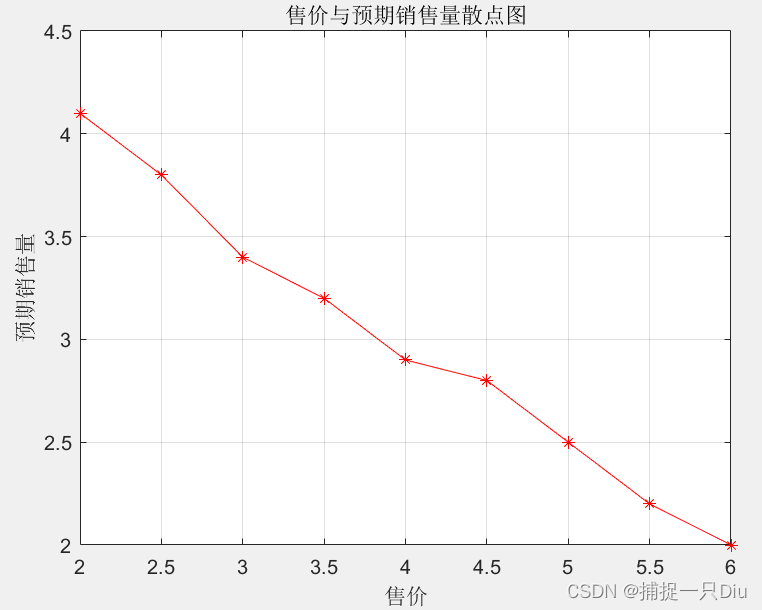

% x(1)-->x, x(2)-->z
objf = @(x)-((py(1)*x(1)+py(2))*(pk(1)*x(2)^2+pk(2)*x(2)+pk(3))*(x(1)-2)-x(2));
lb = [2;0];
x0 = [3;2];
options = optimoptions('fmincon','Algorithm','interior-point');
[x,fval,exitflag,output,lambda,grad] = fmincon(objf,x0,[],[],[],[],lb,[],[],options)五、半无限多元函数约束问题
fseminf
六、多目标规划问题



mobjf = @(x)[[36.9,35.8,24.9,29.9,45.8]*x;[-1,-1,-1,-1,-1]*x]; % 两个目标函数
x0 = ones(5,1);
goal = [1850,-55];
weight = [0.8,0.2];
A = [-1 -1 0 0 00 0 0 -1 -1];
b = [-23;-20];
Aeq = [];
beq = [];
lb = 8*ones(5,1);
[x,fval,attainfactor,exitflag,output,lambda] = fgoalattain(mobjf,x0,goal,weight,A,b,Aeq,beq,lb)
% attainfactor为达到因子,以实数形式返回。attainfactor 包含解处的 γ 值。
% 如果 attainfactor 为负,则目标过达到
% 如果 attainfactor 为正,则目标欠达到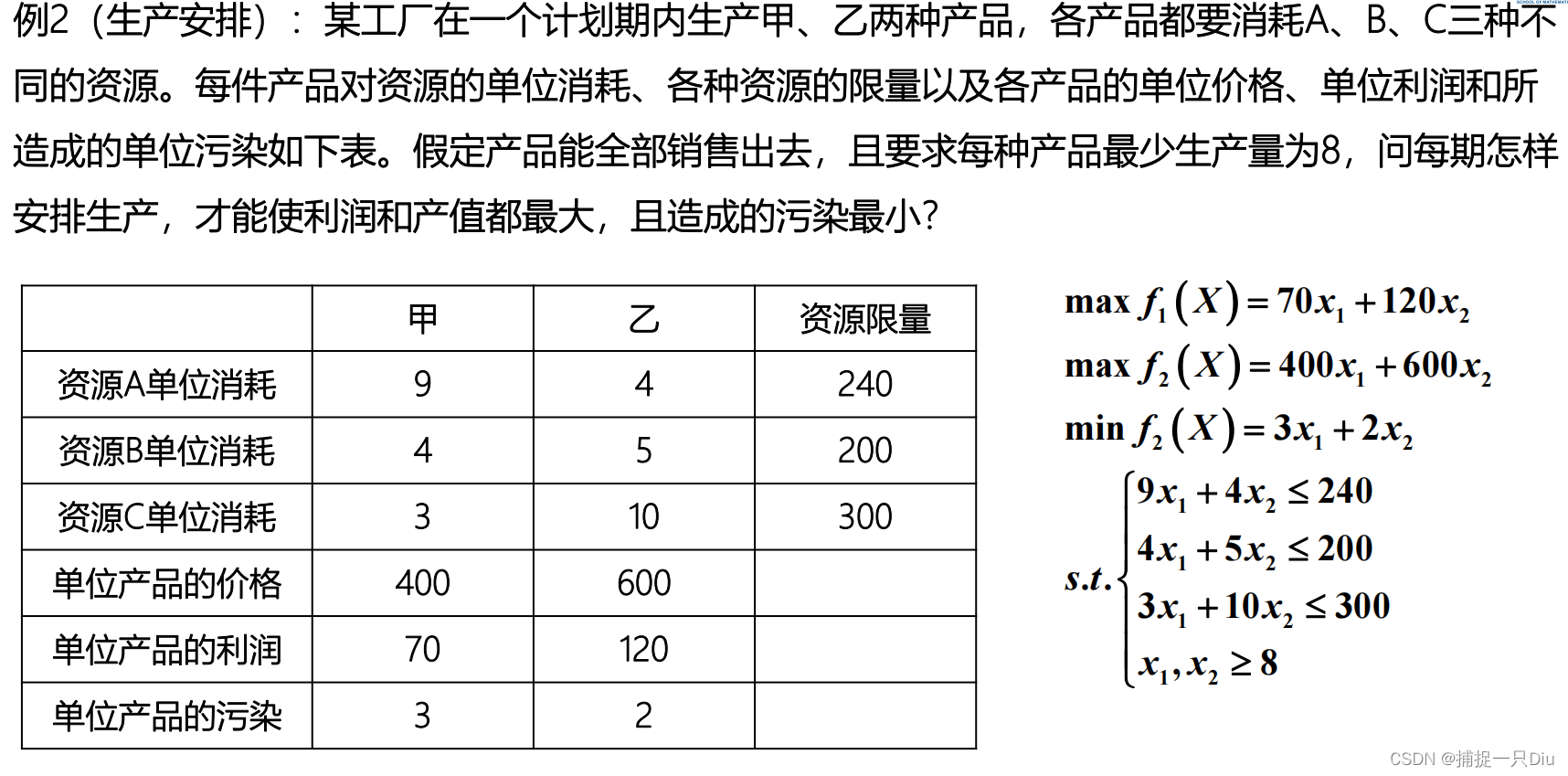
mobjf = @(x)[-[70 120]*x;-[400 600]*x;[3 2]*x];
x0 = ones(2,1);
goal = [-3900,-20000,80];
weight = [0.3 0.3 0.4];
A = [9 4;4 5;3 10];
b = [240;200;300];
lb = [8;8];
[x,fval,attainfactor,exitflag] = fgoalattain(mobjf,x0,goal,weight,A,b,[],[],lb)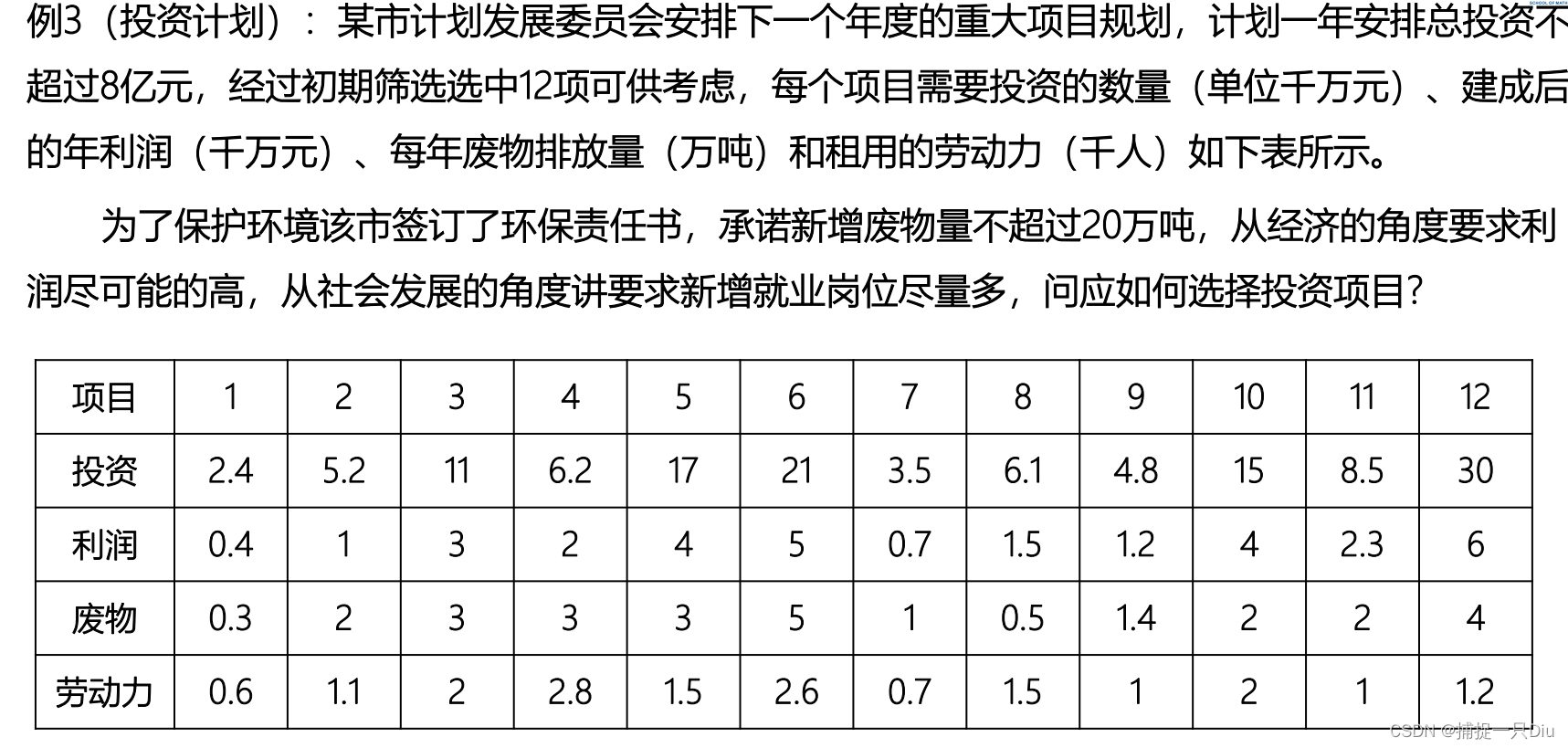

plan = xlsread('planning.xlsx',1,'B2:M5');
invest = plan(1,:); % 投资
profit = plan(2,:); % 利润
waste = plan(3,:); % 废物
labour = plan(4,:); % 劳动力
mobjf = @(x)-[profit*x;labour*x]; % 目标函数,最大值转化为最小值
x0 = zeros(12,1); % 初值选择
lb = zeros(12,1); % 决策变量下限
ub = ones(12,1); % 决策变量上限
goal = -[sum(profit);sum(labour)]; %目标
% goal = -[20.74;14.86]; % 通过线性规划求解在满足约束条件下的目标值
weight = abs(goal); % 权重
A = [invest;waste]; % 线性约束不等式系数矩阵
b = [80;20]; % 线性约束不等式右端向量
options = optimoptions('fgoalattain','Display','iter','MaxIterations',100,'ConstraintTolerance',1e-8);
[x,fval,attainfactor,exitflag,output,lambda] = fgoalattain(mobjf,x0,goal,weight,A,b,[],[],lb,ub,[],options)七、极小化极大问题



nonlcon: 定义非线性等式和不等式
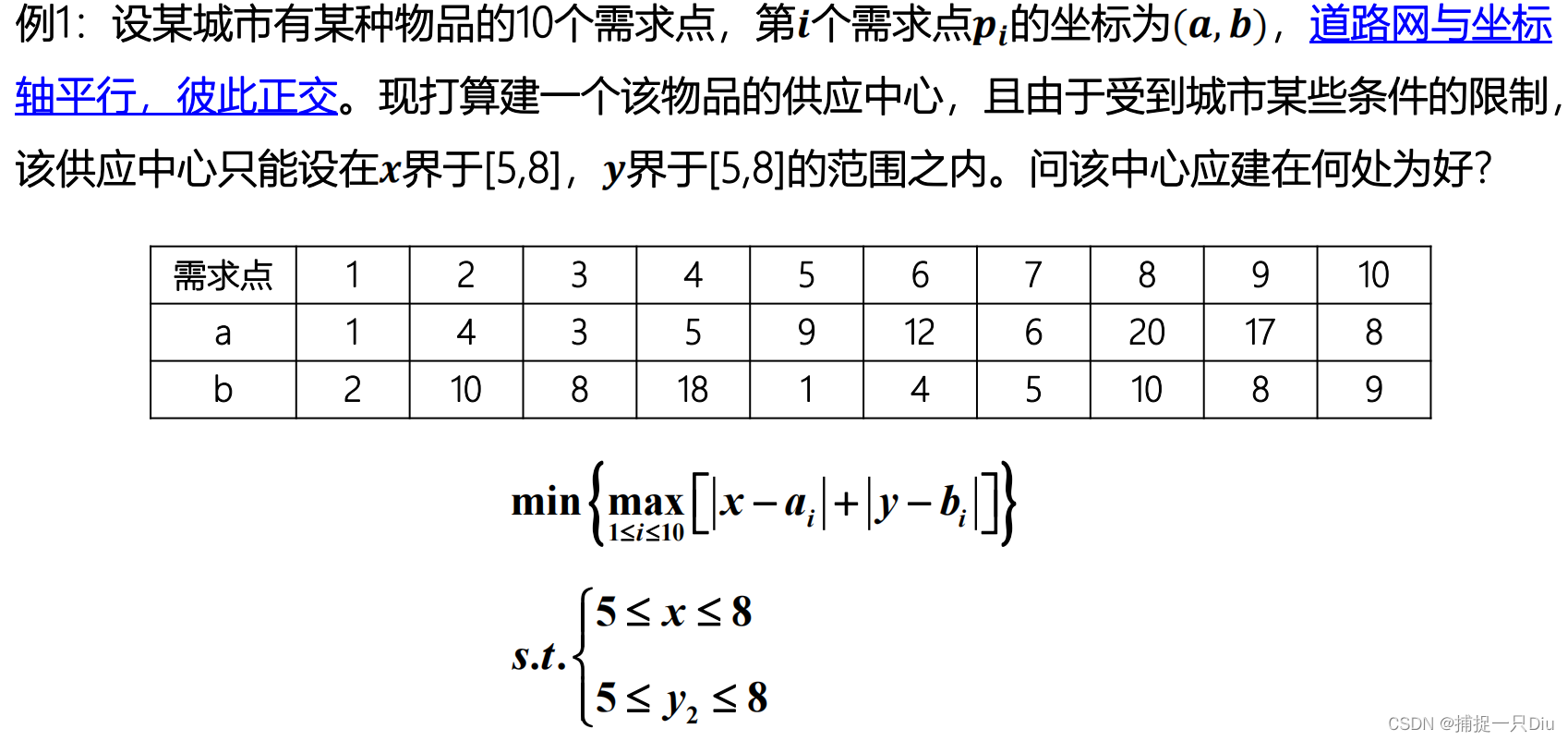
% Minimax一般是寻找一个局部最优解而不是全局最优解
lb = [5;5];
ub = [8;8];
x0 = [1;1];
[x,fval,maxfval,exitflag,output] = fminimax(@fminimax_fun1,x0,[],[],[],[],lb,ub)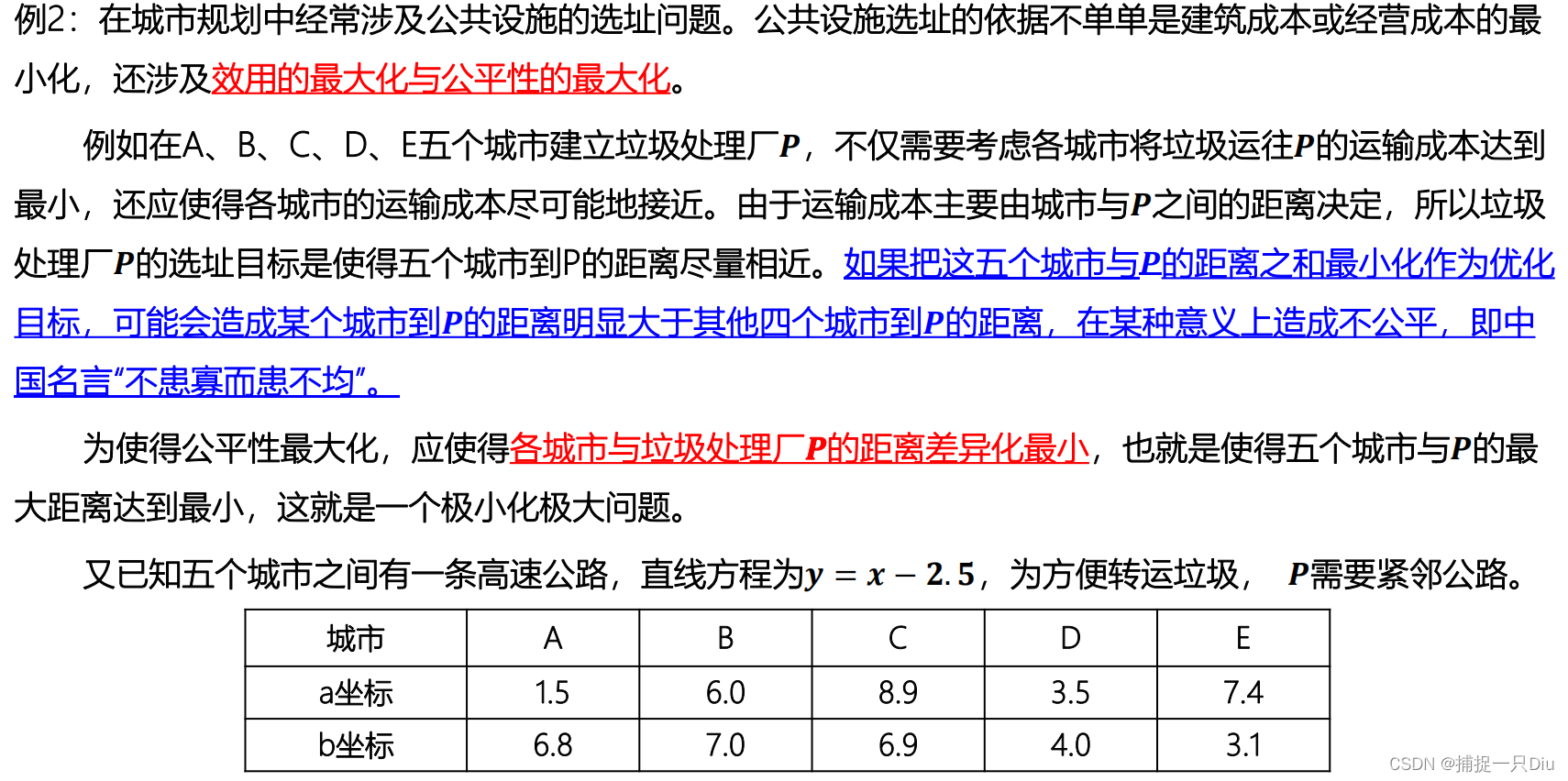

objf = @(x)sqrt([(x(1)-1.5)^2+(x(2)-6.8)^2;(x(1)-6.0)^2+(x(2)-7.0)^2; (x(1)-8.9)^2+(x(2)-6.9)^2;(x(1)-3.5)^2+(x(2)-4.0)^2; (x(1)-7.4)^2+(x(2)-3.1)^2]);
x0 = [0;0];
Aeq = [1 -1];
beq = [2.5];
[x,fval,maxfval,exitflag,output] = fminimax(objf,x0,[],[],Aeq,beq)八、线性约束最小二乘问题
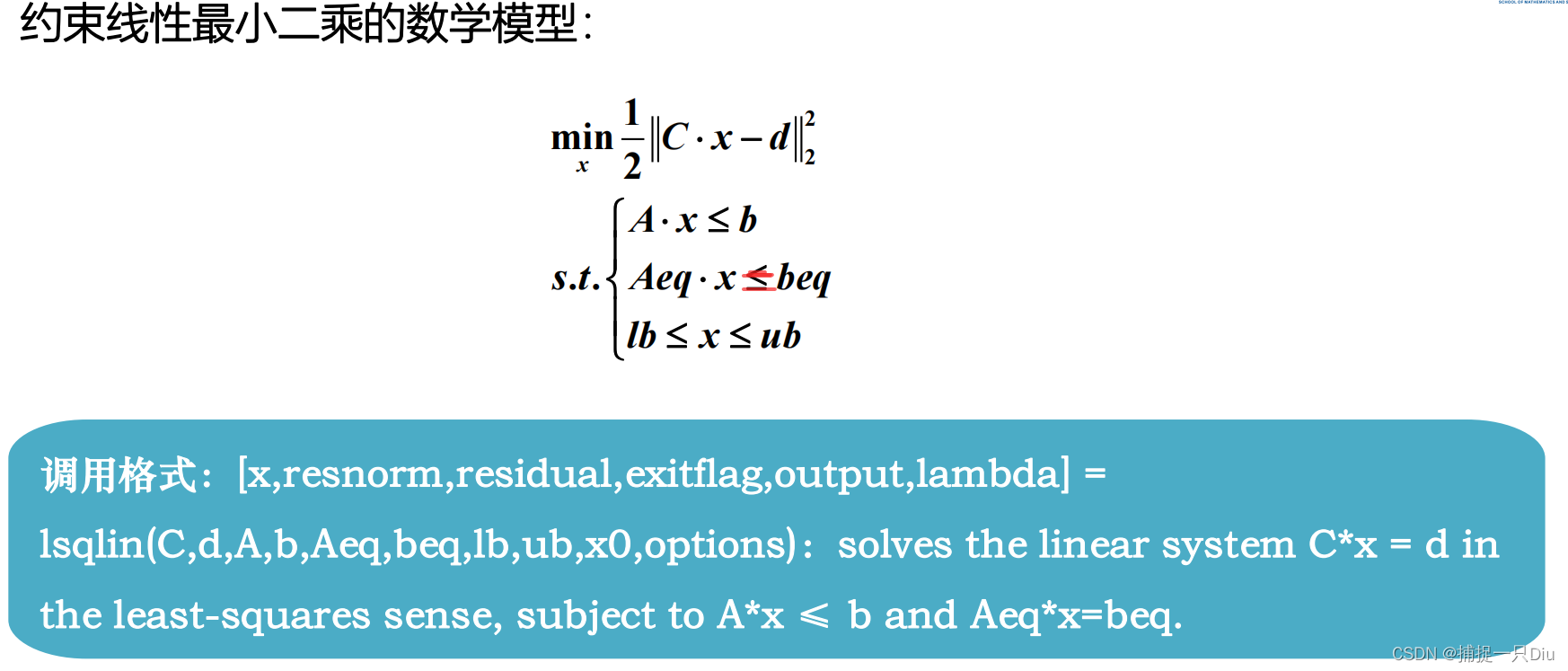
lsqlin: Solve constrained linear least-squares problems.

C = [0.9501 0.7620 0.6153 0.40570.2311 0.4564 0.7919 0.93540.6068 0.0185 0.9218 0.91690.4859 0.8214 0.7382 0.41020.8912 0.4447 0.1762 0.8936];
d = [0.0578 0.3528 0.8131 0.0098 0.1388]';
A = [0.2027 0.2721 0.7467 0.46590.1987 0.1988 0.4450 0.41860.6037 0.0152 0.9318 0.8462];
b = [0.5251 0.2026 0.6721]';
Aeq = [3 5 7 9];
beq = 4;
lb = -0.1*ones(4,1);
ub = 2*ones(4,1);
x0 = rand(4,1);
options = optimoptions('lsqlin','Algorithm','interior-point','Display','iter');
[x,resnorm,residual,exitflag,output,lambda] = lsqlin(C,d,A,b,Aeq,beq,lb,ub,x0,options)九、动态规划
dynprog
十、智能优化算法
1、遗传算法
nonlcon: 定义非线性等式与不等式
fh = @(x)-(x.*sin(10*pi*x) + 2);
fplot(fh,[-1,2])
% fmincon
v = [];
xi = [-1:0.8:1.5,1.5:0.1:2];
for x0 = xisolx = fmincon(fh,x0,[],[],[],[],-1,2);v = [v;x0,solx,-fh(solx)];
end
options = optimoptions('ga','Display','iter');
[x,fval] = ga(fh,1,[],[],[],[],-1,2,[],options)
fmin = @(x)5*x(4)+6*x(5)+8*x(6)+10*x(1)-7*x(3)-18*log(x(2)+1)-19.2*log(x(1)-x(2)+1)+10;
nvars = 6; % 决策变量的个数
intcon = [4,5,6]; % 取整决策变量下标
ub = [2 2 1 1 1 1]';
lb = [0 0 0 0 0 0]';
A = [-1 1 0 0 0 0;0 1 0 -2 0 0;1 -1 0 0 -2 0;0 0 0 1 1 0];
b = [0 0 0 1]';
options = optimoptions('ga','Display','iter');
[x,fval] = ga(fmin,nvars,A,b,[],[],lb,ub,@gacon_fun1,intcon,options)% 使用三中的BNB20_new函数
objfun = @(x)5*x(4)+6*x(5)+8*x(6)+10*x(1)-7*x(3)-18*log(x(2)+1)-19.2*log(x(1)-x(2)+1)+10;
x0 = zeros(6,1); % 初值
xstat = [0 0 0 1 1 1]'; % 都不是整数
xlb = [0 0 0 0 0 0]';
xub = [2 2 1 1 1 1]';
A = [-1 1 0 0 0 0;0 1 0 -2 0 0;1 -1 0 0 -2 0;0 0 0 1 1 0];
b = [0 0 0 1]';
Aeq = [];
beq = [];
[errmsg,objval,objX,t,c,fail] = BNB20_new(objfun,x0,xstat,xlb,xub,A,b,Aeq,beq,@gacon_fun1)2、粒子群算法

![]()
fh = @(x)-x.*sin(10*pi*x) - 2;
[x,fval,exitflag,output] = particleswarm(fh,1,-1,2)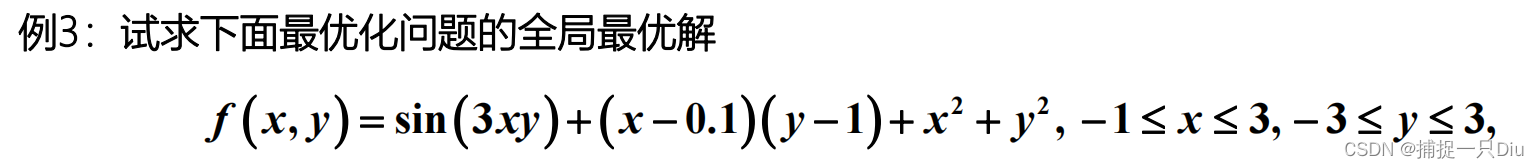
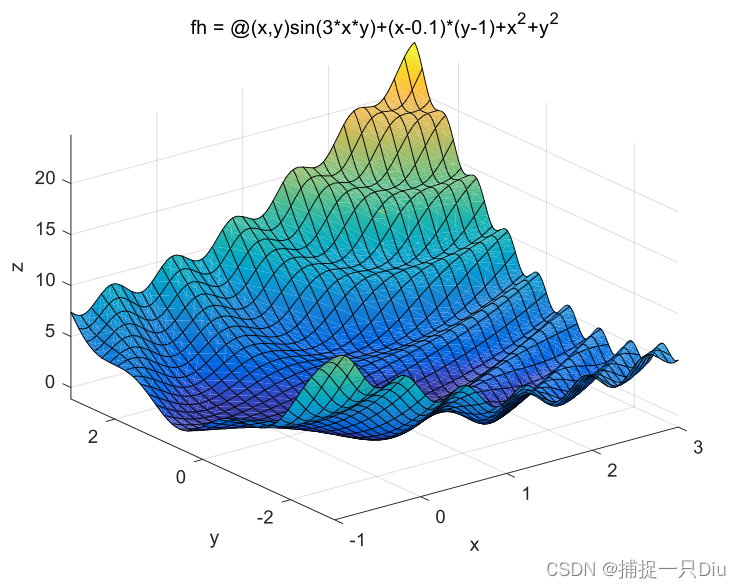
% fh = @(x,y)sin(3*x.*y)+(x-0.1).*(y-1)+x.^2+y.^2;
% fsurf(fh,[-1,3,-3,3])
fh = @(x)sin(3*x(1).*x(2))+(x(1)-0.1).*(x(2)-1)+x(1).^2+x(2).^2;
[x,fval,exitflag,output] = particleswarm(fh,2,[-1;-3],[3;3])3、模拟退火算法
% 测试函数函数dejong5fcn
[x,fval] = simulannealbnd(@dejong5fcn,rand(1,2))![]()
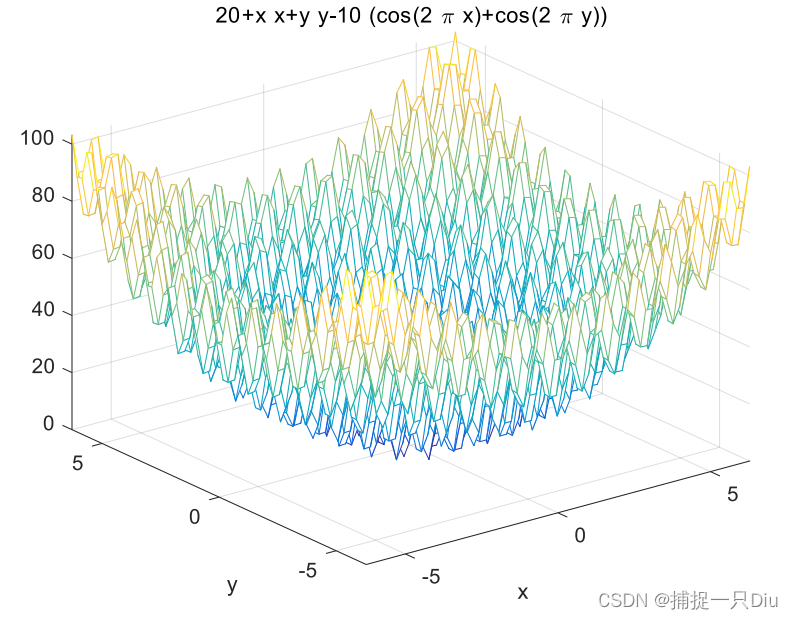
% fh = @(x,y)(20 + x^2 + y^2 - 10*(cos(2*pi*x) + cos(2*pi*y)));
% fsurf(fh)
fh = @(x)(20 + x(1).^2 + x(2).^2 - 10*(cos(2*pi*x(1)) + cos(2*pi*x(2))));
[x,fval,exitflag] = simulannealbnd(fh,rand(1,2))