AI很热,所以小伙伴们不免要温故知新旧时噩梦 - 线代。
(十几年前,还有一个逼着大家梦回课堂的风口,图形学。)
这个真的不是什么美好的回忆,且不说老师的口音,也不说教材的云山雾绕,单单是求解这件事情,你直接用python的numpy的lin-alg来做,它不香吗?
(matlab其实更好,还可以看动画,不过动辄几十个G,然后价格/破解也劝退,非专业选手装属实蛋疼,国内专业选手还在被禁止使用)
掰着手指头数一数,最烦的几种题型,其实都是可以一行搞定的 -
行列式计算 秩的计算 -
det = numpy.linalg.det(a)
rank = numpy.linalg.rank(a)向量点乘 叉乘 -
#内积 面积
muti_dot = numpy.dot(b, a)
#外积 法向量
muti_cross = numpy.cross(b, a)矩阵求逆 -
inv = numpy.inv(a)特征根与特征向量 -
x1,x2 = numpy.linalg.eig(a)
还免费附赠求解方程 -
x = numpy.linalg.solve(A, b)数学学习,最核心的是理解定义。最可惜的是教材上的所有重要的定义,几乎不是给正常地球人看的,不说是线性无关,至少也是驴唇不对马嘴。对于智商摸到天顶星的大神当然是无所谓,因为你把教材上的公式留下就够了,但是对于我等资质平庸者,那就是天坑,一见误终身那种。
拜托,一个工科生,学的目的不就是,3种分解拆吧拆吧,然后理解/优化算法?
#奇异值分解 对角阵
u,sigma,v = numpy.linalg.svd(A)#QR分解 正规正交阵-上三角阵
q,r = numpy.linalg.qr(A)#LU分解/Cholesky分解 下三角阵-上三角阵
l = numpy.linalg.cholesky(A)线代学习中,我认为最核心最提纲挈领的几个点 -
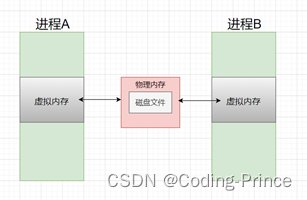
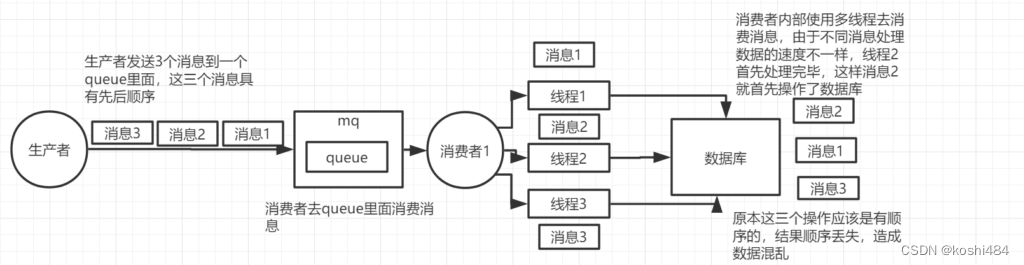
第一个,数组(行m),向量(列n),与矩阵(mxn)的关系,其实一个式子就够(矩阵和向量相乘,也就是我们常见的解方程组的样式) (借用神图)-

额,这个图目的不是,计算机可以用它来解方程了!当然,用计算机解方程这点也很重要。
画重点!线性变换的概念就是从这里面出来的。对于矩阵A,用一个n维的向量x乘它,就是对于这个矩阵本身的线性变换。也是从这里,线性代数被引入了工程。
第二个,矩阵分块和零矩阵。所有变换技巧的基础,就是适当分块,然后构造零子矩阵。各路大神们按照自己的需要和喜欢,整出了不同的分解方法,用来算相关性,推荐歌曲和商品,算pagerank,预测概率,等等等等等。比如,存入计算机的数据是稀疏矩阵,如果不把这些0踢出来,未经优化的数据直接参与运算,强如老黄的GPU,也得直接算的冒烟冒火吐了跪了。比如,不同的技巧对应不同的算法,同一个问题,算法的复杂度,区别天渊。
第三个,对角阵。这个是理解维数,坐标的基础,并且进一步可以扩张向量空间。
当然,对于科班生,每一个看似自然的定理,弄清背后的证明花的时间都远超前面这些。
统计是数据,图像是数据,海量的数据只能交给计算机,计算机理解相关性,唯一的方式就是靠矩阵(填格子得到)和线性代数。这也就从另一个方面说明了,IT的风口为啥总是要大家温书。假如十年后再来一个风口,大概率大家还是要一脑袋往线代上扎!
PS - 如果觉得不好,请告诉作者改进;如果觉得好,请推荐给你的小伙伴。