2015年认证杯SPSSPRO杯数学建模
A题 绳结
原题再现:
给绳索打结是人们在日常生活中常用的技能。对登山、航海、垂钓、野外生存等专门用途,结绳更是必不可少的技能之一。针对不同用途,有多种绳结的编制方法。最简单的绳结,有时称为单结,死结或反手结,英文称为Overhand Knot,是最常用的绳结之一,在各种复杂绳结中也是经常出现的基本元素。


这种结有一个特点,如果用于捆扎物体,由于无法彻底拉紧,所以很容易松脱,无法单独使用。但如果能够彻底拉紧,对较软和细的绳子而言,相当难以解开。所以用于捆扎物体时,可以连打两次单结,并将第二个结彻底拉紧,

这就构成一个难以自动松开的结。最常见的系鞋带方法,在本质上就是连打两次单结。为了便于解开,所以在打第二次结的时候需要把鞋带折成双股。
第二阶段问题:
1. 将第一阶段问题推广到其它打法的绳结。我们可以以系鞋带为例,原则上可以有多种打法来给鞋带打结。请你对尽量广泛的绳结打法进行总结,并给出一个较为简明的判别方法,来判断其在承受负荷时是否容易自动松脱。
2. 一根完整的绳子在两端受到拉力时,有一个被拉断的极限强度。在绳子中间打了一个结以后,由于绳结位置的弯折和缠绕,将使绳结位置成为整根绳子强度较低的一个薄弱点。请你建立合理的数学模型,通过研究不同绳结的打法来估计其强度。
整体求解过程概述(摘要)
绳索打结是人们在日常生活中的必要技能,在不同的情境中有不同的用处和编法,而绳结是否容易自动松脱的性质和对绳子极限强度的影响程度都是影响其使用的重要性能。打结的方式不同,对绳结的缠绕数,扭转数等空间特征和机械性能和造成了不同的影响。
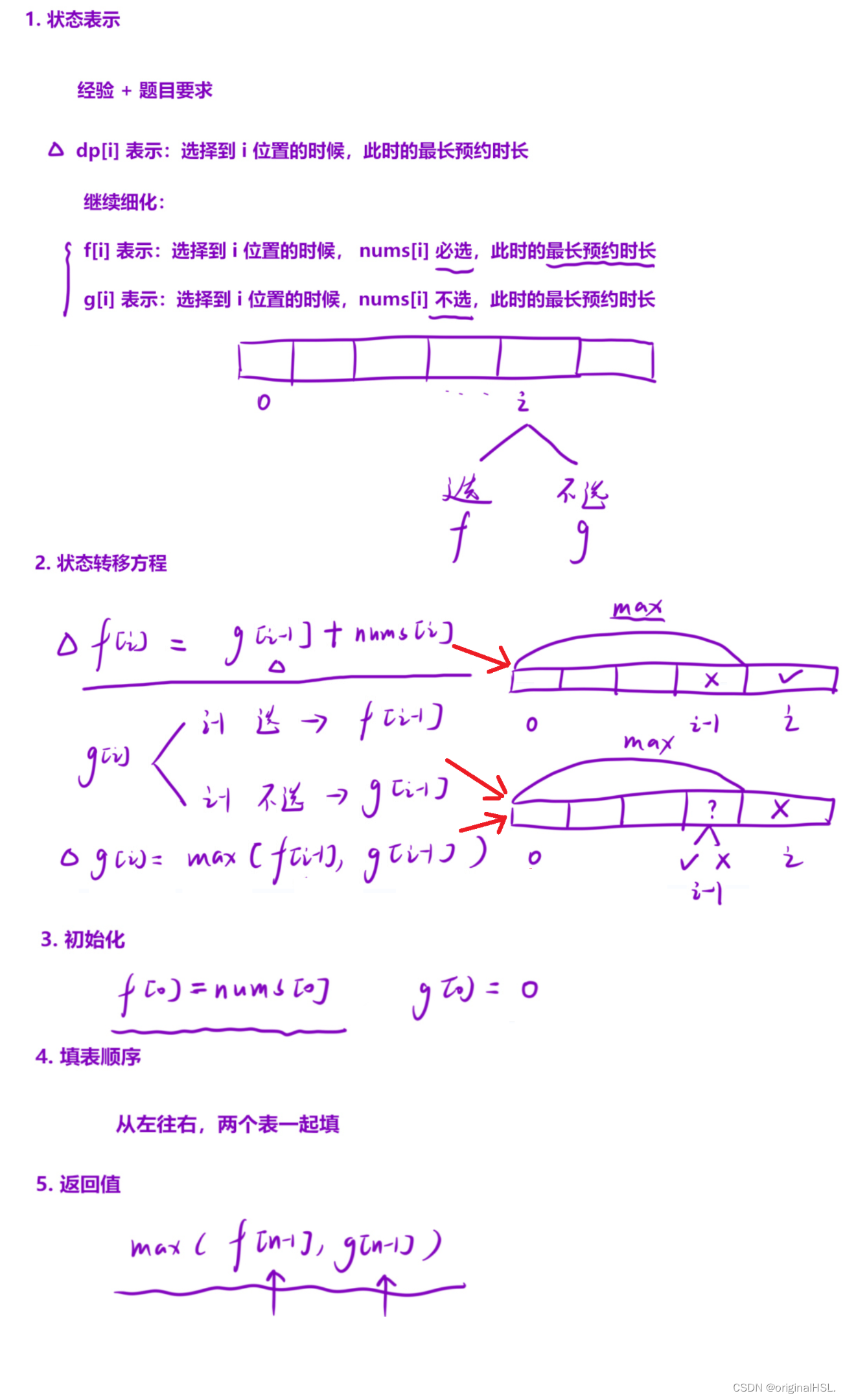
针对问题一:上一阶段,仅对由单结构成的同向结和镜像结的自动松脱性质进行了探究,本阶段要将自动松脱的性质进行推广。为了易于对绳结的空间特征进行描述,我们使用投影映射法、分类讨论的方法将空间上的点表示在平面上,分析不同打法下的单结在三维空间上的结点、交叉类型, 将它们投影到二维平面,写出它们对应的编码矩阵,建立绳结矩阵模型。分析数据的不同之处,找出变量,得出影响绳结稳定性的因素,结扣数、交叉点数、缠绕数。利用相关分析中的简单相关分析,用 Person 相关分析方法进行比较,利用 SPSS 软件,得到相关性 r 值,将这三种影响因素的 r 值进行比较,可得到结论。结扣数是与是否容易自动脱落之间的关系最密切的因素。从而得出判定每种绳结的结扣数,来比较每种绳结自动脱落性质的简单方法。
针对问题二:由于绳结的出现使绳子的极限强度发生了变化,所以我们以绳结对绳子的变化因素扭转程度和弯曲程度为变化量,通过实验,探究出变化量扭转数(扭转程度)和缠绕数(弯曲程度)对绳子极限强度的影响规律。然后我们用分类讨论的方法,讨论了不同材料下,扭转数和缠绕数对绳子极限强度影响程度问题,并对每个因素加权来刻画其影响程度。对于柔韧性材料,我们展开探究,建立了曲带模型,运用 EXCEL软件及物理定理得出扭转数和缠绕数对负荷率的关系。列举了不同打法的结来讨论,通过对每种结的扭转数和缠绕数的分析,来比较其负荷率,从而来估计其强度。
问题分析:
针对问题一,在第一阶段的研究中,我们仅仅对由单结两次不同打法的同向结和镜像结的松脱性质做了分析,在本阶段,我们要将绳结自动松脱的性质进行推广,对广泛的绳结进行总结。所以考虑将绳结用矩阵的方式表示,分析影响广泛绳结自动松脱性质的内在联系,找出影响其性质的主要因素。研究每个因素对其的影响规律,及哪个因素的影响大,从而得出可以简单直观判断绳结松脱性质的方法。
针对问题二,该问题主要研究的是绳结对绳子的极限强度的影响,考虑先从绳结对绳子的改变因素入手,控制单一变量,探究每种改变因素对绳子的极限强度的影响规律,建立曲带模型,来形象表述每种变量。最后探究不同打法的绳子,在变量的影响下,如何改变绳子的极限强度。
模型假设:
1. 假设材料的每一处都是均匀的。
2. 忽略绳子总长度的变化。
3. 假设在拉紧绳结的过程中,两头受力相同。
4. 假设每种打结方法每次打结时的相关参数不变。
5.曲带模型中打结长度理想化 L=1。
论文缩略图:

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:(代码和文档not free)
x2=[3,5,6,7,8,8,10,10]';
y=[16,26,31,36,40,41,51,50]';
x=[ones(8,1) x2];
plot(x2,y,'*')
[b,bint,r,rint,stats]=regress(y,x);
b,bint,stats,
rcoplot(r,rint)
z=b(1)+b(2)*x2;
plot(x2,y,'*',x2,z,'r')
程序2:不同结的绳子的极限强度模型的模拟的matlab程序
x=[1.0,1.2,1.6,1.9,2.1,2.3,2.4,2.5];
y=[175,177,182,185,187,189,190,192];
plot(x,y,'*');%y=a*x.^b
[a,b]=solve('177=a*1.2^b','189=a*2.3^b');
y1=173.7759*x.^0.1008;
plot(x,y,'*',x,y1,'-or');
R2=1-sum((y-y1).^2)/sum((y-mean(y)).^2)
%R2=0.9857
clc;
clear all
x=0:0.001:0.1;
y=(2000*x).*(x>=0&x<0.07)+140*(x>=0.07&x<0.09)+(-600000*x.^2+120000*x-5800).*(x>=0.09&x<=0.1);
plot(x,y,'r','linewidth',2)
axis([0 0.1 0 210])
grid on