上篇文章我们介绍了使用 无重复值 单调栈代码解决 含有重复值 的问题,在文章的最后,留下了一道考察相同思想的题目,今天我们来看看如何套路解决该题。
(还没看过前几篇介绍的小伙伴赶快关注,在 「单调栈」 集合里查看哦!)
力扣84.柱状图中最大矩形
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1 :
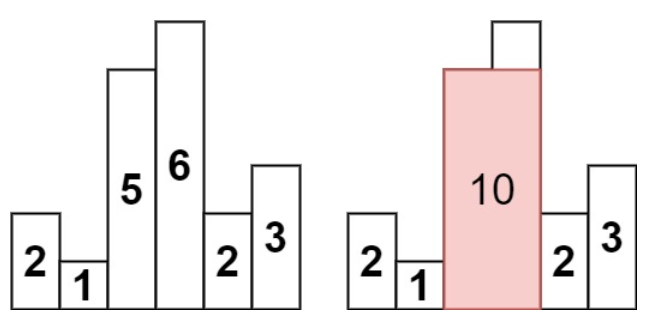
输入: heights = [2,1,5,6,2,3]
输出: 10
解释: 最大的矩形为图中红色区域,面积为 10
思路分析
学会了前几篇所介绍的单调栈思想之后,这道题目其实能够很轻松的想到解题方法,并且与 上一道题目 非常相似。
关键点: 寻找某个元素左右两侧最近的且比该元素小的数的区间。
如示例 1 中的元素 5 ,找到左右两侧的 1 和 2 ,所以有效的区间范围是下标为 1 的元素 1 和下标为4的元素 2 之间 的区间长度,可以用 下标之差 - 1 得到,4-1-1=2。
得到该区间后乘以该元素的大小即为最大矩形面积。
是不是很简单,接下来我们依旧思考一下需要考虑 处理重复值 的情况么?
根据 上一篇 总结的经验,只需考虑在含有相同值时,最后一个相同元素是否能够将答案计算正确呢?答案是可以的!
这里就不再赘述了,不太懂的小伙伴可以去查看上一篇文章哦 ~
代码
public static int largestRectangleArea1(int[] height) {if (height == null || height.length == 0) {return 0;}int maxArea = 0;Stack<Integer> stack = new Stack<Integer>();for (int i = 0; i < height.length; i++) {// 相等时也弹出while (!stack.isEmpty() && height[i] <= height[stack.peek()]) {int j = stack.pop();int k = stack.isEmpty() ? -1 : stack.peek();// 计算 面积 = 区间长度 * 该元素高int curArea = (i - k - 1) * height[j];maxArea = Math.max(maxArea, curArea);}stack.push(i);}while (!stack.isEmpty()) {int j = stack.pop();int k = stack.isEmpty() ? -1 : stack.peek();int curArea = (height.length - k - 1) * height[j];maxArea = Math.max(maxArea, curArea);}return maxArea;
}
代码解释
有了前两篇文章的铺垫,写出这道题的代码是不是轻而易举呢?
由于含有相同元素时,无需特殊处理,因此 while 判断中符号为 <=
。
计算最终面积时,区间的长度应为 i-k-1 ,注意下标计算别出错了哦~
~ 点赞 ~ 关注 ~ 星标 ~ 不迷路 ~!!!
关注回复「ACM紫书」获取 ACM 算法书籍~