深度解析KNN算法

KNN（K-最近邻）算法是机器学习中一种基本且广泛应用的算法，它的实现简单直观，应用范围广泛，从图像识别到推荐系统都有其身影。然而，随着数据量的增长，KNN算法面临着严峻的效率挑战。本文将深入讨论KNN算法及通过KD-Tree进行的优化方法。

KNN算法核心

KNN算法基于一个简单的假设：相似的事物更有可能靠近彼此。因此，通过观察一个实例最近的K个邻居来预测该实例的属性（分类或回归）。

实现步骤包括：

1. 距离度量：首先定义一个度量标准，以量化实例之间的“距离”。尽管欧氏距离是最常见的选择，但也可以根据具体问题选择其他度量方法。
2. 邻居的选择：对于给定的测试实例，计算并排序所有训练实例到该测试实例的距离，然后选择距离最近的K个实例作为其邻居。
3. 决策规则：在分类任务中，通常采用“多数投票”原则；在回归任务中，则可能计算K个邻居值的平均或加权平均。

尽管KNN在理论上简单有效，但它在实际应用中面临着计算效率和存储效率的双重挑战，特别是当数据集变得庞大和维度增加时。

KD-Tree：优化KNN查询

KD-Tree是一种用于组织和查询空间数据点的数据结构，尤其适用于维度相对较低的情况。通过将数据空间划分为较小的区域，KD-Tree能显著提高KNN查询的效率。

KD-Tree构建过程：

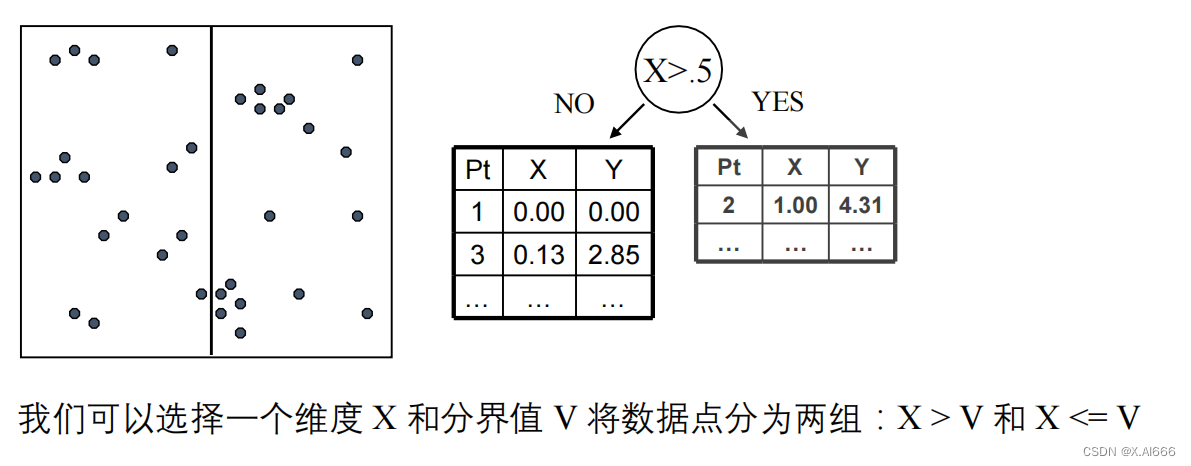
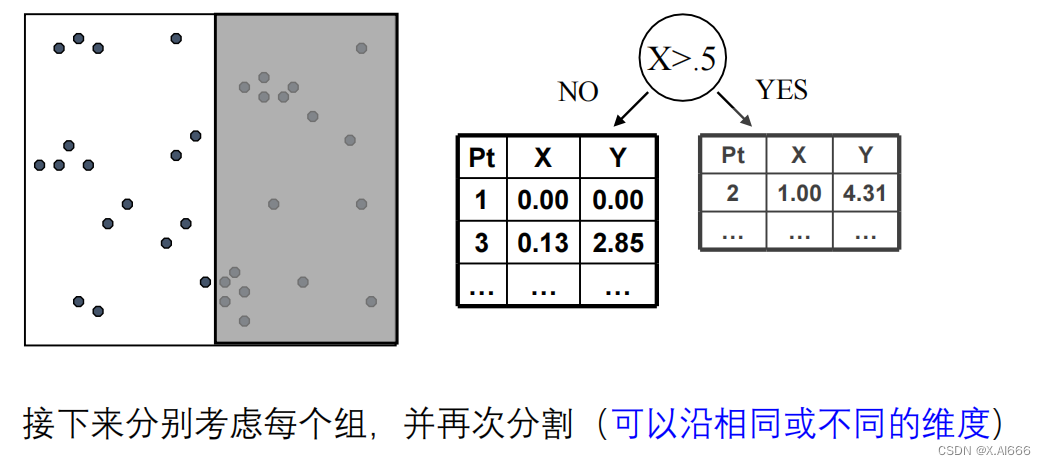
1. 选择轴：选择一个维度作为当前的划分轴，通常基于方差最大化或轮流选择维度。
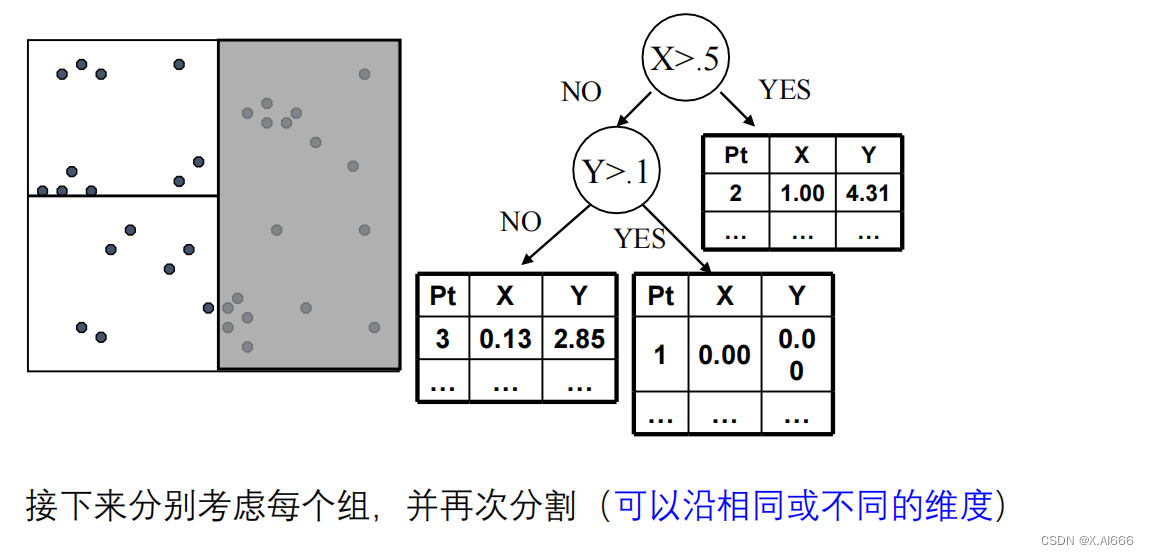
2. 分割数据：在所选轴上找到一个值作为分割点，将数据分为两部分，一部分的所有数据点在这个轴上的值都小于分割点，另一部分则相反。
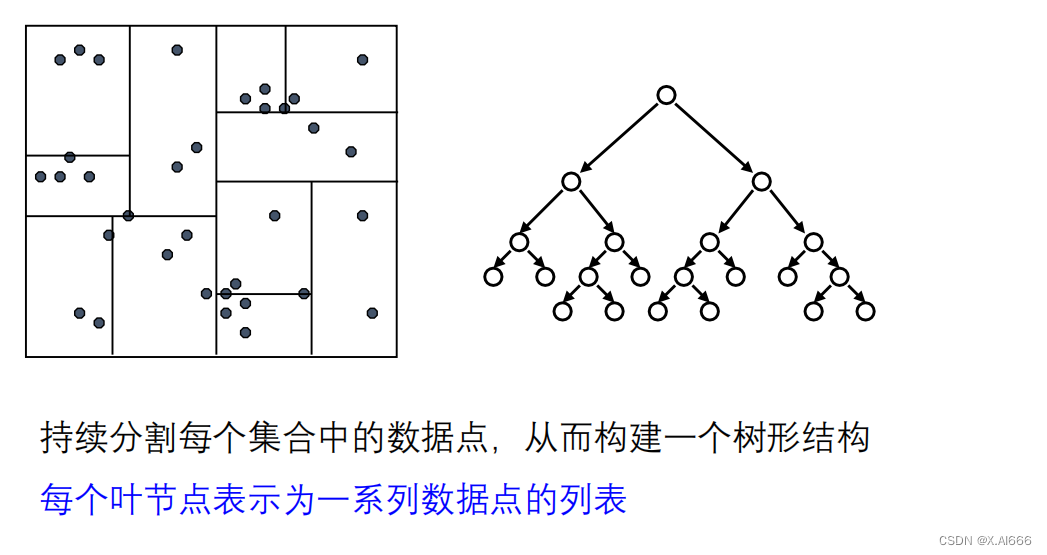
3. 递归划分：对分割产生的每个子集重复上述过程，直至满足某个停止条件，如子集大小下降到某个阈值以下。

KD-Tree查询过程：

1. 向下搜索：从根节点开始，递归向下搜索，直至达到叶节点。
2. 向上回溯：在向上回溯的过程中，检查另一侧的子树是否有更近的点，更新当前的最近点。
3. 剪枝优化：利用已找到的最近点距离作为半径画圆（或在高维情况下为球），与KD-Tree的节点区域进行比较，快速排除那些不可能包含更近点的区域。

通过KD-Tree，KNN查询的效率得到了显著提升，使其在处理大数据集时变得更加实用。

 在之前的讨论中，我们重点探讨了KNN算法的基础知识和通过KD-Tree优化查询效率的方法。然而，机器学习领域的研究和应用远不止于此。接下来，我们将深入探讨KNN算法的高级特性，包括距离加权近邻和局部加权回归，这些方法能够显著提高模型的预测性能。

距离加权KNN

传统的KNN算法在进行分类或回归时，通常给每个邻居同等权重。然而，在实际应用中，更靠近查询点的邻居应当对预测结果有更大的影响。这就引出了距离加权KNN的概念。

核心原理：

• 权重分配：给每个邻居分配一个权重，权重与邻居到查询点的距离成反比，例如使用距离的倒数作为权重。
• 加权决策：使用加权平均（回归问题）或加权投票（分类问题）来预测查询点的标签或值。

这种方法强调了邻居的“重要性”随距离增加而降低，有助于提高模型对局部数据分布的适应性。

局部加权回归

局部加权回归是一种灵活的非参数回归方法，它在每个查询点附近进行简单回归，为每个点提供定制化的拟合。这与KNN在本质上有所相似，因为它们都强调了局部邻居的作用。

实现步骤：

1. 选择核：定义一个核函数（如高斯核），用于计算查询点与训练实例之间的权重。
2. 局部回归：对每个查询点，根据其邻居的加权贡献，拟合一个回归模型（如线性回归）。
3. 预测：使用该局部回归模型来预测查询点的值。

局部加权回归特别适用于复杂的非线性数据集，能够提供更为精确和适应性强的预测。

懒惰学习与贪婪学习的比较

KNN算法和局部加权回归通常被归类为懒惰学习（Lazy Learning）方法，因为它们直到接收到查询请求时才开始真正的“学习”过程，即实时地从数据中学习。这与贪婪学习（Eager Learning）形成对比，后者在训练阶段就构建了一个全局模型。

懒惰学习的优势：

• 适应性：能够适应新数据，不需要重新训练模型。
• 精确度：对局部数据模式有很好的拟合能力。

贪婪学习的优势：

• 预测速度：一旦模型被训练，预测通常比懒惰学习方法快。
• 泛化能力：构建的全局模型可能更好地泛化到未见数据上。

总结

KNN算法及其衍生方法展示了基于实例的学习在机器学习领域的强大能力和灵活性。通过引入距离加权近邻和局部加权回归，我们可以进一步提升模型的性能，更好地捕获数据中的复杂模式。同时，对懒惰学习和贪婪学习的理解有助于我们根据具体问题选择最合适的学习策略。