编程实现黄金分割法、平分法和不精确一维搜索等最优化算法

在这里插入图片描述
解：
1、黄金分割法
思想：
黄金分割法是通过不断缩短搜索区间的长度来寻求一维函数的极小点，这种方法的基本原理是：在搜索区间[a,b]内按如下规则对称地取两点a1和a2
a1=a+0.382(b-a); a2=a+0.618(b-a);

黄金分割法的搜索过程是：
1）给出初始搜索区间 [a , b] 及收敛精度 eps ，将 λ赋以0.618
2）计算a1 和 a2，并计算起对应的函数值 f(a1),f(a2); ，
3）根据期间消去法原理缩短搜索区间，为了能用原来的坐标点计算公式，需进行区间名城的代换，并在保留区间中计算一个新的试验点及其函数值。
4）检查区间是否缩短到足够小和函数值收敛到足够近，如果条件不满足则返回到步骤2。
5）如果条件满足，则取最后两试验点的平均值作为极小点的数值近似解。

黄金分割法的流程图
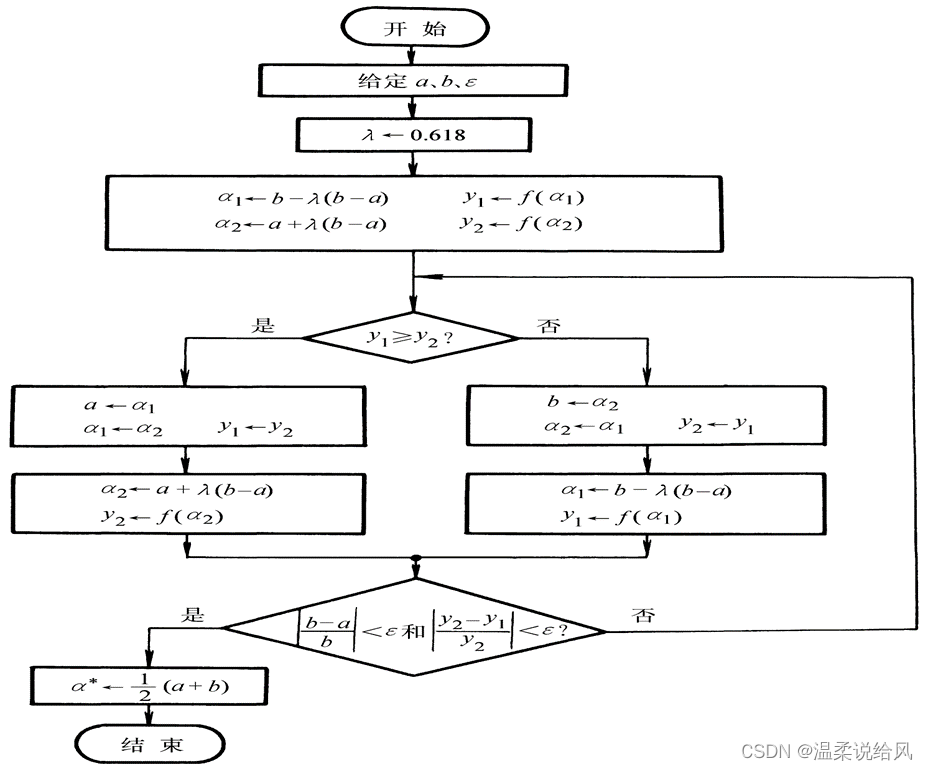
在这里插入图片描述

以f（x）= xx-5x+2 为例，
源程序如下：

#include<iostream>
using namespace std;
const float EPS=0.000001;//定义常量
float f(float);//定义函数f
float f(float x){return  x*x-5*x+2;
}int main()
{float a,b,x1,x2,f1,f2,t,eps;cout<<"a=";cin>>a;cout<<"b=";cin>>b;cout<<"eps=";cin>>eps;x1=a+0.382*(b-a);x2=a+0.618*(b-a);f1=f(x1);f2=f(x2);while (b-a>eps)//搜索精度循环节{t=f1-f2;if (t>EPS) {a=x1;x1=x2;f1=f2;x2=a+0.618*(b-a);f2=f(x2);}else if (t>=-EPS && t<=EPS) {a=x1;b=x2;x1=a+0.382*(b-a);x2=a+0.618*(b-a);f1=f(x1);f2=f(x2);}//函数值相等,两边区间均舍去else {b=x2;x2=x1;f2=f1;x1=a+0.382*(b-a);f1=f(x1);}}cout<<"x*="<<(a+b)/2;return (a+b)/2;system ("pause");}

运行截图如下：
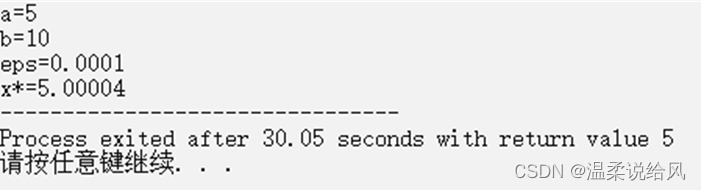
在这里插入图片描述

2、平分法
思想：
平分法要求函数f（x）在区间[a ,b]上为下单峰函数且具有连续的一阶导数。每迭代一次可去掉区间的二分之一。
设f（x）在区间[a ,b]上一阶导数连续，且f ’(a)<0,f’(b)>0。则取c=1/2（a + b），计算f ’©。
若f ’©=0,则c是极小值点；
若f ’©<0,则在[c ,b]内有极小点，保留区间[c ,b]；
若f ’©>0,则在[a ,c]内有极小点，保留区间[a ,c]。
把保留下来的区间仍记为[a ,b]，重复前面的过程，知道区间[a ,b]的长度充分小，满足所要求的精度为止。

其算法过程如下：
已知 a ，b 且 a <b ,f’(a)<0 ,f’(b)>0及e>0。

c=1/2(a + b)，转2。
若b-a≤e，则转4；否则转3。
计算f’©。若f’©=0,则转4；
若f’©<0,则令a=c，转1；
若f’©>0,则令b=c，转1。
令 x* =c。结束。
平分法的流程图

源程序如下：

#include<stdio.h>
#include<math.h>
//定义f(x)函数
double f(double x){return x*x+2*x+1;
}
//定义f(x)的导函数g(x)
double g(double x){double dx=0.001,dy,dd1,dd2;dy=f(x+dx)-f(x);dd1=dy/dx;Lab:dx=0.5*dx;//减小步长dy=f(x+dx)-f(x);dd2=dy/dx;//导数新值if(fabs(dd1-dd2)<1e-06) return dd2;else {dd1=dd2;goto Lab;};
}
int main() { double x0,f0,a=-1,b=2,c,d=0.001;int n;c=(a+b)/2;while(fabs(b-a)>d){//判断求导if(g(c)==0) n=0;else if(g(c)>0) n=1;else if(g(c)<0) n=2;switch(n) {case 0:break;case 1:b=c;c=(a+b)/2;break;case 2:a=c;c=(a+b)/2;break;}}x0=c;f0=f(c);printf("f(x)的最小值点在%f\n",x0);printf("f(x)的最小值为%f\n",f0);printf("%f",g(2));return 0;
}

在这里插入图片描述

3.不精确一维搜索
程序基本思想：

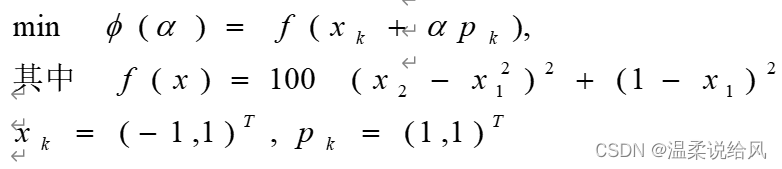
在这里插入图片描述

源程序如下：

#include <iostream.h>double f(double x1 , double x2)
{double result;result = 100 * (x2 - x1 * x1) * (x2 - x1 * x1) + (1 - x1) * (1 - x1);return result;
}
double g1(double x1 , double x2)
{double result;result = (-1) * 400 * (x2 - x1 * x1) * x1 - 2 * (1 - x1);return result;
}double g2(double x1 , double x2)
{double result;result = 200 * (x2 - x1 * x1);return result;
}double linesearch()
{double u, m, a, b, n, j ,best,min=0;double x1 , x2 ;u = 0.1 , m = 0.7;a = 0 , b = 999999999 ;n= 1 , j = 0 ;int flag=1;x1 = -1 , x2 = 1 ;while( flag){if( ( f(x1, x2) - f(n + x1, n + x2) + u*n*(g1(x1, x2) + g2(x1, x2)) ) < 0 && ( g1(x1 + n, x2 + n) + g2(x1 + n, x2 + n) - m*(g1(x1, x2) + g2(x1, x2))) >= 0 ){j = j + 1;cout<<j<<" " ;b = n;n = 0.5 * (a + n);flag=1;cout<<n<<" "<<f(n + x1, n + x2)<<endl;}if( ( f(x1, x2) - f(n + x1, n + x2) + u*n*(g1(x1, x2) + g2(x1, x2)) ) >= 0  && ( g1((x1 + n), (x2 + n)) + g2((x1 + n), (x2 + n)) - m*(g1(x1, x2) + g2(x1, x2))) < 0  ){j = j + 1;cout<<j<<" ";a = n;if( (2 * n - (a + b) * 0.5) > 0 ){n = (a + b) * 0.5;}else{n = 2 * n;}flag=1;cout<<n<<" "<<f(n + x1, n + x2)<<endl;}else if(( f(x1, x2) - f(n + x1, n + x2) + u*n*(g1(x1, x2) + g2(x1, x2)) ) >= 0  && ( g1((x1 + n), (x2 + n)) + g2((x1 + n), (x2 + n)) - m*(g1(x1, x2) + g2(x1, x2))) >=0 ){best = n;min=f(x1+best,x2+best);flag=0;cout<<"根据给定条件，不精确一维搜索的步长为:"<<best<<endl;}}return min;
}
int main()
{double bestresult;cout<<" 函数为Y = 100(x2-x1*x1)*(x2-x1*x1)+(1-x1)*(1-x1)"<<endl;bestresult=linesearch();cout<<"根据给定条件，不精确一维搜索后的最小值为："<<bestresult<<endl;}