1、什么是MD5

        计算机安全领域广泛使用的一种散列函数，是用以提供消息的完整性保护

2、MD5的优势

        （1）压缩性：任意长度的密码进过MD5加密后的长度是固定的

        （2）容易计算：从原数字计算到MD5很简单

        （3）抗修改性：修改任意一个数，MD5加密后的结果都天差地别

3、SpringBoot中使用MD5加密

（1）方法一：调用方法       推荐使用

        缺点：不能将解密

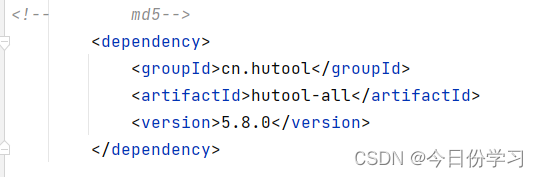
        1.导入依赖

        

        2.调用SecureUtil.md5()方法

        建议使用常量来提高安全性

        

（2）方法二：自定义加密        

        解密方法：一次是加密，两次是解密