树形结构 - 有向无环图
树是图的一种。
- 树形结构有一个根节点
- 树形结构没有回路
- 根节点:A
- 叶子节点:下边没有其他节点了
- 节点:既不是根节点,又不是叶子节点的普通节点
- 树的度:这棵树最多叉的节点有多少叉,这棵树的度就为多少
- 树的深度:最深有几层就是几
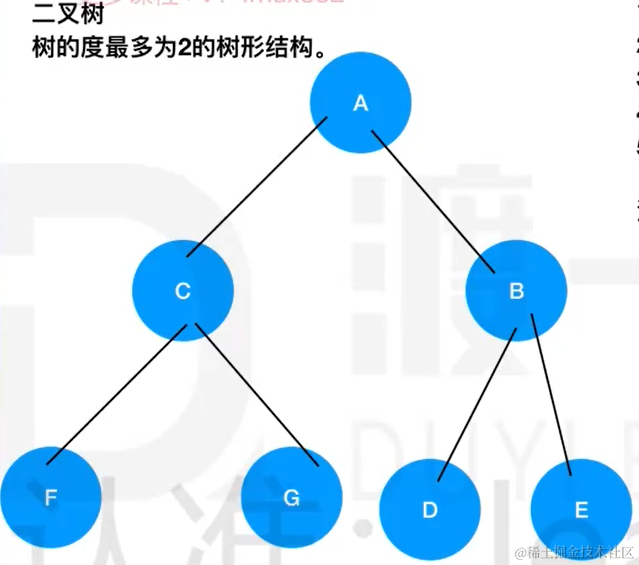
二叉树:
-
二叉树的根节点A
-
子节点:某个节点下面的节点
-
父节点:上级节点
-
叶子节点:CDE
-
节点:B
-
满二叉树:(1)所有的叶子节点都在最底层 (2)每个非叶子节点都有两个子节点
-
完全二叉树:
国内定义:(1)叶子节点都在最后一层或倒数第二层(2)叶子节点都向左聚拢
国际定义:(1)叶子节点都在最后一层或倒数第二层(2)如果有叶子节点,就必然有两个叶子节点
遍历二叉树
- 前序遍历:根左右
- 中序遍历:左根右
- 后序遍历:左右根
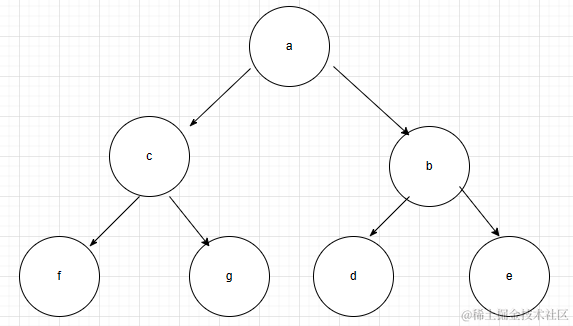
前序遍历
function Node(value) {this.value = valuethis.left = nullthis.right = null
}let a = new Node('a')
let b = new Node('b')
let c = new Node('c')
let d = new Node('d')
let e = new Node('e')
let f = new Node('f')
let g = new Node('g')
a.left = c
a.right = b
c.left = f
c.right = g
b.left = d
b.right = efunction preTraversal(root) {if (root == null) returnconsole.log(root.value)preTraversal(root.left)preTraversal(root.right)
}
preTraversal(a)
中序遍历
function Node(value) {this.value = valuethis.left = nullthis.right = null
}let a = new Node('a')
let b = new Node('b')
let c = new Node('c')
let d = new Node('d')
let e = new Node('e')
let f = new Node('f')
let g = new Node('g')
a.left = c
a.right = b
c.left = f
c.right = g
b.left = d
b.right = efunction inTraversal(root) {if (root == null) returninTraversal(root.left)console.log(root.value)inTraversal(root.right)
}
inTraversal(a)
后序遍历
function Node(value) {this.value = valuethis.left = nullthis.right = null
}let a = new Node('a')
let b = new Node('b')
let c = new Node('c')
let d = new Node('d')
let e = new Node('e')
let f = new Node('f')
let g = new Node('g')
a.left = c
a.right = b
c.left = f
c.right = g
b.left = d
b.right = efunction postTraversal(root) {if (root == null) returnpostTraversal(root.left)postTraversal(root.right)console.log(root.value)
}
postTraversal(a)
还原二叉树
给出前中序还原二叉树
let preTraverse = ['a', 'c', 'f', 'g', 'b', 'd', 'e'];
let inTraverse = ['f', 'c', 'g', 'a', 'd', 'b', 'e'];function Node(value) {this.value = valuethis.left = nullthis.right = null
}function binaryTree(preTraverse, inTraverse) {if (preTraverse == null || inTraverse == null || preTraverse.length == 0 || inTraverse.length == 0 || preTraverse.length != inTraverse.length) returnlet root = new Node(preTraverse[0])// 找到根节点在中序遍历中的位置let index = inTraverse.indexOf(root.value)// 先序序遍的左子树let preLeft = preTraverse.slice(1, 1 + index)// 先序遍历的右子树let preRight = preTraverse.slice(1 + index, preTraverse.length)// 中序遍历的左子树let inLeft = inTraverse.slice(0, index)// 中序遍历的右子树let inRight = inTraverse.slice(index + 1, inTraverse.length)root.left = binaryTree(preLeft, inLeft)root.right = binaryTree(preRight, inRight)return root
}let root = binaryTree(preTraverse, inTraverse)
console.log(root.left)
console.log(root.right)

给出中后序还原二叉树
let postTraverse = ['f', 'g', 'c', 'd', 'e', 'b', 'a'];
let inTraverse = ['f', 'c', 'g', 'a', 'd', 'b', 'e'];function Node(value) {this.value = valuethis.left = nullthis.right = null
}function binaryTree(postTraverse, inTraverse) {if (postTraverse == null || inTraverse == null || postTraverse.length == 0 || inTraverse.length == 0 || postTraverse.length != inTraverse.length) returnlet root = new Node(postTraverse[postTraverse.length - 1])// 找到根节点在中序遍历中的位置let index = inTraverse.indexOf(root.value)// 后序序遍的左子树let postLeft = postTraverse.slice(0, index)// 后序遍历的右子树let postRight = inTraverse.slice(index, postTraverse.length - 1)// 中序遍历的左子树let inLeft = inTraverse.slice(0, index)// 中序遍历的右子树let inRight = inTraverse.slice(index + 1, inTraverse.length)root.left = binaryTree(postLeft, inLeft)root.right = binaryTree(postRight, inRight)return root
}let root = binaryTree(postTraverse, inTraverse)
console.log(root.left)
console.log(root.right)