SharpContour: A Contour-based Boundary Refinement Approach for Efficient and Accurate Instance Segmentation

论文链接：[2203.13312] SharpContour: A Contour-based Boundary Refinement Approach for Efficient and Accurate Instance Segmentation (arxiv.org)

代码链接：无

1. 背景和动机

实例分割是计算机视觉中的一个重要任务，它旨在识别并分割图像中的每个目标实例。近年来，基于深度学习的实例分割方法取得了显著的进展，但是在边界区域的分割质量仍然不尽如人意，导致实例分割的准确性和鲁棒性受到限制。

为了提高边界区域的分割质量，近些年出现了一些边界细化的方案，本文指出一个好的边界细化方案应该需要满足以下三个基本要求：准确、高效以及通用。

然而目前效果最好的方案均无法同时满足以上三个要求：

• 准确、通用但不高效

  • [2104.05239] Look Closer to Segment Better: Boundary Patch Refinement for Instance Segmentation (arxiv.org)：BPR需要基于实例分割模型输出的Mask的边缘去提取大量Patch，并独立对各个Patch进行计算，这会带来比较大的计算成本。

  • [1912.02801] PolyTransform: Deep Polygon Transformer for Instance Segmentation (arxiv.org)：PolyTransform提出了第一个基于contour的边缘优化方案，它使用mask-based模型输出的Mask生成初始的contour，然后再通过Transformer网络对Contour进行Refine，Transformer网络会带来较大的计算量。

• 准确、高效但不通用（大都仅能对一些mask-based模型的输出进行Refine，无法应用于contour-based模型）

  • [1912.08193] PointRend: Image Segmentation as Rendering (arxiv.org)：PointRend仅在一些模糊边界点上进行分割，从而降低了计算量。
  • [2104.08569] RefineMask: Towards High-Quality Instance Segmentation with Fine-Grained Features (arxiv.org)：在上采样阶段通过引入细粒度的特征来进行整个目标的Refine。

• 高效、通用但不准确

  • 一些Regression-based contour evolution方案，例如Dance、DeepSnake等，虽然高效，但其对于角落、尖端等区域分割精度依然不佳。本文指出，这些基于回归的模型之所以效果不佳的原因在于：他们的回归方法需要平衡回归误差和当前轮廓的平滑度，并且在特征学习过程中相互高度依赖，这使得这些方案对于角落等尖端区域分割结果过于光滑。

由于Contour-Based方案天然具有高效和通用性，并且易于用于mask-based方案后（从Mask中提取Contour是很直接的）。因此，本文基于Contour提出了一种新的BoundaryRefine方案，名为SharpContour，其同时具有准确、高效以及通用的优点。SharpContour将一个Coarse Contour作为输入，并独立地对各个顶点进行变形，以达到Refine的效果。

• 为了避免由于“独立性”而带来的artifacts，本文限制了每个顶点的移动方向——法线方向，同时以循环的方式进行迭代，使得整个优化过程更加稳定。
• 为了平衡高效性和准确性，本文不是直接对顶点的offset进行回归，而是对一些离散的点进行分类，来决定最终的目标位置。具体的：
  • 在移动方向上采样一些点，并将这些点进行分类，分为inner和outer两类，以此来获取其flipping position（顶点在沿着移动方向移动到某个位置后状态发生反转的位置，具体见后文说明），用于确定边界。
  • 这里的分类器担任一个至关重要的角色，因此，本文进行了特殊设计——Instance-aware Point Classifier (IPC)：
    • IPC可以根据不同的InstanceBoundary去预测一个顶点的inner或outer的状态，并以一个概率分数的形式来表示
    • 为了提高准确性，IPC需要具有以下两个重要特征：
      • Instance Aware：对于同一点来说，针对不同的InstanceBoundary，其可能是具有不同的状态，因此，IPC需要对Instance有所感知，本文是通过基于各个实例动态生成IPC参数的方式来实现的。
      • Boundary Details：IPC需要能够捕获Boundary Details，因此，IPC的输入特征来自于高分辨率的细粒度特征。
    • 基于IPC的输出，便可以确定在优化过程中如何移动各个顶点：
      • 移动距离：通过目标的尺寸（可以根据CoarseMask大致确定）以及IPC输出的概率分数来共同决定。
      • 移动方向：按照前文所说，是通过inner、outer状态来确定。

2. 具体方案

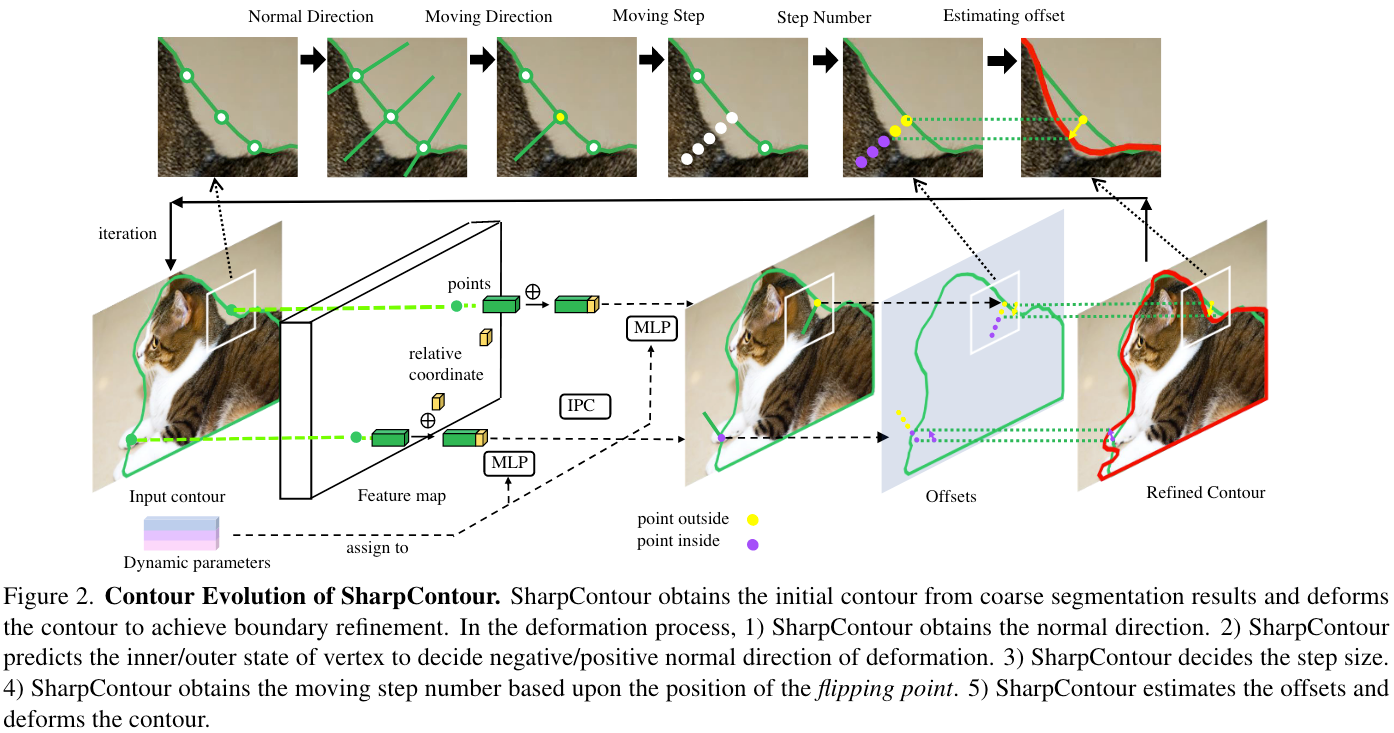
2.1 Contour Evolution

对于一个远离边缘的顶点$x_i$来说，在Evolution过程中的一次迭代可以表达为：
$$x_i^{\prime }=x_i+m{s}_i{d}_i$$
其中，$d_i$表示移动方向，$s_i$表示移动步长，$m$则是步数。

• 移动方向

对于每一个顶点$x_i$，IPC $\phi \left(x_i\right)$会输出一个范围为$[0,1]$的标量，用于指示该顶点是位于outside（例如$\phi \left(x_i\right)=1$）还是inside（例如$\phi \left(x_i\right)=0$），如果$\phi \left(x_i\right)=0.5$ 则说明IPC不确定这个点是outside还是inside，则说明该点可能位于Boundary上。关于IPC的具体细节，在2.2节详述。

• 移动步长

移动步长的确定来自于两个方面：object size（BBox的面积，记为$A$）以及IPC对于该顶点的不确定程度。当Object比较大的时候，步长应该也大一点，而如果IPC对于该订单的不确定性比较高，那么步长应该小一点。

具体而言，步长$s_i$定义如下：
$$s_i=\lambda \sqrt{A}\left|\phi \left(x_i\right)-0.5\right|$$
其中$\lambda$是一个经验系数，实验中设定为0.003，$\left|\phi \left(x_i\right)-0.5\right|$ 则衡量的是IPC对于$x_i$的不确定性。

• 步数

理想中，希望顶点会渐进地移向准确的目标边界，因此，本文会沿着移动方向step-by-step地移动顶点，并且在每次移动后都重新使用IPC去检验该顶点的新状态。

当某次移动后，该顶点的状态发生了反转，那么本文将这个顶点所在的位置定义为flipping point，从原位置移动到该flipping point所需要的移动次数即为移动步数$m$。为了避免顶点朝着一个不合适的方向移动太远，本文还为移动步数$m$设定了一个上限$M$。

Iteratively Evolution

对于一个初始的Contour C ( 0 ) : { x i ∣ i = 1 , … , N } C^{(0)}: {\left\{x_i \mid i=1, \ldots, N\right\}} C(0):{xi​∣i=1,…,N}，会首先进行一次上述的迭代过程以获得一个更新后的Contour $C^{(1)}$。然后本文会继续迭代进行另一轮迭代，得到新的Contour$C^{(2)}$，最终经过多轮迭代后，得到一系列Contour $\left\{C^{(0)},C^{(1)},\dots ,C^{(n)},\dots \right\}$。

需要注意的是，在某轮迭代中，一旦某个顶点到达了flipping point，这意味着该顶点到达了边界，此时其不再参与后续迭代，这提升了SharpContour的效率。

2.2 Instance-aware Point Classifier

Instance-aware Point Classifier (IPC) $\phi$ 作用是：给定一个顶点$x_i$，预测其状态，用于指示其对于准确的目标边界的相对位置。

IPC：

• 输入：$x_i$的细粒度特征及其对于对应BBox的相对位置

• 输出：$x_i$位于目标外部或内部的概率

• 参数：IPC的参数会根据每个实例动态预测，使得IPC Instance-Aware。

Fine-grained Feature

为了使得IPC可以区分细节，本文将来自于Instance Segmentation Backbone的高分辨率的细粒度特征作为IPC的输入。为了降低计算量，同时进一步对特征进行降维、编码，还会使用一个卷积层对细粒度特征进行进一步处理。记顶点$x_i$对应的编码后的特征为$f_i$。

为了提升IPC对于位置的感知能力，本文还会将$x_i$相对于其Instance BBox的位置坐标$c_i$作为额外特征，与$f_i$拼接起来，得到一个新的细粒度并且具有位置感知能力的特征向量$f_i^c=\left[f_i;c_i\right]$。$f_i^c$即为IPC的输入。

Instance-aware Dynamic Parameters

正如前文所说，IPC需要具有实例感知的能力，因为对于不同实例来说，同一个点的状态可能是不一样的。

受启发于[2003.05664] Conditional Convolutions for Instance Segmentation (arxiv.org)，本文会根据每个实例的特征动态预测每个实例的IPC $\phi$的参数 $\theta$。

例如对于Mask R-CNN来说，本文参考CondInst设计了一个Boundary Controller Head用于为每个实例动态获取其参数。

Boundary Controller Head是一个非常紧凑和轻量级的网络，具有三个全连接层，其最终输出维度与IPC参数数目相同，通过共享Mask R-CNN Mask Head的特征，IPC所需要的额外计算量很少。最终IPC可以被写为以下式子：
$$\phi \left(x_i\right)={\phi }_{\theta }\left(\left[f_i,c_i\right]\right)$$
IPC输出的含义：

• $\phi \left(x_i\right)>0.5$：$x_i$被认为是位于目标外侧，则预测label ${\hat{y}}_i=1$

• $\phi \left(x_i\right)<=0.5$：$x_i$被认为是位于目标内侧，则预测label ${\hat{y}}_i=0$

IPC的实现比较简单， 由三个带有ReLU激活函数的MLP构成，最后接一个Sigmoid函数用于输出概率。

PS. 我理解的是：Boundary Controller Head的三个全连接层各自输出IPC中的三个MLP的参数，以实现动态参数。由于没有源码不确定具体方式。

2.3 Training Strategy and Loss Function

Training Strategy

• 训练阶段：SharpContour通过随机抽取真实实例边界附近的像素来训练BoundaryControllerHead，以生成IPC的参数。

• 推理阶段：SharpContour 从粗分割结果中得到初始轮廓，然后进行Contour Evolution Process，以迭代完成Refine操作。

Loss Function

SharpContour使用FocalLoss去训练BoundaryControllerHead（用于生成IPC三个MLP的参数）以及编码细粒度特征的一层Conv。

由于训练时，positive和negative points之间的比例是不一定的，因此，这里添加了一个额外的动态系数$\alpha$进行平衡，$\alpha$是当前batch采样点中positive和negative points之间的比例。

最终IPC训练Loss Function如下：
$$L_{IPC}=\{\begin{array}{r}-\alpha {\left(1-{\hat{y}}_i\right)}^{\gamma }\log \left({\hat{y}}_i\right),y_i=1\\ -(1-\alpha ){\left({\hat{y}}_i\right)}^{\gamma }\log \left(1-{\hat{y}}_i\right),y_i=0\end{array}$$
其中$\hat{y}$为预测的label，$\gamma$为FocalLoss中的difficulty factor，本文在实验中设置为2。

再结合上Instance Segmentation Model进行联合训练，整体Loss如下：
$$L=L_s+\mu L_{IPC}$$
其中$L_s$是原Instance Segmentation Model的Loss，$\mu$在实验中被设置为10。

3.实验结果

3.1 Comparisons with the state-of-the-art

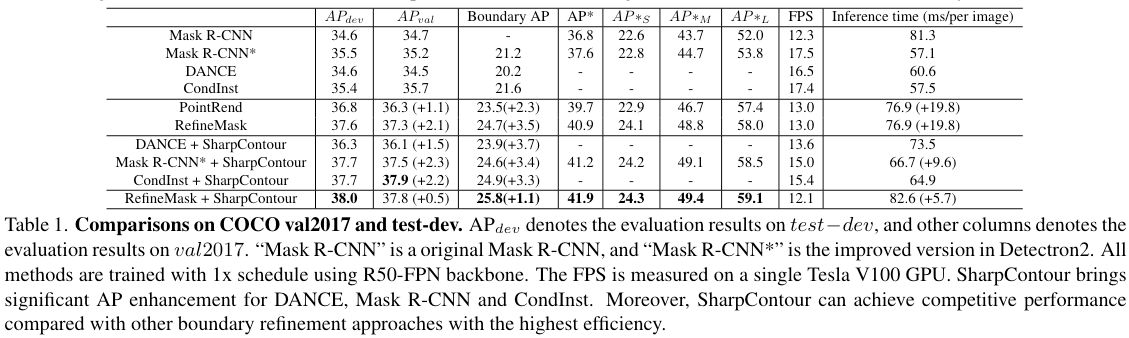
从实验结果来看，SharpContour策略效果还是不错的，整体增加的overhead也比较小。

Qualitative Comparison

3.2 Ablation Study

Training Schema

Training Alone表示固定InstanceSegmentationModel的参数，仅训练BoundaryControllerHead和Encoding Feature的Conv Layer，而Joint Training代表还同时训练InstanceSegmentationModel。

可以看出，联合训练的效果明显更好。

Effects of dynamic step size

动态步长效果更好，并且训练更稳定。

Regression-based Baselines

相较于使用离散的分类策略，本文也尝试了两种回归方案：

• Reg.1：回归offset vectors
• Reg.2：回归沿着法线方向的distance

可以看出，SharpContour这种离散分类的方案效果明显更好。