Title: 深入研究单目 3D 物体检测的输出表示

Abstract

单目 3D 对象检测旨在从单个图像中识别和定位 3D 空间中的对象。最近的研究取得了显着的进展，而所有这些研究都遵循基于 LiDAR 的 3D 检测中的典型输出表示。

然而，在本文中，我们认为现有的离散输出表示不适合单目 3D 检测。具体来说，单目3D检测只有二维信息输入，而需要输出三维检测。这一特性表明单目 3D 检测本质上不同于具有相同维度输入和输出的其他典型检测任务。尺寸差距导致估计深度误差的下限较大。

因此，我们建议将现有的离散输出表示重新表示为根据深度的空间概率分布。这种概率分布考虑了由于缺乏深度维度而导致的不确定性，使我们能够准确、全面地表示 3D 空间中的物体。

大量的实验展示了我们的输出表示的优越性。因此，我们将我们的方法应用于 12 个 SOTA 单目 3D 探测器，持续将其平均精度 (AP) 相对提高约 20%。源代码将很快公开。

==问题导读==：

所谓的离散输出指的是什么？

所谓的深度的空间概率分布指的是什么？怎么得到和利用？这么做有什么直观地好处？

一、Introduction

为了提高准确性，先前的工作做了很多尝试，包括利用估计深度图、几何性质以及网络设计

所有先前的单目作品都采用了早期检测任务中出现的典型输出表示 ，即2D框检测与对应的3D框，其中3D框被视为最终结果。然而，这种离散输出表示忽略了单目 3D 检测和其他检测任务之间固有的巨大差距。如表1所示，我们总结了不同检测任务的输入/输出及其在源域中的维度。对于单目3D检测，需要推理高维3D框，而只有低维信息输入。这个差距在其他两个检测任务中并不存在，我们的定量实验证明正是维度差距导致单目3D检测的检测精度较低。

作者分析了深度误差，得出结论：深度误差随着深度的增长呈指数增长。我们还展示了一个理论下界，它呈二次方增加（详细推导请参见第 3.2 节）。 SOTA 探测器中的深度误差和理论下限都表明，对于不靠近的物体，估计深度无法准确。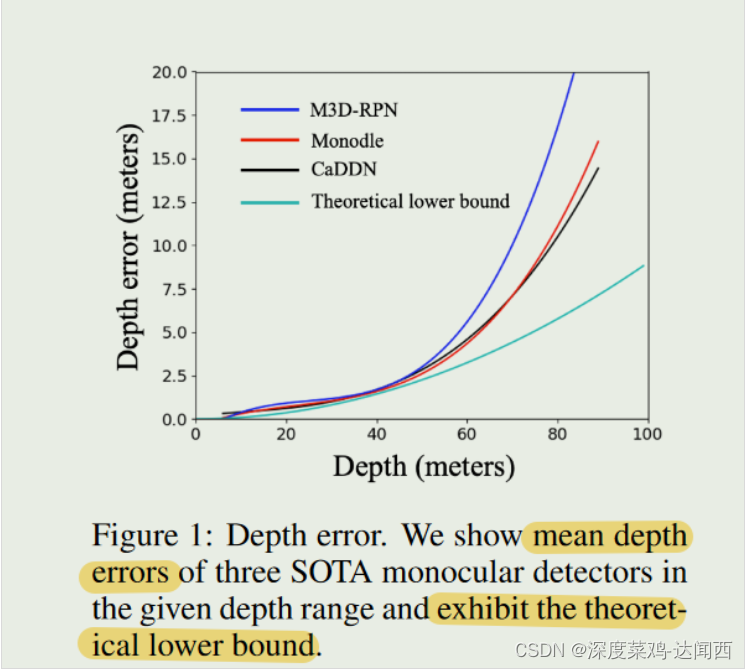从固有的尺寸差距和由此产生的大深度误差的角度来看，我们认为现有的离散深度预测表示对于单目 3D 检测来说并不是最优的。大的深度误差意味着预测的深度具有很大的不确定性，由此产生的离散3D框预测不能准确、全面地表示3D空间中的物体状态。因此，在本文中，我们的目标是重新制定单目 3D 检测的输出表示，以考虑固有的维度差距和深度不确定性。

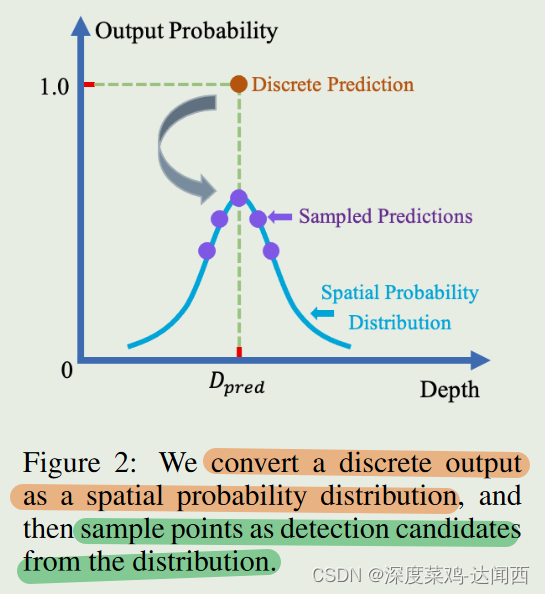
我们的重新表述包括两个步骤：

• 首先，如图 2 所示，我们使用正态分布将每个离散检测输出转换为空间概率分布，其中标准差随着深度的增长而增加。

• 其次，我们在考虑深度不确定性的同时从空间分布中采样多个3D框，并将它们视为新的检测结果。

换句话说，我们不是只输出一个离散的 3D 框，而是将 3D 框转换为 3D 空间中的连续空间概率分布，然后通过采样产生更多预测。我们的方法考虑了潜在的缺失深度维度，利用单目 3D 检测的输出表示中的深度不确定性，因此一致且显着地提高了大多数检测器的性能。

我们总结我们的主要贡献如下：

• 我们重新思考单目 3D 物体检测的基本机制，认为它与其他检测任务有着本质上的不同。根据我们的分析，我们将离散输出表示重新表述为空间概率分布，这对于单目 3D 检测来说更加合理。

• 我们已将我们的方法应用于 12 个最新的 SOTA 单目 3D 探测器，持续将其平均精度 (AP) 相对提高约 20%。值得注意的是，我们的方法可以很容易地适应任何单目 3D 探测器，这不会带来额外的成本。

问题解答：
离散指的是单独预测一个3D框是离散的，也包括了深度值是离散的。
因此作者觉得这样是不行的，需要进行正态分布式的概率分布化。

二、Related works

然而，他们没有考虑深度对位置中其他参数的影响，我们的实验表明位置中的实例深度是检测率低的主要原因。

目前的单目方法都没有考虑输出表示中维度gap带来的深度不确定性。

三、WHAT MAKES MONOCULAR 3D DETECTION CHALLENGING?

3.1 DILEMMA IN MONOCULAR 3D DETECTION

单目3D检测只有2D信息，而需要输出精确的3D信息。缺失的维度正是深度，这就是预测精确深度非常具有挑战性的原因。

即： 维度的缺失-深度，导致预测不精确。

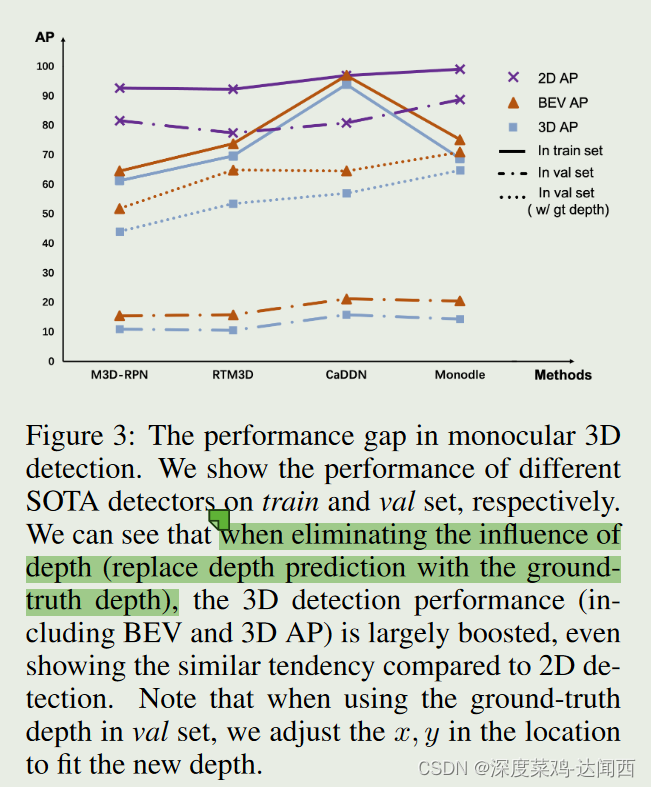
不幸的是，在物理层面上，由于尺寸差距，不可能从单个图像中推断出准确的深度，因此单目深度估计的泛化能力在很大程度上受到限制。我们进行实验来证明这一点。如图 3 所示，我们展示了不同最先进的单目检测器在训练集和验证集上的性能。我们可以观察到，训练集上的3D检测精度（包括BEV（鸟瞰图）和3D AP）很高（高于60 AP），而验证集数据的精度极低（低于20 AP）。正如预期的那样，当消除估计深度的影响（用真实深度替换深度预测）时，3D 检测性能大幅提升。验证集上改进的 3D 检测精度与训练集上的精度相当。这表明尺寸差距是单目3D检测的主要障碍。

即： 通过是否有深度条件，得出实验结果相差很大。作者认为是dimension gap导致的。

3.2 MONOCULAR DEPTH ESTIMATION ERROR LOWER BOUND

在上面有个深度误差图，其中包含了理论值下线。

即：存在固有误差，随着深度增加，误差呈现二次方形式增加

四、REFORMULATE OUTPUT REPRESENTATION FOR MONOCULAR 3D DETECTION （重新制定输出表征）

4.1 是否考虑使用先前的输出表示

考虑到单目3D检测中的维度差距，即从2D到3D的提升过程中缺少深度维度，我们重新思考检测输出表示，并提出一个问题：以前的工作采用的离散表示确实合适吗？不幸的是，我们给出了否定的答案。我们列出主要原因如下：

(i)输入不同的维度信息。仅给定 2D 信息，单目 3D 检测任务需要输出精确的 3D 信息。离散且唯一的输出无法精确反映提升预测过程中的不确定性。

(ii) 广阔的 3D 室外空间。在极其广阔的 3D 室外空间中推理出离散但精确的 3D 盒子是非常具有挑战性的。不恰当的单眼图像进一步增加了这一挑战的难度。

（iii）自动驾驶场景对安全性的高度依赖。为了避免与其他障碍物碰撞并更好地进行规划，自我汽车/机器人应该在当前场景中检测尽可能多的物体的精确位置，即追求更高的召回率，而当前的离散表示很难实现这一目标。

4.2 输出表示中的空间概率分布

基于上述分析，我们建议重新制定单目 3D 检测的输出表示。专注于处理缺失的深度维度，我们将离散检测输出转换为深度范围内的空间概率分布。考虑到已知的事实：由于精确的实例深度无法实现，因此我们可以使用空间概率分布来更全面地表示 3D 对象。这种表示还提供了更有价值的信息，例如用于下游任务的对象附近的位置不确定性，例如跟踪和规划

由于该概率分布是为了反映3D空间中深度预测的相对不确定性，因此我们使用相对概率来表示深度不确定性，因此最终的深度置信度如下：

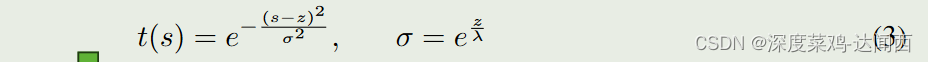
其中 s 表示任意深度，t(s) 表示相对深度置信度。随着深度的增长，正态分布的标准差也随着深度越来越难以预测而变得越来越大。结合原始置信度（通常是分类），深度 s 处物体的最终置信度为：Cs = C·t(s)。此外，由于投影关系，位置 x, y 应更改以适应新的深度 s。因此，物体在新深度 s 处的位置为 ( x z s, y z s, s)。其他参数（尺寸和方向）不变。我们将这种位置的空间概率分布称为位置分布。

当处理深度估计时，这个公式用于计算相对深度置信度（t(s)）。1. **t(s)：** 这是相对于深度 s 的深度置信度。换句话说，它表示对深度为 s 的预测的置信水平。这个值越高，就表示对深度 s 的估计越可信。2. **e^(- (s-z)^2 / σ^2)：** 这一部分使用了指数函数（e^x）来计算深度置信度。其中，x 的值为 -(s-z)^2 / σ^2。这里的 (s-z) 是
深度预测值与实际深度之间的差异，σ 是标准差（用来表示深度预测的不确定性）。这个公式的作用是，当深度预测与实际深度之间的差异较小时，
置信度会增加，反之则减小。3. **σ = e^(zλ)：** 这里定义了标准差 σ，它是一个与深度 z 相关的函数。λ 是一个常数或者一个系数，用来调节标准差的增长速度。
通常情况下，随着深度 z 的增加，标准差 σ 也会增加，因为在更远的深度上进行深度估计会更加困难，预测的不确定性也会增加。综合起来，这个公式描述了在深度估计中如何通过深度差异和标准差来计算相对深度置信度。当深度预测接近实际深度并且标准差较小时，
置信度会更高，反之则会较低。

位置分布具有多项优势。

首先，它自然适合单目 3D 探测器，因为它直接将预测深度的不确定性表达到输出中。

其次，它可以更全面、更准确地描述障碍物状态，而现有的使用离散输出表示的方法可能会对不太准确的预测过于自信。

第三，这个输出表示是灵活的，它也与之前的表示兼容（当等式3中的λ设置为−∞时）。

4.3 采样策略

通过使用每个离散原始输出的位置分布，我们得到了一系列对象的概率表示。

然后，我们从位置分布中采样位置作为新的检测结果，以评估结果。我们提出了两种采样策略并如图 4 所示。

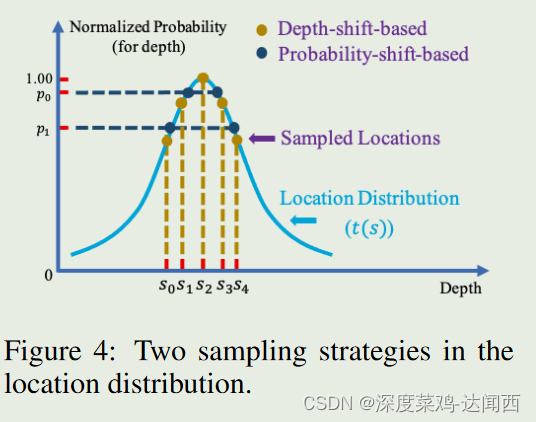
• 基于深度偏移的采样。

我们首先先定义一个深度偏移集，然后为每个原始检测输出使用该集合中的深度偏移。每个深度移动可以与位置分布中的一个位置相关联。对于原始深度为z的物体，新的检测结果为：

• 基于概率平移的采样。

与基于深度移位的采样类似，我们使用先验概率集来对位置进行采样。

五、Experiments

5.1 实施细节

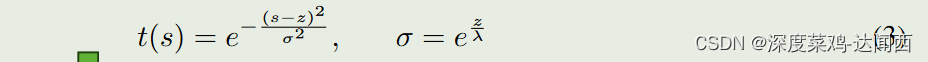
• 公式（3）中的 λ设置为 80 KITTI，160 in Waymo ；

• 我们使用集合 [±2, ±1, ±0.5, 0] 米进行基于深度间隔的采样，使用集合 [0.7, 0.8, 0.9, 1.0] 进行基于概率偏移的采样。

• 此外，考虑到近距离物体在深度估计方面足够准确，我们不会转换 10 米内物体的输出表示。

5.4 有效性分析

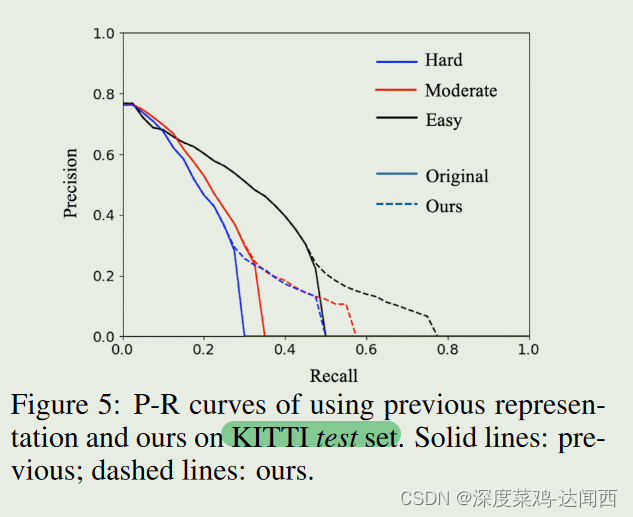
我们的输出表示在性能数字方面显示出有希望的改进。这里我们通过 P-R（精确率-召回率）曲线对改进给出更直观的解释。在图 5 中，我们显示了使用不同输出表示的单目 3D 探测器的 P-R 曲线。我们可以看到，我们的方法对高精度和低召回率区域没有影响，而对低精度和高召回率区域有效。因此，我们的方法主要是通过提高召回率来提高单目 3D 检测器的性能，从而提高配备单目 3D 检测器的系统的安全性。

5.5 Ablation Studies

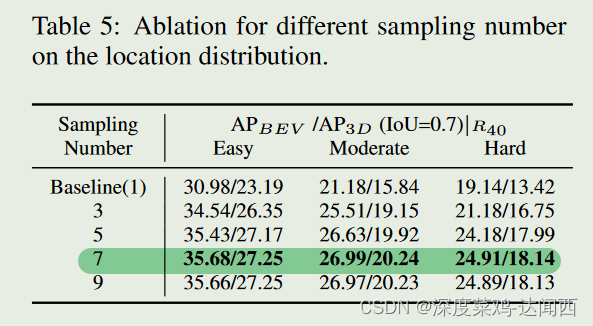
• 抽样数量的影响。从位置分布中采样位置时，采样数量也会影响精度。我们将结果显示在表5中，我们可以知道适当的采样数量是优选的。

邻近的点会比较好，不能太过于偏离。

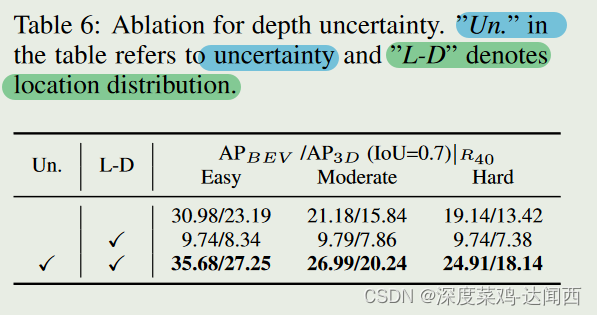
• 深度不确定性的影响。在表6中，我们显示了深度不确定性对位置分布的影响。如果采样位置的置信度不通过不确定性进行加权，则原始方法的性能会大幅下降，这证明了单目 3D 检测中深度不确定性的重要性。

深度不确定性非常重要，其他论文中也经常使用。

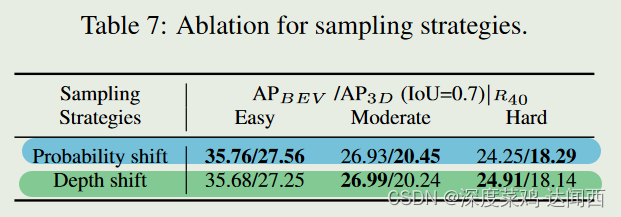
• 抽样策略的影响。我们使用提出的两种采样策略，即基于深度偏移和基于概率偏移。如表7所示，两种采样策略都为原始方法带来了显着的改进，这证明了我们方法的有效性。

现实中也是相通的，都是附近的点。不管是概率还是距离，相差不是很大；

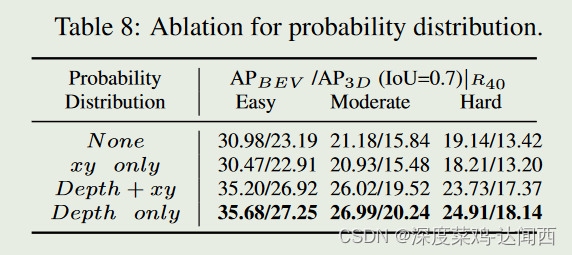
• 位置分布的影响。在本文中，我们仅变换估计深度的空间概率。为了进行全面的比较，我们还将这种变换应用于其他位置参数，即 x 和 y。我们在表8中显示了结果。我们可以看到，没有必要将概率变换为可以通过已知维度很好地推断的其他参数（x和y通常由图像上的投影表示，然后通过深度恢复）。

只用到深度上面，效果更好。

六、Conclution

在本文中，我们回顾了以前的检测任务，认为单目 3D 检测任务与其他任务有本质上的不同。对于单目 3D 检测，它缺乏深度维度，因此在看不见的数据上表现较差。我们进一步使用单目图像的深度误差下限来证明这一点。

因此，我们建议将先前的离散输出表示重新表示为空间概率分布，以考虑深度估计的不确定性。我们还提出了两种采样策略来从位置分布中采样位置。结果，实验表明我们的输出表示为大多数 SOTA 检测器带来了非常有希望的改进。此外，考虑到固有的深度不确定性，我们可以使用一些网络设计来进一步提高未来工作中的检测精度。