目录
1、数星星(《信息学奥赛一本通》 & ural 1028)
思路:
基本思路:
树状数组经典三函数:
1、lowbit()函数
2、query()函数
3、add()函数
最终代码:
2、动态求连续区间和(《信息学奥赛一本通》 & 模板)
思路:
代码:
三个主要函数:
1、lowbit()函数
2、query()函数
3、add()函数
最终代码:
3、一个简单的整数问题(《算法竞赛进阶指南》)
思路:
代码:
4、一个简单的整数问题2(POJ 2468 & 《算法竞赛进阶指南》 & kuangbin专题)
思路:
改写后的add函数:
presum函数:
最终代码:
1、数星星(《信息学奥赛一本通》 & ural 1028)
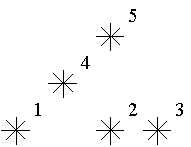
天空中有一些星星,这些星星都在不同的位置,每个星星有个坐标。
本题采用数学上的平面直角坐标系,即 x 轴向右为正方向,y 轴向上为正方向。
如果一个星星的左下方(包含正左和正下)有 k 颗星星,就说这颗星星是 k 级的。
例如,上图中星星 5 是 3 级的(1,2,4 在它左下),星星 2,4 是 1 级的。
例图中有 1 个 0 级,2 个 1 级,1 个 2 级,1 个 3 级的星星。
给定星星的位置,输出各级星星的数目。
换句话说,给定 N 个点,定义每个点的等级是在该点左下方(含正左、正下)的点的数目,试统计每个等级有多少个点。
输入格式
第一行一个整数 N,表示星星的数目;
接下来 N 行给出每颗星星的坐标,坐标用两个整数 x,y表示;
不会有星星重叠。星星按 y 坐标增序给出,y 坐标相同的按 x 坐标增序给出。
输出格式
N 行,每行一个整数,分别是 0 级,1 级,2 级,……,N−1级的星星的数目。
数据范围
1≤N≤15000
0≤x,y≤32000输入样例:
5 1 1 5 1 7 1 3 3 5 5输出样例:
1 2 1 1 0
思路:
基本思路:
由于x和y都是增序的,这意味每一次增加的星星都出现在原来星星的"右上方"
基于这个信息,我们可以发现对于每个星星每次都可以进行"查询",因为后插入的星星对其没有影响,快速地实现插入和查询两个操作:树状数组
查询后用一个level数组存储每个等级星星的数量(不算上自己)
最后把星星本身插入到树状数组中
树状数组经典三函数:
1、lowbit()函数
int lowbit(int x)
{return x&-x;
}2、query()函数
int query(int x)
{//query表示查询1~x的总和int res=0;for(int i=x;i!=0;i-=lowbit(i)){res+=tree[i];}return res;
}3、add()函数
//add表示在某一个位置加上一个数
void add(int x,int v)
{for(int i=x;i<Max;i+=lowbit(i)){tree[i]+=v;}}
最终代码:
#include<bits/stdc++.h>
//需要快速完成两个操作
//1、0~x中数的个数(优化:如果一个数出现过就是1,这样可以把求前缀的个数转化为求前缀和)
//2、添加一个数x //根据特定的需求选择特定的数据结构//本题选择树状数组(可以快速支持这两个操作)(线段树也可以)
//树状数组能操作的线段树都能操作 //树状数组的求解,下标要从1开始
using namespace std;const int N=15000+10; const int Max=32010;//坐标最大值 int n;int level[N],tree[Max];//答案、树状数组 //树状数组的三个函数int lowbit(int x)
{return x&-x;//返回的是x的二进制表示中最后一位1
} int query(int x)
{//query表示查询1~x的总和int res=0;for(int i=x;i!=0;i-=lowbit(i)){res+=tree[i];}return res;
}//add表示在某一个位置加上一个数
void add(int x,int v)
{for(int i=x;i<Max;i+=lowbit(i)){tree[i]+=v;}} int main()
{cin>>n;for(int i=0;i<n;i++){int x,y;scanf("%d%d",&x,&y);x++;//树状数组下标从1开始 int t=query(x);//统计一下1~x的数的总和 (也就是横坐标范围为1~x的星星的数量) level[t]++;//这个等级的星星数++; add(x,1);//把当前数加到树状数组当中 }for(int i=0;i<n;i++){printf("%d\n",level[i]);} return 0;
}
//树状数组能快速的求前缀和O(log n)
//能快速修改某一个数O(log n) 2、动态求连续区间和(《信息学奥赛一本通》 & 模板)
给定 n 个数组成的一个数列,规定有两种操作,一是修改某个元素,二是求子数列 [a,b] 的连续和。
输入格式
第一行包含两个整数 n 和 m,分别表示数的个数和操作次数。
第二行包含 n 个整数,表示完整数列。
接下来 m 行,每行包含三个整数 k,a,b(k=0,表示求子数列[a,b]的和;k=1,表示第 a 个数加 b)。
数列从 11 开始计数。
输出格式
输出若干行数字,表示 k=0 时,对应的子数列 [a,b]的连续和。
数据范围
1≤n≤100000
1≤m≤100000
1≤a≤b≤n
数据保证在任何时候,数列中所有元素之和均在 int 范围内。输入样例:
10 5 1 2 3 4 5 6 7 8 9 10 1 1 5 0 1 3 0 4 8 1 7 5 0 4 8输出样例:
11 30 35
思路:
边插入边查询就,用树状数组再合适不过了,也是标准的模板
代码:
三个主要函数:
1、lowbit()函数
int lowbit(int x)
{return x&-x;
}2、query()函数
int query(int x)
{//query表示查询1~x的总和int res=0;for(int i=x;i!=0;i-=lowbit(i)){res+=tree[i];}return res;
}3、add()函数
//add表示在某一个位置加上一个数
void add(int x,int v)
{for(int i=x;i<Max;i+=lowbit(i)){tree[i]+=v;}}
最终代码:
//树状数组中所有的奇数都和原数组相等 #include<bits/stdc++.h>using namespace std;const int Max=1e6+10;const int N=1e6+10;int tree[Max];//树状数组可以解决:
//某个位置上的数,加上一个数---单点修改
//求某一个前缀和---区间查询 //+差分=区间修改 单点查询 || 区间修改 区间查询 //前缀和数组不支持修改,只支持查询
//lowbit(x)=2**k(k为末尾连续0的个数) // 树状数组每个位置存的都是原数组一段数的和(从x-lowbit(x)到x)
//c[x]=value[x-lowbit(x) ,x] //树状数组的三个操作
int lowbit(int x)
{return x&-x;
}int query(int x)
{int res=0;for(int i=x;i;i-=lowbit(i)){res+=tree[i];}return res;
}int add(int x,int v)//在某一个位置x加上v (会影响到后面的树根,所以有如下写法)
{for(int i=x;i<=Max;i+=lowbit(i)){tree[i]+=v;}
}int main()
{int n,m;scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){int v;scanf("%d",&v);add(i,v);}while(m--){int op,a,b;scanf("%d%d%d",&op,&a,&b);if(op==0){int res=query(b)-query(a-1);printf("%d\n",res);}else{add(a,b);}}return 0;
} 3、一个简单的整数问题(《算法竞赛进阶指南》)
给定长度为 N 的数列 A,然后输入 M 行操作指令。
第一类指令形如
C l r d,表示把数列中第 l∼r个数都加 d。第二类指令形如
Q x,表示询问数列中第 x 个数的值。对于每个询问,输出一个整数表示答案。
输入格式
第一行包含两个整数 N 和 M。
第二行包含 N 个整数 A[i]。
接下来 M 行表示 M 条指令,每条指令的格式如题目描述所示。
输出格式
对于每个询问,输出一个整数表示答案。
每个答案占一行。
数据范围
1≤N,M≤1e5
|d|≤10000
|A[i]|≤1e9输入样例:
10 5 1 2 3 4 5 6 7 8 9 10 Q 4 Q 1 Q 2 C 1 6 3 Q 2输出样例:
4 1 2 5
思路:
树状数组+差分的应用:差分使得树状数组由单点修改+区间查询进化为了:区间修改+单点查询
经典三操作不变,只是求出来的和变成了原数组而已
代码:
//树状数组中所有的奇数都和原数组相等 #include<bits/stdc++.h>using namespace std;const int Max=1e6+10;const int N=1e6+10;int tree[Max];//树状数组可以解决:
//某个位置上的数,加上一个数---单点修改
//求某一个前缀和---区间查询 //+差分=区间修改 单点查询 || 区间修改 区间查询 //前缀和数组不支持修改,只支持查询
//lowbit(x)=2**k(k为末尾连续0的个数) // 树状数组每个位置存的都是原数组一段数的和(从x-lowbit(x)到x)
//c[x]=value[x-lowbit(x) ,x] //树状数组的三个操作
int lowbit(int x)
{return x&-x;
}int query(int x)
{int res=0;for(int i=x;i;i-=lowbit(i)){res+=tree[i];}return res;
}int add(int x,int v)//在某一个位置x加上v (会影响到后面的树根,所以有如下写法)
{for(int i=x;i<=Max;i+=lowbit(i)){tree[i]+=v;}
}int main()
{int n,m;scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){int v;scanf("%d",&v);add(i,v);}while(m--){int op,a,b;scanf("%d%d%d",&op,&a,&b);if(op==0){int res=query(b)-query(a-1);printf("%d\n",res);}else{add(a,b);}}return 0;
} 4、一个简单的整数问题2(POJ 2468 & 《算法竞赛进阶指南》 & kuangbin专题)
给定一个长度为 N 的数列 A,以及 M 条指令,每条指令可能是以下两种之一:
C l r d,表示把 A[l],A[l+1],…,A[r]都加上 d。Q l r,表示询问数列中第 l∼r个数的和。对于每个询问,输出一个整数表示答案。
输入格式
第一行两个整数 N,M。
第二行 N 个整数 A[i]。
接下来 M 行表示 M 条指令,每条指令的格式如题目描述所示。
输出格式
对于每个询问,输出一个整数表示答案。
每个答案占一行。
数据范围
1≤N,M≤1e5
|d|≤10000
|A[i]|≤1e9输入样例:
10 5 1 2 3 4 5 6 7 8 9 10 Q 4 4 Q 1 10 Q 2 4 C 3 6 3 Q 2 4输出样例:
4 55 9 15
思路:
树状数组+差分
这里需要一个小小的推导,最后得出公式:
Sn=(∑bi) * (n+1) - (∑(i*bi))) 记住即可
为了实现这个公式,维护两个数组,一个是差分树状数组tr1,另一个是存储i*tr[i]的树状差分数组
由于要为两个数组进行add操作,所以我们改写add函数(加一个参数)
改写后的add函数:
void add(LL tr[],int x,LL v)
{for(int i=x;i<=n;i+=lowbit(i)){tr[i]+=v; }
} 为了实现公式,我们写出求Sn的函数:
presum函数:
LL presum(int x)//求前缀和Sx(x及之前的和) (Sn=(∑bi) * (n+1) - (∑(i*bi)))
{LL a = query(tr1,x)*(x+1);LL b=query(tr2,x);return a-b;
}最终代码:
#include<bits/stdc++.h>using namespace std;const int N=1e5+10;typedef long long LL;int a[N];//a是原数组 LL tr1[N];//维护b【i】的前缀和 LL tr2[N];//维护i*b【i】的前缀和int n,m; int lowbit(int x)
{return x&-x;
}//这里因为要处理两个数组,所以加上数组参数
void add(LL tr[],int x,LL v)
{for(int i=x;i<=n;i+=lowbit(i)){tr[i]+=v; }
} LL query(LL tr[],int x)
{LL res=0;for(int i=x;i;i-=lowbit(i)){res+=tr[i];}return res;
}LL presum(int x)//求前缀和Sx(x及之前的和) (Sn=(∑bi) * (n+1) - (∑(i*bi)))
{LL a = query(tr1,x)*(x+1);LL b=query(tr2,x);return a-b;
}int main()
{cin>>n>>m;for(int i=1;i<=n;i++)scanf("%d",&a[i]);//形成树状差分数组 for(int i=1;i<=n;i++){int b=a[i]-a[i-1];add(tr1,i,b);add(tr2,i,(LL)b*i);} while(m--){char op[1];scanf("%s",op);if(op[0]=='C'){int l,r,v;scanf("%d%d%d",&l,&r,&v);//b[l]+=v b[r+1]-=vadd(tr1,l,v);add(tr1,r+1,-v);//b[l]+=l*v b[r+1]-=l*vadd(tr2,l,(LL)l*v);add(tr2,r+1,(LL)-(r+1)*v);}else{int l,r;scanf("%d%d",&l,&r);cout<<presum(r)-presum(l-1)<<endl;}}return 0;
}