Leetcode - 797:所有可能的路径
题目:
给你一个有 n 个节点的 有向无环图(DAG),请你找出所有从节点 0 到节点 n-1 的路径并输出(不要求按特定顺序)
graph[i] 是一个从节点 i 可以访问的所有节点的列表(即从节点 i 到节点 graph[i][j]存在一条有向边)。
示例 1:
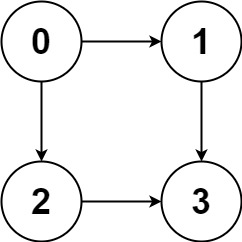
输入:graph = [[1,2],[3],[3],[]] 输出:[[0,1,3],[0,2,3]] 解释:有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3
示例 2:
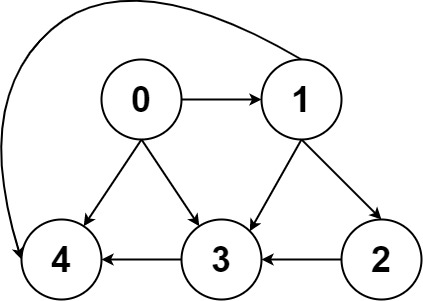
输入:graph = [[4,3,1],[3,2,4],[3],[4],[]] 输出:[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
笔记:
dfs就是递归加回溯所以和我们的递归三部曲差不多也有深搜三部曲:
1.确定参数:我们传入的参数有graph和当前节点的下标x
2.确定终止条件:如果我们遍历到了租后一个节点就返回
3.处理目前搜索节点出发的路径:
遍历graph的每个节点,将各个节点所连接的节点依次加入到path数组中,接着进行递归处理,在递归完成之后记得要回溯,将加入的节点弹出。
class Solution {
public:vector<int> path;vector<vector<int>> res;void dfs(vector<vector<int>>& graph, int x){if(x == graph.size() - 1){res.push_back(path);return;}for(int i = 0; i < graph[x].size(); i++){path.push_back(graph[x][i]);dfs(graph, graph[x][i]);path.pop_back();}}vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {path.push_back(0);dfs(graph, 0);return res;}
};Leetcode - 200:岛屿数量
题目:
笔记:
这道题跟上道题又不一样了,因为我们这道题并没有在递归处理之后进行回溯处理。那为什么这道题不用回溯而上一道题需要回溯呢?因为上一道题就像是链表的结构,一个点可以连接多个点,我们可以想象成树的结构来做,我们在遍历树寻找节点的时候在深搜的同时必须伴随着回溯使得我们不会落下任意一个路径,二这道题不一样的点在于给了我们一个二维的空间图,在寻找特定点时我们只管往前走不需要考虑有便利不到的情况因为next(x,y)会将四个方向的点都处理一遍。所以我们只需要考虑深搜三部曲即可:
确定传入的参数:传入给定的二维空间图,传入记录遍历情况的图,传入特定点的坐标。
确定终止条件:当我们遍历到的点是已经走过的或者是不符合条件的就停止搜索。
处理路径:
我们引入一个二维的数组visit来记录每个点的访问情况,当传入一个点时,我们直接将其标记为已访问过,然后我们利用opt数组来向四个方向进行搜索,如果搜索的点合法我们继续递归搜索。
在住函数中我们遍历整张图如果遍历到一点为符合搜索条件的点并且没有被访问过我们就将count+1,然后继续搜索。
class Solution {
public:int opt[4][2] = {1,0,0,-1,0,1,-1,0};void dfs(vector<vector<char>>& graph, vector<vector<bool>>& visited, int x, int y){if(graph[x][y] == '0' || visited[x][y] == true){return;}visited[x][y] = true;for(int i = 0; i < 4; i++){int nextx = x + opt[i][0];int nexty = y + opt[i][1];if(nextx >= 0 && nexty >= 0 && nextx < graph.size() && nexty < graph[0].size()){dfs(graph, visited, nextx, nexty);}else continue;}}int numIslands(vector<vector<char>>& grid) {vector<vector<bool>> visited(grid.size(), vector<bool>(grid[0].size(), false));int count = 0;for(int i = 0; i < grid.size(); i++){for(int j = 0; j < grid[0].size(); j++){if(grid[i][j] == '1' && !visited[i][j]){count++;dfs(grid, visited, i, j);}}}return count;}
};注意的点就是判断点的合法情况。
Leetcode - 547:省份数量
题目:
有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。
示例 1:
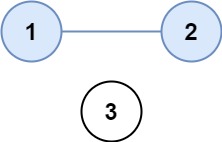
输入:isConnected = [[1,1,0],[1,1,0],[0,0,1]] 输出:2
示例 2:

输入:isConnected = [[1,0,0],[0,1,0],[0,0,1]] 输出:3
笔记:
这道题给我的第一感觉是和所有可能的路径这道题目有点像,但是这道题目不是求路径而是求省份。这也就是为什么这道题不需要用回溯的原因,并不需要我们退回到上一层递归再去找其他的路径,这道题是走过一个省份就记录了不需要回溯清楚记录。
class Solution {
public:void dfs(vector<vector<int>>& graph, vector<bool>& visited, int x){for(int i = 0; i < graph.size(); i++){if(graph[x][i] == 1 && !visited[i]){visited[i] = true;dfs(graph, visited, i);}}}int findCircleNum(vector<vector<int>>& isConnected) {int count = 0;vector<bool> visited(isConnected.size(), false);for(int i = 0; i < isConnected.size(); i++){if(!visited[i]){visited[i] = true;count++;dfs(isConnected, visited, i);}}return count;}
};这里有一个点是:为什么我们不能从x + 1开始遍历呢,因为x+1前的点一定是走过的了:
但是我们看这个报错的样例:
[[1,0,0,1],[0,1,1,0],[0,1,1,1],[1,0,1,1]]对这个样例模拟以便我们会发现我们的dfs是跳跃是的并不是依次递归城市 ,当我们跳到另一个城市时,我们就会漏掉从上一个走的城市到道歉城市这个区间,再次从当前节点dfs就会漏掉一些城市没有走但其实与其相连。
在 dfs 函数中,我们在遍历与城市 x 相连的城市时,使用的是 for 循环来遍历整个图的每个节点。在每次调用 dfs 时,我们从第一个城市开始遍历,即 i 从 0 开始。这是因为我们需要确保遍历整个图,以便找到与给定城市 x 相连的所有城市。
如果我们从 x + 1 开始遍历,这意味着我们将跳过一些城市,不会考虑它们是否与给定城市 x 相连。这可能导致一些相连的城市未被访问到,从而影响了我们对城市的数量的统计。
Leetcode - 802: 找到安全的路径:
题目:
有一个有 n 个节点的有向图,节点按 0 到 n - 1 编号。图由一个 索引从 0 开始 的 2D 整数数组 graph表示, graph[i]是与节点 i 相邻的节点的整数数组,这意味着从节点 i 到 graph[i]中的每个节点都有一条边。
如果一个节点没有连出的有向边,则该节点是 终端节点 。如果从该节点开始的所有可能路径都通向 终端节点 ,则该节点为 安全节点 。
返回一个由图中所有 安全节点 组成的数组作为答案。答案数组中的元素应当按 升序 排列。
示例 1:
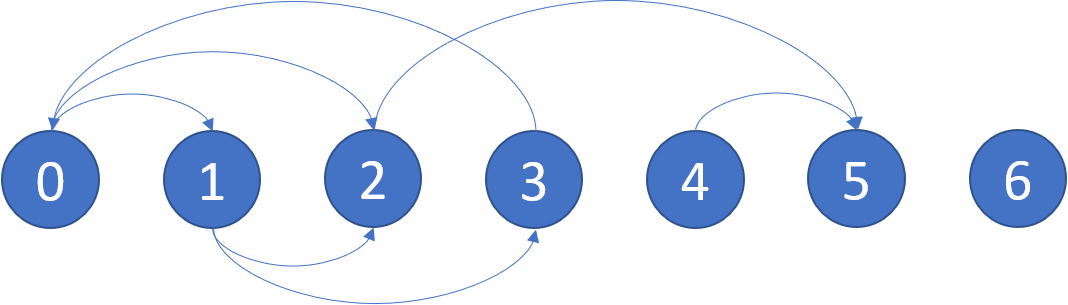
输入:graph = [[1,2],[2,3],[5],[0],[5],[],[]] 输出:[2,4,5,6] 解释:示意图如上。 节点 5 和节点 6 是终端节点,因为它们都没有出边。 从节点 2、4、5 和 6 开始的所有路径都指向节点 5 或 6 。
示例 2:
输入:graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]] 输出:[4] 解释: 只有节点 4 是终端节点,从节点 4 开始的所有路径都通向节点 4 。
笔记:
这道题我一开始的思路是将每条路径存在res数组中然后遍历res数组中的每一条路径判断其是否能到达终点,是否为安全的路径,如果是我们就将重点前的数存入最终结果数组中。
但这道题需要考虑到环路的问题:所以需要我们进一步的思考:
这道题要我们求得安全状态即为非环路上的点,所以我们就有了明确的目标,加入结果数组中的数就是出度为0的数和非环路上的数。
这样我们就可以利用dfs函数来搜索来判断当前点是否为安全状态;
这里我们的dfs函数是来判断当前点是否为安全状态,所以我们设置为bool类型,接着我们来编写:dfs函数部分:
首先我们处理当前节点,将节点的状态置为1,然后遍历该节点所连接的其余节点是否为安全状态,如果不是则返回false,遍历完所有节点我们就将该节点的状态置为2.returntrue代表我们当前节点是安全状态。
在函数的开始我们需要进行判断,如果传进来的节点正在被遍历,我们就要返回false因为已经遇到了环路,如果当前节点为安全节点则返货true
class Solution {
public:bool dfs(vector<vector<int>>& graph, vector<int>& visited, int x){if(visited[x] == 1) return false;if(visited[x] == 2) return true;visited[x] = 1;// 检查当前节点的所有连接节点中是否有不安全节点,如果有就返回。for(int i = 0; i < graph[x].size(); i++){if(!dfs(graph, visited, graph[x][i])){return false;}// 假如例题中的2相连的节点有3和5,那么在第一层循环就会直接返回false// 假如3是安全节点而5不是安全节点,那么检查完3会进行i++的操作来检查5并在检查之后返回false}// 顺利通过检查visited[x] = 2;return true;}vector<int> eventualSafeNodes(vector<vector<int>>& graph) {unordered_set<int> res;vector<int> result;vector<int> visited(graph.size());for(int i = 0; i < graph.size(); i++){if(dfs(graph, visited, i)){res.insert(i);}}result.assign(res.begin(), res.end());sort(result.begin(), result.end());return result;}
};Leetcode - 841:钥匙和房间
题目:
有 n 个房间,房间按从 0 到 n - 1 编号。最初,除 0 号房间外的其余所有房间都被锁住。你的目标是进入所有的房间。然而,你不能在没有获得钥匙的时候进入锁住的房间。
当你进入一个房间,你可能会在里面找到一套不同的钥匙,每把钥匙上都有对应的房间号,即表示钥匙可以打开的房间。你可以拿上所有钥匙去解锁其他房间。
给你一个数组 rooms 其中 rooms[i] 是你进入 i 号房间可以获得的钥匙集合。如果能进入 所有 房间返回 true,否则返回 false。
示例 1:
输入:rooms = [[1],[2],[3],[]] 输出:true 解释: 我们从 0 号房间开始,拿到钥匙 1。 之后我们去 1 号房间,拿到钥匙 2。 然后我们去 2 号房间,拿到钥匙 3。 最后我们去了 3 号房间。 由于我们能够进入每个房间,我们返回 true。
示例 2:
输入:rooms = [[1,3],[3,0,1],[2],[0]] 输出:false 解释:我们不能进入 2 号房间。
笔记:
这道题我一开始的思路是遍历所有房间,如果找到了一间房间可以两桶所有房间就返回true,这样明显是不对的,因为我们只能从房间0出发。
所以我们的dfs函数只用来处理visited数组,传入节点后将其状态置为1,然后遍历传入节点所连的节点,判断是否被访问过,若果没有就进入递归。在住函数中我们现将0节点传入dfs函数然后遍历visited数组看有没有全部访问完毕即可。
class Solution {
public:void dfs(vector<vector<int>>& graph, vector<bool>& visited, int node){visited[node] = true;for(int i = 0; i < graph[node].size(); i++){if(!visited[graph[node][i]]){dfs(graph, visited, graph[node][i]);}}}bool canVisitAllRooms(vector<vector<int>>& rooms) {vector<bool> visited(rooms.size(), false);dfs(rooms, visited, 0);for(int i = 0; i < rooms.size(); i++){if(!visited[i]){return false;}}return true;}
};Leetcode - 1376:通知所有员工所需的时间:
题目:
公司里有 n 名员工,每个员工的 ID 都是独一无二的,编号从 0 到 n - 1。公司的总负责人通过 headID 进行标识。
在 manager 数组中,每个员工都有一个直属负责人,其中 manager[i] 是第 i 名员工的直属负责人。对于总负责人,manager[headID] = -1。题目保证从属关系可以用树结构显示。
公司总负责人想要向公司所有员工通告一条紧急消息。他将会首先通知他的直属下属们,然后由这些下属通知他们的下属,直到所有的员工都得知这条紧急消息。
第 i 名员工需要 informTime[i] 分钟来通知它的所有直属下属(也就是说在 informTime[i] 分钟后,他的所有直属下属都可以开始传播这一消息)。
返回通知所有员工这一紧急消息所需要的 分钟数 。
示例 1:
输入:n = 1, headID = 0, manager = [-1], informTime = [0] 输出:0 解释:公司总负责人是该公司的唯一一名员工。
示例 2:

输入:n = 6, headID = 2, manager = [2,2,-1,2,2,2], informTime = [0,0,1,0,0,0] 输出:1 解释:id = 2 的员工是公司的总负责人,也是其他所有员工的直属负责人,他需要 1 分钟来通知所有员工。 上图显示了公司员工的树结构。
笔记:
这道题就有前几道题的影子,就是处理方式不一样罢了,这里我们需要先把初始节点的数组也就是头结点找出来:
for(int i = 0; i < n; i++){if(manager[i] != -1){mng[manager[i]].push_back(i);}}接着我们就要进行递归dfs深搜了,将每个节点的路径搜素一遍,因为需要通知到所有员工所以跟之前钥匙与房间也差不多。接下来我们求dfs的函数:首先我们考虑传入的参数:因为要考虑时间所以再传入时间队列:
dfs函数思路:
首先将传入的node状态置为已访问,接着搜索node的下属即其所连的节点,判断这些节点各自是否访问过如果没有访问过我们就进行递归调用dfs函数求得tim额,最后返回time。
class Solution {
public:int dfs(vector<vector<int>>& mng, vector<int>& informTime, vector<bool>& visited, int node){visited[node] = true;int time = 0;for(int i = 0; i < mng[node].size(); i++){if(!visited[mng[node][i]]){time = max(time, dfs(mng, informTime, visited, mng[node][i]));}}return time + informTime[node];}int numOfMinutes(int n, int headID, vector<int>& manager, vector<int>& informTime) {vector<vector<int>> mng(n);for(int i = 0; i < n; i++){if(manager[i] != -1){mng[manager[i]].push_back(i);}}vector<bool> visited(n, false);return dfs(mng, informTime, visited, headID);}
};这道题中需要注意的点是headid是总负责人,在建立关系表的过程中我们要特殊判断当前节点不能是主负责人,因为主负责人的manager是-1.
Leetcode - 1466:重新规划路线
题目:
n 座城市,从 0 到 n-1 编号,其间共有 n-1 条路线。因此,要想在两座不同城市之间旅行只有唯一一条路线可供选择(路线网形成一颗树)。去年,交通运输部决定重新规划路线,以改变交通拥堵的状况。
路线用 connections 表示,其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。
今年,城市 0 将会举办一场大型比赛,很多游客都想前往城市 0 。
请你帮助重新规划路线方向,使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。
题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。
示例 1:
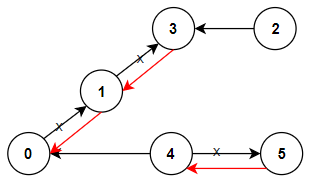
输入:n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]] 输出:3 解释:更改以红色显示的路线的方向,使每个城市都可以到达城市 0 。
示例 2:

输入:n = 5, connections = [[1,0],[1,2],[3,2],[3,4]] 输出:2 解释:更改以红色显示的路线的方向,使每个城市都可以到达城市 0 。
示例 3:
输入:n = 3, connections = [[1,0],[2,0]] 输出:0
笔记:
这个是真么什么思路,主要是对于求最短修改数这块我不知该如何下手,这道题我觉得跟之前要是与房间的模型大致一样,但是这个修改路线实在是难以下手,
这道题也是用了大量的陌生结构来解:
(1)创建pair数组类型:
// 我们在这里需要对边进行标记,这里我们需要出发的节点到下一节点:
// [start] --> (end, index)
// 这里用到的就不再是标准的队列结构了,因为这是一个一对二的关系,而队列只是一一对应的关系,所以就要用到pair重组类型来表示:
vector<vector<pair<int, bool>>> a
// 对该结构进行插入操作:
a[i].push_back(make_pair(int, bool))// 对组成pair类型中的特定一个元素进行操作:
a[i] -> first || a[i] -> second只要我们能对边进行特定的标记之后就很好处理了,对每一条边,如果边指向近‘0’节点,那么就将这条边的end -> second置为false,如果反过来就置为 -> true。接着就是从0节点开始深度搜索,如果搜索的节点是true就count++并将该边置为false。处理整张图。
class Solution {
public:void dfs(vector<vector<pair<int, bool>>>& graph, vector<bool>& visited, int node, int& count){visited[node] = true;for(vector<pair<int, bool>>::iterator it = graph[node].begin(); it != graph[node].end(); it++){if(!visited[it -> first]){if(it -> second){it -> second = false;count++;}dfs(graph, visited, it -> first, count);}}}int minReorder(int n, vector<vector<int>>& connections) {vector<bool> visited(n, false);// 获取graph数组vector<vector<pair<int, bool>>> graph(n);for(int i = 0; i < connections.size(); i++){graph[connections[i][0]].push_back(make_pair(connections[i][1], true));graph[connections[i][1]].push_back(make_pair(connections[i][0], false));}int count = 0;dfs(graph, visited, 0, count);return count;}
};