第13届蓝桥杯省赛 ---- C/C++ C组

文章目录

1. 字母排列
2. 特殊时间
3. 纸张尺寸
4. 求和
5. 数位排序
6. 选数异或
7. 消除游戏
8. 重新排序
9. 技能升级
10. 重复的数

第13届蓝桥杯省赛C/C++组题解。

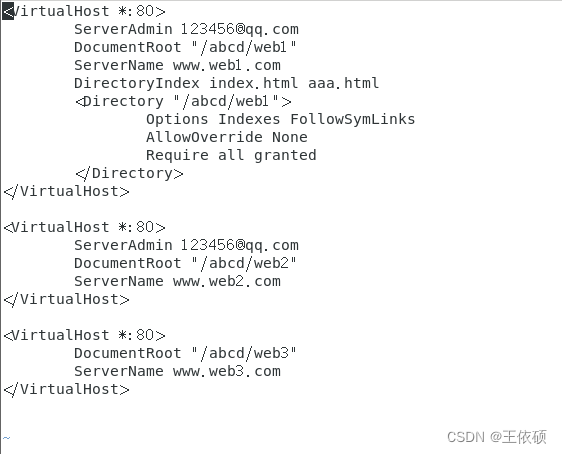
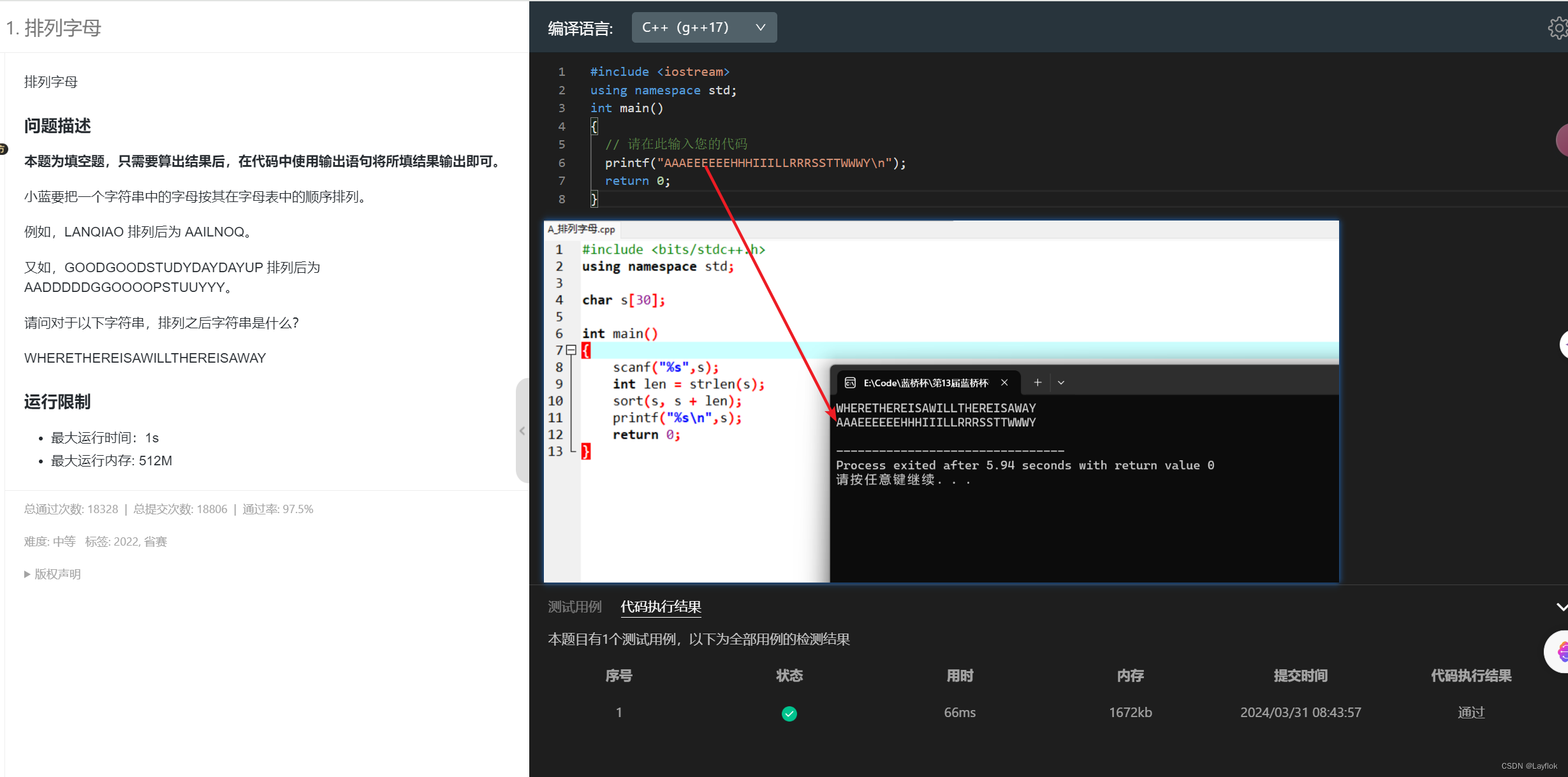
1. 字母排列

在这里插入图片描述
这道题直接排序输出就好了。

#include <bits/stdc++.h>
using namespace std;char s[30];int main()
{scanf("%s",s);int len = strlen(s);sort(s, s + len);printf("%s\n",s);return 0;
}

2. 特殊时间

在这里插入图片描述
这道题目的核心就是说年份是不需要管的，所以只需要求出月日和时分即可。
4 × 月日（合法）× 时分（合法）即可。
这篇题解非常的nice。

#include <iostream>
using namespace std;
int main()
{// 请在此输入您的代码//年：****  A行//月**日**  B行//时**分**  C行//年份无论闰年平年没有影响。从月份入手，分两种情况://   零开头：01 02两种 所以第二行是0111或0222 共有2*4*4=32种//   一开头：10 11 12//           10： 1000（×）  1011（√） 4*1*4=16种//           11: 11*1—— 1101（√） 1111（×）1121（√）1131（×）1141..无  2种 2*4*4=32种//               111*—— 1110（√） 1111（×）1112（√） 4*2*4=32种//                      1113（3种）1114（3种）1115（3种）4*3*3=36种//                      1116、1117、1118、 1119 （2种）  4*4*2=32种//           12： 1211 （√）  1222（√） 4*2*4=32种//   总数为:4*4*(2+1+2+2+2+2)+4*3*3=212;cout<<4*4*(2+1+2+2+2+2)+4*3*3<<endl;return 0;
}
出处：蓝桥杯官网，特殊事件题目：
博主: 张小五。

3. 纸张尺寸

在这里插入图片描述
题目要求：
最开始给定这纸的最开始大小记作A0，然后每次选最长的那个边进行对折，具体对折多少次看所输入的是A（0 ~ 9），对折(0 ~ 9)次。
思路：
每次记录当前最大的边是哪一个，然后对其进行折半之后，他就变成最小的了，依次循环即可。

#include <bits/stdc++.h>
using namespace std;struct Page
{int ma = 1189,mi = 841;
}p;
char op[5];int main()
{scanf("%s",op);int n = op[1] - '0';for (int i = 0; i < n; i++){int t = p.ma / 2;p.ma = p.mi;p.mi = t;}printf("%d\n%d",p.ma,p.mi);return 0;
}

4. 求和

在这里插入图片描述
题目要求：
给定一个数组，将其每个按照所给的公式进行求和。
思路：
暴力：
这道题暴力的做法就是进行双for循环就可以拿到60的分数。

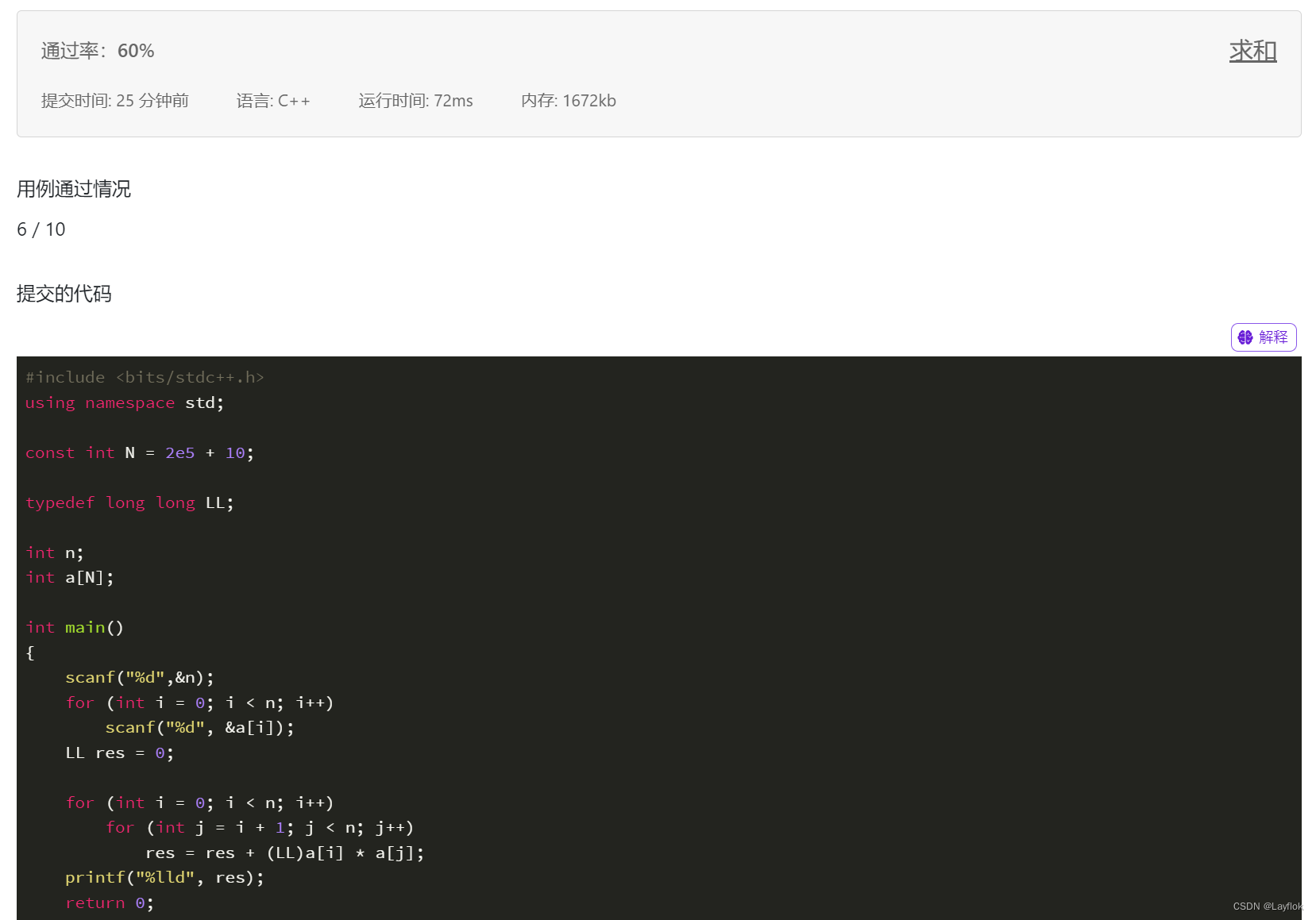
前缀和：
但是我们可以将题目中所给的公式进行简单的合并:
a1 * a2 + a1 * a3 + ...... a1 * an = a1 * (a2 + a3 + a4 + .... an);
a2 * a3 + a2 * a4 + ...... a2 * an = a2 * ( a3 + a4 + .... an);

#include <bits/stdc++.h>
using namespace std;const int N = 2e5 + 10;typedef long long LL;int n;
int a[N], s[N];
int main()
{scanf("%d",&n);for (int i = 1; i <= n; i++){scanf("%d",&a[i]);s[i] = s[i - 1] + a[i];}LL res = 0;for (int i = 1; i <= n; i++){res = res + (LL)a[i] * (s[n] - s[i]);}printf("%lld", res);return 0;
}
// a1 * a2 + a1 * a3 + ...... a1 * an = a1 * (a2 + a3 + a4 + .... an);
// a2 * a3 + a2 * a4 + ...... a2 * an = a2 * (     a3 + a4 + .... an);
//                                      a3 * (          a4 + .... an);

5. 数位排序

在这里插入图片描述
题目要求：
输入两行n和m表示从1~n这些数字中，对其按照数位之和优先，其次数的大小，的方式从小到达排序，然后排序后第m个数是多少。
思路：
将其录入到一个数组中去，然后对数组进行排序就好了。直接使用sort函数就可以过.

#include <bits/stdc++.h>
using namespace std;const int N = 1e6 + 10;
int n,m;
int a[N];int dig_sum(int x)
{int sum = 0;while (x){sum += x % 10;x /= 10;}return sum;
}bool cmp(int a, int b)
{int x = dig_sum(a), y = dig_sum(b);if (x != y)return x < y;else return a < b;
}int main()
{scanf("%d%d",&n,&m);for (int i = 1; i <= n; i++)a[i] = i;sort(a + 1, a + 1 + n, cmp);printf("%d\n",a[m]);return 0;
}

6. 选数异或

在这里插入图片描述
题目要求：
第一行输入三个数n,m,k 分别表示数组的长度，以及询问次数，和目标是x.
在m次询问中，每次在[l,r]的区间内，是否有两个数a ^ b = x.
思路：

题目要求是a ^ b = x根据异或的规则同样可以等价于a = b ^ x.
所以我们假设b在左边，而a在右边，那么问题就能转化为在b的左边是否有一个数使b ^ x = a，我们暂且记作f[b]存放着b ^ x = a中a的下标。
因为遍历数组的从左往右的遍历的，所以遍历到b的时候一定遍历过a 这样子我们在遍历的时候用哈希表来记录a出现时候的下标。
这样子问题就变成了在[l,r]内的每一个数是否有l<= f[b] <= r,而对此还可以进行优化。
我们使用一个g[b]来代表b前面的离b最近的a。
g[b] = max(g[b - 1], f[b ^ x])
那么我们在m次讯问中就可以直接用g[r]是否大于等于l.
距离r位置最近的b ^ x = a a的下标大于等于l.
如果还不懂可以看看这篇视频题解

#include <bits/stdc++.h>
using namespace std;const int N = 1e5 + 10, M = (1 << 20) + 10;int n, m, x;
int f[M], g[N];int main()
{scanf("%d%d%d",&n, &m, &x);for (int i = 1; i <= n; i++){int b;scanf("%d",&b);g[i] = max(g[i - 1], f[b ^ x]);f[b] = i;}while (m --){int l, r;scanf("%d%d",&l, &r);if (g[r] >= l)printf("yes\n");elseprintf("no\n");}return 0;
}

7. 消除游戏

在这里插入图片描述
题目要求:
给一个字符串，按照其所给的提示规则，删除边缘字符串，注意一次操作可以删除整个字符串的边缘字符，而不是像栈那样子一个一个删除。
比如： edda 可以删除ed，但是字符串不会变成da，而是你发现ed和da都可以删除，然后同时删除。此字符串就变成空的了。
思路：
暴力模拟：

只需要挨个遍历s中的元素就好了，只要满足题目中的两个条件，那么其就是边缘字符，将其标记为被删节点。
然后将所有的被删节点删除，重新构造字符串s
最直观的办法肯定还是暴力，但肯定会超时的，可以过66%。

#include <bits/stdc++.h>using namespace std;const int N = 1e6 + 10;
char s[N];
bool st[N];//重新构造删除后的字符串
void Helper(int& len)
{char t[N];int size = 0;for (int i = 0; i < len; i++){if (!st[i])t[size++] = s[i];}t[size++] = '\0';strcpy(s, t);len = strlen(s);memset(st, 0, sizeof st);
}int main()
{scanf("%s", s);int len = strlen(s);while (len){bool flag = true;   //记录该操作中是否进行删除操作for (int i = 1; i < len - 1 && len != 0; i++){if (s[i] == s[i - 1] && s[i] != s[i + 1])st[i] = true, st[i + 1] = true, flag = false;else if (s[i] != s[i - 1] && s[i] == s[i + 1])st[i - 1] = true, st[i] = true, flag = false;}Helper(len);if (flag)   //如果没有操作，直接返回break;}if (len == 0)printf("EMPTY\n");elseprintf("%s", s);return 0;
}

方法二：利用双链表 + 备删除节点
我们从暴力模拟的算法中发现，这个算法有两点可以进行优化。
第一点就是说，对于字符串的重塑，也就是删除待删元素，需要重新对字符串进行一次遍历，删除操作过去繁琐。
第二点是，我们删除了节点后，其实受影响的只有删除的节点的左右两边是遭受影响的，所以只需要构造一个备删数组q里面存放的就是备删节点，下次直接遍历q就好了。
我们通过这两步的优化就会成功的解决该题。

#include <bits/stdc++.h> 
using namespace std;const int N = 1e6 + 10;
char s[N];			//字符串 
int l[N], r[N];		//双链表 
bool st[N];			//该节点是否删除。 
vector<int> q,w;	//q是备删节点， w是待删节点//插入待删节点 
void insert(int k)
{if (!st[k]){st[k] = true;w.push_back(k);}
}void filter_del()
{w.clear();for (int t : q){int a = l[t], b = t, c = r[t];//从备选节点中去看 是否可删。 if (s[a] == s[b] && s[b] != s[c] && s[c] != '#')insert(b), insert(c);if (s[a] != s[b] && s[b] == s[c] && s[a] != '#')insert(a), insert(b);}
}int main()
{scanf("%s", s + 1);int n = strlen(s + 1);//创建双链表，以及备删节点 for (int i = 1; i <= n; i++){l[i] = i - 1, r[i] = i + 1;q.push_back(i);}//设置哨兵位。 r[0] = 1, l[n + 1] = n;s[0] = '#', s[n + 1] = '#';while (1){filter_del();//如果待删节点为空，就说明已经没有可以删除的了，结束循环即可if (w.empty())	break;//重新构造备删节点 q.clear(); for (int t : w){//左 中 右 --- a b c    i - 1   i    i + 1int a = l[t], b = t, c = r[t];if (a != 0 && !st[a] && (q.empty() || q.back() != a))q.push_back(a);if (c != n + 1 && !st[c])q.push_back(c);r[a] = c;l[c] = a;} }if (r[0] == n + 1)printf("EMPTY\n");elsefor (int i = r[0]; i != n + 1; i = r[i])printf("%c", s[i]);return 0;
}

8. 重新排序

在这里插入图片描述
题目要求：
给定一个数组，然后输入m次询问，每次求出[l,r]当前区间的和，然后将所有次的和加在一起，但是还没有完，需要我们对所给的数组进行一次排序，将所选的[l,r]内的数重新更换，使其两次和相比之下，最多能增加多少。
思路：

我们可以利用差分数组来求前缀和，首先将原数组录入到w中去，然后创建一个s数组，里面存放的是刚开始的差分值，最后需要对其进行求解前缀和。
这里说明一下如何利用差分前缀和数组求解[l,r]内的和。
正常来说，如果我们得到了一个前缀和数组，我只需要将其按照公式s[r] - s[l - 1]就能够得到[l,r]的前缀和了。
还有一种方式也是可以的，如下图所示，左边是举一个例子，右边是对应的题目的。
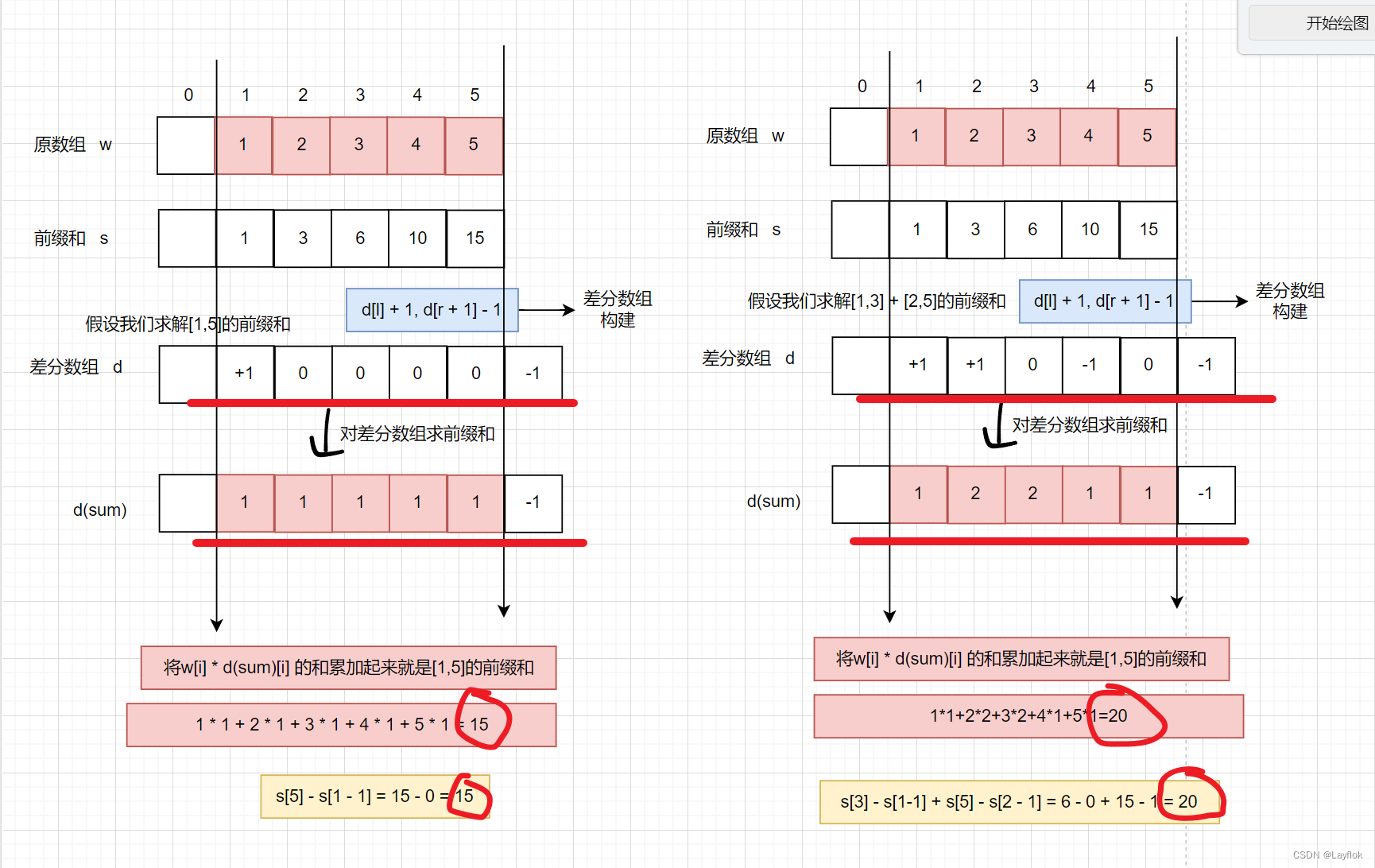
我们会利用这种方式求解前缀和后，这道题就简单了。
通过排序不等式可以退出，只要两个序列全部以递增的形式，一一对应相乘，最后的结果一定是最大的。
所以将两个数组排序之后，对其一一对应的相乘，即可求出最大值。
两个和相减即可。

#include <bits/stdc++.h>
using namespace std;const int N = 1e5 + 10;typedef long long LL;int n, m;
int w[N], s[N];int main()
{scanf("%d", &n);for (int i = 1; i <= n; i++)scanf("%d", &w[i]);scanf("%d", &m);for (int i = 0; i < m; i++){int l, r;scanf("%d%d", &l, &r);s[l]++, s[r + 1]--;}for (int i = 1; i <= n; i++)s[i] += s[i - 1];LL sum1 = 0;for (int i = 1; i <= n; i++)sum1 += (LL)s[i] * w[i];sort(w + 1, w + 1 + n);sort(s + 1, s + 1 + n);LL sum2 = 0;for (int i = 1; i <= n; i++)sum2 += (LL)s[i] * w[i];printf("%lld\n", sum2 - sum1);return 0;
}

9. 技能升级

在这里插入图片描述
题目要求：
第一行输入n和m分别代表有n个技能和可以进行m次加点，需要我们在m此操作内是攻击力加到最大，第一次增加Ai个攻击力，下次就只能增加Ai - Bi个攻击力了,依次类推。
思路：
暴力
这题暴力自然也是能做的，每次选出增加技能点最多的，然后下次使Ai = Ai - Bi.直到m次结束。

那么我们就可以维护一个大根堆，每次直接去除堆顶的元素，然后再插入新的。
依次类推即可

这种做法只能得50%的分数。

#include <bits/stdc++.h>
using namespace std;typedef pair<int,int> PII;
typedef long long LL;int n, m;priority_queue<PII, vector<PII>, less<PII> >heap;int main()
{scanf("%d%d", &n, &m);for (int i = 0; i < n; i++){int a, b;scanf("%d%d", &a, &b);heap.push({a, b});}LL res = 0;while (m--){auto t = heap.top();heap.pop();res += t.first;heap.push({t.first - t.second, t.second});}printf("%lld\n", res);return 0;
}

二分 + 多路归并
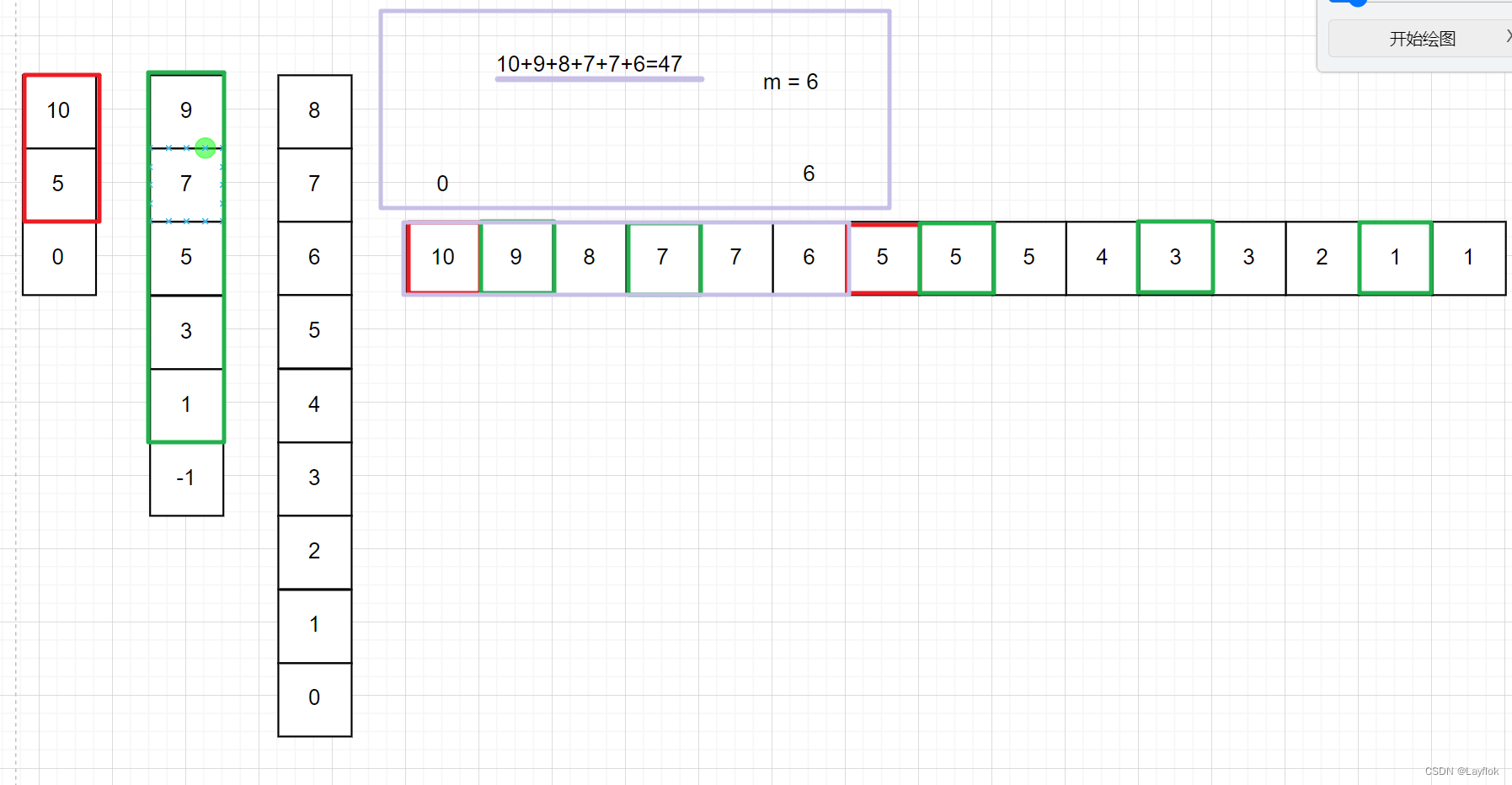
还有一种解法，我们可以将所给的技能点数想象成一堆等差数列。
然后将等差数列的每一项全部展开，将其从大到小排序，前m项就是答案。
如下图所示：
在这里插入图片描述
因为它的数据范围非常的大，如果真的将全部的等差数列一一展开，事件和空间的开销同样也是巨大的，还不如优先队列来的好，所以我们要在这一种思想上进行优化。

我们首先得到的结论就是说前m个项加起来一定是最后的值，这个是毋庸置疑的。
我们设x为所有展开数列的第m项，我们就可以推到一个不等式出来:
大于等于x的数的个一定大于等于m
接下来我们来二分枚举一下数x。
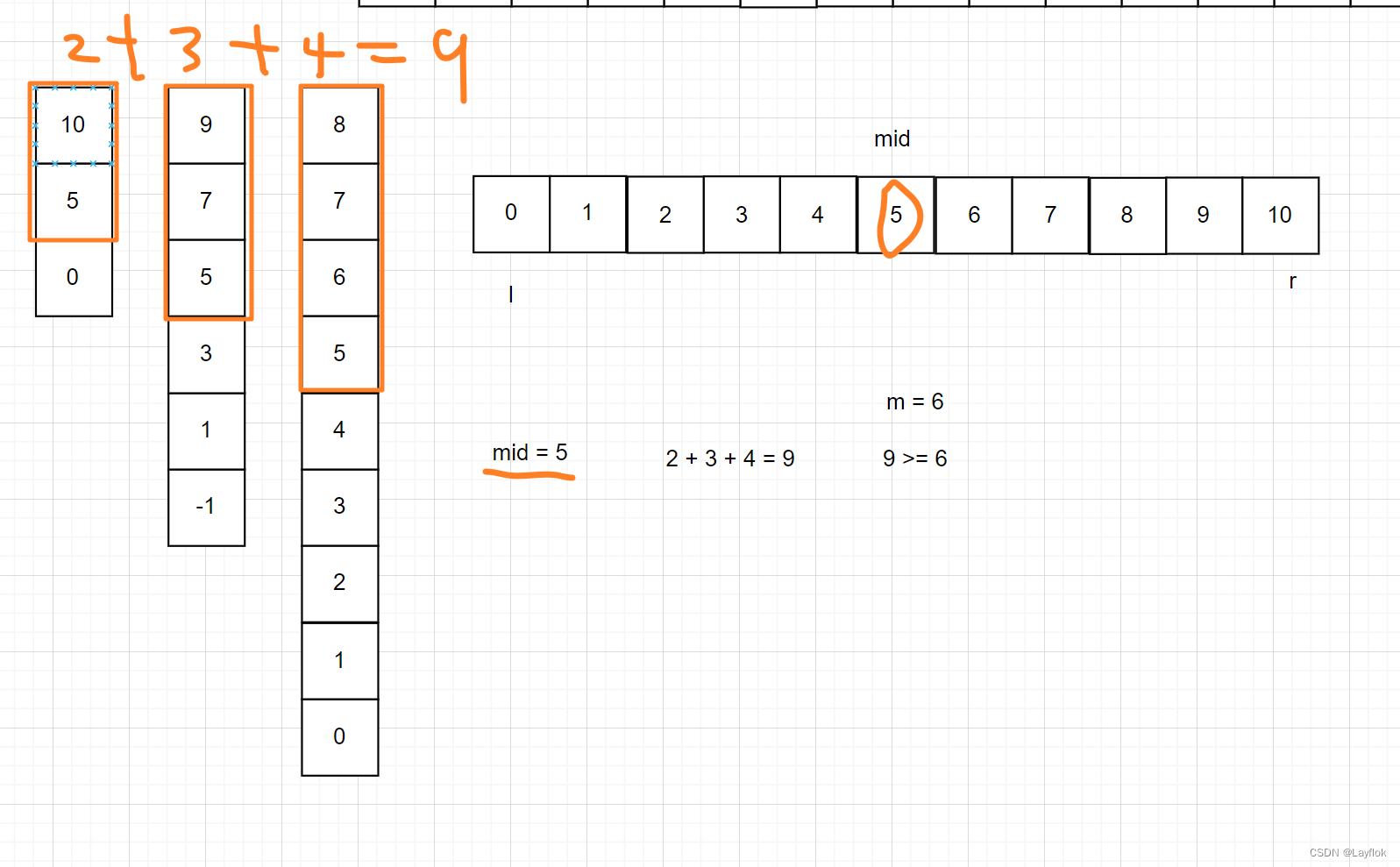
由此就可以发现，当数枚举到5的时候，其所有大于等于5的项有9个，那么在5之前的数，他比5都小，所以mid左边的数全部不用再看了。
使l = mid 即可。
那么对应的二分模板就有了。
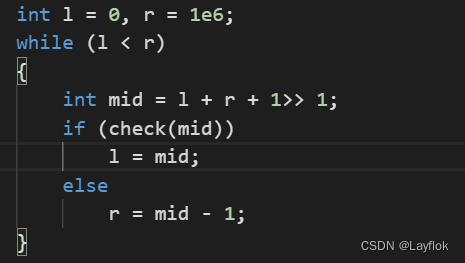
至于如何算一个等差数列中有多少项大于等于x，对于整个问题是有公式可以解决的，所以计算其的事件复杂度是O(1)的。
>= x 有多少个： (首项 - x) / 公差 + 1
到了这里，x已经求出来了，最后将所有序列中 >= x的所有项的和加起来就是答案了。
需要用到几个公式:
设求a1 到 x的和。
项数 = （首项 - x）/ 公差 + 1
末项 = 首项 + （项数 - 1） * 公差
注意该题中公差是负的，所以应该变成负号.
s[x] = (首项 + 尾项) * 项数/ 2

最后注意可能加了多个重复的数，比如下面这种情况：
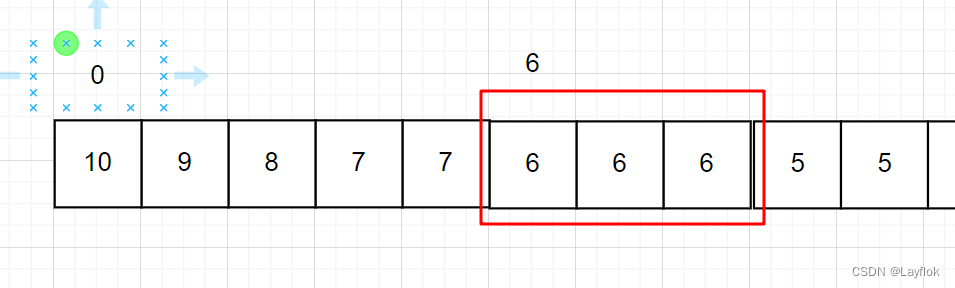
在这里插入图片描述
因为我们在遍历每一个序列的时候是将所有大于等于6的数全部加入，一个6多次相加，我们只需要将多余的6全部减去就好了。

#include <bits/stdc++.h>
using namespace std;const int N = 1e5 + 10;typedef long long LL;int n, m;
int a[N], b[N]; //a[i] 代表第i个序列的首项， b[i]代表第i个序列的公差。bool check(int mid)
{LL res = 0;for (int i = 0; i < n; i++)if (a[i] >= mid)res += (LL)(a[i] - mid) / b[i] + 1;return res >= m;
}int main()
{scanf("%d%d", &n, &m);for (int i = 0; i < n; i++)scanf("%d%d", &a[i], &b[i]);//开始二分，找一个数 x 为边界， 使得 x >= m， 将前面所有的项 + 到 x即是答案。int l = 0, r = 1e6;while (l < r){int mid = l + r + 1>> 1;if (check(mid))l = mid;elser = mid - 1;}LL res = 0, cnt = 0;for (int i = 0; i < n; i++)if (a[i] >= r){int c = (a[i] - r) / b[i] + 1;  //项数长度cnt += c;                       int end = a[i] - (c - 1) * b[i];    //末项 = 首项 + 项数 - 1 * 公差res += (LL)(a[i] + end) * c / 2;}printf("%lld\n", res - (cnt - m) * r);return 0;
}

10. 重复的数

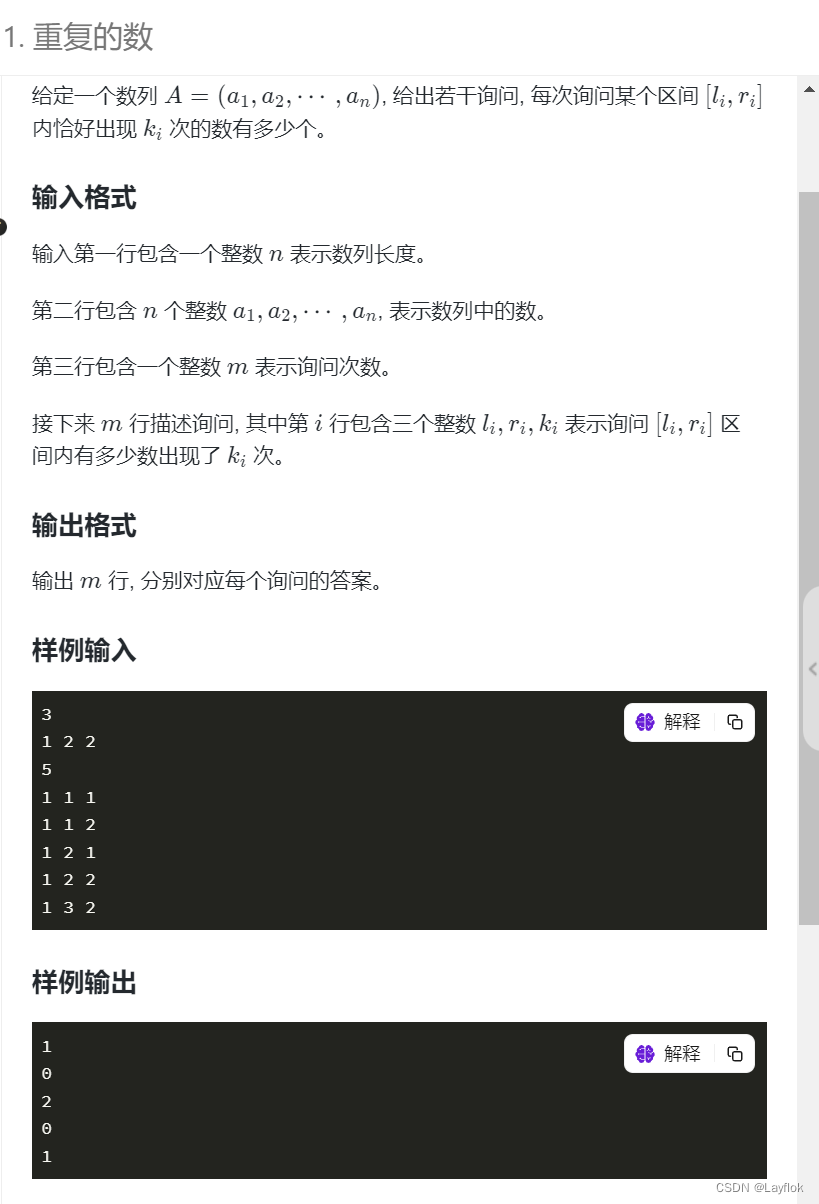
在这里插入图片描述
题目要求：
这道题目要求我们在一个数组中找，找到区间[l,r]内出现了k次的数的个数。
一定要读清楚题目，我最开始还以为是k出现的次数。
思路：
暴力
这道题暴力算法也能获得50%的分数，用一个哈希表记录当前区间内各个数出现的次数，然后找出出现了k的数就好了。

#include <bits/stdc++.h>
using namespace std;const int N = 1e5 + 10;int n, m;
int a[N], h[N];int main()
{scanf("%d", &n);for (int i = 1; i <= n; i++)scanf("%d", &a[i]);scanf("%d", &m);while (m --){int l, r, k;scanf("%d%d%d",&l, &r, &k);int cnt = 0, ma = 0;memset(h, 0, sizeof h);for (int i = l; i <= r; i++){ma = max(ma, a[i]);h[a[i]]++;}for (int i = 0; i <= ma; i++)if (h[i] == k)cnt++;printf("%d\n",cnt);}return 0;
}

莫队
简单来讲解一下莫队算法：
莫队算法可以解决离线问题，对于所有询问区间，在 O(n $\sqrt{n}$ )的时间复杂度内求出所有的答案。
所以对于这道题来讲，肯定是不会超时的。
关于莫队的更细的知识点，可以去这里看看.
其实会莫队这个算法后，发现这道题目，就是一个简单的模板题了，只需要修改两个函数就好了。
莫队的模板：

对数组进行分块，分成 $\sqrt{n}$ 块区域。
录入所有的询问m，将m个区间[l,r]将l所在的块进行第一个排序的关键字，然后r做为第2个关键字（从小到大）。
开始遍历所有的询问区间，进行相对应的4种修改。

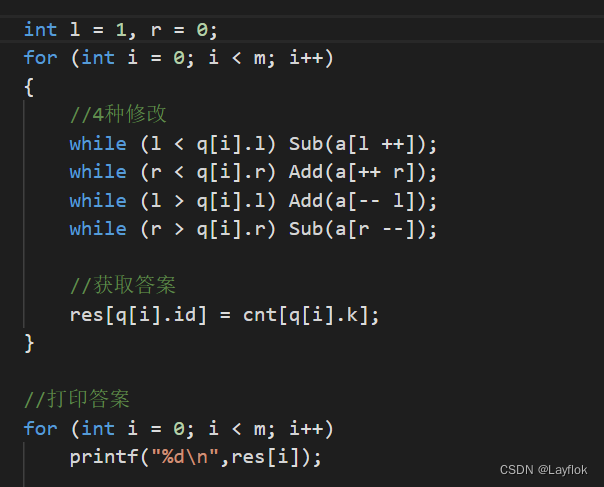
以上就是莫队的模板，获取答案那一步不是固定的，是这道题目的。
下面是整体的模板：

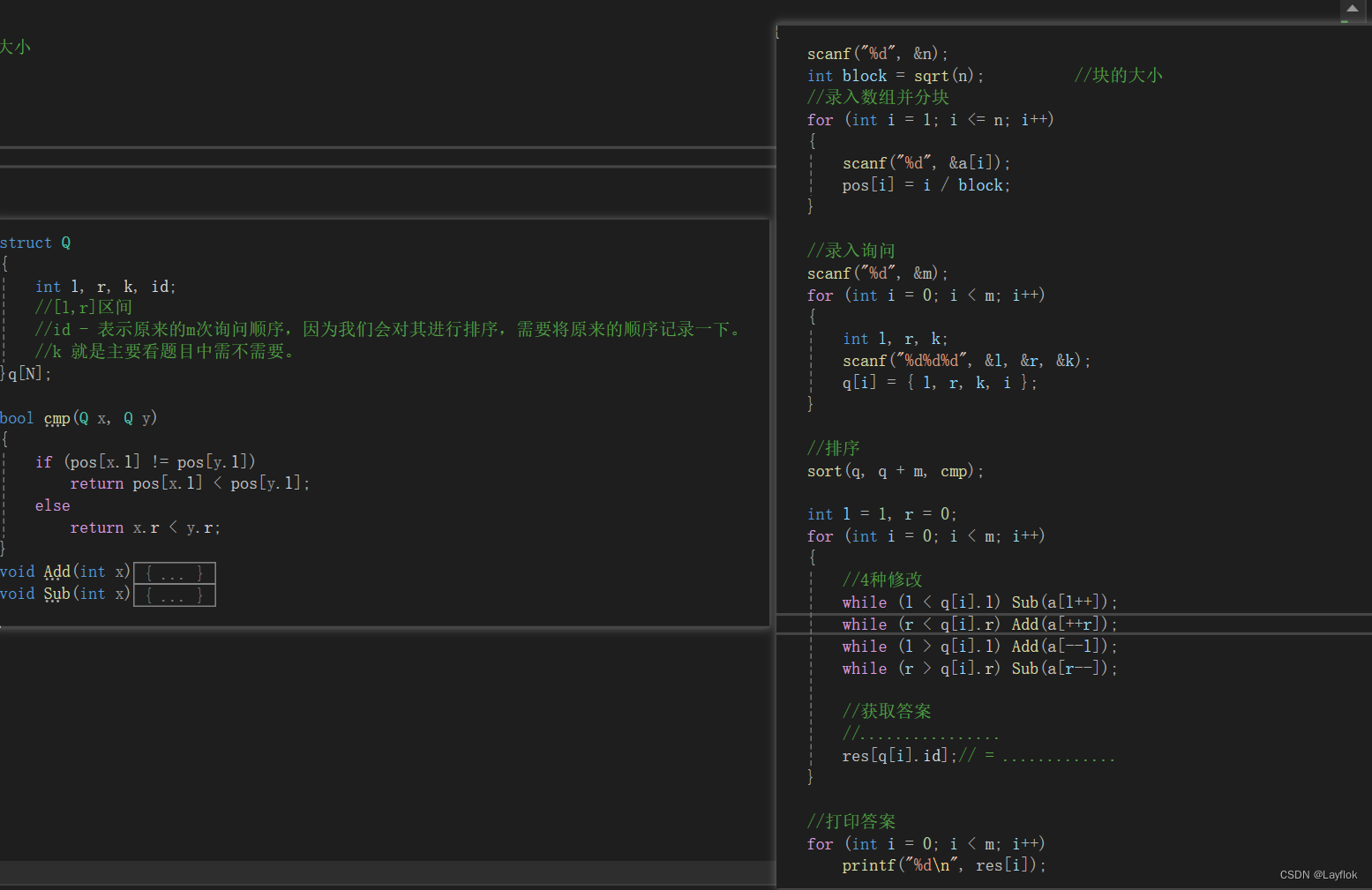
以上就是一些莫队的知识点，不是很全面，可以去别的地方学学莫队，这里就不太细说了，主要以做题为主。
而对于本题来说现在只需要设计出那两个函数就好了。
假设需要增加或者减少的数为x
h - h[x]代表数x在区间内出现了多少次。
cnt - cnt[i] 代表出现i次的数有多少个。

Add:
对x出现的次数等于i,将出现i次的个数减1。cnt[h[x]]--
将x出现的次数++；h[x]++
最后对x新出现的次数i, 将新出现的i次的个数加1.cnt[h[x]]++
Sub：
和上面的Add函数一致，只是将第二步换成了减减就好了
函数如下：

void Add(int x)
{cnt[h[x]]--;h[x]++;cnt[h[x]]++;
}
void Sub(int x)
{cnt[h[x]]--;h[x]--;cnt[h[x]]++;
}

这道题的完整代码如下：

#include <bits/stdc++.h>
using namespace std;const int N = 1e5 + 10;/*a - 原数组pos - 将数组分块h - h[i]代表数次i在区间内出现了多少次。cnt - cnt[i] 代表出现i次的数有多少个。res - 代表最后的答案
*/int n, m;
int a[N], pos[N], cnt[N], res[N], h[N];struct Q
{int l, r, k, id;//[l,r]区间//id - 表示原来的m次询问顺序，因为我们会对其进行排序，需要将原来的顺序记录一下。//k 就是主要看题目中需不需要。
}q[N];bool cmp(Q x, Q y)
{if (pos[x.l] != pos[y.l])return pos[x.l] < pos[y.l];elsereturn x.r < y.r;
}void Add(int x)
{cnt[h[x]]--;h[x]++;cnt[h[x]]++;
}
void Sub(int x)
{cnt[h[x]]--;h[x]--;cnt[h[x]]++;
}int main()
{   scanf("%d", &n);int block = sqrt(n);          //块的大小//录入数组并分块for (int i = 1; i <= n; i++){scanf("%d", &a[i]);pos[i] = i / block;}//录入询问scanf("%d", &m);for (int i = 0; i < m; i++){int l, r, k;scanf("%d%d%d", &l, &r, &k);q[i] = {l, r, k, i};}//排序sort(q, q + m, cmp);int l = 1, r = 0;for (int i = 0; i < m; i++){//4种修改while (l < q[i].l) Sub(a[l ++]);while (r < q[i].r) Add(a[++ r]);while (l > q[i].l) Add(a[-- l]);while (r > q[i].r) Sub(a[r --]);//获取答案res[q[i].id] = cnt[q[i].k];}//打印答案for (int i = 0; i < m; i++)printf("%d\n",res[i]);return 0;
}