摘要:stack OJ:最小栈、栈的弹出压入序列;queue OJ:二叉树的层序遍历(仅思路,带图解)、逆波兰表达式求值;deque,模拟实现 stack 和 queue
经过对 string、vector、list 的学习,stack 和 queue 上手起来就很快了,因此不再赘述,在使用上有疑问请查看文档。本文将会通过一些OJ题来进一步熟练 stack 和 queue.
1. stack/queue 与 vector/list
- stack/queue——容器适配器(不自己管理数据)

- vector/list——容器(自己直接管理数据)

- stack/queue 与 vector/list 的成员函数的区别:
stack/queue 没有 iterator,因为 stack 是先进后出,queue 是先进先出,不能随机遍历。
2. stack OJ
1)最小栈
155. 最小栈 - 力扣(LeetCode)
思路
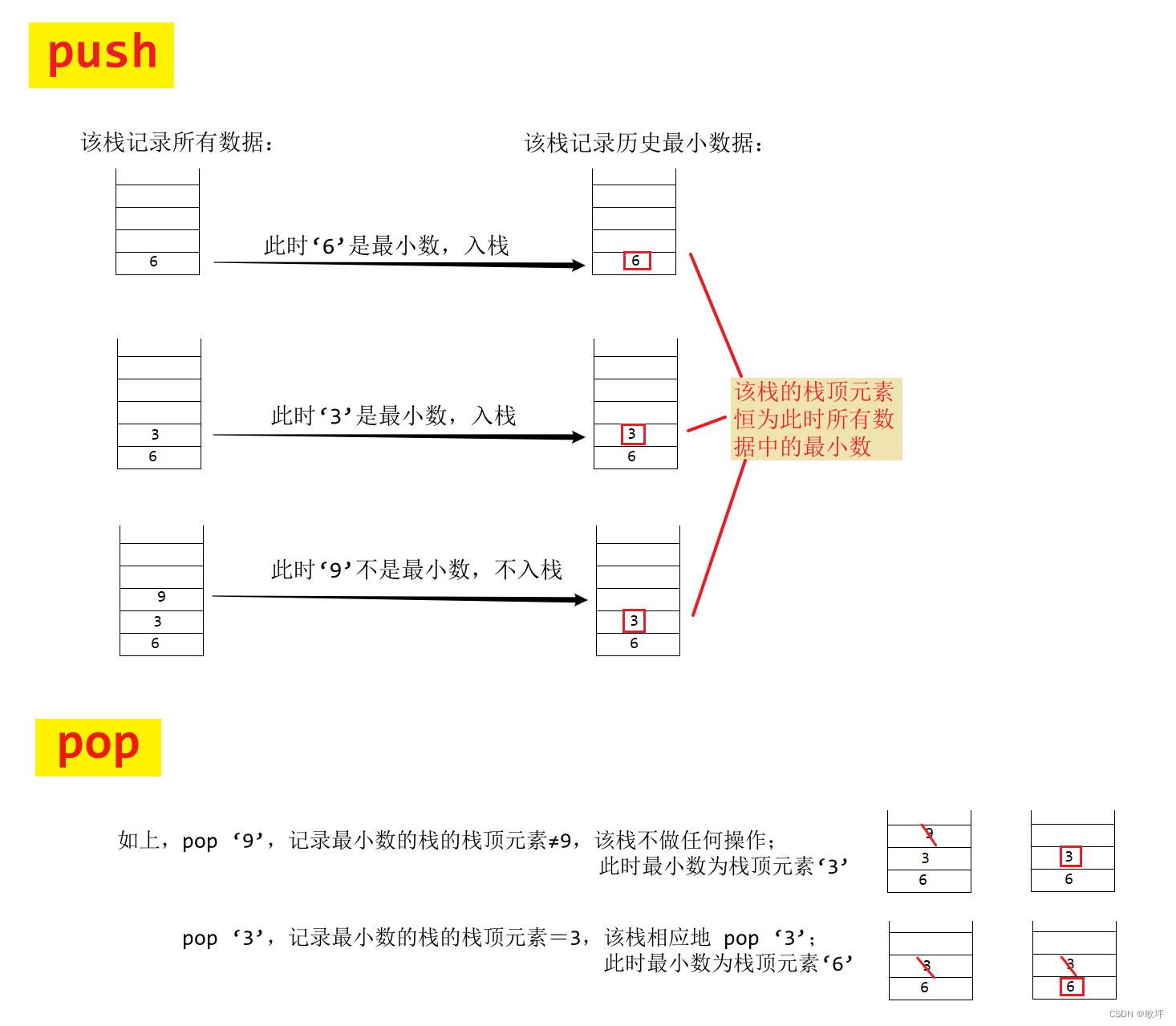
我们很容易可以想到用一个变量来存储栈中最小的数据,然而,当pop掉的数据正好是最小数时,那么这个pop操作之后的栈中的最小数就不得而知了,因此,我们不仅要记录栈中数据的当前最小数,而是要记录历史最小数。这里,我们通过使用双栈来实现这个思路。
上述思路图解示例:
代码示例
class MinStack {
public:void push(int val) {st.push(val);if(min_st.empty() || val <= min_st.top())min_st.push(val);}void pop() {if(st.top() == min_st.top()){st.pop();min_st.pop();} elsest.pop();}int top() {return st.top();}int getMin() {return min_st.top();}
private:stack<int> st;stack<int> min_st;
};/*** Your MinStack object will be instantiated and called as such:* MinStack* obj = new MinStack();* obj->push(val);* obj->pop();* int param_3 = obj->top();* int param_4 = obj->getMin();*/2)栈的压入、弹出序列
JZ31 栈的压入、弹出序列_牛客题霸_牛客网 (nowcoder.com)
思路
按给定的入栈顺序模拟数据入栈,同时按给定的出栈顺序模拟数据出栈,最终栈中数据全部出完即为该出栈顺序合法。
注意:如下图,如果先判断再入栈这个过程会比较复杂,这里建议先入栈再判断。
代码示例
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可*** @param pushV int整型vector* @param popV int整型vector* @return bool布尔型*/bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {// write code herestack<int> st;size_t size = pushV.size();for (size_t pushi = 0, popi = 0; pushi < size; ++pushi){st.push(pushV[pushi]);while (!st.empty() && st.top() == popV[popi])//要先判断是否为空才可以取top{st.pop();++popi;}}return st.empty();}
};3. queue OJ
1)二叉树的层序遍历(仅思路,带图解)
- 思路一:双队列,队列_1 用于遍历二叉树,队列_2 用于记录节点对应的层数。
如图,依次遍历,把遍历结果存储在队列中。当我们开始遍历,遍历到‘3’,记录此时层数为1;接着遍历‘3’的child节点,插入‘9’‘7’到队列中,记录此时的层数,即为上一层+1;如此循环。直到遍历完二叉树。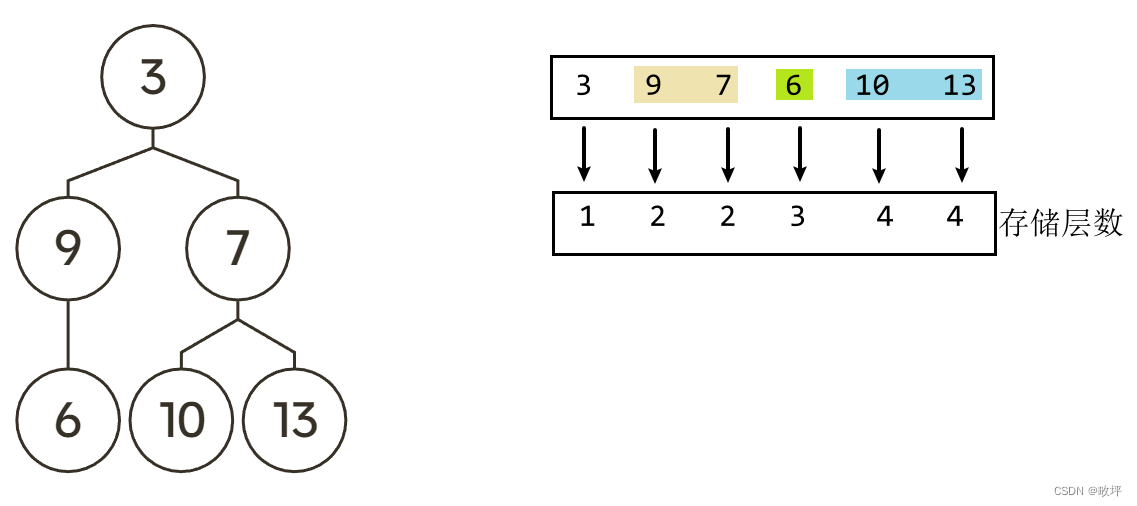
- 思路二:双队列,队列_1 用于存储 parent 节点,队列_2 用于存储 child 节点。
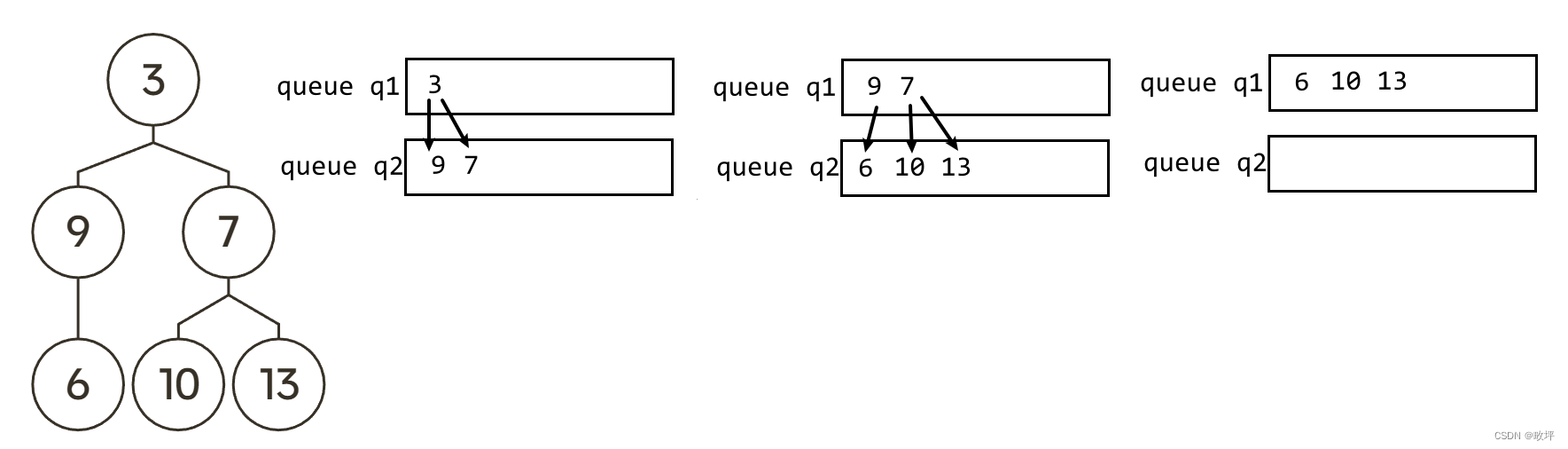
- 思路三:一个队列+一个变量,队列用于遍历二叉树,变量用于记录当前遍历到多少层。

2)逆波兰表达式求值
逆波兰表达式就是后缀表达式。逆波兰表达式求值就是后缀表达式的计算。
150. 逆波兰表达式求值 - 力扣(LeetCode)
后缀表达式的计算
- 中缀表达式:1 + 2 * 3
- 后缀表达式:1 2 3 * + (ps.后缀表达式是没有括号的,因为括号的作用是提高操作符的优先级,而后缀表达式的操作符顺序已经表现了优先级)
思路:遍历后缀表达式,遇到操作数入栈,遇到操作符就取栈顶两元素运算,运算结果再入栈,如此循环,直到遍历完后缀表达式。图例如下。

中缀表达式转后缀表达式(仅思路)
- 思路:遍历中缀表达式,遇到操作数输出;遇到操作符,如果 stack 为空,那么 push 操作符入栈,如果 stack 不为空,那么比较栈顶元素与该操作符的优先级,如果该操作符优先级更高,那么 push 操作符入栈,如果栈顶元素优先级更高或两者优先级相等,就 pop 栈顶元素。(ps.遇到括号处理成递归子问题)。
代码示例
class Solution {
public:int evalRPN(vector<string>& tokens) {stack<int> st;for(auto str:tokens){if(str == "+"||str == "-"||str == "*"||str == "/"){int right = st.top();st.pop();int left = st.top();st.pop();switch(str[0]){case '+':st.push(left + right);break;case '-':st.push(left - right);break;case '*':st.push(left * right);break;case '/':st.push(left / right);break;}}else{st.push(stoi(str));}}return st.top();}
};4. 模拟实现 stack
库里的实现 → std::stack
template <class T, class Container = deque<T> > class stack;
1)deque(简单了解)
deque 是一个结合了vector 和 list 功能的容器,但也同时结合了 vector 和 list 的双重优点和缺点。(优点多而优势不高,缺点多而缺陷不深)
deque(双端队列):是一种双开口的"连续"空间的数据结构,双开口的含义是:可以在头尾两端进行插入和删除操作,且时间复杂度为O(1),与 vector 比较,头插效率高,不需要搬移元素;与 list 比较,空间利用率比较高。

deque 和 vector 的效率比较(这个操作类似于 list 和 vector 的效率比较)
1.vector sort 的效率约为 deque 的 2倍;
2.通过把 deque 的数据拷贝到 vector 对其排序,都比直接用 deque 排序要快。(ps.通过这个操作我们可以侧面了解到数据拷贝的代价并不高)
sum.实际中 deque 并不常用,综合性比较强,但是优势又并不突出。
为什么选择deque作为stack和queue的底层默认容器:
stack是一种后进先出的特殊线性数据结构,因此只要具有 push_back() 和 pop_back() 操作的线性结构,都可 以作为stack的底层容器,比如vector 和 list 都可以;queue是 先进先出 的特殊线性数据结构,只要具有 push_back 和 pop_front 操作的线性结构,都可以作为 queue 的底层容器,比如list。但是STL中对stack和 queue 默认选择 deque 作为其底层容器,主要是因为:
- stack 和 queue 不需要遍历(因此 stack 和 queue 没有迭代器),只需要在固定的一端或者两端进行操作。
- 在 stack 中元素增长时,deque 比 vector 的效率高(扩容时不需要搬移大量数据);queue 中的元素增长 时,deque不仅效率高,而且内存使用率高。 结合了 deque 的优点,而完美的避开了其缺陷。
2)模拟实现
思路:本质就是复用别的容器的函数接口。注意后进先出的原则。
代码示例
namespace Btl
{template<class T, class Con = deque<T>>class stack{public:void push(const T& x){_c.push_back(x);}void pop(){_c.pop_back();}T& top(){return _c.back();}const T& top()const{return _c.back();}size_t size()const{return _c.size();}bool empty()const{return _c.empty();}private:Con _c;};
};5. 模拟实现 queue
同 stack,注意是先进先出的原则。
namespace Btl
{template<class T, class Con = deque<T>>class queue{public:void push(const T& x){_c.push_back(x);}void pop(){_c.pop_front();}T& back(){return _c.back();}const T& back()const{return _c.back();}T& front(){return _c.front();}const T& front()const{return _c.front();}size_t size()const{return _c.size();}bool empty()const{return _c.empty();}private:Con _c;};};END