[第1课] 均值 中位数 众数

• 均值(平均值) = 数据之和 / 数据个数
• 中位数 = 数据排序后，处在中间的数（如果两位数取平均值）
• 众数 = 出现次数最多的数,一组数据可以有多个众数

import numpy as np
import pandas as pd#定义数据
data=np.array([1,2,2,3,3,4])# 均值
print(f'mean(average) = {np.mean(data)}')# 中位数
print(f'median = {np.median(data)}')# 众数
df = pd.DataFrame(data)
print(f'mode = {df[0].mode()}')

mean(average) = 2.5
median = 2.5
mode = 0    2
1    3
dtype: int32

[第2课] 极差 中程数

• 极差 = 最大数 - 最小数
• 中程数 = 最大数和最小数的均值

import numpy as np#定义数据
data=np.array([1,2,2,3,3,4])x = np.array([np.max(data), np.min(data)])#最大数
print(f'max = {x[0]}')#最小数
print(f'min = {x[1]}')# 极差
print(f'range = {x[0]-x[1]}')
print(f'range = {np.ptp(data)}')# 中程数
print(f'midrange = {x.sum()/x.size}')
print(f'midrange = {np.mean(x)}')

max = 4
min = 1
range = 3
range = 3
midrange = 2.5
midrange = 2.5

[第3课] 象形统计图

如上图所示：
一滴血代表8个人，
O+型血有8滴，表示的人数为 $8\times 8$=64人;
O-血型人数为$8\times 2$=16人

[第4课] 条形图

本节简单不再详述

[第5课] 线形图

本节简单不再详述

[第6课] 饼图

本节简单不再详述

[第7课] 误导人的线形图

本节简单不再详述

[第8课] 茎叶图

上图是12个足球队员的各自得分，总共得多少分？
Stem：得分十位数
Leaf：得分个位数
总计得分：(0+0+2+4+7+7+9) + (11+11+11+13+18) + (20)

[第9课] 箱线图

箱式图，是指—种描述数据分布的统计图，是表述最小值、第一四分位数、中位数、第三四分位数与最大值的一种图形方法。它也可以粗略地看出数据是否具有对称性，分布的分散程度等信息[1]。

饭店老板调查了一些位顾客，他们来的地方距离饭店分别为14,6,3,2,…,10,22,20。用什么图表示这些距离的分布比较直观呢？（箱线图）

首先对这些数据进行排序，得出数据个数为17，最小值为1，最大值为22，中位数为6。

import numpy as np#定义数据
data=np.array([14,6,3,2,4,15,11,8,1,7,2,1,3,4,10,22,20])#排序
data=np.sort(data)
print(f'data = {data}')#数据个数
print(f'size = {data.size}')# 中位数
print(f'median = {np.median(data)}')

data = [ 1  1  2  2  3  3  4  4  6  7  8 10 11 14 15 20 22]
size = 17
median = 6.0

取左边8位数和右边8位数，各取中位数，作为盒子的左(2.5)、右(14)坐标画盒子；最小值(1)作为左边线的坐标点，最大值(22)作为右边线的坐标点，连上盒子；中位数(6)是盒子内部竖线坐标点。

data_left=data[0:8]
print(f'data_left = {data_left}')
print(f'median_left = {np.median(data_left)}')data_right=data[10:]
print(f'data_right = {data_right}')
print(f'median_right = {np.median(data_right)}')

data_left = [1 1 2 2 3 3 4 4]
median_left = 2.5
data_right = [ 8 10 11 14 15 20 22]
median_right = 14.0

如下图所示：

可以用Python绘制箱线图：

import numpy as np 
import matplotlib.pyplot as plt 
import pandas as pddata = np.array([14, 6, 3, 2, 4, 15, 11, 8, 1, 7, 2, 1, 3, 4, 10, 22, 20])
df = pd.DataFrame({'distance':data})
df.boxplot(patch_artist=True,showmeans=True,
)plt.show()

补充材料：

四分位数：四分位数有三个，在盒子的左右和中间位置，上图分别是$Q1=2.5$、$Q2=6$、$Q3=12.5$
四分位数的位置：
假设有n项，那么Q1位置在$\frac{n+1}{4}$、Q2位置在$\frac{n+1}{2}$、Q3位置在$\frac{3(n+1)}{4}$

如果（n+1）不为4的整数倍数，按上述分式计算出来的四分位数位置就带有小数，这时，有关的四分位数就应该是与该小数相邻的两个整数位置上的标志值的平均数，权数的大小取决于两个整数位置距离的远近，距离越近，权数越大，距离越远，权数越小,权数之和等于1。

【例】某车间某月份的工人生产某产品的数量分别为13、13.5、13.8、13.9、14、14.6、14.8、15、15.2、15.4公斤，则三个四分位数的位置分别为：

Q1 => (10+1)/4=2.75
Q2 => (10+1)/2=5.5
Q3 => 3*(10+1)/4=8.25

即变量数列中的第2.75项、第5.5项、第8.25项工人的某种产品产量分别为下四分位数、中位数和上四分位数。即：

Q1 = 0.25*第二项 + 0.75*第三项 = 13.75

参考:https://blog.csdn.net/kevinelstri/article/details/52937236

[第10课] 箱线图2

上图是100棵树的树龄箱线图，问树龄极差是多少，树龄中位数是多少？

由图可以看出：最小值是8，最大值是50，所以极差是50-8=42；中位数就是盒子里的竖线坐标21。

[第11课] 统计：集中趋势

集中趋势 (central tendency) 又称“数据的中心位置”，再次介绍了均值，中位数和众数。见第1课

[第12课] 统计：样本和总体

提出样本和总体的概念。比如求美国所有男性的平均身高，可以抽取部分样本数据计算平均值$\overline{X}=\frac{\sum _{i=1}^N{x}_i}{N}=\frac{x_1+x_2+...+x_N}{N}$，一定程度上代表了总体均值$\mu$。

$\sum$读作sum

[第13课] 统计：总体方差

方差（variance）用来描述数据和均值之间的偏离程度 。${\sigma }^2$ 读作 sigma square

方差公式：${\sigma }^2=\frac{\sum _{i=1}^N(x_i-\mu {)}^2}{N}$

例如数据 1,2,3,4, 平均值是$\frac{1+2+3}{3}=2$,总体方差是$\frac{(1-2{)}^2+(2-2{)}^2+(3-2{)}^2}{3}=\frac{2}{3}=0.666...$

import numpy as np#定义数据
data=np.array([1,2,3])# 均值
print(f'mean(average) = {np.mean(data)}')# 方差
print(f'variance = {np.var(data)}')

mean(average) = 2.0
variance = 0.6666666666666666

[第14课] 统计：样本方差

样本方差跟总体方差公式不一样：$S^2=\frac{\sum _{i=1}^n(x_i-\overline{X}{)}^2}{n-1}$ 注意是n-1而不是n。 详见《彻底理解样本方差为何除以n-1》

例如数据 1,2,3,4, 平均值是$\frac{1+2+3}{3}=2$,样本方差是$\frac{(1-2{)}^2+(2-2{)}^2+(3-2{)}^2}{3-1}=\frac{2}{3-1}=1$

import numpy as np#定义数据
data=np.array([1,2,3])# 均值
print(f'mean(average) = {np.mean(data)}')# 样本方差
print(f'sample variance = {np.var(data,ddof=1)}')

mean(average) = 2.0
sample variance = 1.0

[第15课] 统计：标准差

标准差 (standard deviation)是表述数据和均值之间的偏离程度的另一个重要标志。它等于方差的平方根。
标准差公式：$\sigma =\sqrt{{\sigma }^2}$
样本标准差公式：$S=\sqrt{S^2}$

import numpy as np#定义数据
data=np.array([1,2,3])# 方差
print(f'variance = {np.var(data)}')
# 标准差
print(f'standard deviation = {np.std(data)}')# 样本方差
print(f'sample variance = {np.var(data,ddof=1)}')
# 标准差
print(f'sample standard deviation = {np.std(data,ddof=1)}')

variance = 0.6666666666666666
standard deviation = 0.816496580927726
sample variance = 1.0
sample standard deviation = 1.0

[第16课] 统计：诸方差公式

本节课，可汗老师对原始方差公式进行推导，得出如下更简洁的公式。

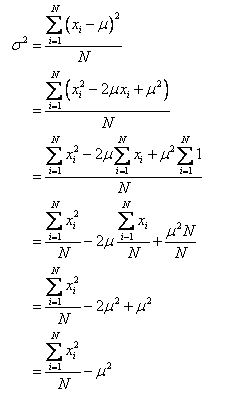
主要参考资料：

主要参考资料：
视频：《可汗学院统计学》
文章：csdn shangboerds 学习笔记
Jent’s Blog 学习笔记（后来发现的，写得很好，推荐）