目录
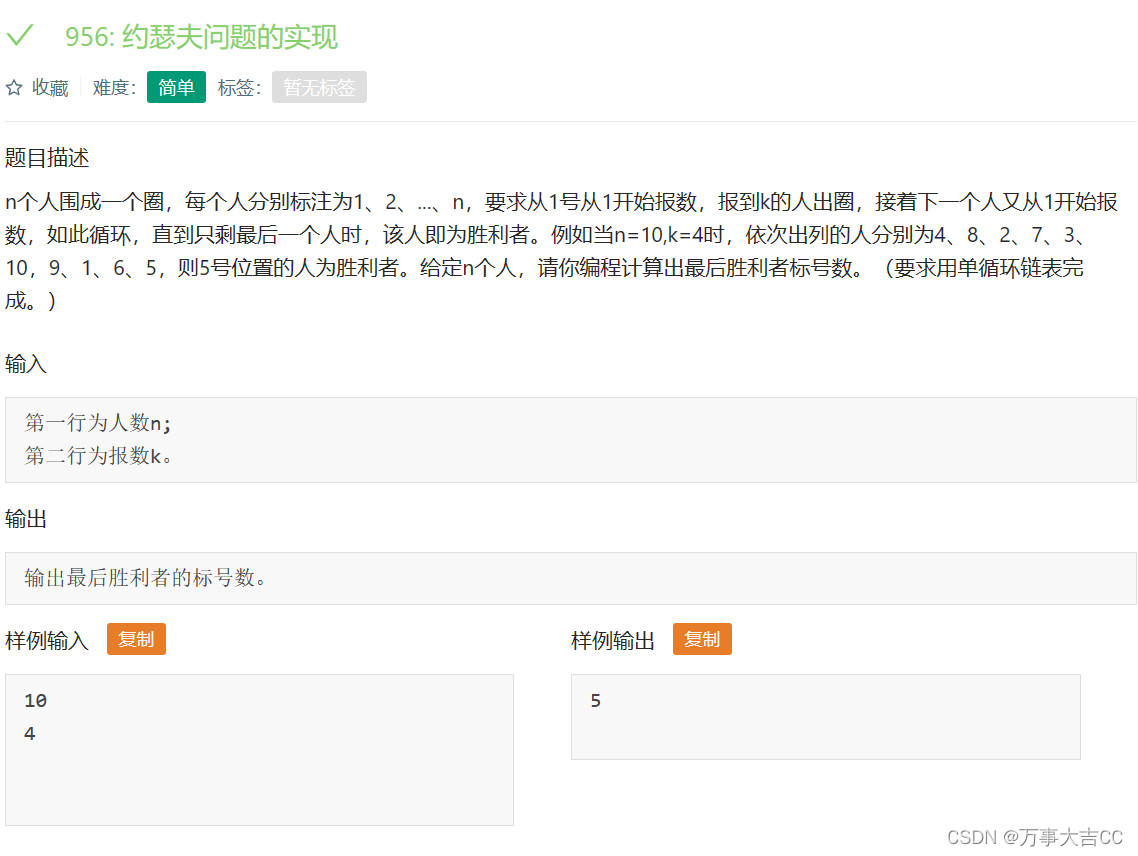
题目描述:
思路描述:
代码:
纯递归:
带有记忆化搜索的递归:
题目描述:
给你一个下标从 0 开始、大小为 m x n 的矩阵 grid ,矩阵由若干 正 整数组成。
你可以从矩阵第一列中的 任一 单元格出发,按以下方式遍历 grid :
- 从单元格
(row, col)可以移动到(row - 1, col + 1)、(row, col + 1)和(row + 1, col + 1)三个单元格中任一满足值 严格 大于当前单元格的单元格。
返回你在矩阵中能够 移动 的 最大 次数。
示例 1:
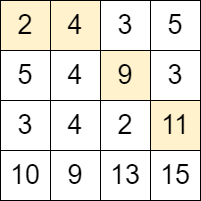
输入:grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]] 输出:3 解释:可以从单元格 (0, 0) 开始并且按下面的路径移动: - (0, 0) -> (0, 1). - (0, 1) -> (1, 2). - (1, 2) -> (2, 3). 可以证明这是能够移动的最大次数。
示例 2:
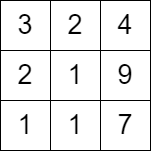
输入:grid = [[3,2,4],[2,1,9],[1,1,7]] 输出:0 解释:从第一列的任一单元格开始都无法移动。
提示:
m == grid.lengthn == grid[i].length2 <= m, n <= 10004 <= m * n <= 10^51 <= grid[i][j] <= 10^6
思路描述:
从第一列开始进行有条件的深度优先搜索即可,如果纯递归的话,会超时。
递归加上记忆化搜索,既可以以比较好的时间复杂度通过了。
代码:
纯递归:
public class Solation{/*** 从单元格 (row, col) 可以移动到 (row - 1, col + 1)、(row, col + 1) 和 (row + 1, col + 1) 三个单元格中任一满足值 严格 大于当前单元格的单元格。* 返回你在矩阵中能够 移动 的 最大 次数。*/int[][] direction={{-1,1},{0,1},{1,1}};int MaxStep=Integer.MIN_VALUE;public int maxMoves(int[][] grid) {for(int i=0;i<grid.length;i++){myfun(grid,i,0,0);}return MaxStep;}public void myfun(int[][] grid,int row,int col,int step){if(step>=grid[0].length){MaxStep=Math.max(step,MaxStep);return;}boolean flag=false;for(int i=0;i<direction.length;i++){if(row+direction[i][0]<grid.length &&col+direction[i][1]<grid[0].length && row+direction[i][0]>=0 &&row+direction[i][1]>=0 && grid[row][col]<grid[row+direction[i][0]][col+direction[i][1]]){flag=true;myfun(grid,row+direction[i][0],col+direction[i][1],step+1);}}if(!flag){MaxStep=Math.max(step,MaxStep);}}
}
带有记忆化搜索的递归:
class Solution {int m;int n;int[][] direction = new int[][]{{-1, 1}, {0, 1}, {1, 1}};public int maxMoves(int[][] grid) {m = grid.length;n = grid[0].length;int[][] dis = new int[m][n];for(int i = 0; i < m; i++){Arrays.fill(dis[i], -1);}int result = 0;for(int i = 0; i < m; i++){result = Math.max(result, findPath(i, 0, grid, dis) );}return result;}private int findPath(int x, int y, int[][] grid, int[][] dis){if(dis[x][y] != -1){return dis[x][y];}int maxLength = 0;for(int i = 0; i < 3; i++){int new_x = x + direction[i][0];int new_y = y + direction[i][1];if(new_x >= 0 && new_x < m && new_y < n && grid[new_x][new_y] > grid[x][y]){maxLength = Math.max(maxLength, findPath(new_x, new_y, grid, dis) + 1);}}dis[x][y] = maxLength;return dis[x][y];}
}