深度学习笔记完整教程(附代码资料)主要内容讲述:深度学习课程,深度学习介绍要求,目标,学习目标,1.1.1 区别,学习目标,学习目标。TensorFlow介绍,2.4 张量学习目标,2.4.1 张量(Tensor),2.4.2 创建张量的指令,2.4.3 张量的变换,2.4.4 张量的数学运算,学习目标。TensorFlow介绍,1.2 神经网络基础学习目标。TensorFlow介绍,总结学习目标,1.3.1 神经网络,1.3.2 playground使用,学习目标,1.4.1 softmax回归,1.4.2 交叉熵损失。神经网络与tf.keras,1.3 Tensorflow实现神经网络学习目标,1.3.1 TensorFlow keras介绍,1.3.2 案例:实现多层神经网络进行时装分类。神经网络与tf.keras,1.4 深层神经网络学习目标。卷积神经网络,3.1 卷积神经网络(CNN)原理学习目标。卷积神经网络,3.1 卷积神经网络(CNN)原理学习目标。卷积神经网络,2.2案例:CIFAR100类别分类学习目标,2.2.1 CIFAR100数据集介绍,2.2.2 API 使用,2.2.3 步骤分析以及代码实现(缩减版LeNet5),学习目标。卷积神经网络,2.4 BN与神经网络调优学习目标。卷积神经网络,2.4 经典分类网络结构学习目标,2.4.6 案例:使用pre_trained模型进行VGG预测,2.4.7 总结。卷积神经网络,2.5 CNN网络实战技巧学习目标,3.1.1 案例:基于VGG对五种图片类别识别的迁移学习,3.1.2 数据增强的作用。卷积神经网络,总结学习目标,1.1.1 项目演示,1.1.2 项目结构,1.1.3 项目知识点,学习目标,1.2.1 安装。商品物体检测项目介绍,3.4 Fast R-CNN。YOLO与SSD,4.3 案例:SSD进行物体检测4.3.1 案例效果,4.3.2 案例需求,4.3.3 步骤分析以及代码,2.1.1 常用目标检测数据集,2.1.2 pascal voc数据集介绍,2.1.3 XML。商品检测数据集训练,5.2 标注数据读取与存储5.2.1 案例:xml读取本地文件存储到pkl,5.3.1 案例训练结果,5.3.2 案例思路,5.3.3 多GPU训练代码修改,5.4.1 预测代码,5.4.1 keras 模型进行TensorFlow导出。
全套笔记资料代码移步: 前往gitee仓库查看
感兴趣的小伙伴可以自取哦,欢迎大家点赞转发~
全套教程部分目录:


部分文件图片:
TensorFlow介绍
说明TensorFlow的数据流图结构
应用TensorFlow操作图
说明会话在TensorFlow程序中的作用
应用TensorFlow实现张量的创建、形状类型修改操作
应用Variable实现变量op的创建
应用Tensorboard实现图结构以及张量值的显示
应用tf.train.saver实现TensorFlow的模型保存以及加载
应用tf.app.flags实现命令行参数添加和使用
应用TensorFlow实现线性回归
1.2 神经网络基础
学习目标
-
目标
-
知道逻辑回归的算法计算输出、损失函数
- 知道导数的计算图
- 知道逻辑回归的梯度下降算法
-
知道多样本的向量计算
-
应用
-
应用完成向量化运算
- 应用完成一个单神经元神经网络的结构
1.2.1 Logistic回归
1.2.1.1 Logistic回归
逻辑回归是一个主要用于二分分类类的算法。那么逻辑回归是给定一个 x x x, 输出一个该样本属于1对应类别的预测概率 y ^ = P ( y = 1 ∣ x ) \hat{y}=P(y=1|x) y^=P(y=1∣x)。
Logistic 回归中使用的参数如下:


e − z e^{-z} e−z的函数如下
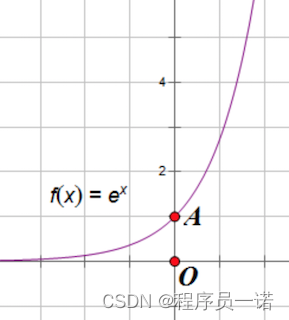
例如:
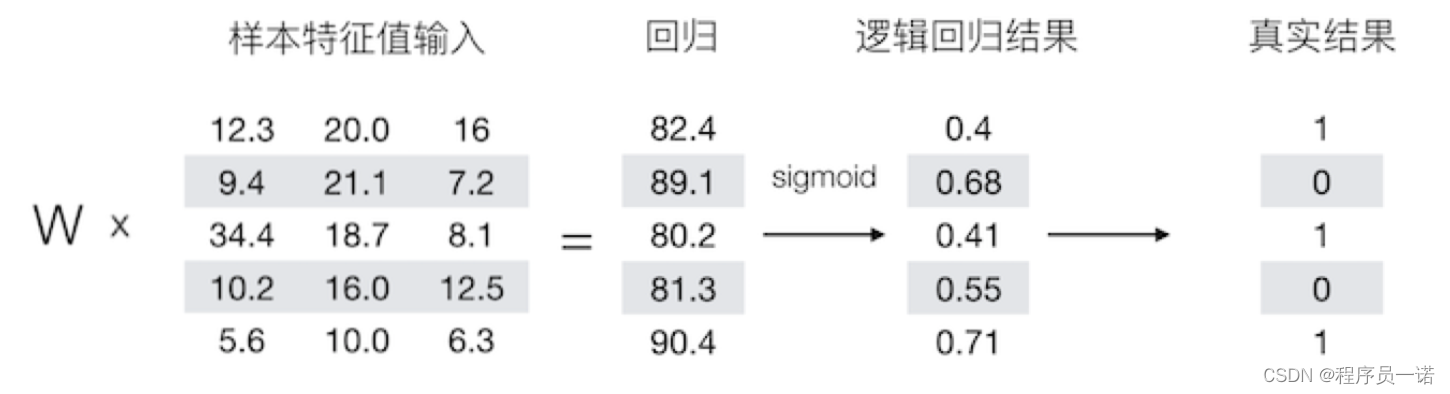
1.2.1.2 逻辑回归损失函数
损失函数(loss function)用于衡量预测结果与真实值之间的误差。最简单的损失函数定义方式为平方差损失:
L ( y ^ , y ) = 1 2 ( y ^ − y ) 2 L(\hat{y},y) = \frac{1}{2}(\hat{y}-y)^2 L(y^,y)=21(y^−y)2
逻辑回归一般使用 L ( y ^ , y ) = − ( y log y ^ ) − ( 1 − y ) log ( 1 − y ^ ) L(\hat{y},y) = -(y\log\hat{y})-(1-y)\log(1-\hat{y}) L(y^,y)=−(ylogy^)−(1−y)log(1−y^)
该式子的理解:
- 如果y=1,损失为 − log y ^ - \log\hat{y} −logy^,那么要想损失越小, y ^ \hat{y} y^的值必须越大,即越趋近于或者等于1
- 如果y=0,损失为 1 log ( 1 − y ^ ) 1\log(1-\hat{y}) 1log(1−y^),那么要想损失越小,那么 y ^ \hat{y} y^的值越小,即趋近于或者等于0
损失函数是在单个训练样本中定义的,它衡量了在单个训练样本上的表现。代价函数(cost function)衡量的是在全体训练样本上的表现,即衡量参数 w 和 b 的效果,所有训练样本的损失平均值
J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) J(w,b) = \frac{1}{m}\sum_{i=1}^mL(\hat{y}^{(i)},y^{(i)}) J(w,b)=m1∑i=1mL(y^(i),y(i))
1.2.2 梯度下降算法
目的:使损失函数的值找到最小值
方式:梯度下降
函数的梯度(gradient)指出了函数的最陡增长方向。梯度的方向走,函数增长得就越快。那么按梯度的负方向走,函数值自然就降低得最快了。模型的训练目标即是寻找合适的 w 与 b 以最小化代价函数值。假设 w 与 b 都是一维实数,那么可以得到如下的 J 关于 w 与 b 的图:
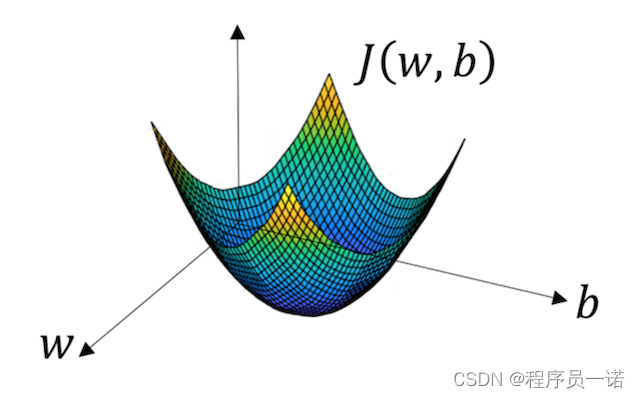
可以看到,成本函数 J 是一个凸函数,与非凸函数的区别在于其不含有多个局部最低。
参数w和b的更新公式为:
w : = w − α d J ( w , b ) d w w := w - \alpha\frac{dJ(w, b)}{dw} w:=w−αdwdJ(w,b), b : = b − α d J ( w , b ) d b b := b - \alpha\frac{dJ(w, b)}{db} b:=b−αdbdJ(w,b)
注:其中 α 表示学习速率,即每次更新的 w 的步伐长度。当 w 大于最优解 w′ 时,导数大于 0,那么 w 就会向更小的方向更新。反之当 w 小于最优解 w′ 时,导数小于 0,那么 w 就会向更大的方向更新。迭代直到收敛。
通过平面来理解梯度下降过程:
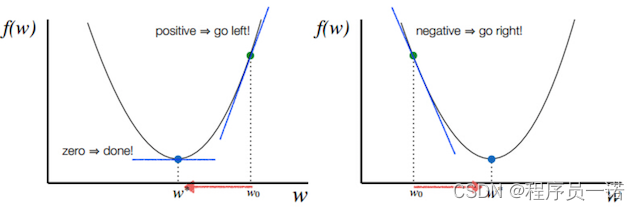
1.2.3 导数
理解梯度下降的过程之后,我们通过例子来说明梯度下降在计算导数意义或者说这个导数的意义。
1.2.3.1 导数
导数也可以理解成某一点处的斜率。斜率这个词更直观一些。
- 各点处的导数值一样
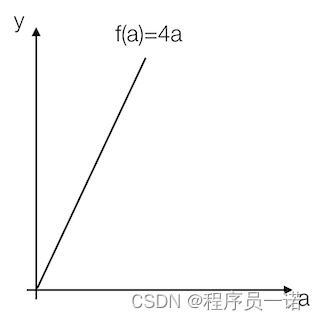
我们看到这里有一条直线,这条直线的斜率为4。我们来计算一个例子
例:取一点为a=2,那么y的值为8,我们稍微增加a的值为a=2.001,那么y的值为8.004,也就是当a增加了0.001,随后y增加了0.004,即4倍
那么我们的这个斜率可以理解为当一个点偏移一个不可估量的小的值,所增加的为4倍。
可以记做 f ( a ) d a \frac{f(a)}{da} daf(a)或者 d d a f ( a ) \frac{d}{da}f(a) dadf(a)
- 各点的导数值不全一致
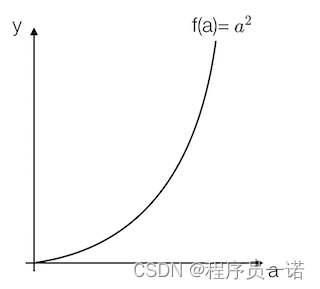
例:取一点为a=2,那么y的值为4,我们稍微增加a的值为a=2.001,那么y的值约等于4.004(4.004001),也就是当a增加了0.001,随后y增加了4倍
取一点为a=5,那么y的值为25,我们稍微增加a的值为a=5.001,那么y的值约等于25.01(25.010001),也就是当a增加了0.001,随后y增加了10倍
可以得出该函数的导数2为2a。
- 更多函数的导数结果
| 函数 | 导数 |
|---|---|
| f(a)=a2f(a) = a^2f(a)=a2 | 2a2a2a |
| f(a)=a3f(a)=a^3f(a)=a3 | 3a23a^23a2 |
| f(a)=ln(a)f(a)=ln(a)f(a)=ln(a) | 1a\frac{1}{a}a1 |
| f(a)=eaf(a) = e^af(a)=ea | eae^aea |
| σ(z)=11+e−z\sigma(z) = \frac{1}{1+e^{-z}}σ(z)=1+e−z1 | σ(z)(1−σ(z))\sigma(z)(1-\sigma(z))σ(z)(1−σ(z)) |
| g(z)=tanh(z)=ez−e−zez+e−zg(z) = tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}g(z)=tanh(z)=ez+e−zez−e−z | 1−(tanh(z))2=1−(g(z))21-(tanh(z))^2=1-(g(z))^21−(tanh(z))2=1−(g(z))2 |
1.2.3.2 导数计算图
那么接下来我们来看看含有多个变量的到导数流程图,假设 J ( a , b , c ) = 3 ( a + b c ) J(a,b,c) = 3{(a + bc)} J(a,b,c)=3(a+bc)
我们以下面的流程图代替
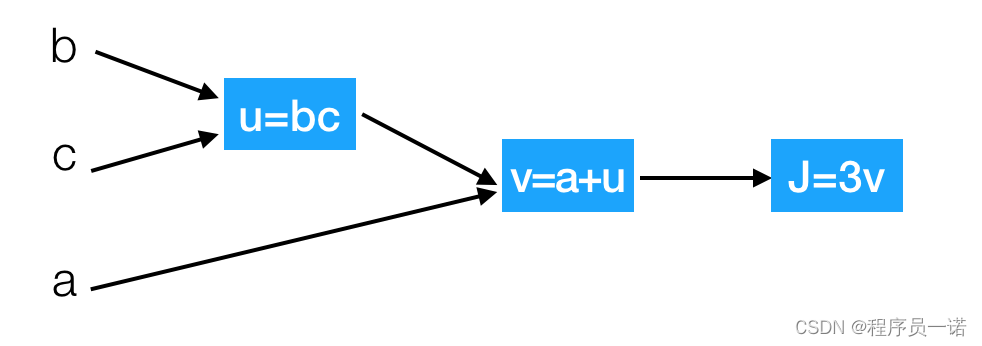
这样就相当于从左到右计算出结果,然后从后往前计算出导数
- 导数计算
问题:那么现在我们要计算J相对于三个变量a,b,c的导数?
假设b=4,c=2,a=7,u=8,v=15,j=45
- d J d v = 3 \frac{dJ}{dv}=3 dvdJ=3
增加v从15到15.001,那么 J ≈ 4 5 . 0 0 3 J\approx45.003 J≈45.003
- d J d a = 3 \frac{dJ}{da}=3 dadJ=3
增加a从7到7.001,那么 v = ≈ 1 5 . 0 0 1 v=\approx15.001 v=≈15.001, J ≈ 4 5 . 0 0 3 J\approx45.003 J≈45.003
这里也涉及到链式法则
1.2.3.3 链式法则
- d J d a = d J d v d v d a = 3 ∗ 1 = 3 \frac{dJ}{da}=\frac{dJ}{dv}\frac{dv}{da}=3*1=3 dadJ=dvdJdadv=3∗1=3
J相对于a增加的量可以理解为J相对于v*v相对于a增加的
接下来计算
-
d J d b = 6 = d J d u d u d b = 3 ∗ 2 \frac{dJ}{db}=6=\frac{dJ}{du}\frac{du}{db}=3*2 dbdJ=6=dudJdbdu=3∗2
-
d J d c = 9 = d J d u d u d c = 3 ∗ 3 \frac{dJ}{dc}=9=\frac{dJ}{du}\frac{du}{dc}=3*3 dcdJ=9=dudJdcdu=3∗3
1.2.3.4 逻辑回归的梯度下降
逻辑回归的梯度下降过程计算图,首先从前往后的计算图得出如下
-
z = w T x + b z = w^Tx + b z=wTx+b
-
y ^ = a = σ ( z ) \hat{y} =a= \sigma(z) y^=a=σ(z)
-
L ( y ^ , y ) = − ( y log a ) − ( 1 − y ) log ( 1 − a ) L(\hat{y},y) = -(y\log{a})-(1-y)\log(1-a) L(y^,y)=−(yloga)−(1−y)log(1−a)
那么计算图从前向过程为,假设样本有两个特征
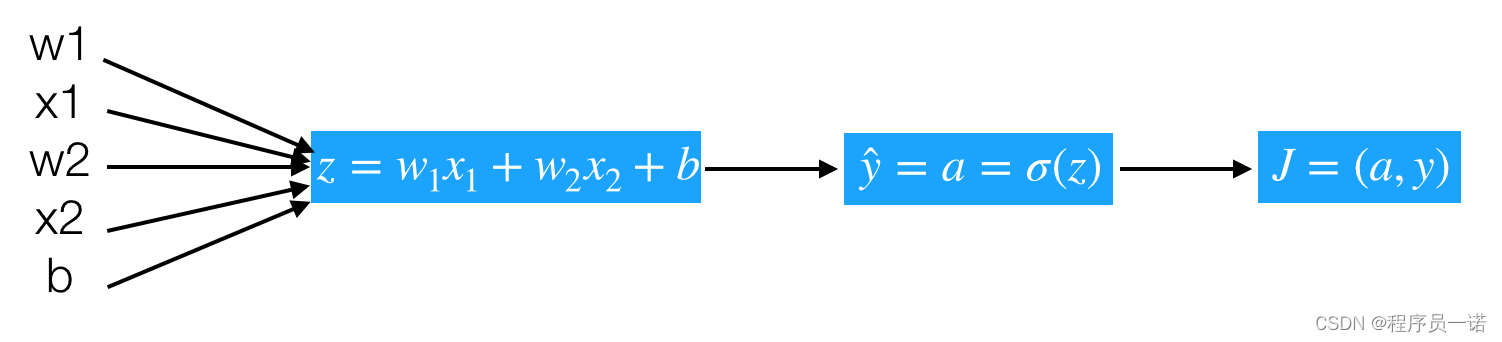
问题:计算出 J J J关于 z z z的导数
- d z = d J d a d a d z = a − y dz = \frac{dJ}{da}\frac{da}{dz} = a-y dz=dadJdzda=a−y
- d J d a = − y a + 1 − y 1 − a \frac{dJ}{da} = -\frac{y}{a} + \frac{1-y}{1-a} dadJ=−ay+1−a1−y
- d a d z = a ( 1 − a ) \frac{da}{dz} = a(1-a) dzda=a(1−a)
所以我们这样可以求出总损失相对于 w 1 , w 2 , b w_1,w_2,b w1,w2,b参数的某一点导数,从而可以更新参数
- d J d w 1 = d J d z d z d w 1 = d z ∗ x 1 \frac{dJ}{dw_1} = \frac{dJ}{dz}\frac{dz}{dw_1}=dz*x1 dw1dJ=dzdJdw1dz=dz∗x1
- d J d w 2 = d J d z d z d w 1 = d z ∗ x 2 \frac{dJ}{dw_2} = \frac{dJ}{dz}\frac{dz}{dw_1}=dz*x2 dw2dJ=dzdJdw1dz=dz∗x2
- d J d b = d z \frac{dJ}{db}=dz dbdJ=dz
相信上面的导数计算应该都能理解了,所以当我们计算损失函数的某个点相对于 w 1 , w 2 , b w_1,w_2,b w1,w2,b的导数之后,就可以更新这次优化后的结果。
w 1 : = w 1 − α d J ( w 1 , b ) d w 1 w_1 := w_1 - \alpha\frac{dJ(w_1, b)}{dw_1} w1:=w1−αdw1dJ(w1,b)
w 2 : = w 2 − α d J ( w 2 , b ) d w 2 w_2 := w_2 - \alpha\frac{dJ(w_2, b)}{dw_2} w2:=w2−αdw2dJ(w2,b)
b : = b − α d J ( w , b ) d b b := b - \alpha\frac{dJ(w, b)}{db} b:=b−αdbdJ(w,b)
1.2.4 向量化编程
每更新一次梯度时候,在训练期间我们会拥有m个样本,那么这样每个样本提供进去都可以做一个梯度下降计算。所以我们要去做在所有样本上的计算结果、梯度等操作
J ( w , b ) = 1 m ∑ i = 1 m L ( a ( i ) , y ( i ) ) J(w,b) = \frac{1}{m}\sum_{i=1}^mL({a}^{(i)},y^{(i)}) J(w,b)=m1∑i=1mL(a(i),y(i))
计算参数的梯度为:这样,我们想要得到最终的 d w 1 , d w 2 , d b d{w_1},d{w_2},d{b} dw1,dw2,db,如何去设计一个算法计算?伪代码实现:

1.2.4.1 向量化优势
什么是向量化
由于在进行计算的时候,最好不要使用for循环去进行计算,因为有Numpy可以进行更加快速的向量化计算。
在公式 z = w T x + b z = w^Tx+b z=wTx+b中 w , x w,x w,x都可能是多个值,也就是

import numpy as np
import time
a = np.random.rand(100000)
b = np.random.rand(100000)
- 第一种方法
# 第一种for 循环c = 0
start = time.time()
for i in range(100000):c += a[i]*b[i]
end = time.time()print("计算所用时间%s " % str(1000*(end-start)) + "ms")
- 第二种向量化方式使用np.dot
# 向量化运算start = time.time()
c = np.dot(a, b)
end = time.time()
print("计算所用时间%s " % str(1000*(end-start)) + "ms")
Numpy能够充分的利用并行化,Numpy当中提供了很多函数使用
| 函数 | 作用 |
|---|---|
| np.ones or np.zeros | 全为1或者0的矩阵 |
| np.exp | 指数计算 |
| np.log | 对数计算 |
| np.abs | 绝对值计算 |
所以上述的m个样本的梯度更新过程,就是去除掉for循环。原本这样的计算
1.2.4.2 向量化实现伪代码
- 思路
| z1=wTx1+bz^1 = w^Tx^1+bz1=wTx1+b | z2=wTx2+bz^2 = w^Tx^2+bz2=wTx2+b | z3=wTx3+bz^3 = w^Tx^3+bz3=wTx3+b |
|---|---|---|
| a1=σ(z1)a^1 = \sigma(z^1)a1=σ(z1) | a2=σ(z2)a^2 = \sigma(z^2)a2=σ(z2) | a3=σ(z3)a^3 = \sigma(z^3)a3=σ(z3) |
可以变成这样的计算
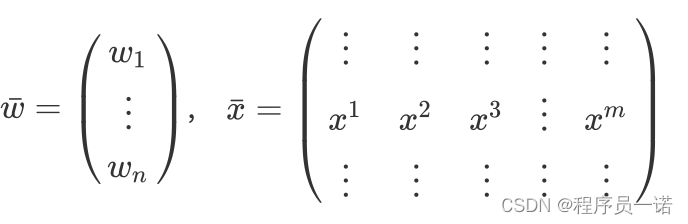
注:w的形状为(n,1), x的形状为(n, m),其中n为特征数量,m为样本数量
我们可以让,得出的结果为(1, m)大小的矩阵 注:大写的wx为多个样本表示
- 实现多个样本向量化计算的伪代码

这相当于一次使用了M个样本的所有特征值与目标值,那我们知道如果想多次迭代,使得这M个样本重复若干次计算
1.2.5 案例:实现逻辑回归
1.2.5.1使用数据:制作二分类数据集
from sklearn.datasets import load_iris, make_classification
from sklearn.model_selection import train_test_split
import tensorflow as tf
import numpy as npX, Y = make_classification(n_samples=500, n_features=5, n_classes=2)
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.3)
1.2.5.2 步骤设计:
分别构建算法的不同模块
- 1、初始化参数
def initialize_with_zeros(shape):"""创建一个形状为 (shape, 1) 的w参数和b=0.return:w, b"""w = np.zeros((shape, 1))b = 0return w, b
-
计算成本函数及其梯度
-
w (n,1).T * x (n, m)
- y: (1, n)
def propagate(w, b, X, Y):"""参数:w,b,X,Y:网络参数和数据Return:损失cost、参数W的梯度dw、参数b的梯度db"""m = X.shape[1]# w (n,1), x (n, m)A = basic_sigmoid(np.dot(w.T, X) + b)# 计算损失cost = -1 / m * np.sum(Y * np.log(A) + (1 - Y) * np.log(1 - A))dz = A - Ydw = 1 / m * np.dot(X, dz.T)db = 1 / m * np.sum(dz)cost = np.squeeze(cost)grads = {"dw": dw,"db": db}return grads, cost
需要一个基础函数sigmoid
def basic_sigmoid(x):"""计算sigmoid函数"""s = 1 / (1 + np.exp(-x))return s
-
使用优化算法(梯度下降)
-
实现优化函数. 全局的参数随着w,b对损失J进行优化改变. 对参数进行梯度下降公式计算,指定学习率和步长。
-
循环:
- 计算当前损失
- 计算当前梯度
- 更新参数(梯度下降)
def optimize(w, b, X, Y, num_iterations, learning_rate):"""参数:w:权重,b:偏置,X特征,Y目标值,num_iterations总迭代次数,learning_rate学习率Returns:params:更新后的参数字典grads:梯度costs:损失结果"""costs = []for i in range(num_iterations):# 梯度更新计算函数grads, cost = propagate(w, b, X, Y)# 取出两个部分参数的梯度dw = grads['dw']db = grads['db']# 按照梯度下降公式去计算w = w - learning_rate * dwb = b - learning_rate * dbif i % 100 == 0:costs.append(cost)if i % 100 == 0:print("损失结果 %i: %f" %(i, cost))print(b)params = {"w": w,"b": b}grads = {"dw": dw,"db": db}return params, grads, costs
- 预测函数(不用实现)
利用得出的参数来进行测试得出准确率
def predict(w, b, X):'''利用训练好的参数预测return:预测结果'''m = X.shape[1]y_prediction = np.zeros((1, m))w = w.reshape(X.shape[0], 1)# 计算结果A = basic_sigmoid(np.dot(w.T, X) + b)for i in range(A.shape[1]):if A[0, i] <= 0.5:y_prediction[0, i] = 0else:y_prediction[0, i] = 1return y_prediction
-
整体逻辑
-
模型训练
def model(x_train, y_train, x_test, y_test, num_iterations=2000, learning_rate=0.0001):""""""# 修改数据形状x_train = x_train.reshape(-1, x_train.shape[0])x_test = x_test.reshape(-1, x_test.shape[0])y_train = y_train.reshape(1, y_train.shape[0])y_test = y_test.reshape(1, y_test.shape[0])print(x_train.shape)print(x_test.shape)print(y_train.shape)print(y_test.shape)# 1、初始化参数w, b = initialize_with_zeros(x_train.shape[0])# 2、梯度下降# params:更新后的网络参数# grads:最后一次梯度# costs:每次更新的损失列表params, grads, costs = optimize(w, b, x_train, y_train, num_iterations, learning_rate)# 获取训练的参数# 预测结果w = params['w']b = params['b']y_prediction_train = predict(w, b, x_train)y_prediction_test = predict(w, b, x_test)# 打印准确率print("训练集准确率: {} ".format(100 - np.mean(np.abs(y_prediction_train - y_train)) * 100))print("测试集准确率: {} ".format(100 - np.mean(np.abs(y_prediction_test - y_test)) * 100))return None
- 训练
model(x_train, y_train, x_test, y_test, num_iterations=2000, learning_rate=0.0001)