Bayesian Optimization(贝叶斯优化)是一种用于超参数调优的技术,对于类似随机森林(Random Forest,简称RF)的机器学习算法非常重要。随机森林是一种集成学习方法,它在训练过程中构建多个决策树,并输出这些树的类别众数(分类问题)或平均预测值(回归问题)。
以下是贝叶斯优化如何应用于优化随机森林分类器的原理:
-
定义超参数空间:首先要定义超参数空间。对于随机森林,常见的超参数包括森林中树的数量、树的最大深度、分裂节点所需的最小样本数等。
-
选择目标函数:定义一个目标函数,该函数以超参数作为输入,并返回您想要优化的性能指标。这可以是准确率、精确率、召回率、F1分数等,具体取决于手头的问题。
-
初始化贝叶斯优化:贝叶斯优化通常从一组初始超参数开始,这些超参数可以是随机选择的,也可以基于一些启发式方法选择。这些初始超参数用于评估目标函数。
-
构建代理模型:贝叶斯优化依赖于构建目标函数的代理模型。高斯过程(Gaussian Process,简称GP)回归通常用于此目的。GP回归提供了目标函数的概率模型。
-
更新模型:在每次迭代中,贝叶斯优化使用已知的超参数和对应的目标函数值来更新代理模型。这样,模型就能够更好地预测目标函数在未知超参数处的表现。
-
选择下一个超参数:基于代理模型的预测,贝叶斯优化选择下一个最有可能优化目标函数的超参数。通常采用的方法是根据不确定性来进行探索-开发权衡,即在已知最佳性能的区域附近进行开发,同时在不确定性高的区域进行探索。
-
评估目标函数:选定下一个超参数后,通过实际评估目标函数来获得其性能。这涉及使用选定的超参数进行训练和验证,然后计算性能指标。
-
迭代:不断重复步骤5到7,直到达到预设的迭代次数或收敛条件为止。贝叶斯优化通过每次迭代逐步收敛到超参数的最佳值,从而在超参数空间中实现高效的搜索。
总的来说,Bayes-RF(基于贝叶斯优化的随机森林)是一种将贝叶斯优化应用于随机森林超参数调优的方法。通过不断地评估超参数组合的性能并更新代理模型,Bayes-RF能够高效地搜索超参数空间,并找到最佳的超参数组合,从而提高随机森林分类器的性能。

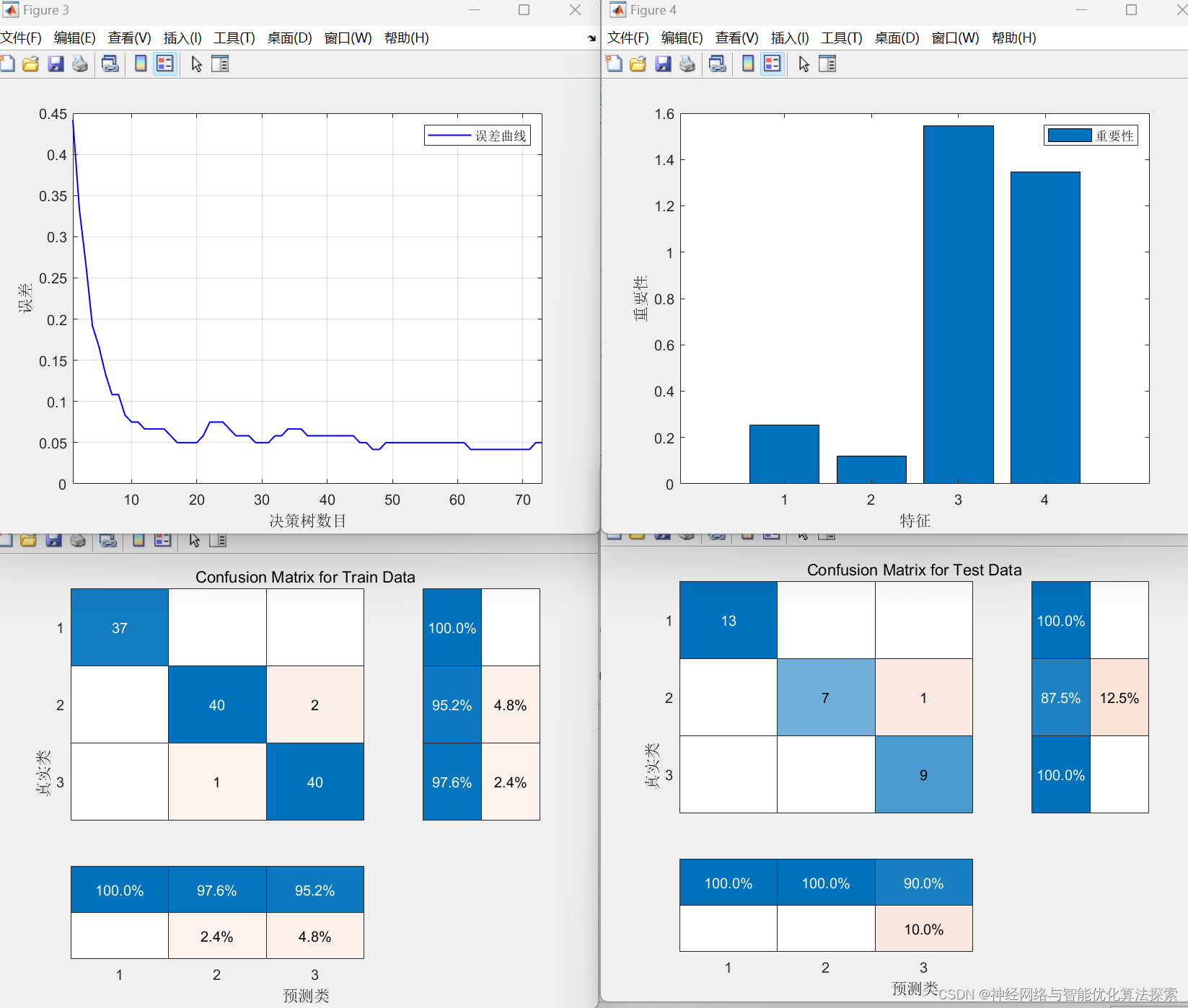
代码获取方式如下:
https://mbd.pub/o/bread/mbd-ZZ6Tm55y