1.数组和矩阵操作:
创建数组和矩阵:np.array, np.matrix
基本的数组操作:形状修改、大小调整、转置等
import numpy as np# 创建一个 2x3 的数组
A = np.array([[1, 2, 3], [4, 5, 6]])
print("数组 A:\n", A)# 将数组 A 转换为矩阵
B = np.matrix(A)
print("矩阵 B:\n", B)# 例一:
# 定义两个矩阵 C 和 D
C = np.array([[1, 2], [3, 4]])
D = np.array([[5, 6], [7, 8]])# 进行矩阵乘法
result = np.dot(C, D)
print("矩阵乘法结果:\n", result)# 例二:
x1 = np.array([[1, 2, 3], [4, 5, 6]])x2 = np.array([[1, 2], [3, 4],[5, 6]])# 矩阵乘法
print(x1.dot(x2))# 计算对角线之和
print(x2.trace())
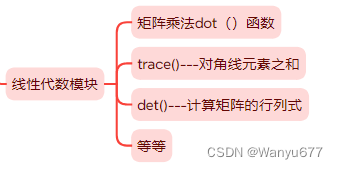
2.线性代数运算:
矩阵乘法:np.dot, np.matmul
内积和外积:np.inner, np.outer
点积:np.dot (对于一维数组)
对角线之和:np.trace()
# 定义系数矩阵和常数向量
coefficients = np.array([[3, 1], [1, 2]])
constants = np.array([9, 8])# 求解线性方程组
solution = np.linalg.solve(coefficients, constants)
print("线性方程组的解:\n", solution)3.特征值和特征向量:
计算矩阵的特征值和特征向量:np.linalg.eig
特征值分解:np.linalg.eigvalsh, np.linalg.eigh
# 定义一个需要计算特征值和特征向量的矩阵
E = np.array([[1, 2], [2, 1]])# 计算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(E)
print("特征值:\n", eigenvalues)
print("特征向量:\n", eigenvectors)4.矩阵分解:
奇异值分解(SVD):np.linalg.svd
卢分解(LU):np.linalg.lu
特征值分解(如前所述)
# 定义一个用于奇异值分解的矩阵
F = np.array([[2, 3], [4, 5]])# 进行奇异值分解
U, S, VT = np.linalg.svd(F)
print("U 矩阵:\n", U)
print("奇异值:\n", S)
print("VT 矩阵:\n", VT)5.线性方程组求解:
解决线性方程组:np.linalg.solve
计算矩阵的逆:np.linalg.inv
# 定义一个矩阵
G = np.array([[1, 2], [3, 4]])# 计算行列式
det_G = np.linalg.det(G)
print("矩阵 G 的行列式:\n", det_G)# 计算矩阵的迹
trace_G = np.trace(G)
print("矩阵 G 的迹:\n", trace_G)
6.行列式和迹:
计算矩阵的行列式:np.linalg.det
计算矩阵的迹:np.trace
# 创建一个 3x3 矩阵
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])# 计算矩阵的行列式
det_value = np.linalg.det(matrix)
print("矩阵的行列式为:", det_value)
# 使用之前定义的矩阵
trace_value = np.trace(matrix)
print("矩阵的迹为:", trace_value)7.范数和条件数:
计算向量的范数:np.linalg.norm
计算矩阵的条件数:np.linalg.cond
# 定义一个向量
vector = np.array([3, 4])# 计算向量的 L2 范数
norm = np.linalg.norm(vector)
print("向量的 L2 范数:\n", norm)8.三角函数和相关函数:
正弦、余弦等三角函数:np.sin, np.cos 等
反三角函数:np.arcsin, np.arccos 等
# 定义一个包含两个元素的数组,代表角度(以弧度为单位)
angles = np.array([0, np.pi / 2])# 计算正弦和余弦值
sine_values = np.sin(angles)
cosine_values = np.cos(angles)print("角度的正弦值:", sine_values)
print("角度的余弦值:", cosine_values)# 定义一个包含两个元素的数组,代表正弦和余弦值
sine_cosine_values = np.array([np.sin(np.pi / 4), np.cos(np.pi / 4)])# 计算反正弦和反余弦值
arc_sine_value = np.arcsin(sine_cosine_values[0])
arc_cosine_value = np.arccos(sine_cosine_values[1])print("反正弦值:", arc_sine_value)
print("反余弦值:", arc_cosine_value)