一、顺序统计量
定义:将长度为 n 的数组按升序排序后,第 i 个位置的数字是该数组的第 i 小的量,称之为第 i 顺序统计量。
则一个数组中的最小值是第1顺序统计量,最大值是第n顺序统计量,中位数是第 (n+1)/2 顺序统计量 (向下取整)
二、求最大值和最小值
最简单的方法就是将数组扫描一遍,找出其中的最大值与最小值,求出第1顺序统计量和第n顺序统计量。 时间复杂度即为
#include<stdio.h>
#include<string.h>
int maxn,minn=100001,n,a[10001];
int max(int a,int b)
{if(a<b) return b;else return a;
}
int min(int a,int b)
{if(a<b) return a;else return b;
}
int main()
{scanf("%d",&n);for(int i=1;i<=n;i++) scanf("%d",&a[i]);for(int i=1;i<=n;i++){maxn=max(maxn,a[i]);minn=min(minn,a[i]);}printf("%d %d",maxn,minn);return 0;
} 三、求第k顺序统计量
借助排序算法,直接通过已排序的数组 a [k] 即可完成,时间为排序算法的时间,快速排序,归并排序 ,冒泡排序,插入排序
,但是这些方法无疑浪费时间,排序进行了许多不必要的操作。
数组的划分
快速排序是通过数组的划分实现的,数组划分有多种方法。
1.第一种划分方法
// 以 a[left]为基准,将操作后的数组变为 a[left]所在位置的左边全部都小于 a[left]
// a[left]所在位置的右边全部都大于 a[left]
//即若k为a[left]的下标 a[left]为第k顺序统计量 if(left>=right) return;int temp=a[left];int i=left,j=right;while(i!=j){while(a[j]>=temp && i<j) j--;while(a[i]<=temp && i<j) i++;int t=a[i]; a[i]=a[j]; a[j]=t;}int t=a[left]; a[left]=a[i]; a[i]=t;算法实现过程: 这里可以了解到具体操作 (深入理解快速排序)

2.第二种划分方法
// 第二种划分方法,此时快速排序伪代码int partition(int a[],int left,int right)
{int x=a[right];int i=left-1;for(int j=left;j<=right-1;j++)if(a[j]<=x){i++;swap(a[i],a[j]);}swap(a[i+1],a[right]);return i+1;
}
void quick_sort(int a[],int l,int r)
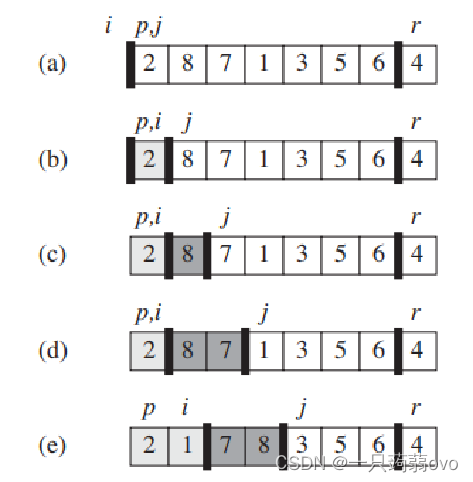
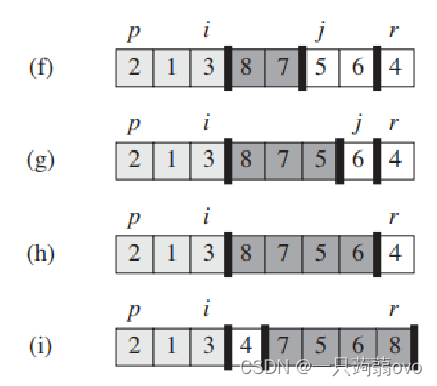
{if(l<r){int q=partition(a,l,r);quick_sort(a,l,q-1);quick_sort(a,q+1,r);}} 算法实现过程:以 a[]=[2,8,7,1,3,5,6,4]为例
法一 数组划分求出第k顺序统计量
1.先将数组中的某个元素(通常为数组末尾元素)按照上述方法划分左右两个区域(左边元素小于该元素,且右边元素大于该元素),并求出该元素的下标 a[ q ],此时该元素为 第 q 顺序统计量。
2.需要知道第k顺序统计量,则需要k与q进行比较,若 k<q 则只需要在左区域中找出第k小的数即可,同理若 k>q ,需要在右区域中找出第 k-q 小的数。
3.依次不断递归,直至划分出第k顺序统计量为止。
注意:每次数组划分元素后返回的q是数组下标,若某区域 [ l , r ] 中的元素通过划分返回的q,对应在区域中的顺序统计量为 q-l+1
int randselect(int a[],int l,int r,int k)
{int q=partition(a,l,r);int x=q-l+1; // 在[l,r]的第x位 [1,n]的第q位 if(x==k) return a[q];if(k<x) return randselect(a,l,q-1,k);else return randselect(a,q+1,r,k-x);
}法二 select算法----最坏情况为线性时间的选择算法
算法实现思路:

难点: select 函数 寻找中位数的中位数函数 find
关于select函数:
先找出中位数的中位数,再通过数组划分将数组以该数为基准划分。
关于find函数:
先将所有的数分为若干个小组,再在每个小组通过插入排序的方法,取出所有小组的中位数构成一个中位数数组(对于多出来的若干个元素同样取其中位数),再通过select选择算法,找出中位数数组的中位数(涉及两个函数的互相递归,较繁琐)
取中位数代码(注意区域左端L):
for(int i=1;i<num;i++) // 找出每组的中位数,并将其归为一个数组 mid[i]=ar[5*i-3+l];
if(h%5==0) mid[num]=ar[5*num-3+l];
else mid[num]=ar[5*(num-1)+l+(h%5-1)/2];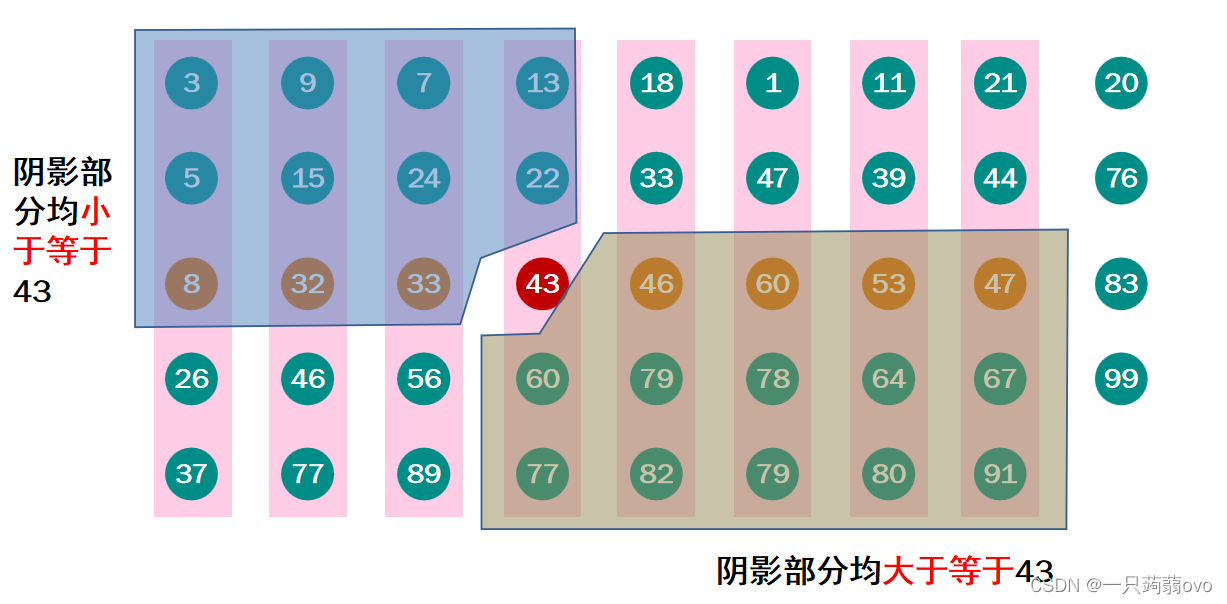
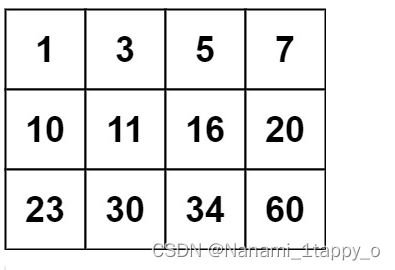
如图:找出中位数数组的中位数43,再进行partition将整个数组划分,再重复递归下去,直至找到需要找的那个第k顺序统计量 。
#include<stdio.h>
#include<iostream>
using namespace std;
#include<string.h>
int a[10001],n,num,k;
int mid[10001];
int find(int ar[],int l,int r);
void insertsort(int l,int r) // 插入排序
{for(int i=l;i<=r;i++){int x=a[i];int j=i-1;while(j>=l && a[j]>x){a[j+1]=a[j];j--;}a[j+1]=x;}
}
int partition(int ar[],int l,int r,int t) // 数组划分
{int i=l-1;int k;for(int j=l;j<=r;j++)if(ar[j]==t) k=j;swap(ar[k],ar[r]);for(int j=l;j<r;j++){if(ar[j]<=t){i++;swap(ar[j],ar[i]);}}swap(ar[i+1],ar[r]);return i+1;
}
int select(int ar[],int l,int r,int q)
{if(l>=r){return ar[l];}int t=find(ar,l,r); //返回的 t 代表的是 存储每一组中位数的临时数组的中位数int mi=partition(ar,l,r,t);int k=mi-l+1; //得到低区的元素个数if(q==k){ //表明已经找到该元素 return ar[mi];} else if(q<k){ //则要递归在 低区查找 return select(ar,l,mi-1,q);}else{ //递归在高区查找 return select(ar,mi+1,r,q-k); //在整个数组中的第i小元素在高区应该是 第 i-k 小元素了 }
}
int find(int ar[],int l,int r)
{int h=r-l+1;if(h%5==0) num=h/5;else num=h/5+1;int p1=l,p2=min(p1+4,r);for(int i=1;i<=num;i++) // 将每含5个元素的组进行插入排序 {insertsort(p1,p2);p1=min(p2+1,r);p2=min(p1+4,r);}for(int i=1;i<num;i++) // 找出每组的中位数,并将其归为一个数组 mid[i]=ar[5*i-3+l];if(h%5==0) mid[num]=ar[5*num-3+l];else mid[num]=ar[5*(num-1)+l+(h%5-1)/2];if(num==1) return mid[1];else return select(mid,1,num,(1+num)/2); //找出中位数的中位数
}
int main()
{scanf("%d",&n);scanf("%d",&k);for(int i=1;i<=n;i++) scanf("%d",&a[i]);printf("%d",select(a,1,n,k+1));return 0;
}