【数据结构】考研真题攻克与重点知识点剖析

前言

本文基础知识部分来自于b站：分享笔记的好人儿的思维导图与王道考研课程，感谢大佬的开源精神，习题来自老师划的重点以及考研真题。
此前我尝试了完全使用Python或是结合大语言模型对考研真题进行数据清洗与可视化分析，本人技术有限，最终数据清洗结果不够理想，相关CSDN文章便没有发出。

（考研真题待更新）

欢迎订阅专栏：408直通车

请注意，本文中的部分内容来自网络搜集和个人实践，如有任何错误，请随时向我们提出批评和指正。本文仅供学习和交流使用，不涉及任何商业目的。如果因本文内容引发版权或侵权问题，请通过私信告知我们，我们将立即予以删除。

文章目录

前言
第五章树与二叉树
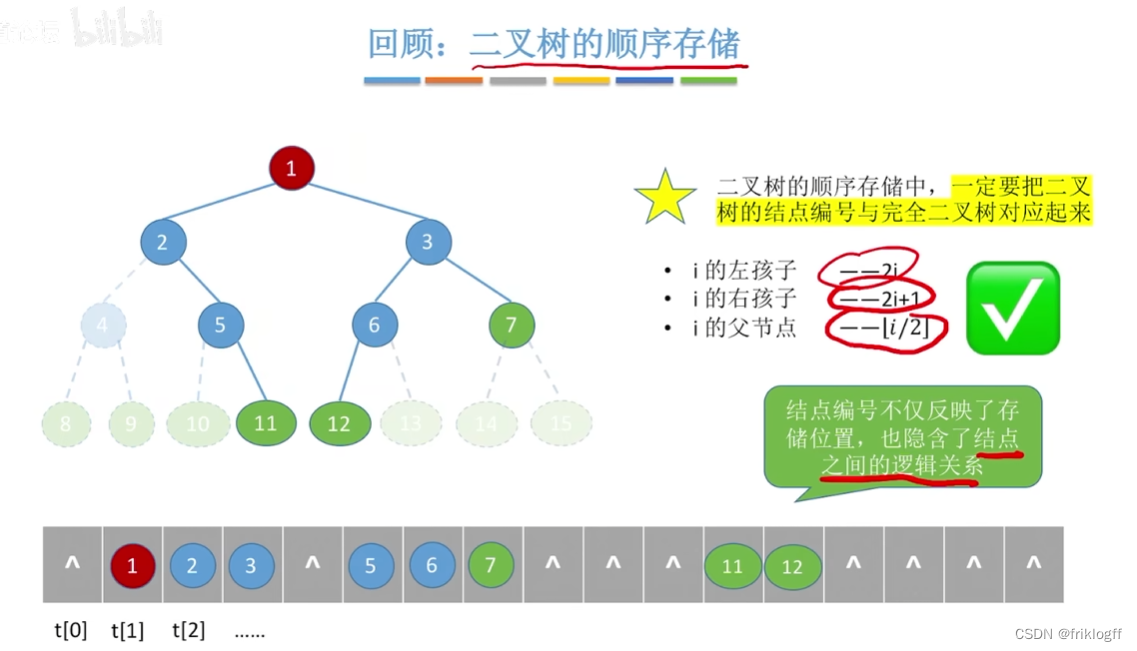
- 树的基本概念
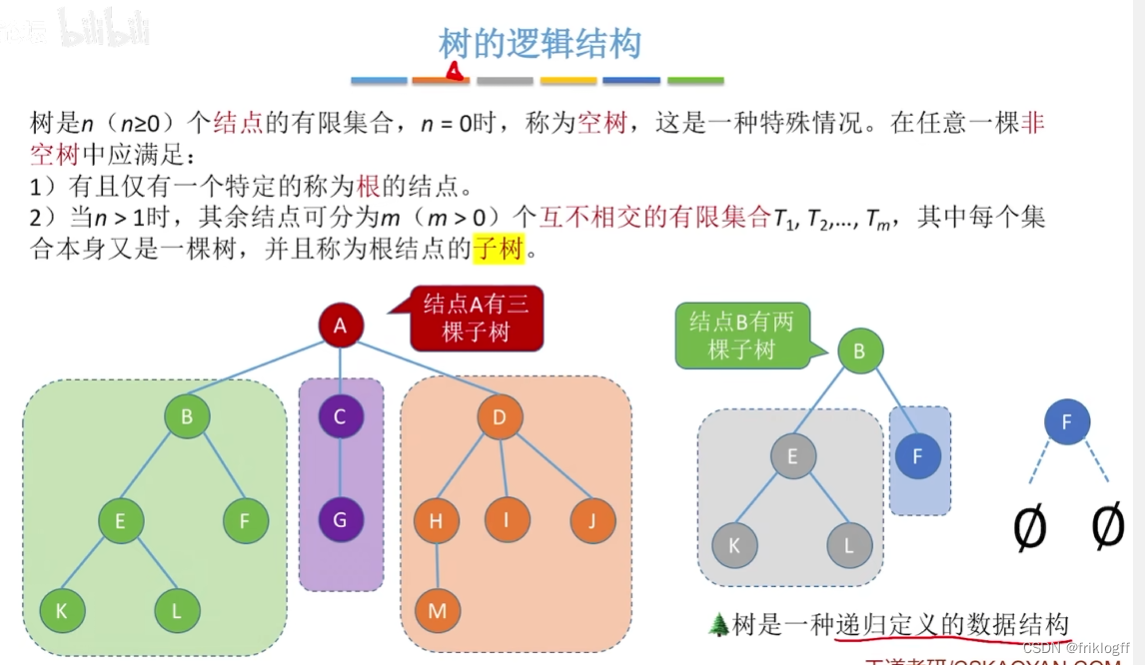
- - 树的定义（一种逻辑结构，具有层次关系）：树是n个结点的有限集
  - 树的基本术语
  - - 小结
  - 树的性质
  - - 小结
- 二叉树
- - 二叉树的定义
  - 特殊的二叉树
  - - 小结
  - 二叉树性质
  - 完全二叉树性质
  - - 小结
  - 存储结构
  - - 顺序存储结构
    - 链式存储结构
    - 小结
- 遍历二叉树和线索二叉树
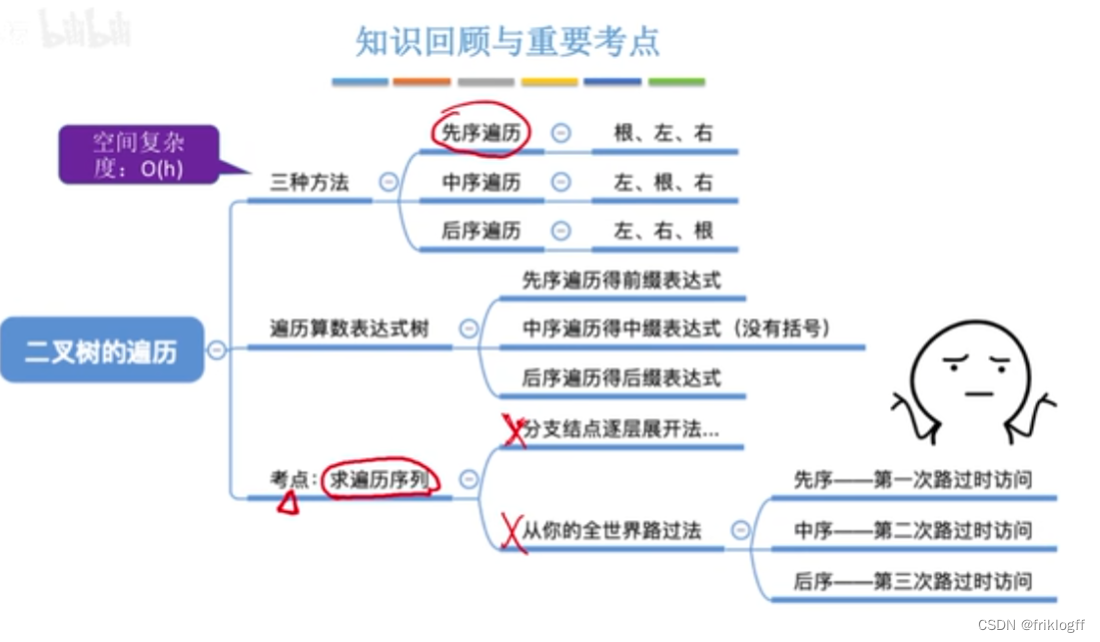
- - 二叉树的遍历
  - - 先序遍历
    - 中序遍历
    - 后序遍历
    - - 小结
    - 层次遍历
  - 由遍历序列构造二叉树
  - - 前序＋中序遍历序列
    - 后序＋中序遍历序列
    - 层序＋中序遍历序列
    - 小结
  - 线索二叉树
  - - 中序线索二叉树
    - - 代码实现
    - 先序线索二叉树
    - - 代码实现
    - 后序线索二叉树
    - - 代码实现
    - 小结
    - 线索二叉树找前驱/后继
    - - 中序线索二叉树找中序后继
      - 中序线索二叉树找中序前驱
      - 先序线索二叉树找中序后继
      - 先序线索二叉树找中序前驱
      - 后序线索二叉树找中序后继
      - 后序线索二叉树找中序前驱
    - 小结
- 树和森林
- - 树的逻辑结构
  - 树的存储结构
  - 树、森林与二叉树的转换
  - 树和森林的遍历
- 哈夫曼树及其应用
- - 基本概念
  - 哈夫曼树的定义
  - 哈夫曼树的构造
  - 哈夫曼编码
  - 多叉哈夫曼树（题目考点，类比外部排序的知识点），补0结点（虚叶结点）
- 并查集
- - 查
  - 并
  - 基本思路
  - 代码实现
  - 优化
  - - 小树合并到大树
    - 压缩路径
    - 小结
  - 并查集应用
  - 代码（巨无敌，就两行代码）
考研真题
- 408 - 2023

第五章树与二叉树

树的基本概念

树的定义（一种逻辑结构，具有层次关系）：树是n个结点的有限集

若n=0，称为空树
若n>0，则需要满足如下两个条件
- 有且仅有一个特定的称为根的结点
- 其余结点可分为m个互不相交的有限集T1、T2…Tm，其中每一个集合又是一棵树，并称为根的子树

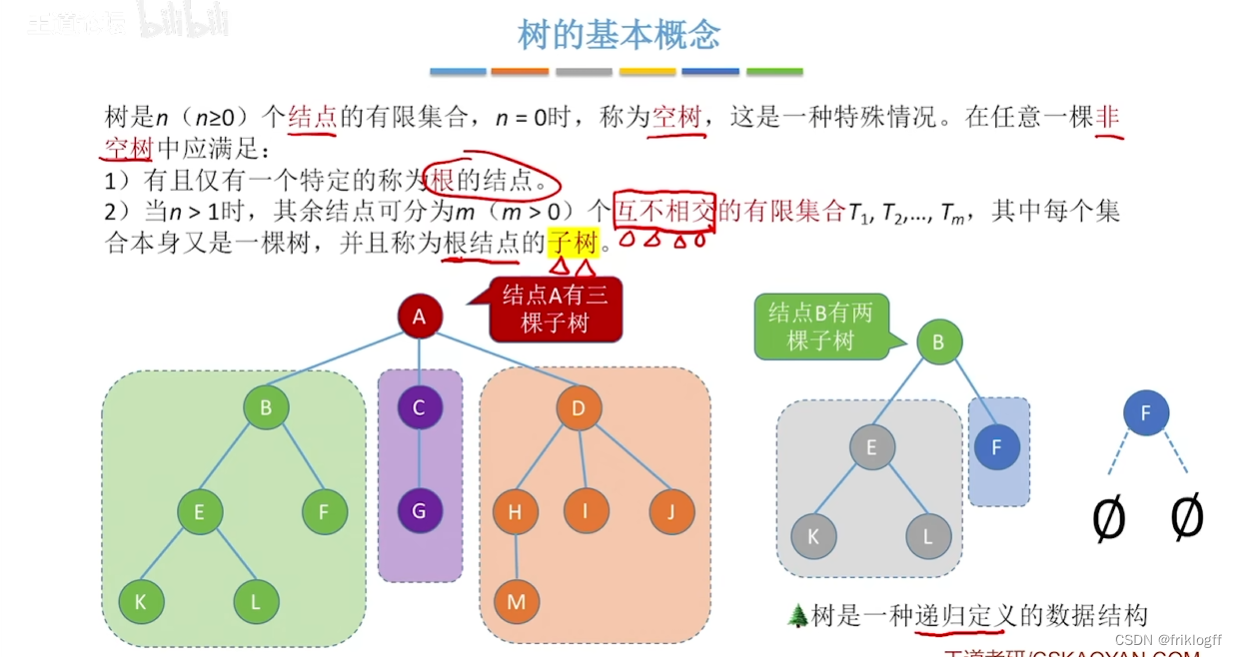
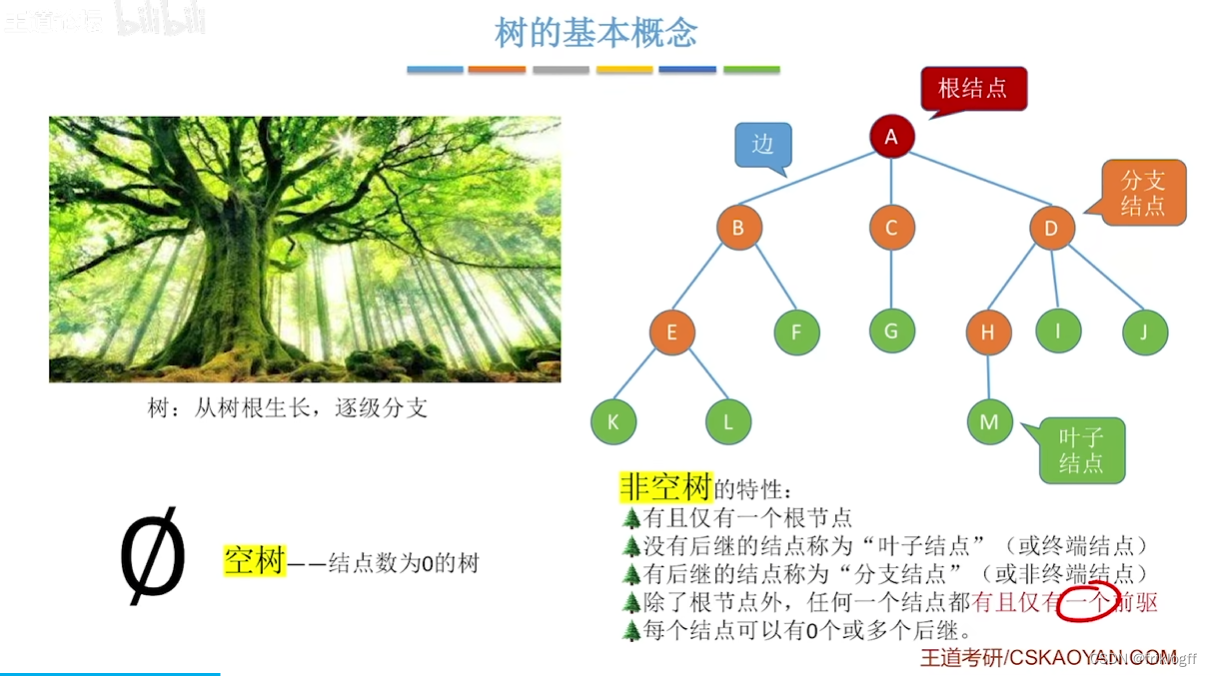
在这里插入图片描述

树的基本术语

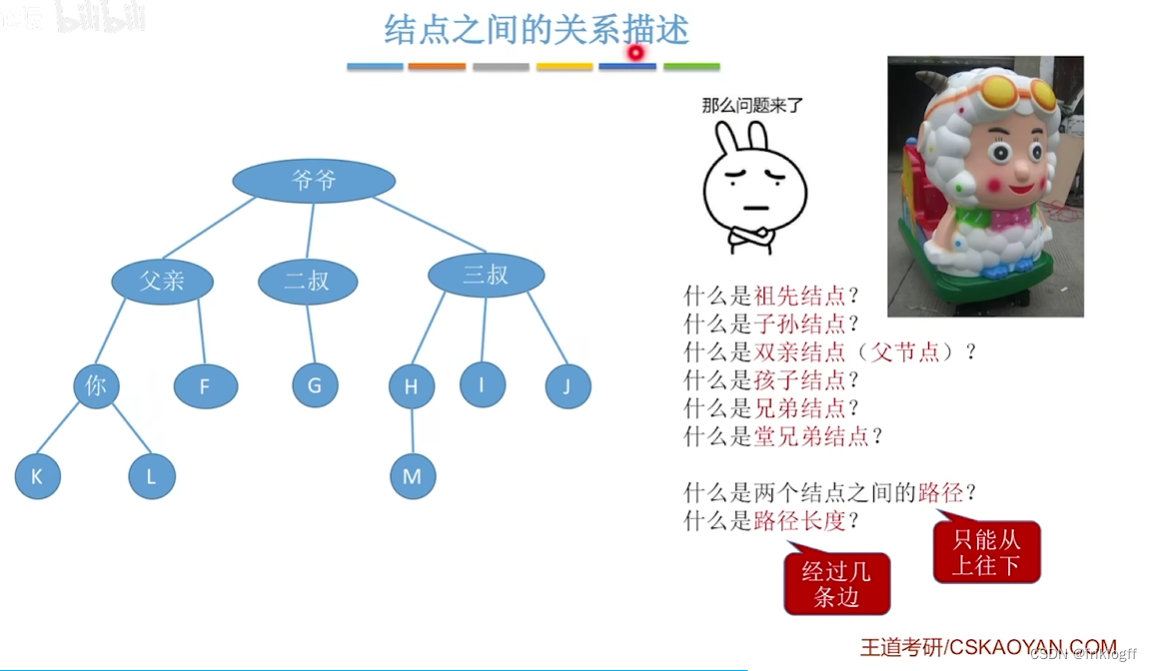
结点的关系
- 结点的祖先：从根到该结点所经分支上的所有结点
- 结点的子孙：以某结点为根的子树中的任一结点
- 双亲和孩子：结点的子树的根称为该结点的孩子，该结点称为孩子的双亲
- 兄弟：有相同双亲的结点
- 堂兄弟：双亲在同一层
结点的度
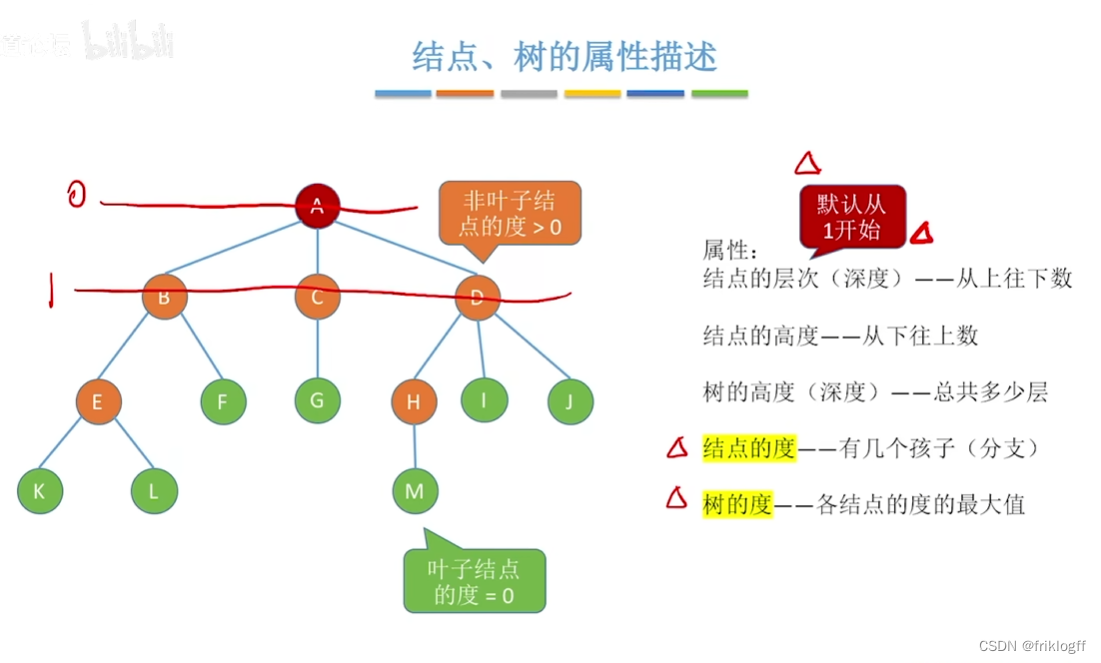
- 树中一个结点的孩子个数，树中结点的最大度数称为树的度
分支结点（非终端结点）
- 度大于0的结点
叶子结点（终端结点）
- 度为0的结点
结点的层次
- 从树根开始定义，根结点为第一层
结点的深度
- 从根结点开始自顶向下逐层累加
结点的高度
- 从叶结点开始自底向上逐层累加
树的高度（深度）
- 树中结点的最大层数
有序树和无序树
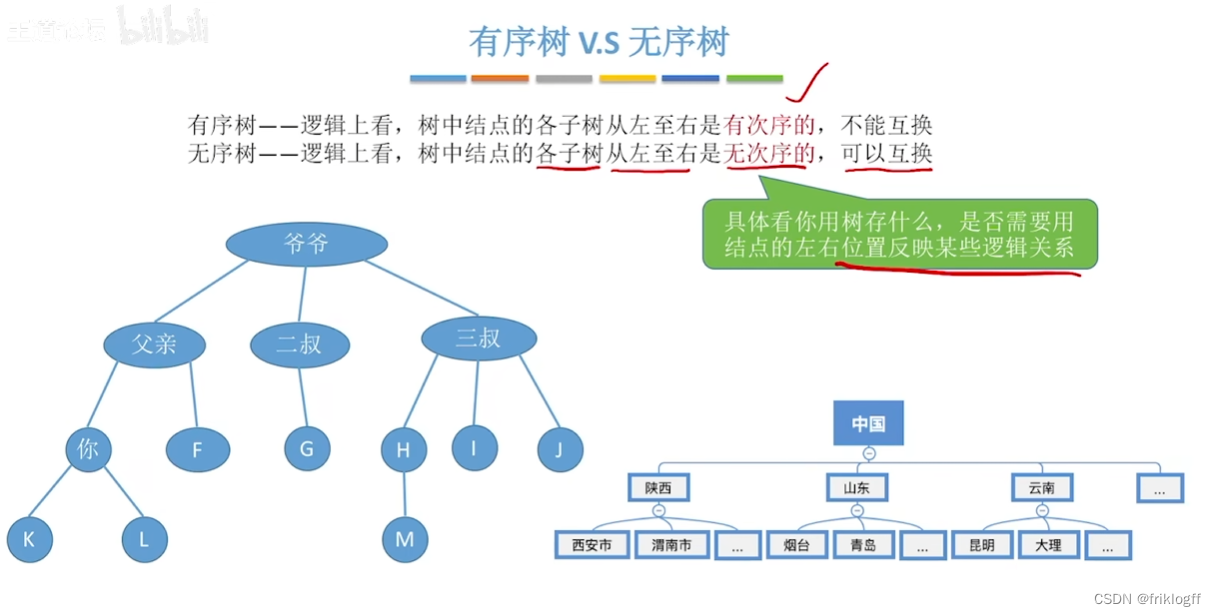
- 树中结点的各子树从左到右时有次序的，则该树为有序树，反之无序树
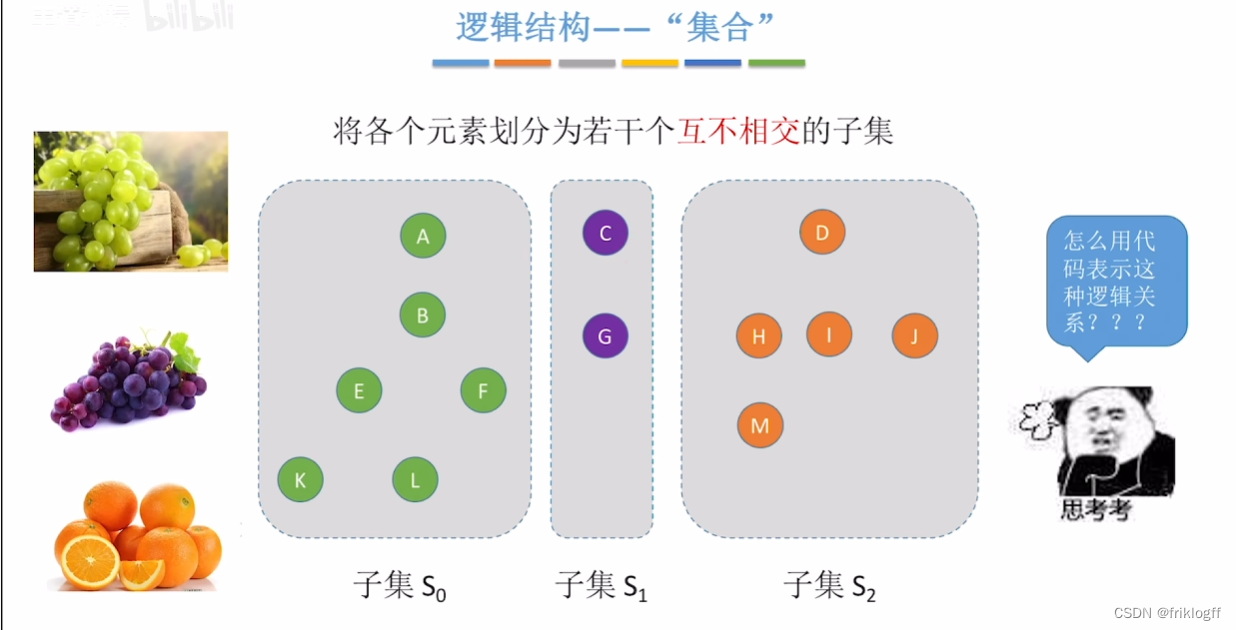
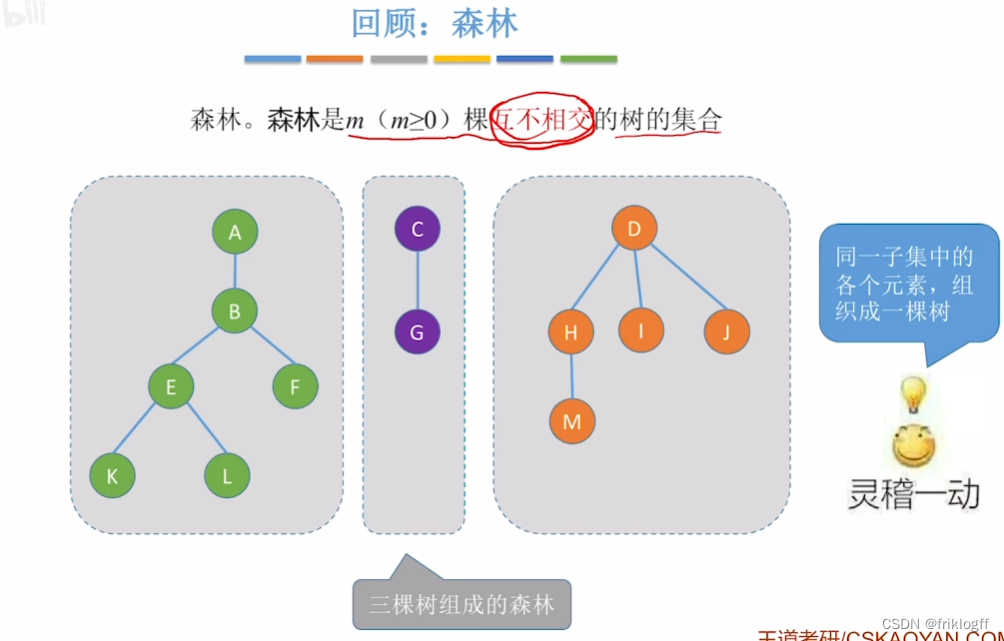
森林
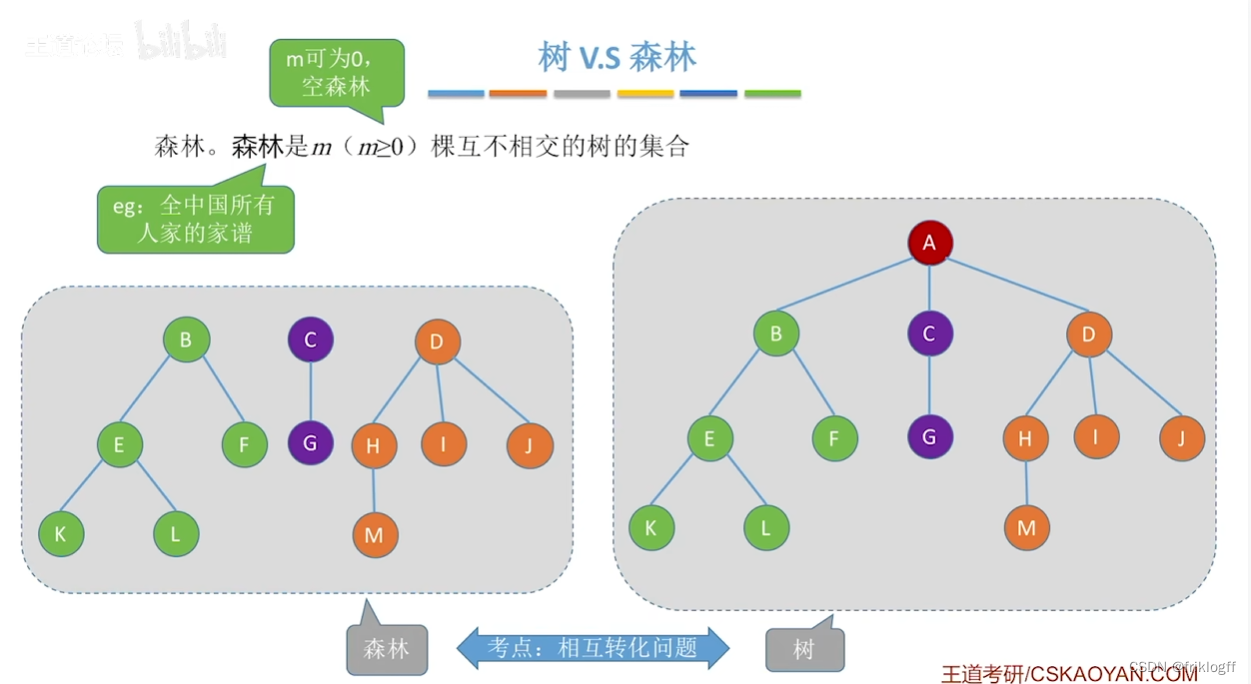
- n课互不相交的树的集合

小结

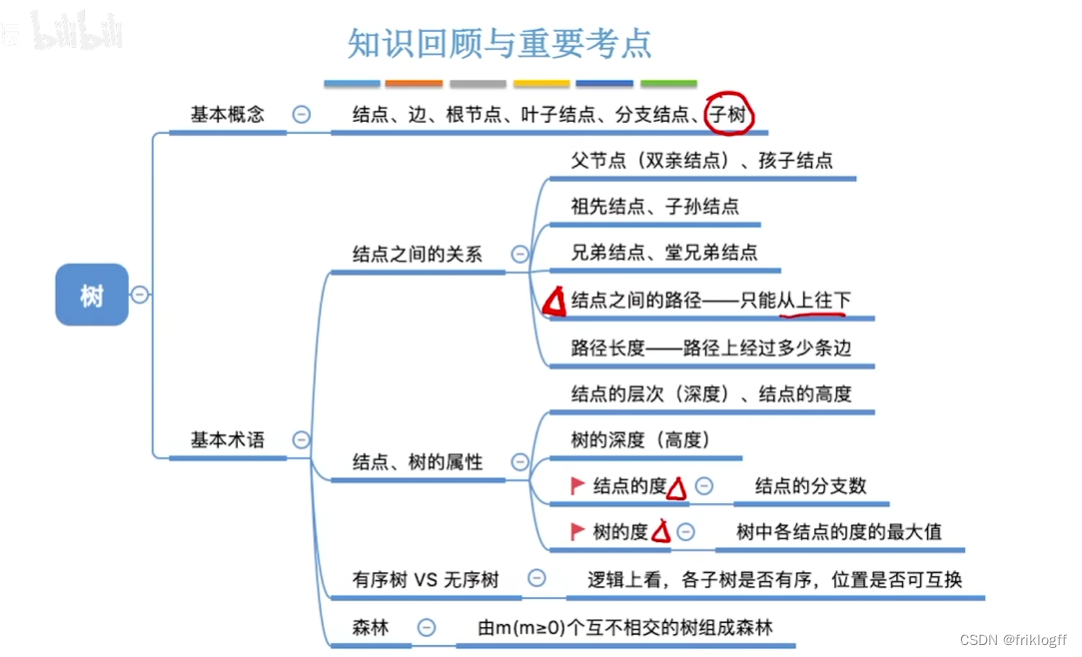
在这里插入图片描述

树的性质

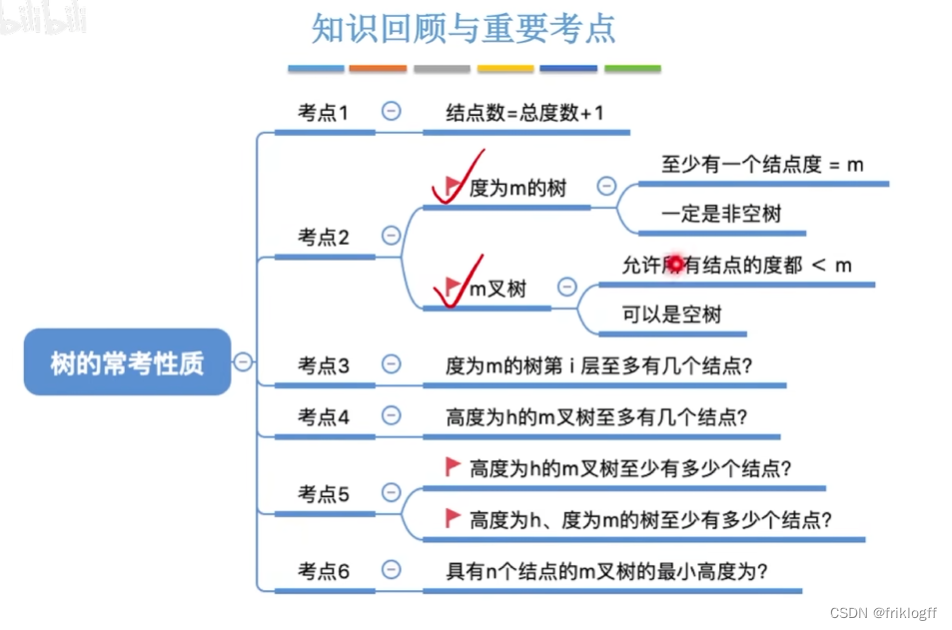
树的结点数=总度数+1
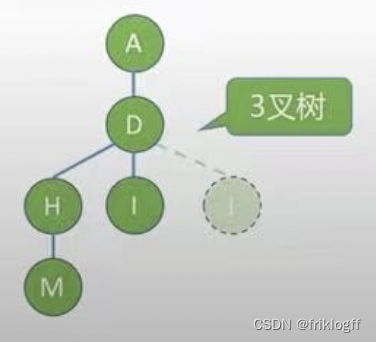
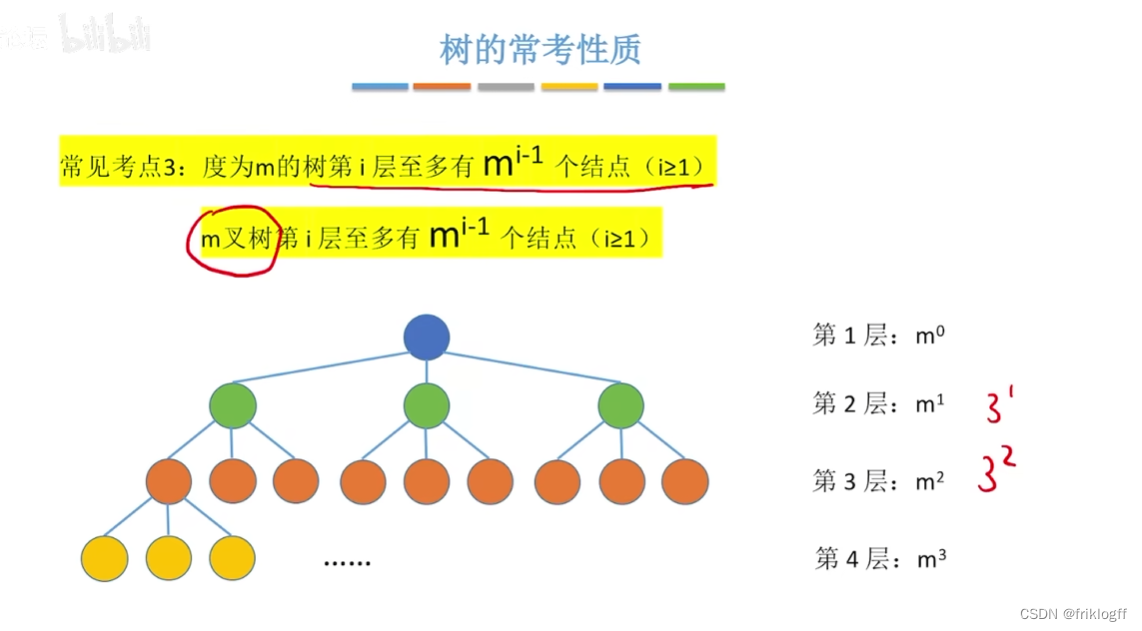
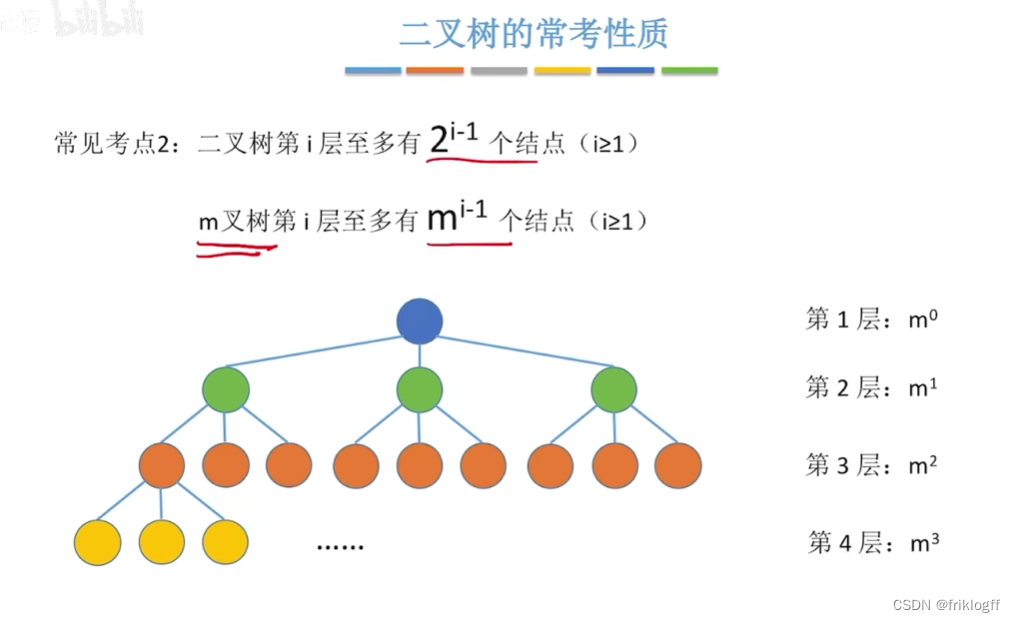
m叉树
- - 每个结点最多只能有m个孩子的树（可以是空树）
    - 允许所有结点度<m
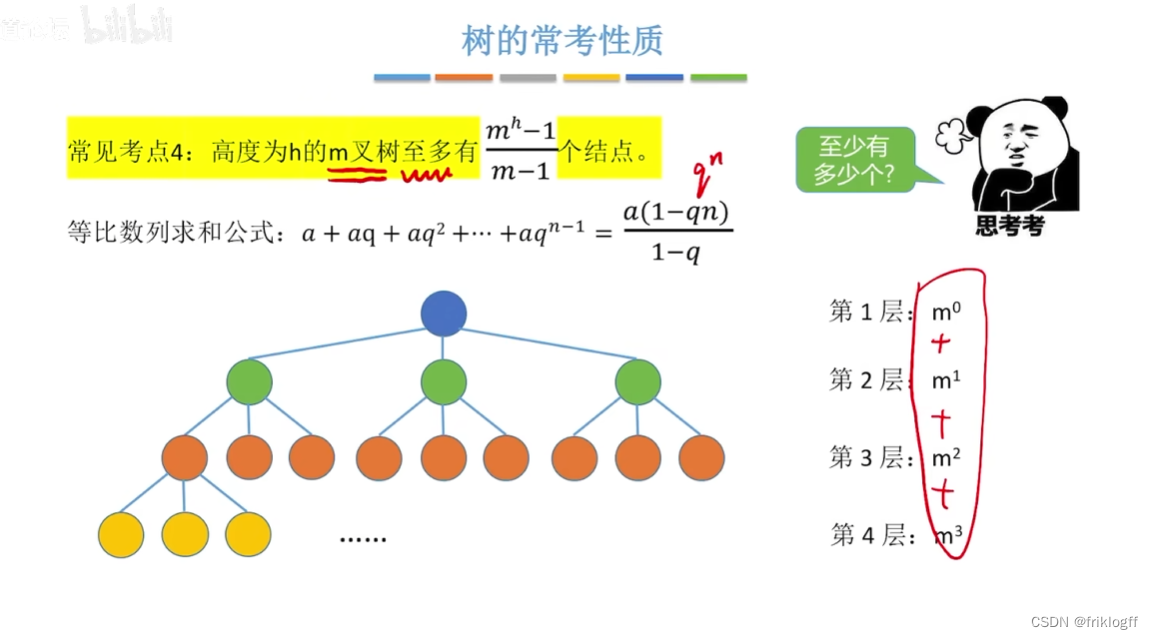
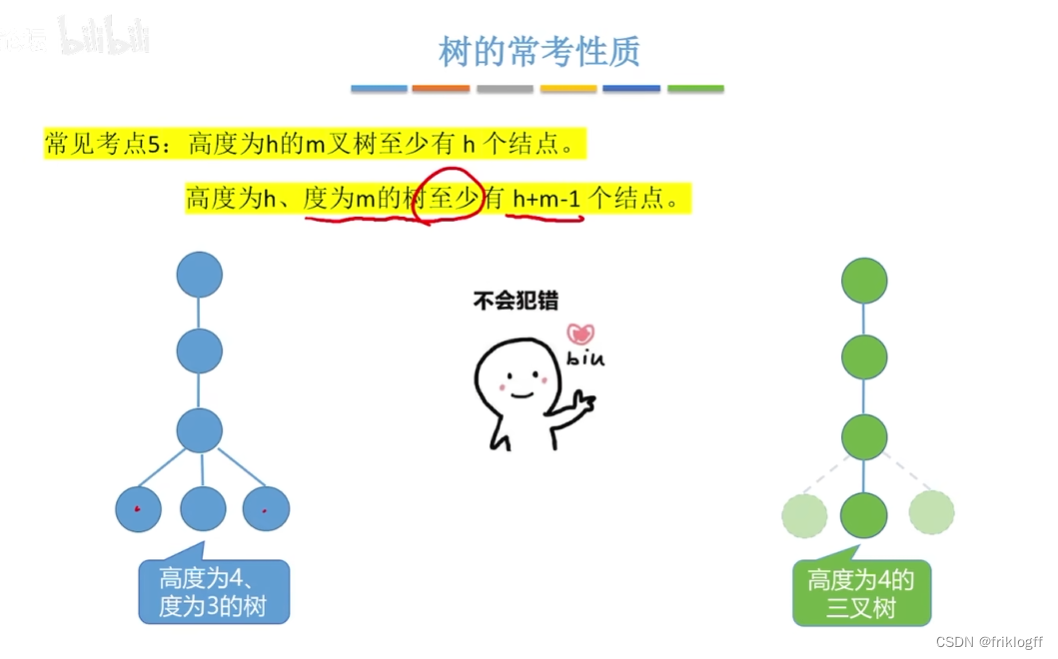
  - 高度为h的m叉树至少有h个结点，至多有(m^h-1)/(m-1)个结点（等比数列）
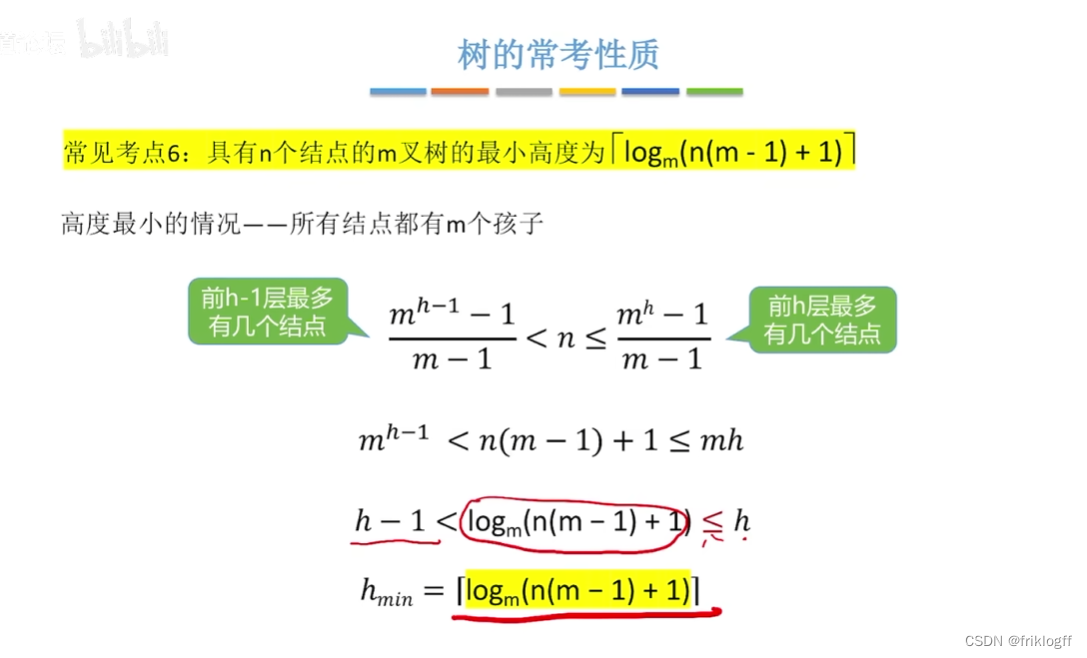
  - 具有n个结点的m叉树最小高度为 ⌈logm (n(m-1)+1)⌉
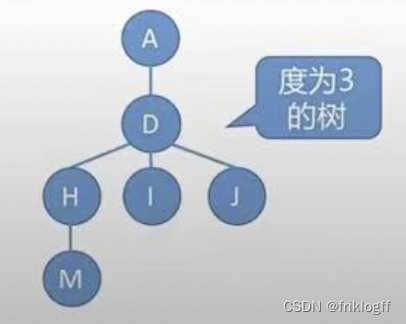
度为m的树
- - 任意结点的度<=m
  - 至少有一个结点度=m
  - 一定是非空树，至少有m+1个结点

在这里插入图片描述

小结

在这里插入图片描述

二叉树

二叉树的定义

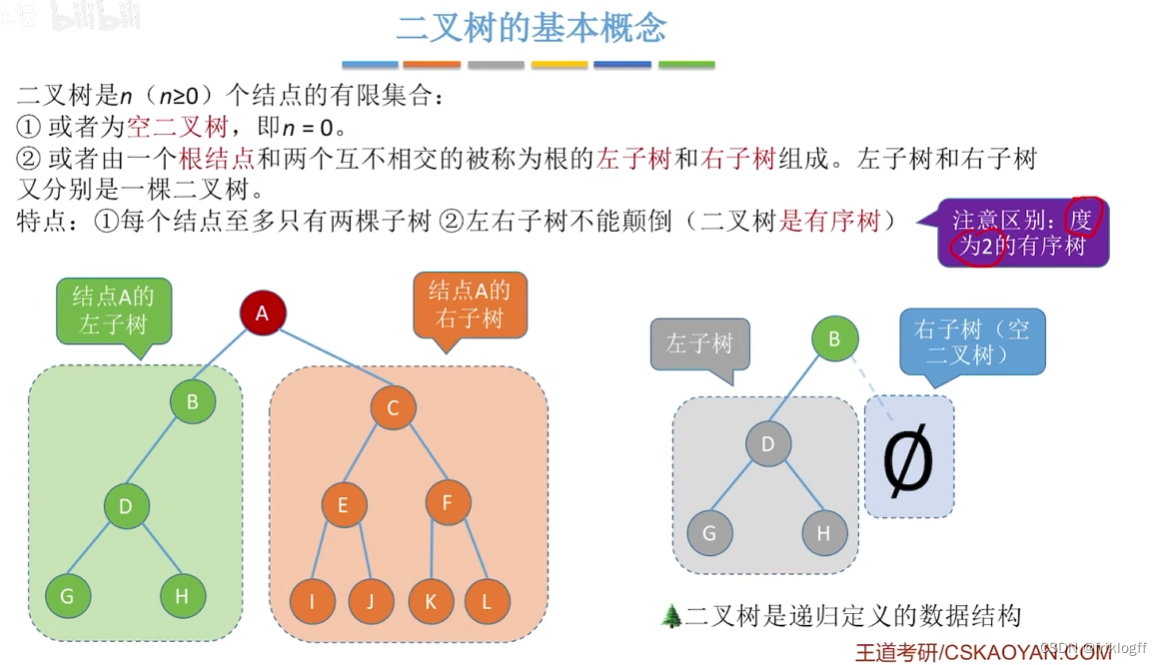
在这里插入图片描述

二叉树是n个结点的有限集，它或者是空集（n=0），或者由一个跟结点及两棵互不相交的分别称作这个根的左子树和右子树的二叉树组成
特点
- 二叉树是有序树，子树有左右之分，其次序不能颠倒
- 二叉树可以是空集合，根可以有空的左子树或空的右子树
二叉树的性质
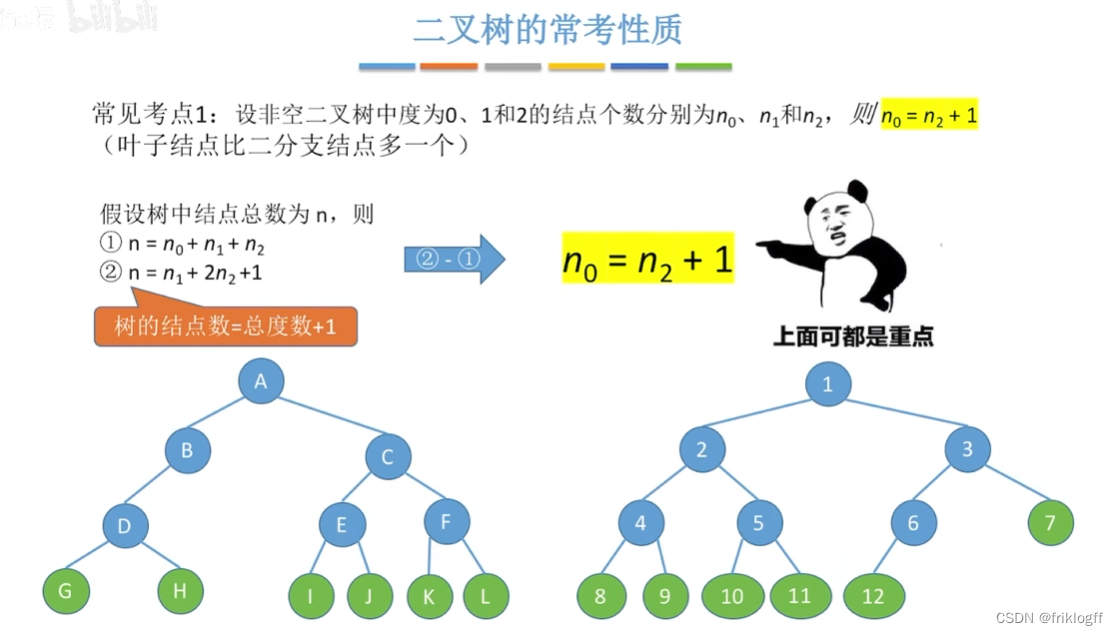
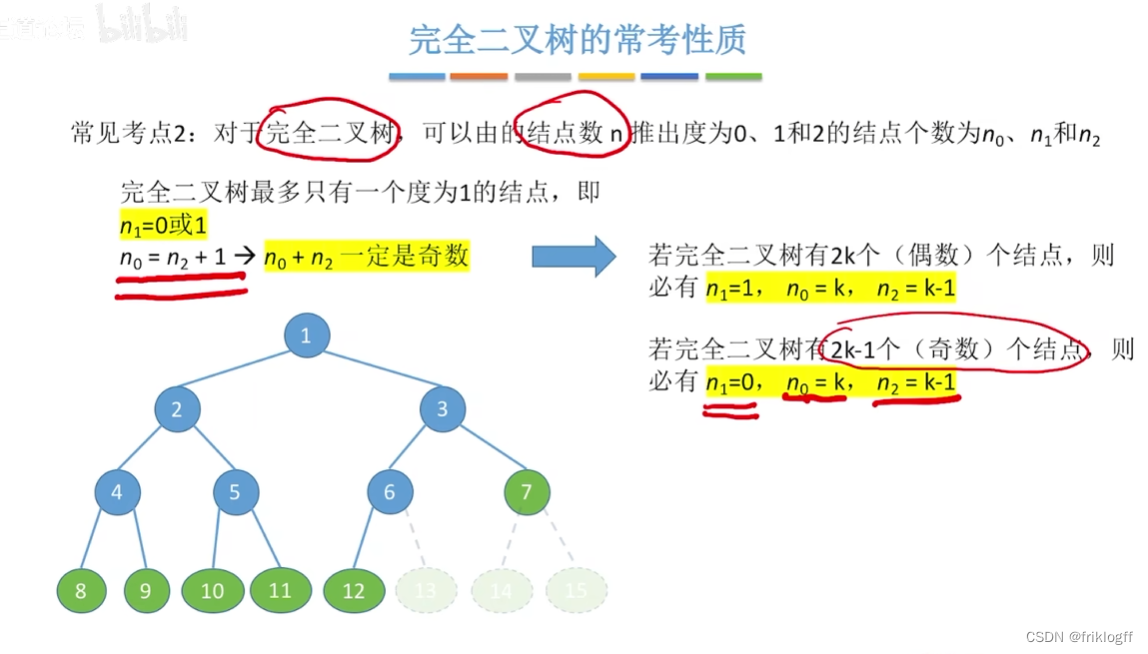
- 非空二叉树上的叶子结点数等于度为2的结点数+1
- 非空二叉树上第k层上至多有2^k-1个结点
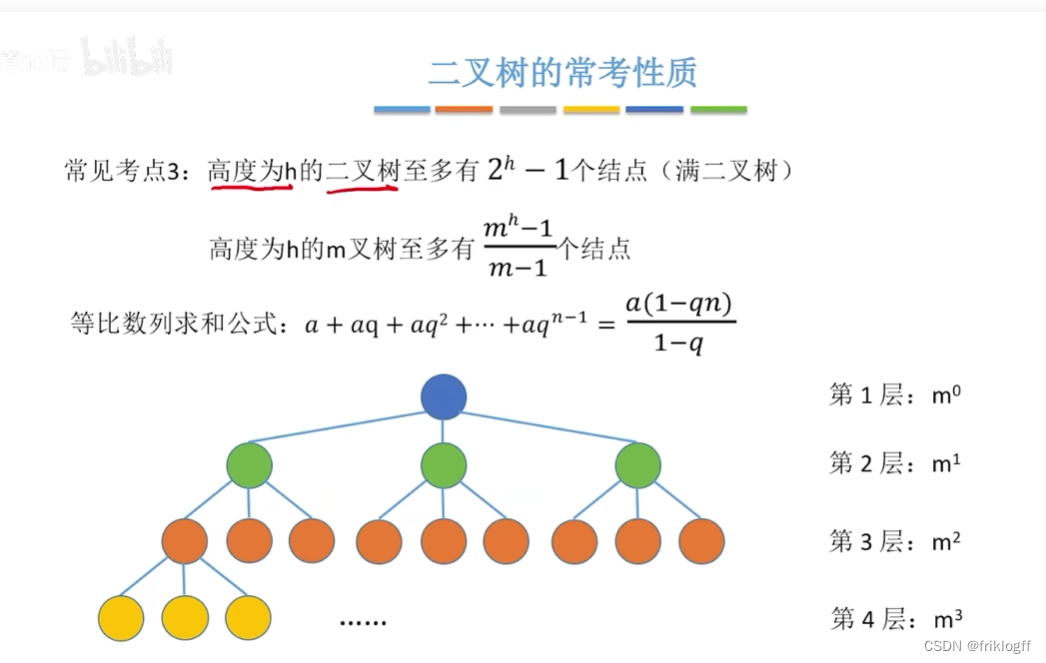
- 高度为h的二叉树至多有2^h-1结点

特殊的二叉树

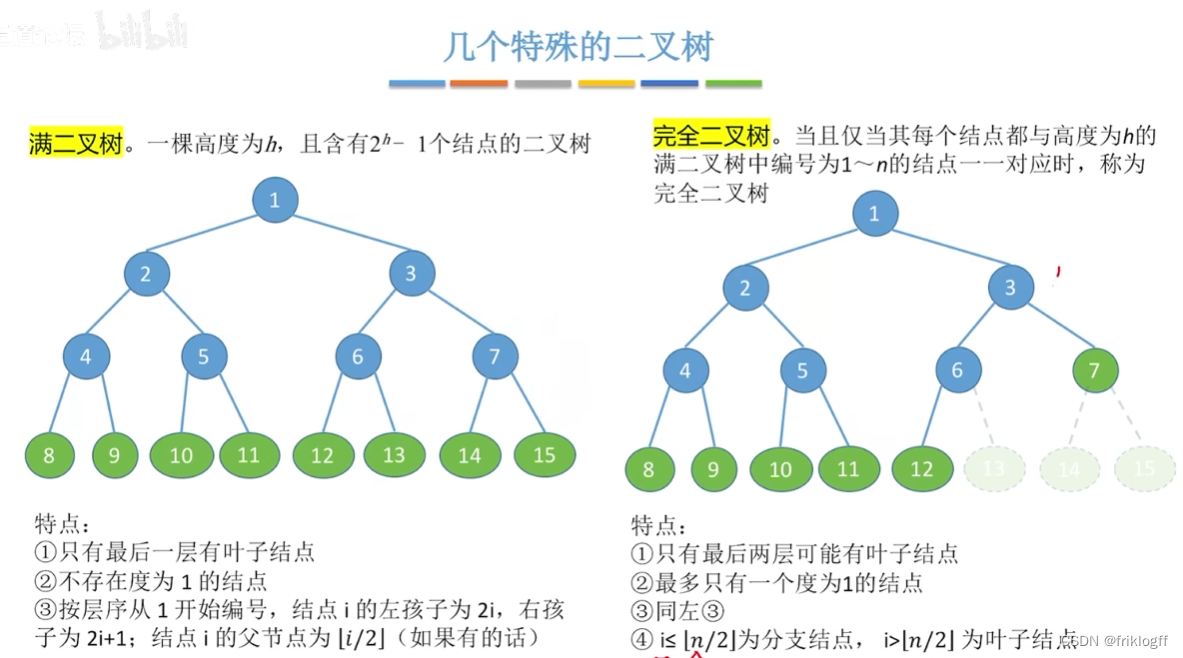
在这里插入图片描述

满二叉树
- 概念
  - 一颗高度为h，且含有2^h-1个结点的二叉树称为满二叉树
- 性质
  - 对于编号为i的结点
    - 双亲为⌊i/2⌋
    - 若有左孩子，则左孩子为2i
    - 若有右孩子，则右孩子为2i+1
完全二叉树
- 概念
  - 高度为h，有n个结点的二叉树，当且仅当其每个结点都与高度为h的满二叉树中编号为1-n的结点一一对应
- 特点
  - i<=⌊n/2⌋则结点为分支结点，否则为叶子结点
  - 按编号，一旦出现某结点为叶子结点或只有左孩子，则编号大于i的结点均为叶子结点
- 性质
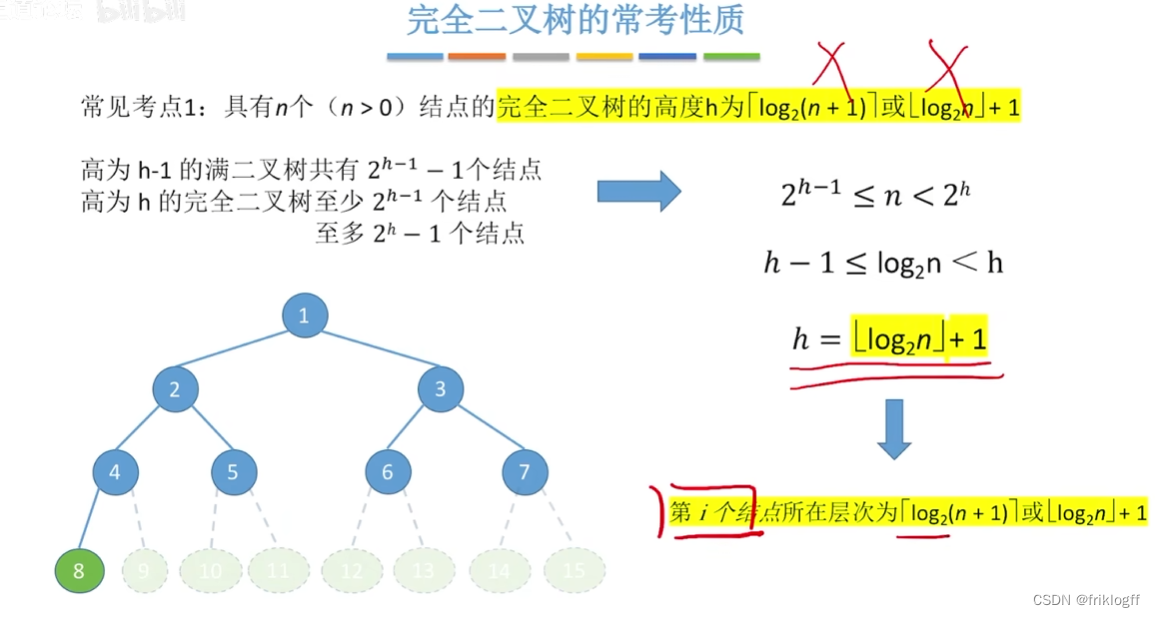
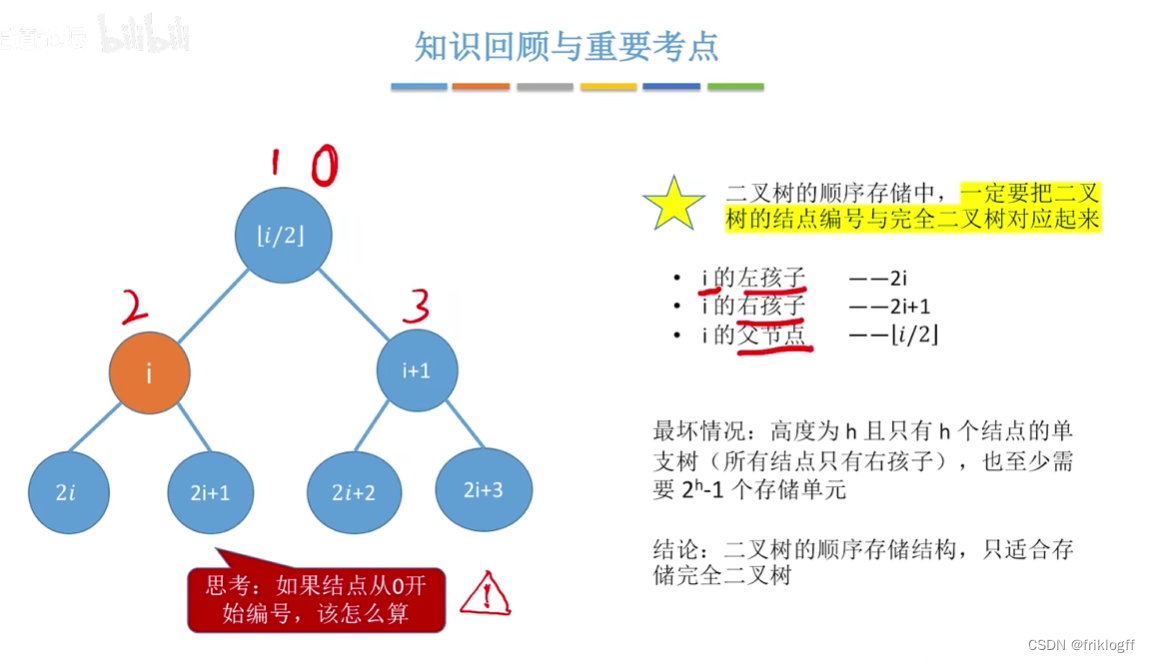
  - 具有n个结点的完全二叉树的深度为⌊log2n⌋+1
    - 证明：二叉树深度为k，结点数量：2^(k-1)<=n<2k，不等式取对数，推出
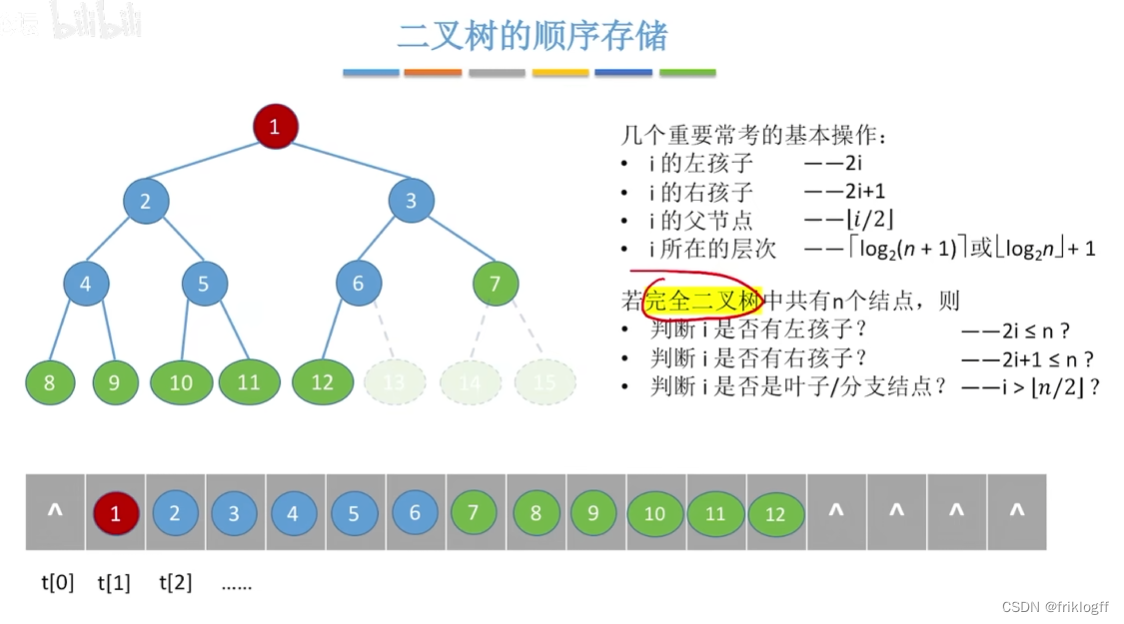
  - 完全二叉树依次编号1,2,…,n，则对任一结点i有
    - 如果i>1，则其双亲结点是⌊i/2⌋
    - 如果2i>n，则结点i为叶子结点，无左孩子
    - 如果2i+1>n，则结点i无右孩子
    - 结点i所在层次（深度）为⌊log2i⌋+1

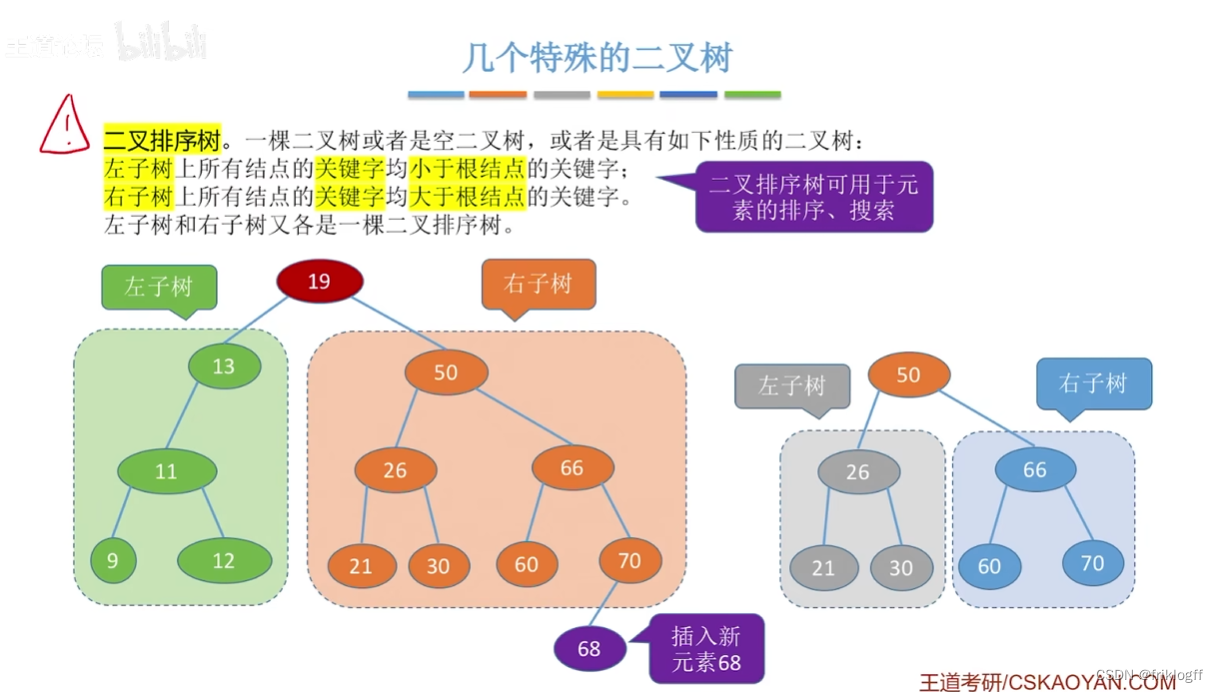
在这里插入图片描述

二叉排序树
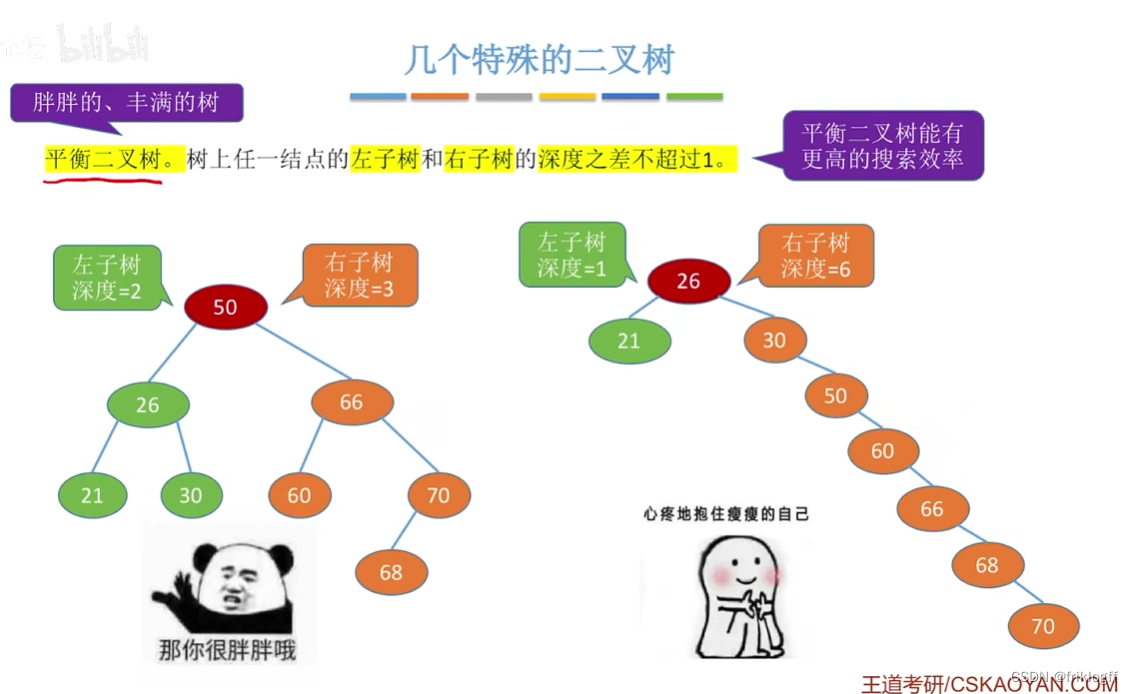
平衡二叉树

小结

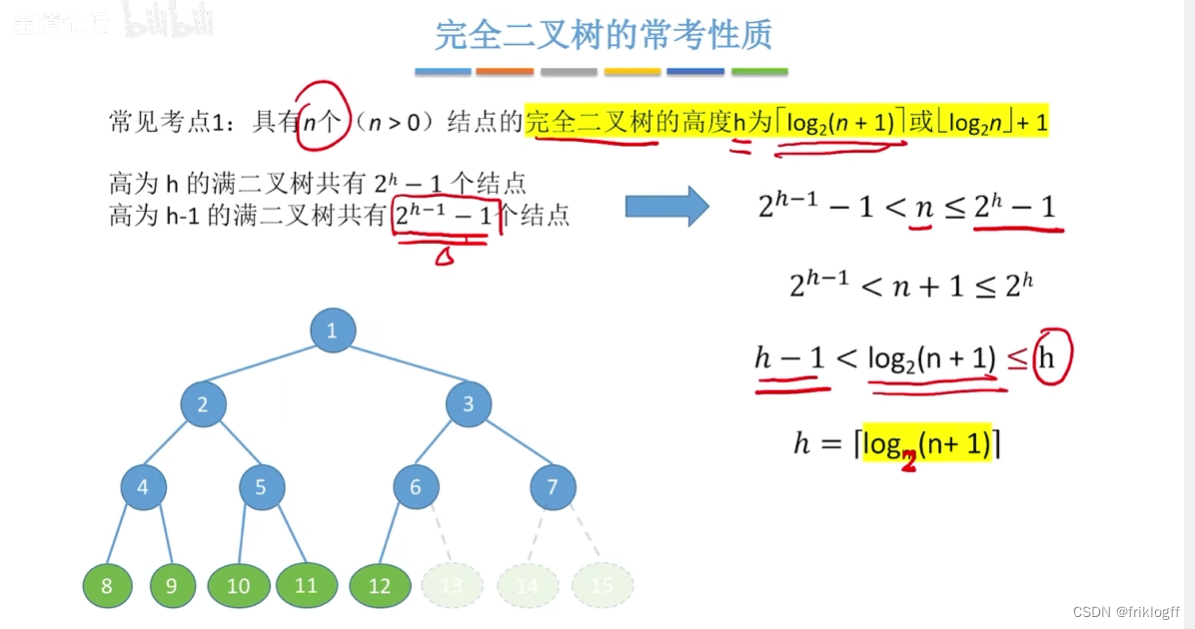
在这里插入图片描述

二叉树性质

在这里插入图片描述

完全二叉树性质

在这里插入图片描述

小结

在这里插入图片描述

存储结构

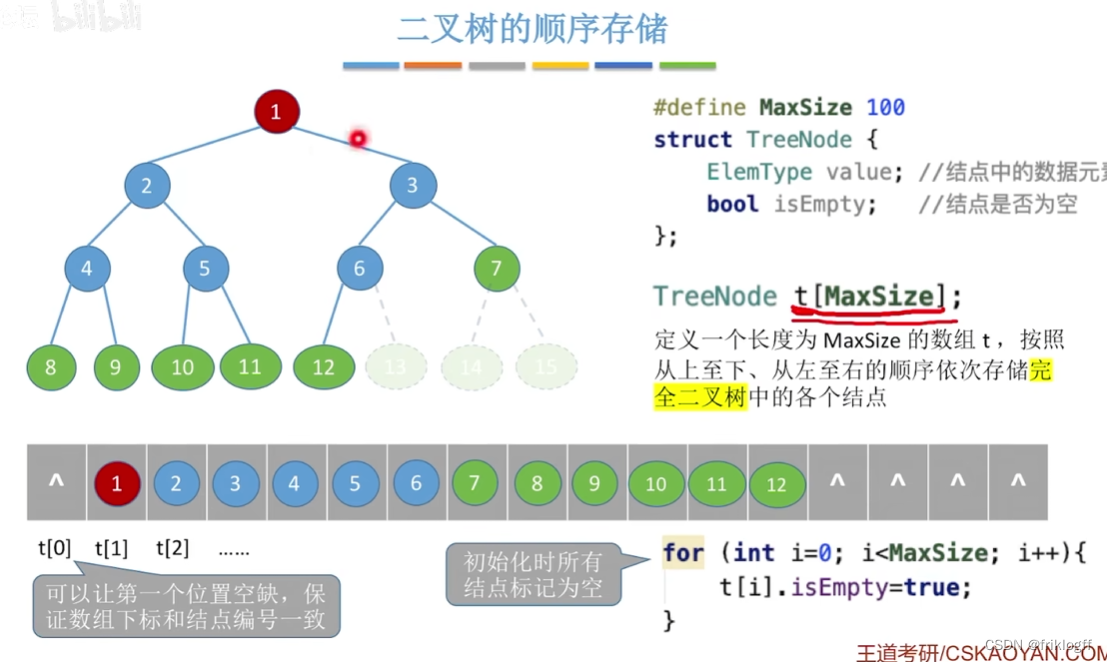
顺序存储结构

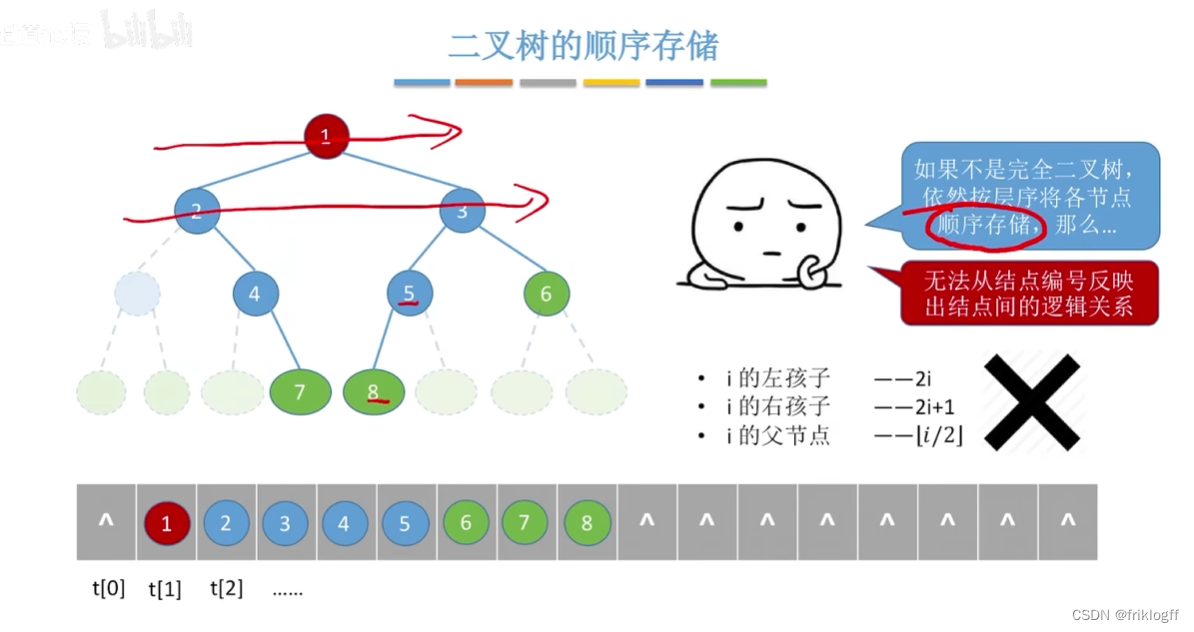
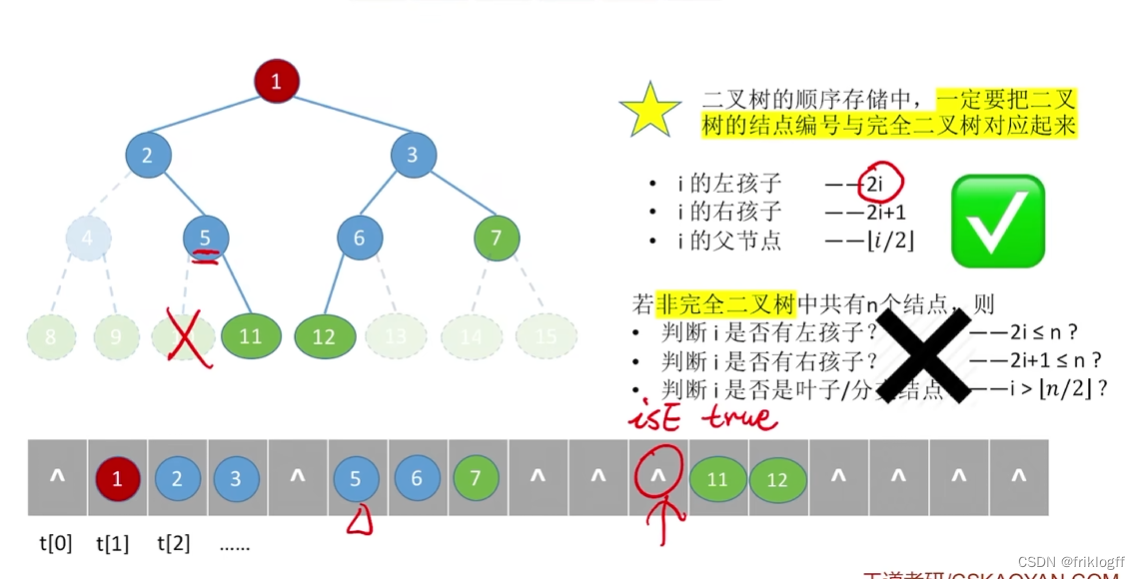
在这里插入图片描述

用一组地址连续的存储单元存储二叉树，为了反映二叉树结点间的逻辑关系，需要添加很多不存在的空结点
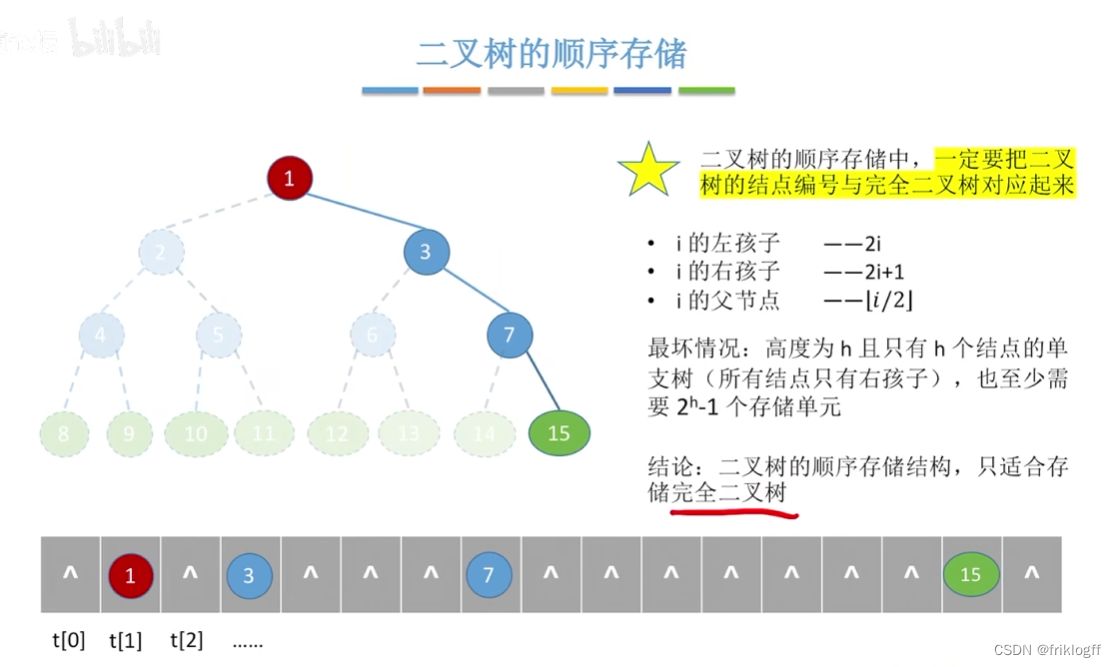
浪费空间，存储右单支树时，深度为k需要2^k-1的空间

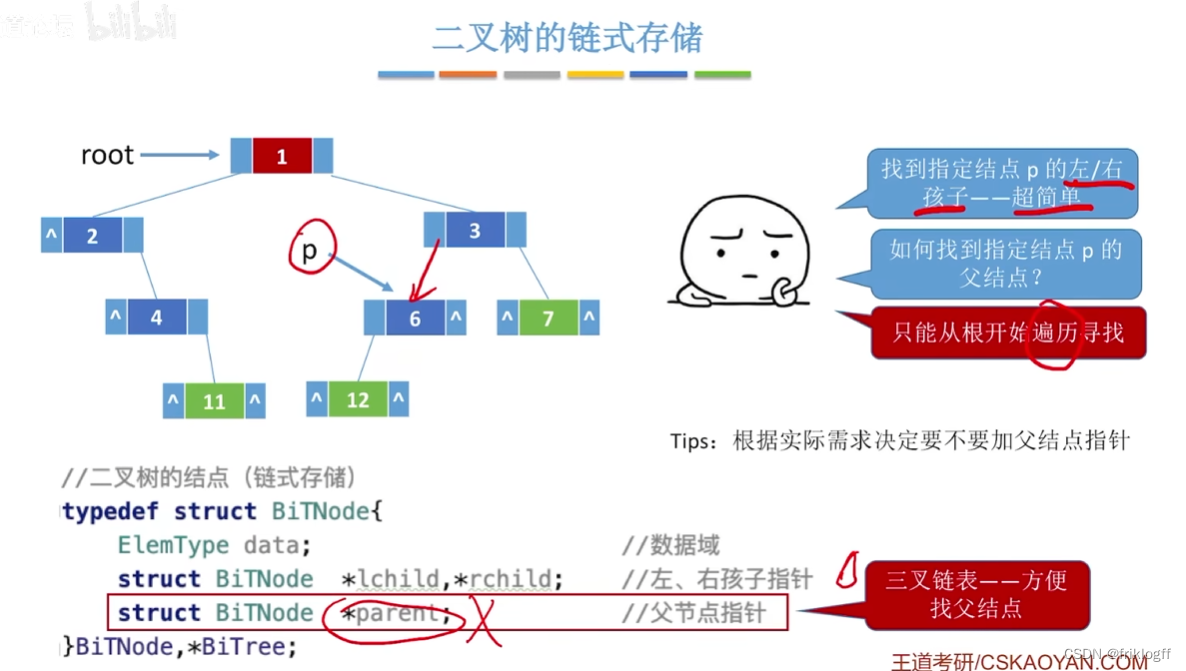
在这里插入图片描述

链式存储结构

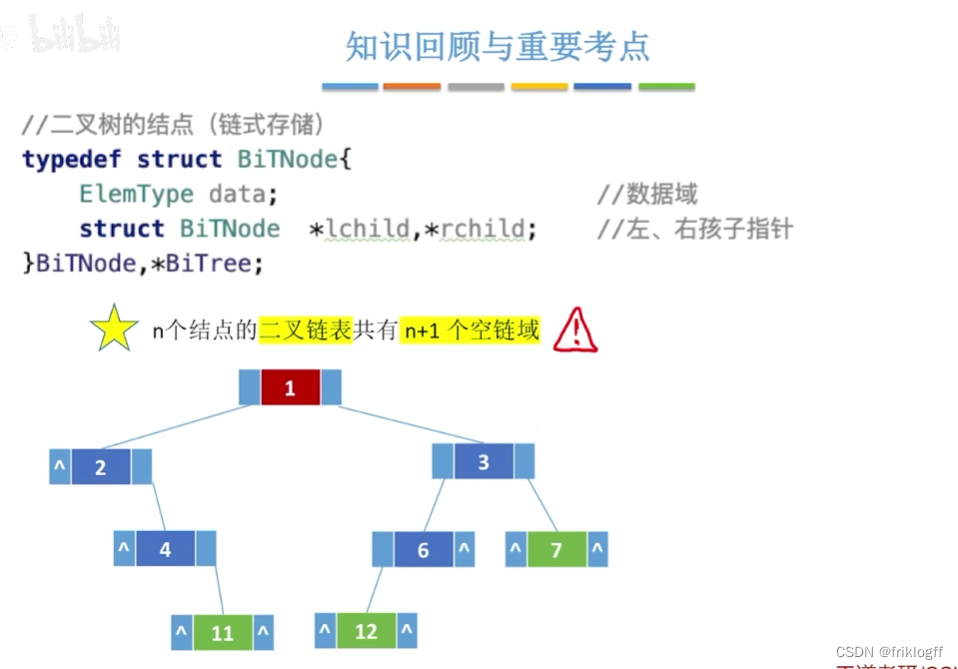
二叉链表
- 含有n个结点的二叉链表中，含有n+1个空链域
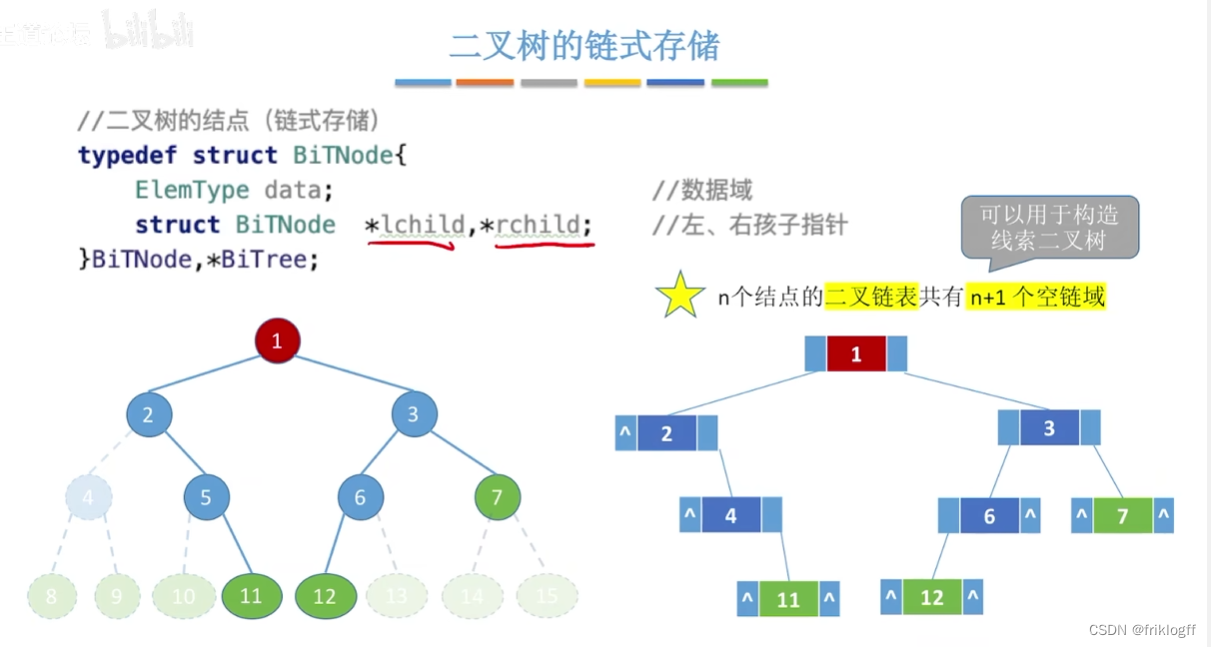
- 有n-1个结点头上连一个指针
  2n-(n-1)=n+1

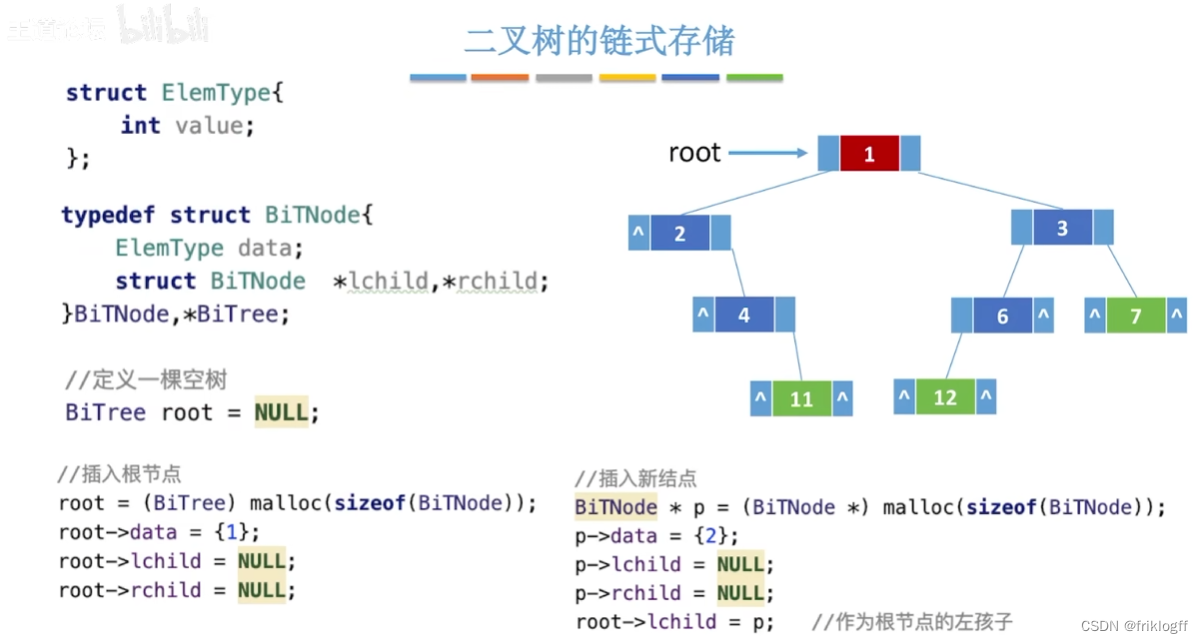
在这里插入图片描述

三叉链表（带父结点）

小结

在这里插入图片描述

遍历二叉树和线索二叉树

二叉树的遍历

概念
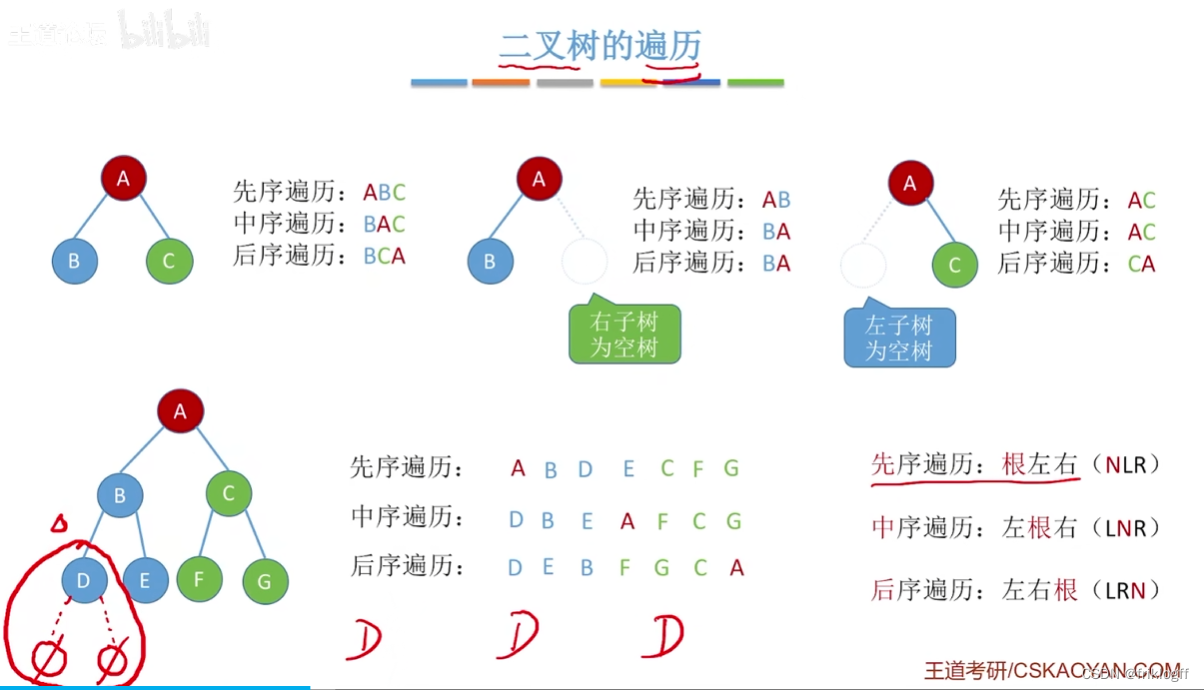
二叉树的遍历是指按某条搜索路径访问树中每个结点，每个结点均被且仅被访问一次

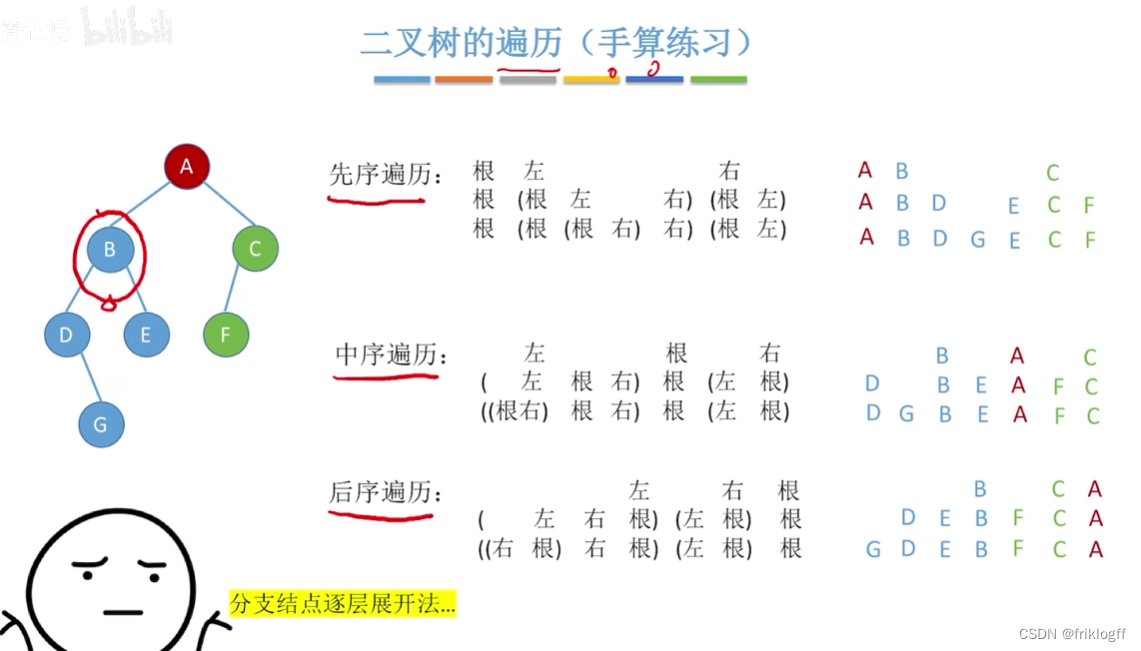
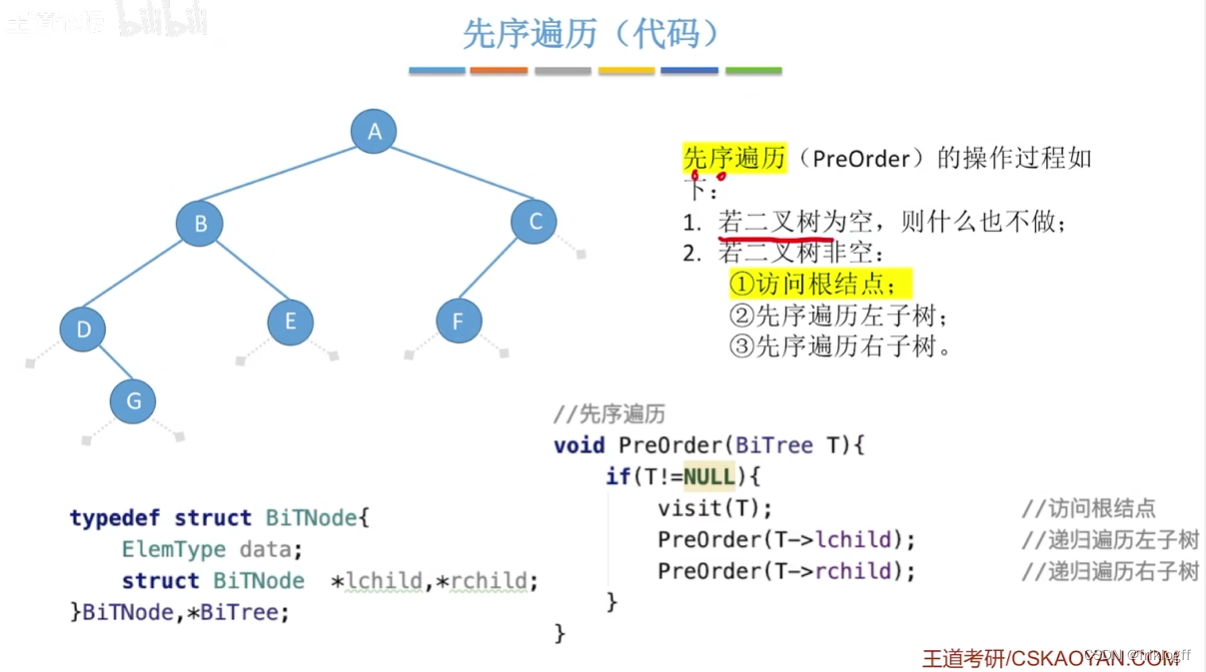
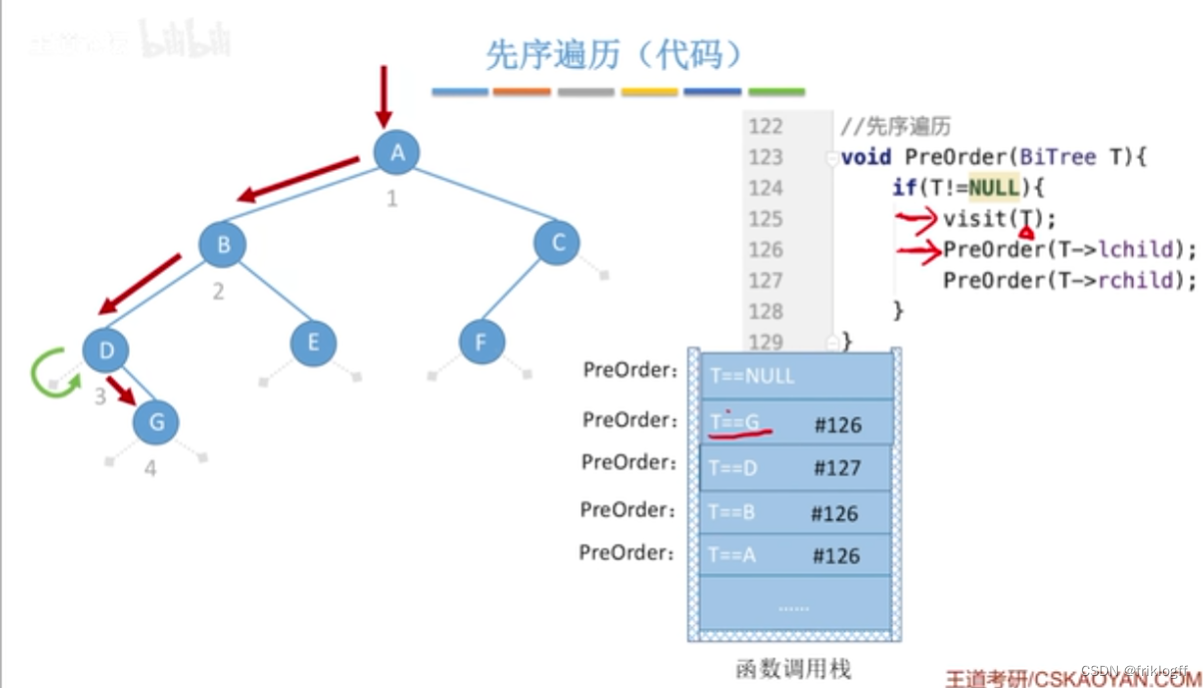
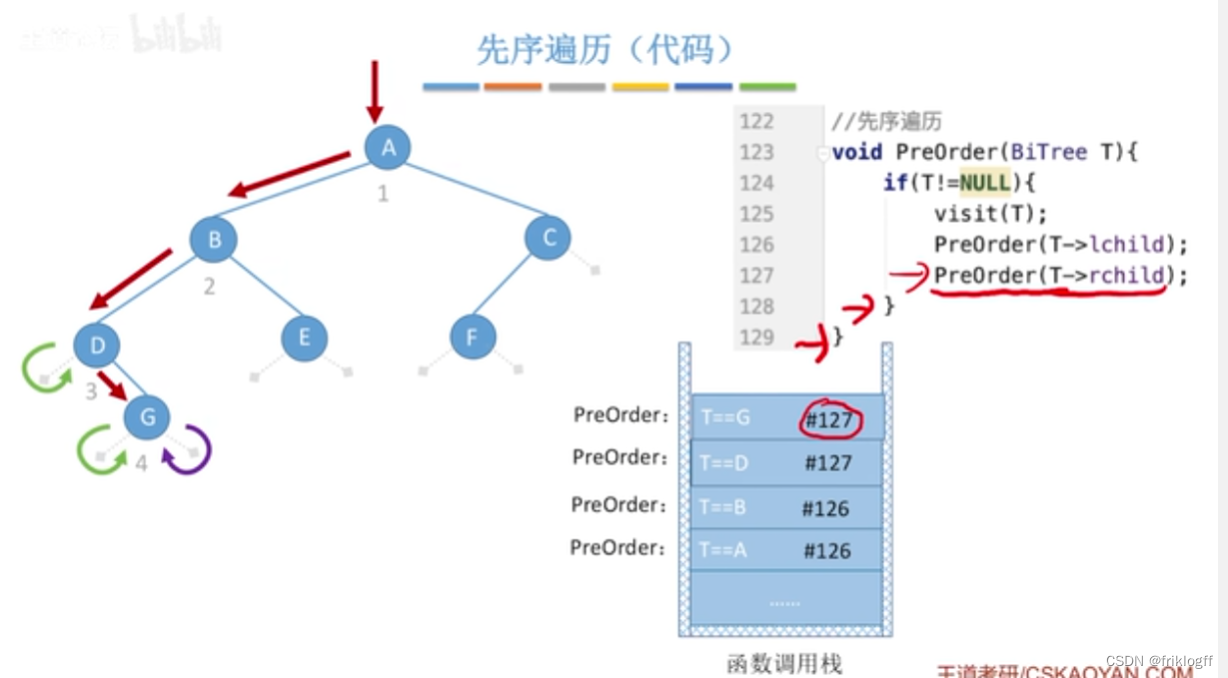
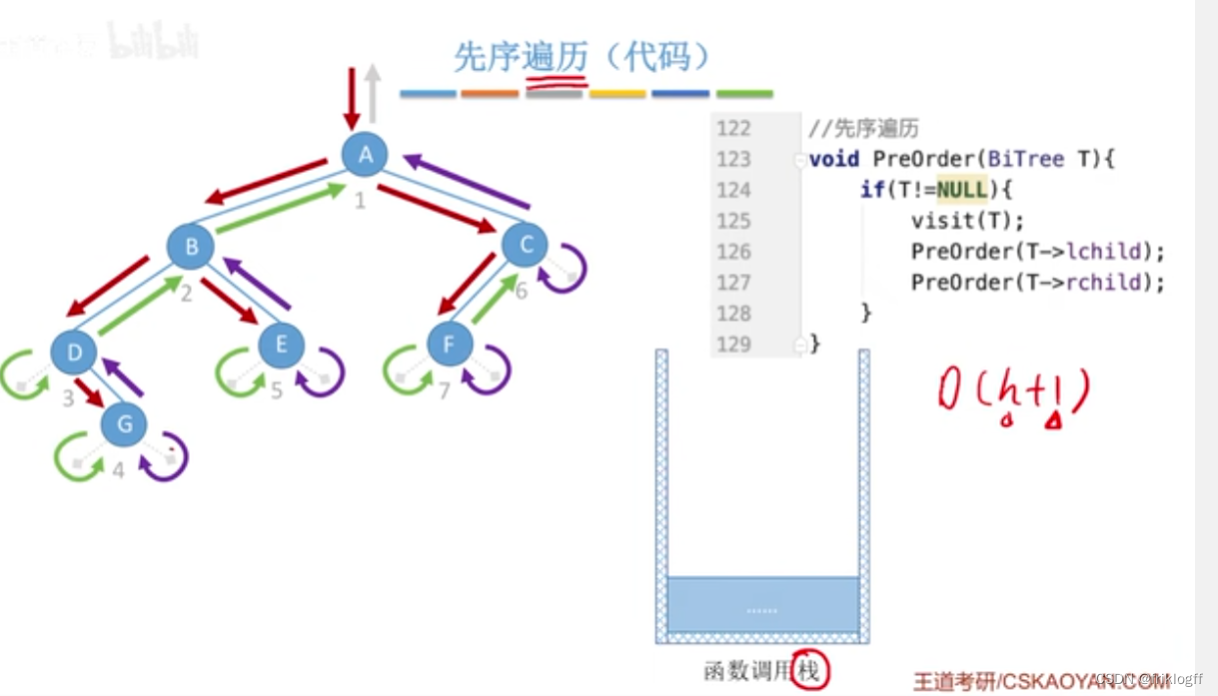
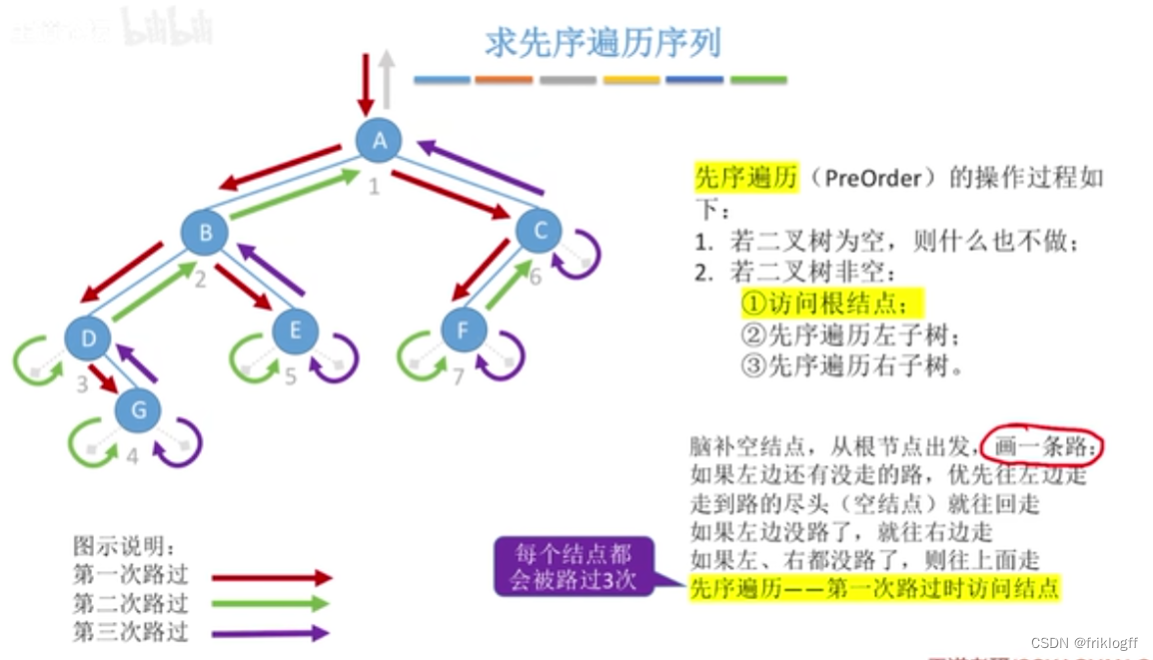
先序遍历

- 先访问根结点
- 先序遍历左子树
- 先序遍历右子树

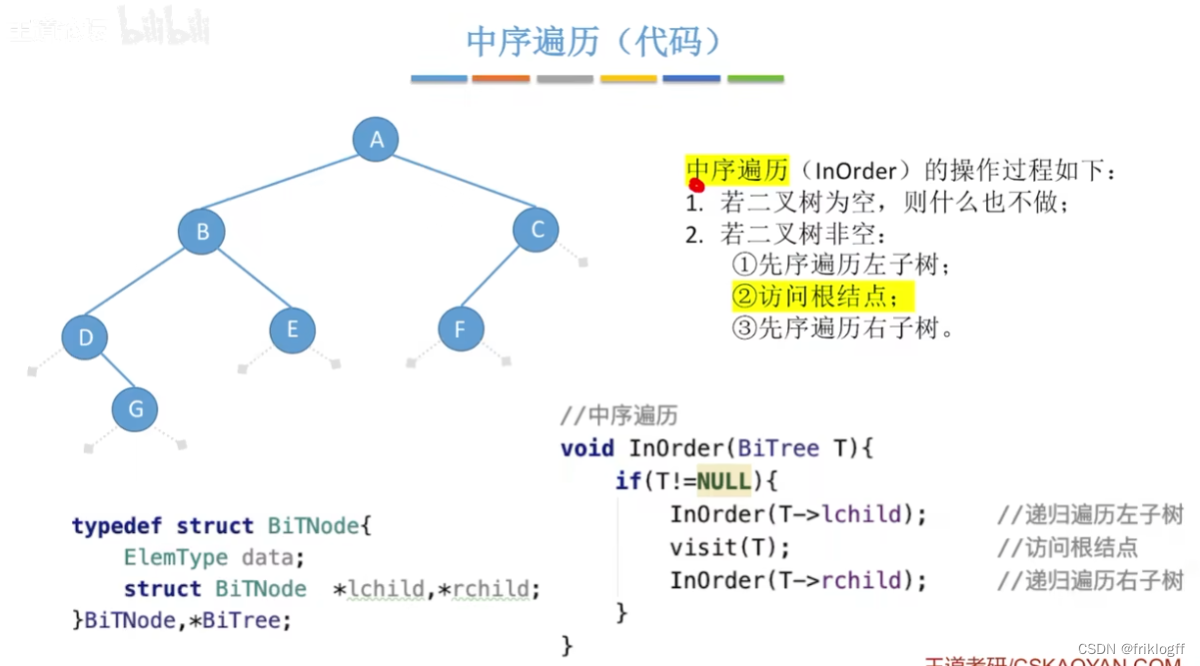
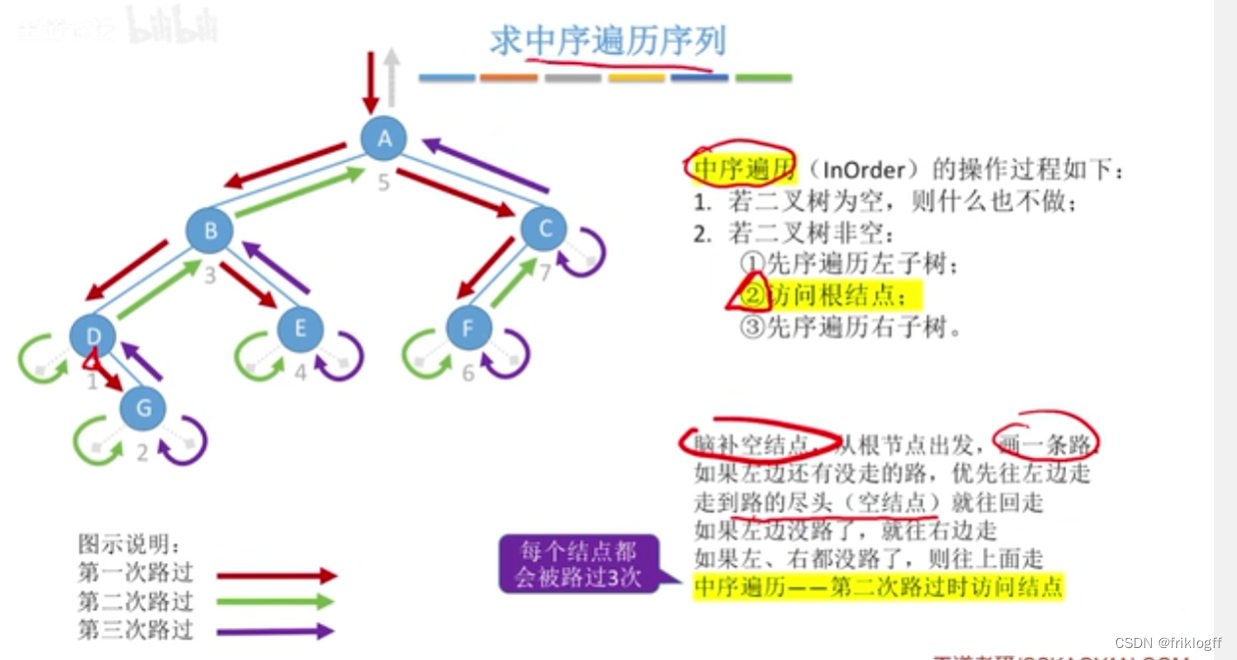
在这里插入图片描述

中序遍历

- 中序遍历左子树
- 访问根结点
- 中序遍历右子树

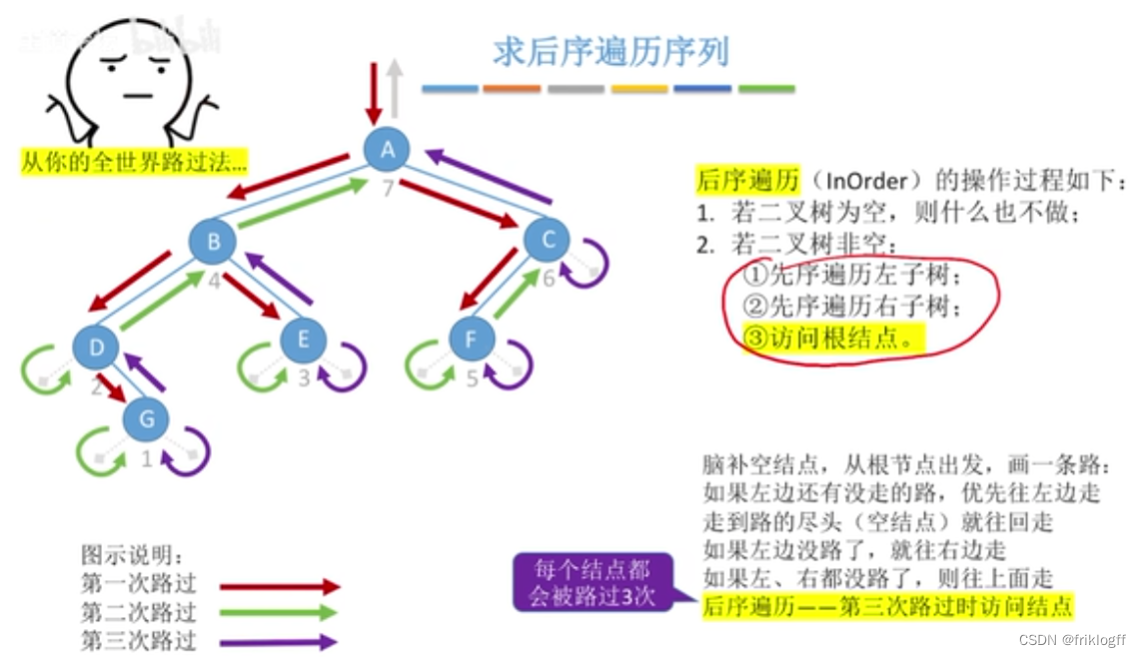
后序遍历

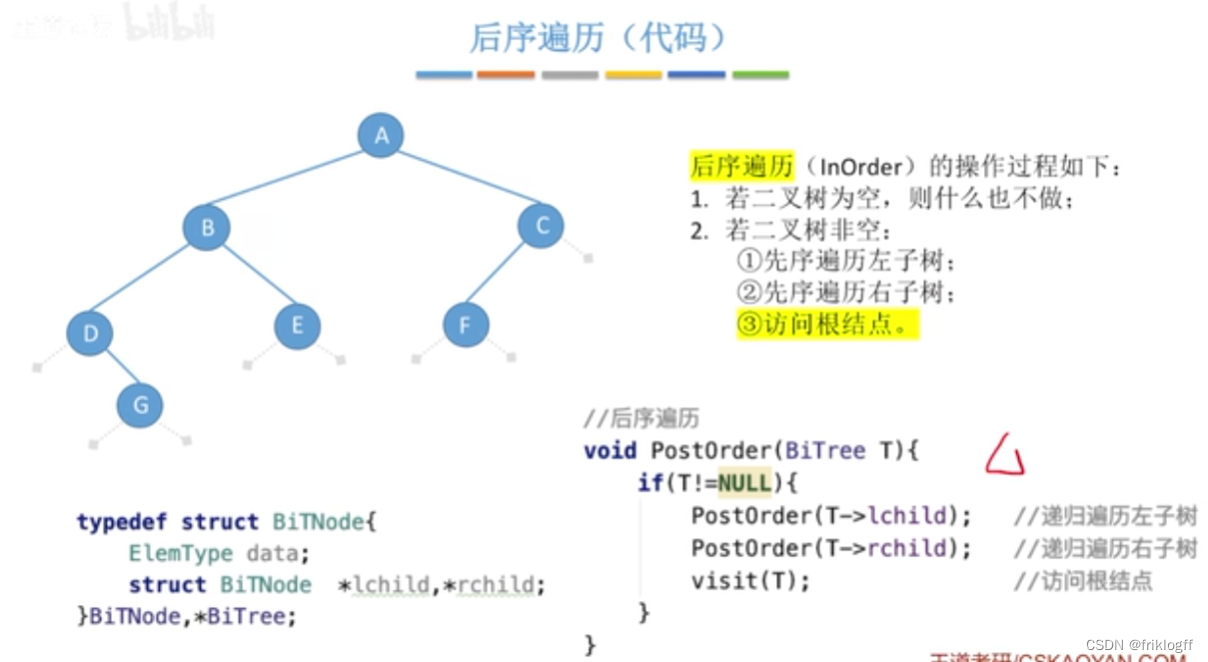
- 后序遍历左子树
- 后序遍历右子树
- 访问根结点
- 可用于找祖先和子孙结点间路径

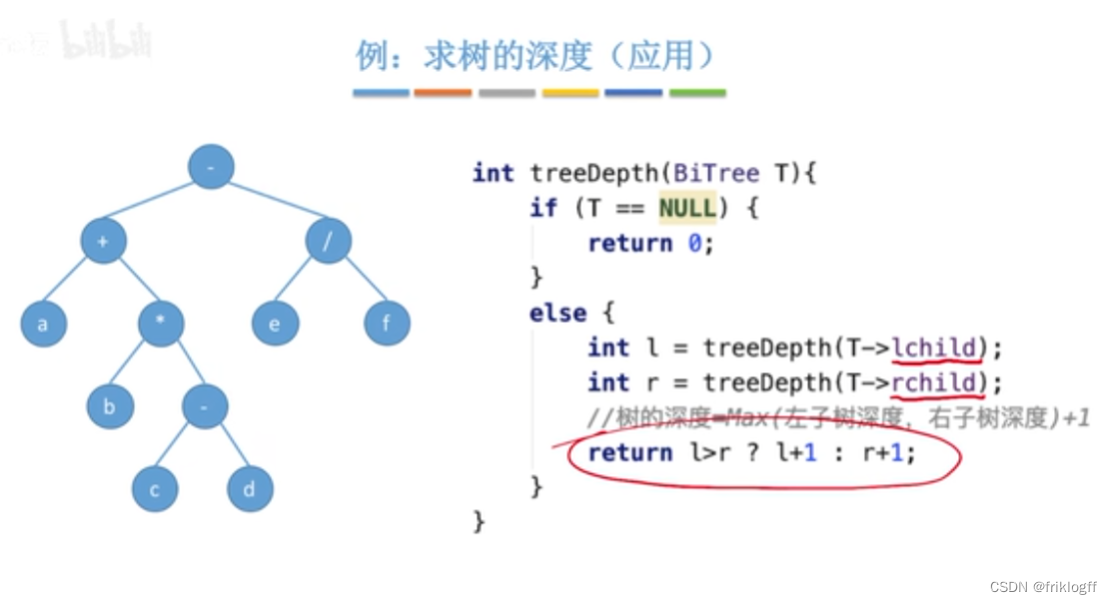
在这里插入图片描述

小结

在这里插入图片描述

层次遍历

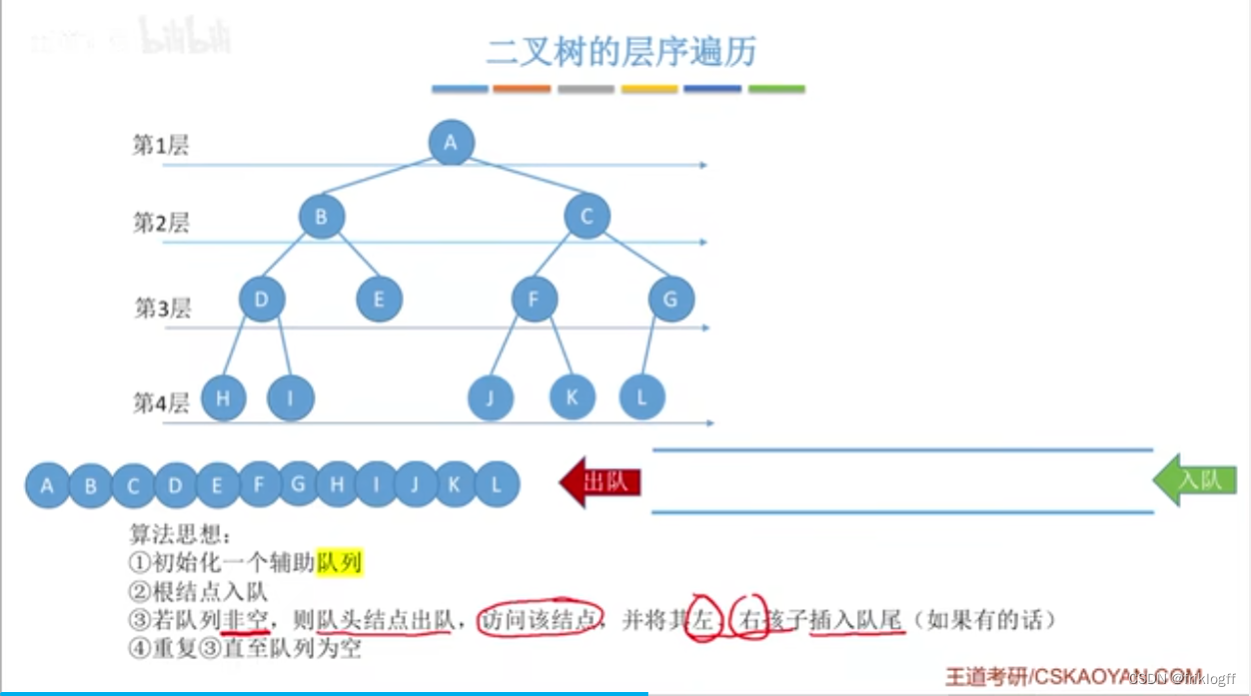
- 先将二叉树根结点入队，然后出队，访问出队结点
- 若它有左子树，则将左子树根结点入队
- 若它有右子树，则将右子树根结点入队
- 然后出队，访问出队结点…如此反复，直到队列为空

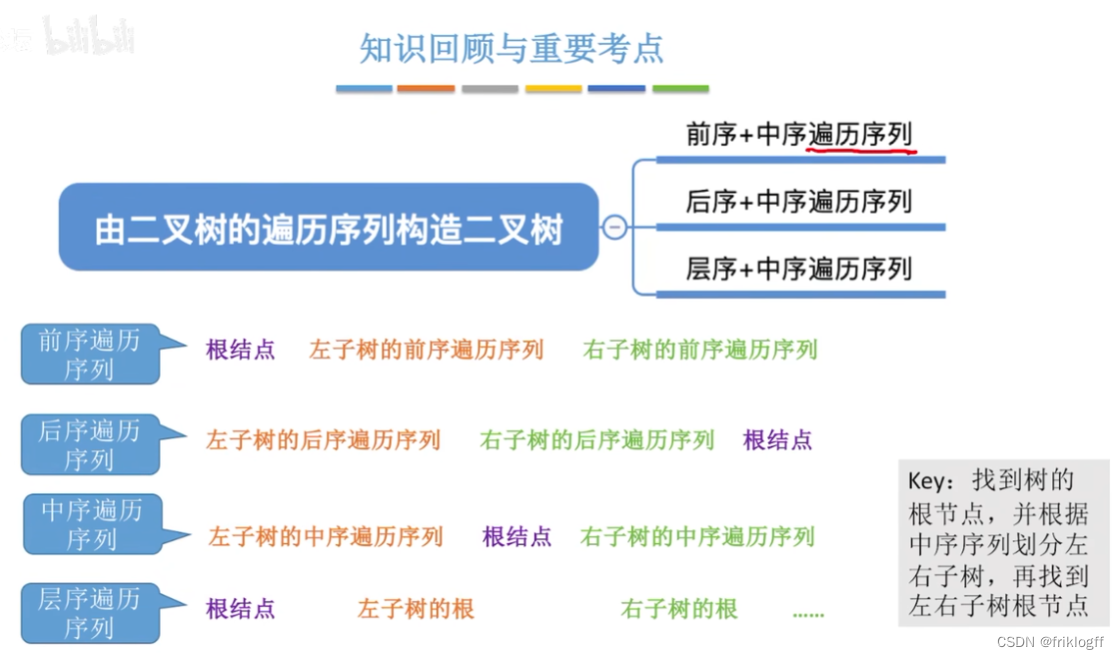
由遍历序列构造二叉树

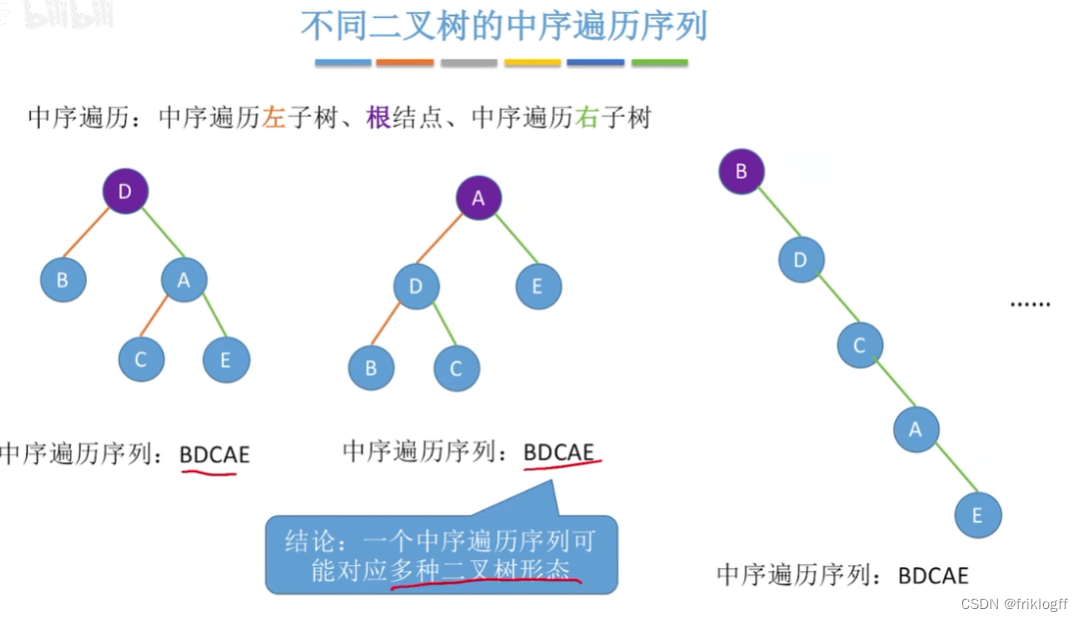
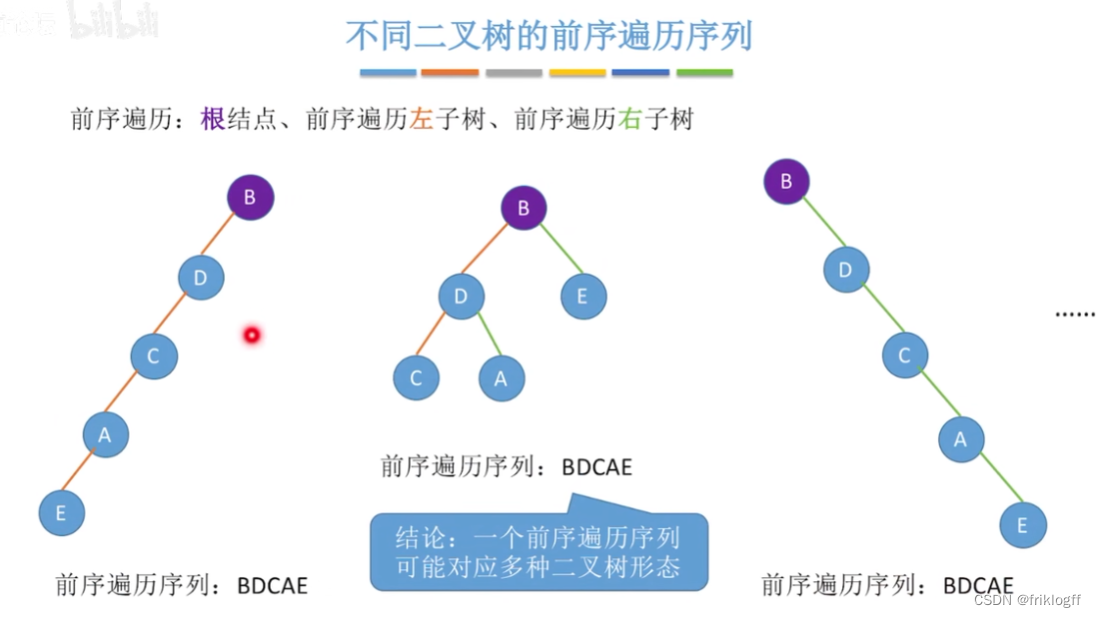
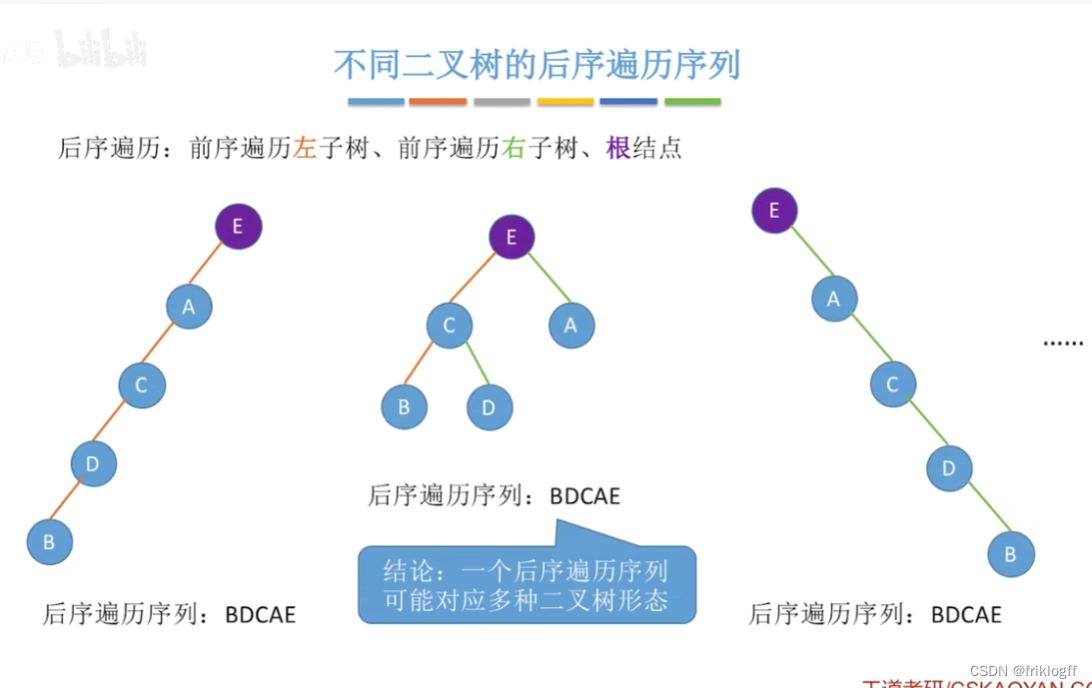
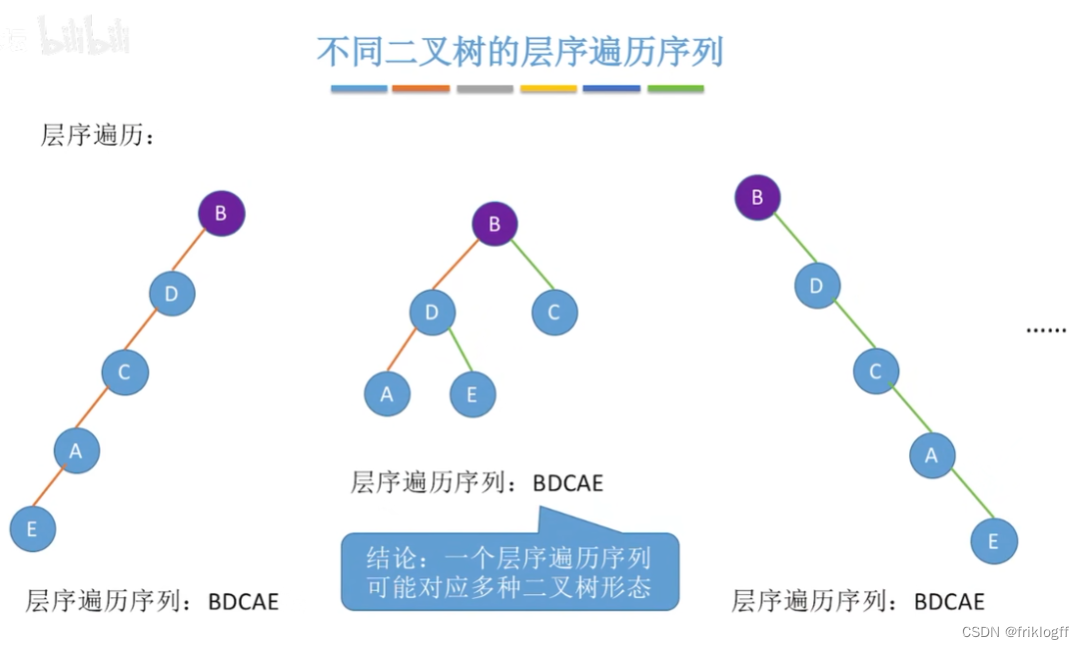
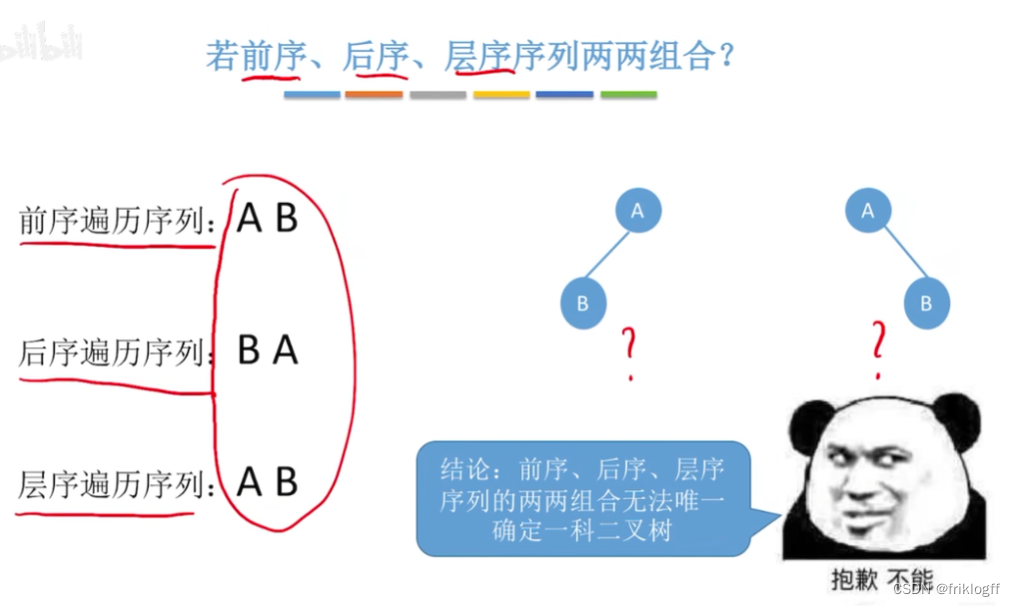
在这里插入图片描述

二叉树的先序（或后序）序列和中序序列可以唯一确定一颗二叉树

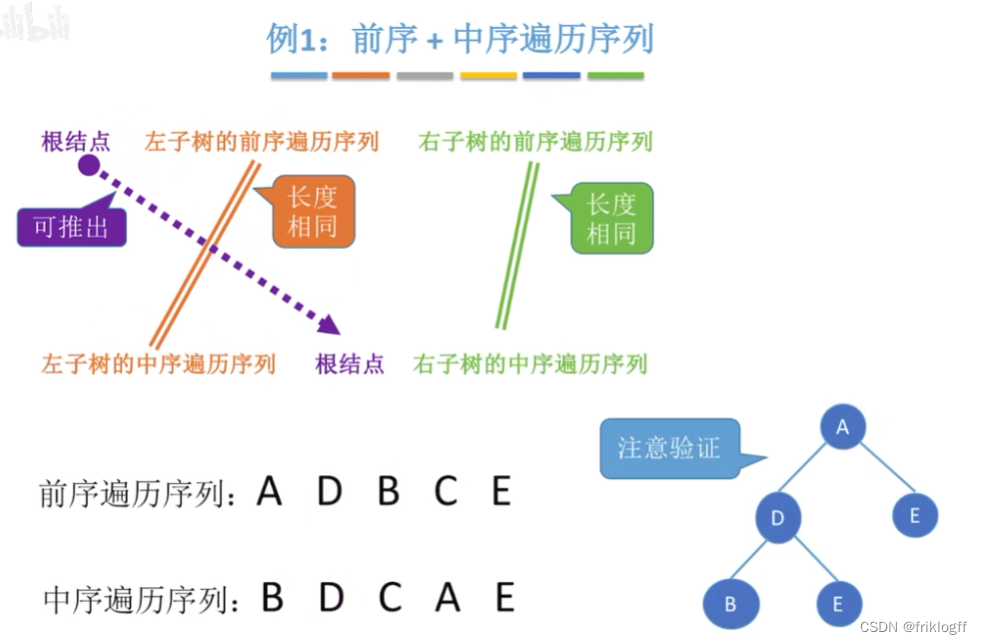
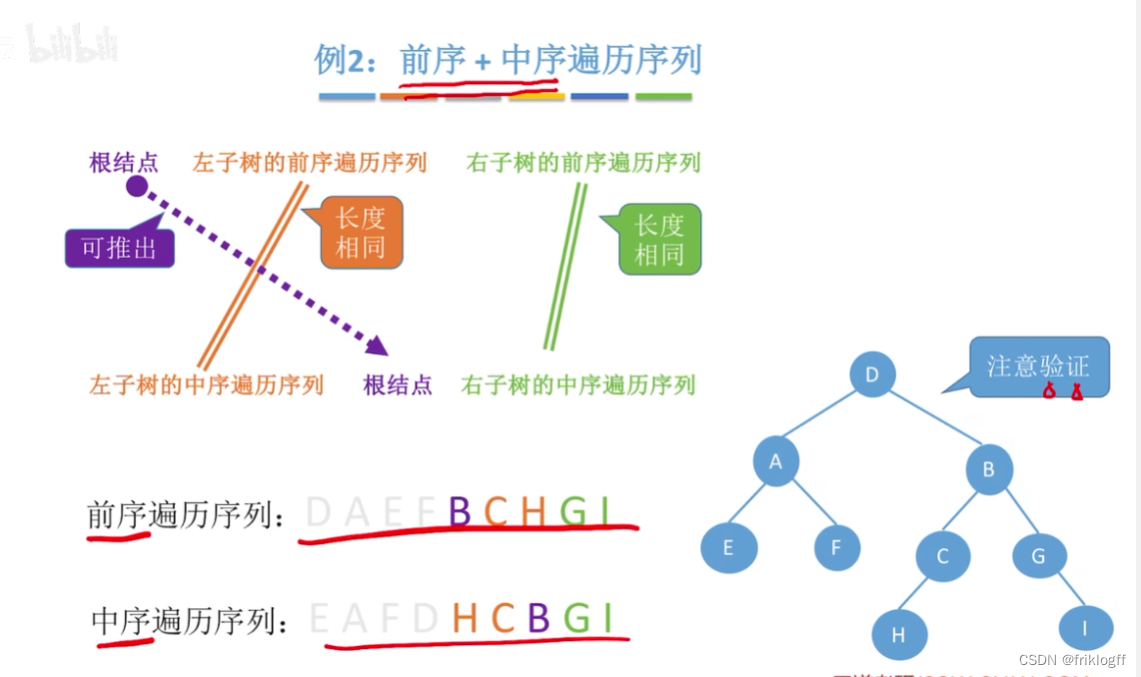
前序＋中序遍历序列

前序确定根节点（第一个出现的），中序确定左右子树

前序遍历序列=根结点+左子树的前序遍历序列+右子树的前序遍历序列

中序遍历=左子树的中序遍历序列+根结点+右子树的中序遍历序列

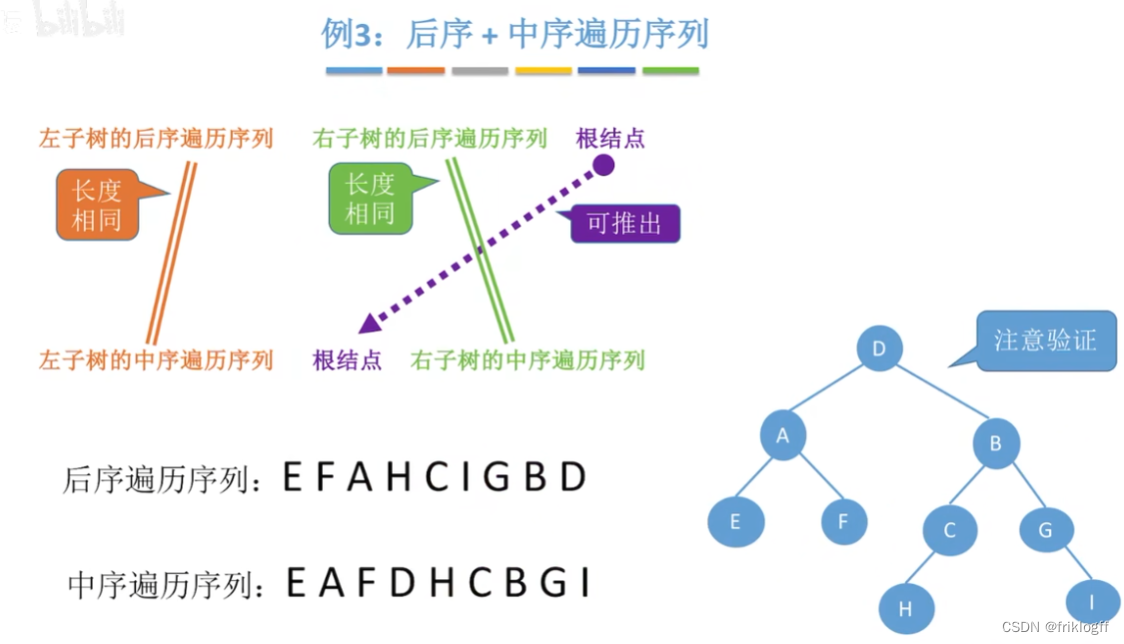
在这里插入图片描述

后序＋中序遍历序列

后序确定根节点（最后一个出现的），中序确定左右子树

后序遍历序列=左子树的后序遍历序列+右子树的后序遍历序列+根结点

中序遍历=左子树的中序遍历序列+根结点+右子树的中序遍历序列

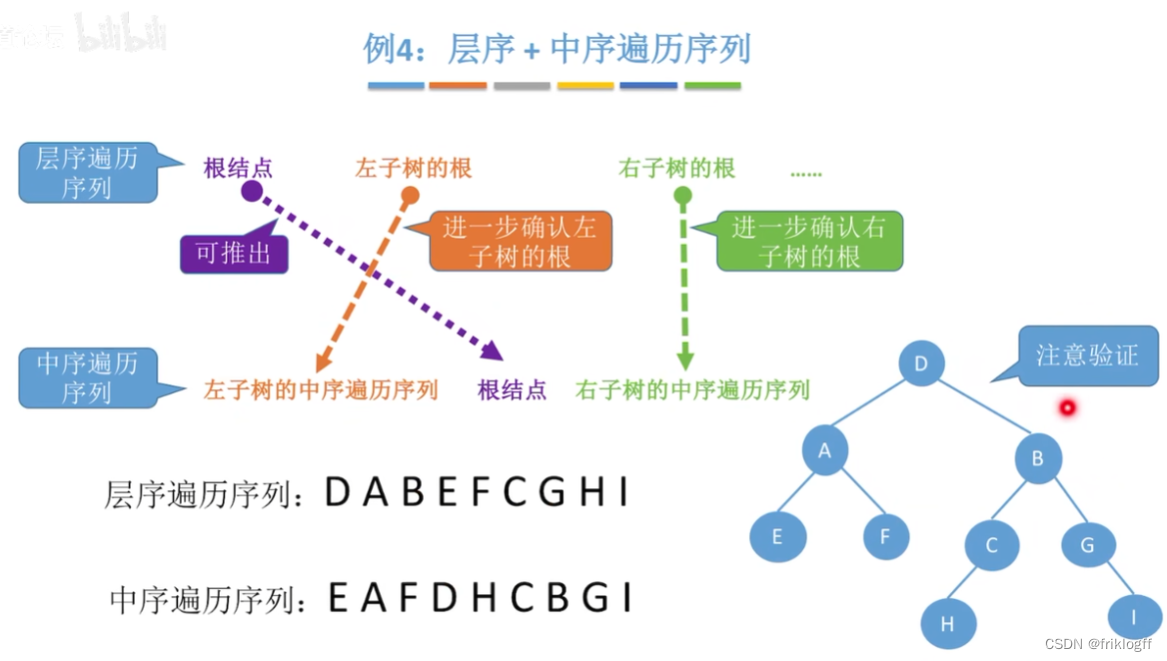
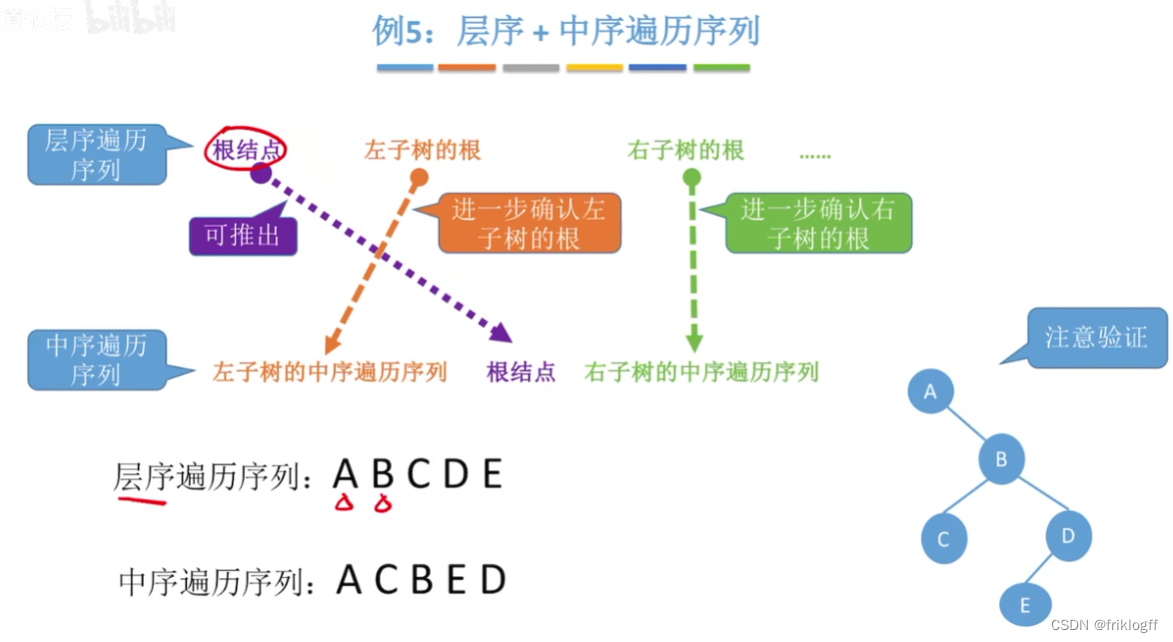
在这里插入图片描述

层序＋中序遍历序列

层序确定根节点（第一个出现的），中序确定左右子树

中序遍历=左子树的中序遍历序列+根结点+右子树的中序遍历序列

层序遍历=根结点+左子树的根+右子树的根

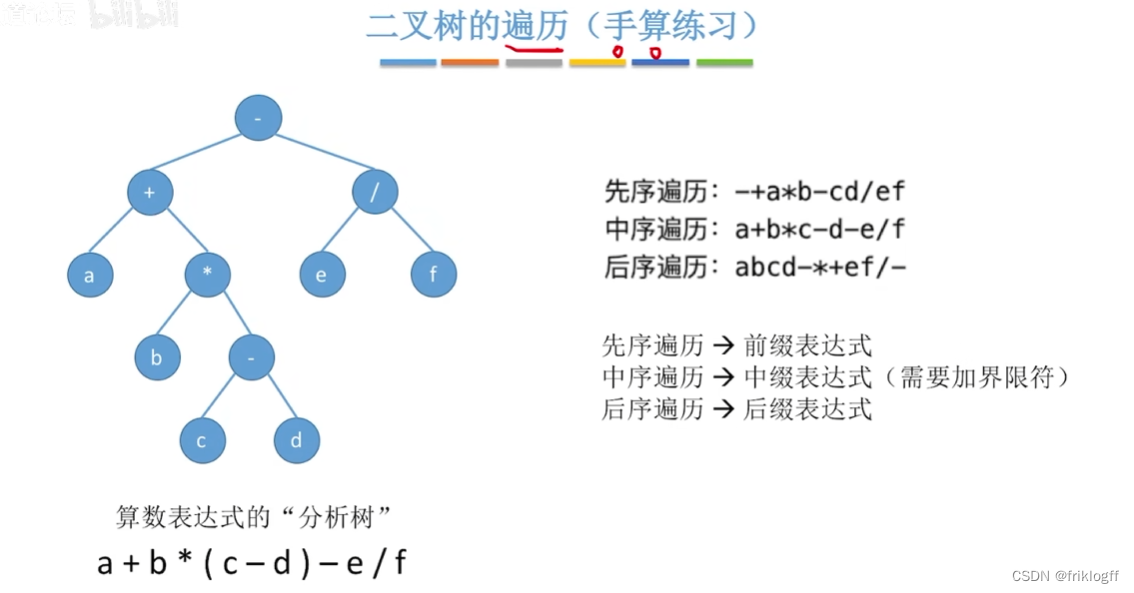
在这里插入图片描述

用二叉树表示算术表达式，将算术表达式转变为二叉树
先序遍历对应前缀表示
中序遍历对应中缀表示
后序遍历对应后缀表示
递归算法和非递归算法的转换：利用栈进行实现

小结

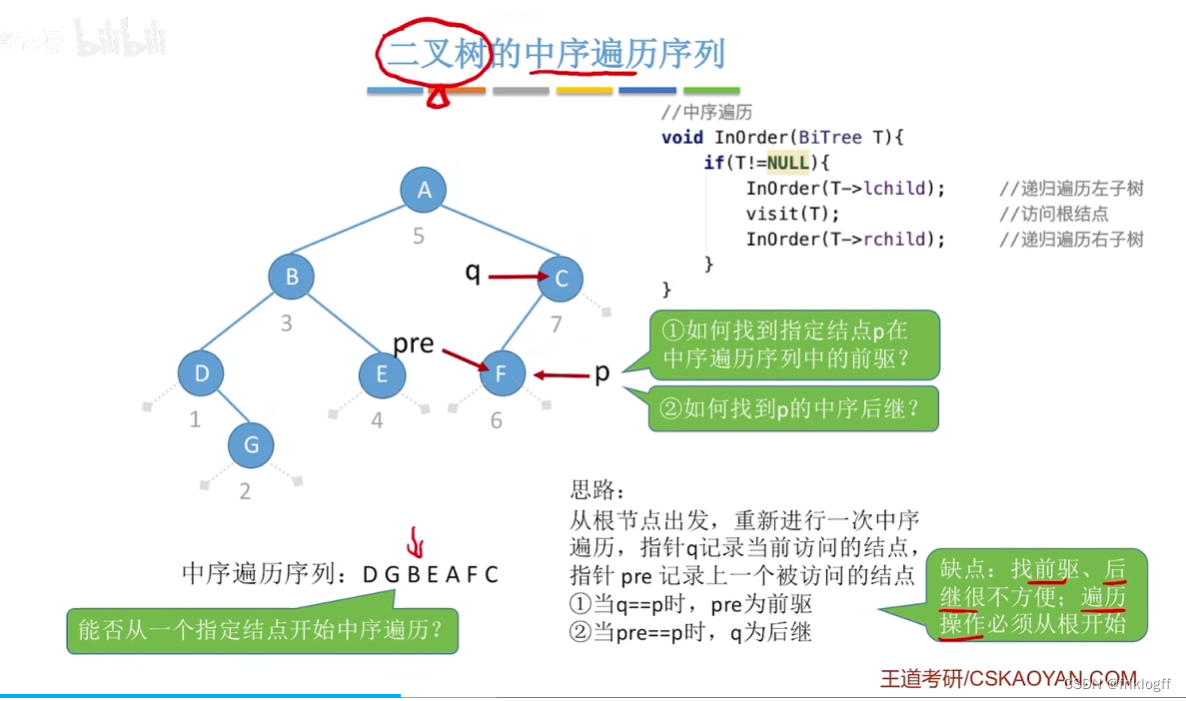
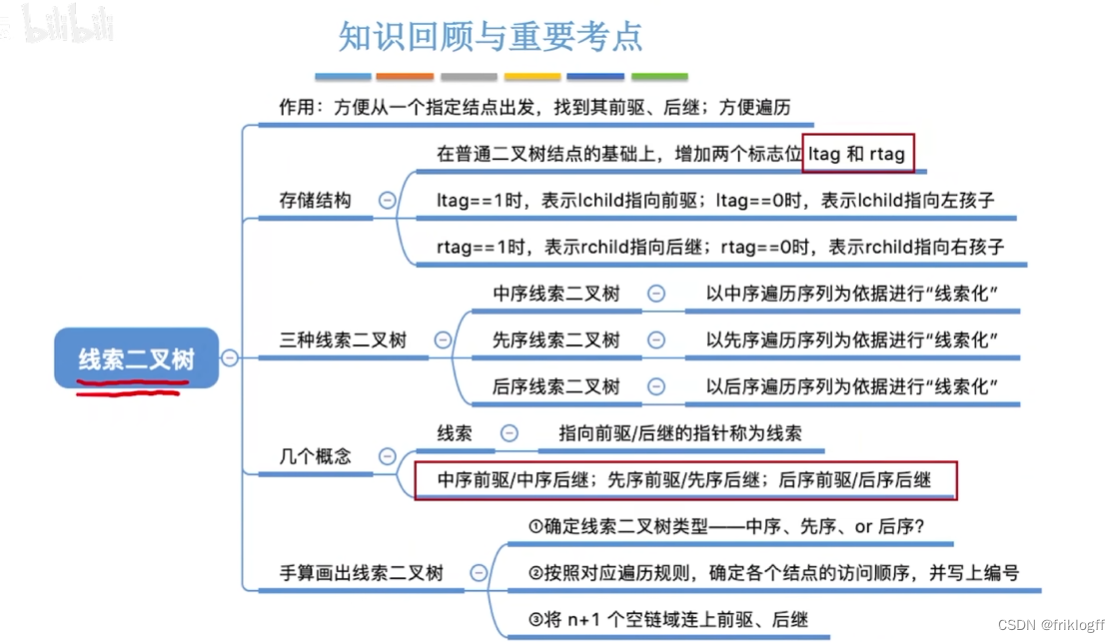
在这里插入图片描述

线索二叉树

在这里插入图片描述

概念
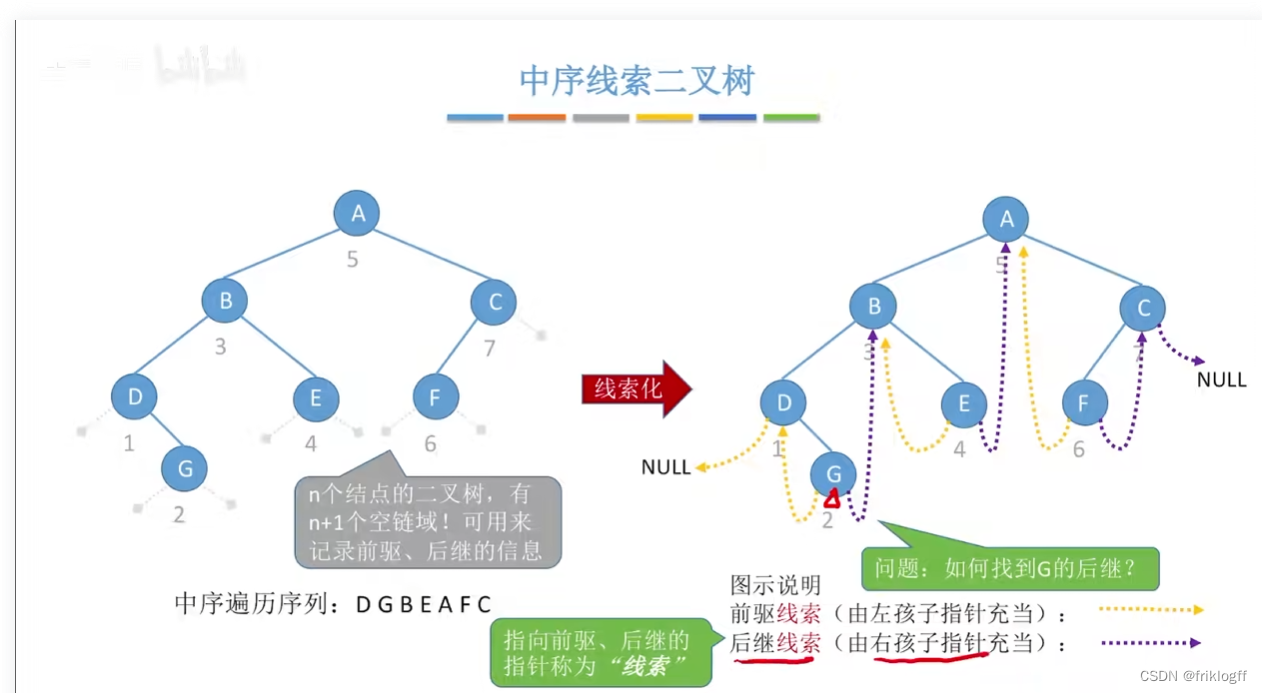
- 将结点空的指针指向其前驱和后继，这种改变指向的指针称为“线索”，加上线索的二叉树称为线索二叉树
  - 方便找到前驱和后继
  - 遍历可以不从根结点开始
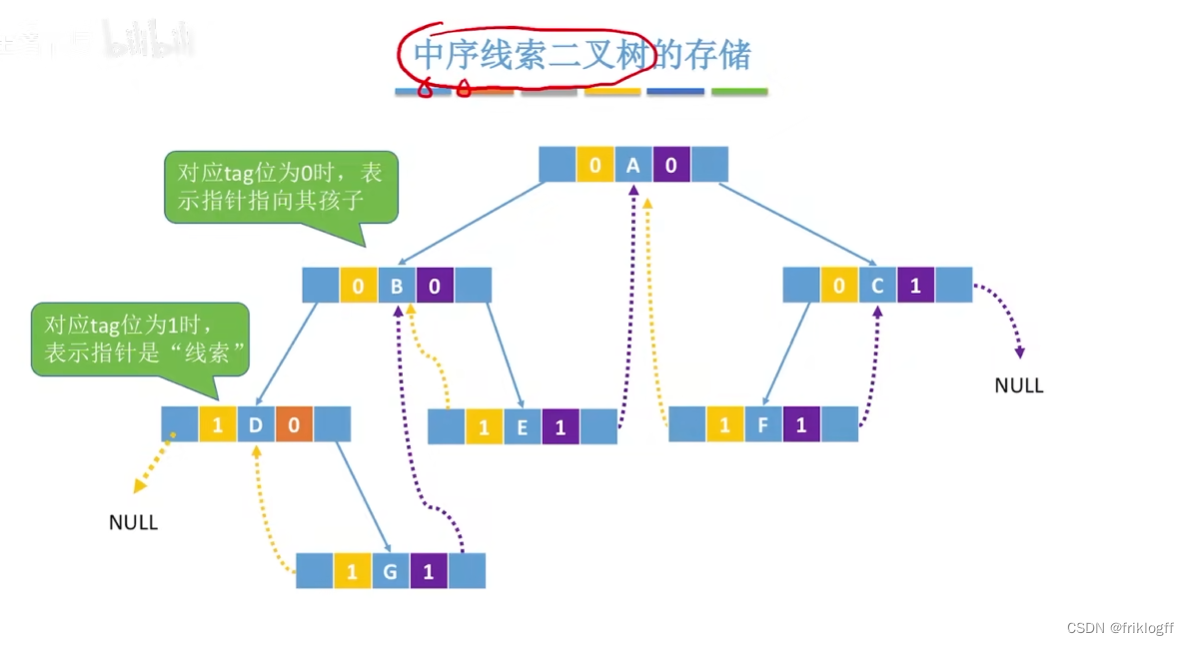
- 一种物理结构
  - 二叉树内部的存储结构
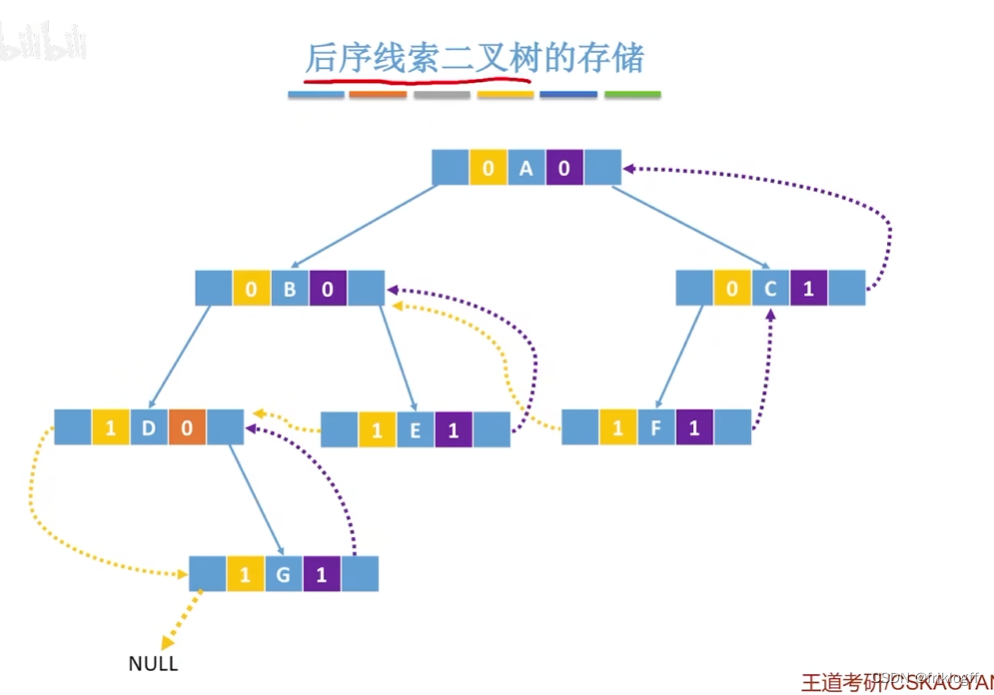
结构
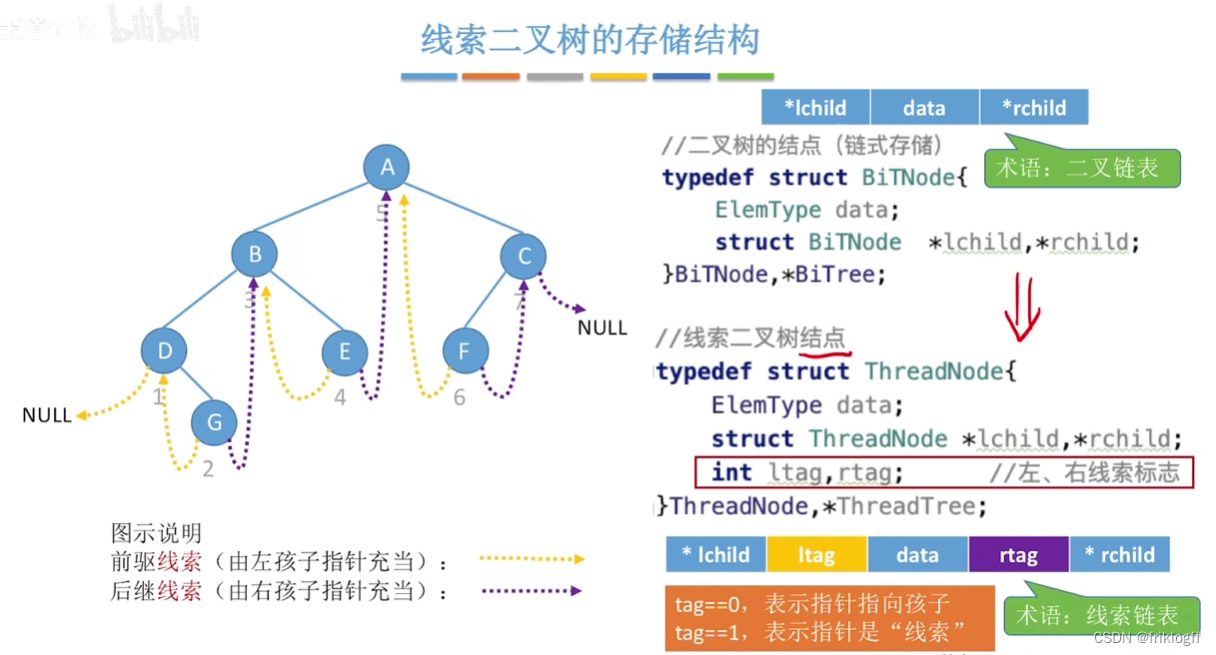
- - 1表线索，0表孩子
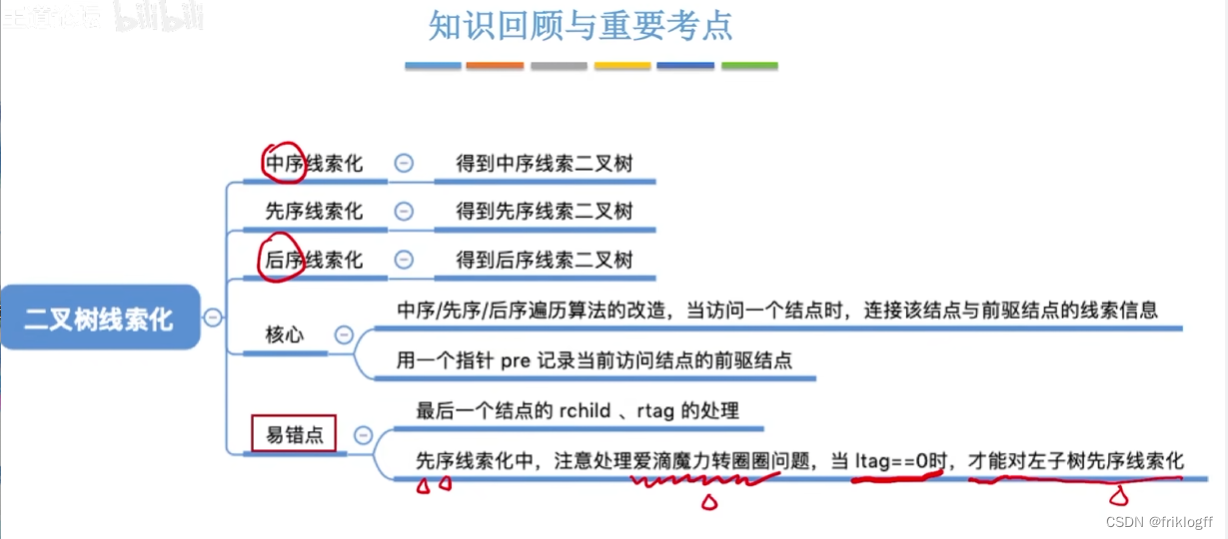
线索二叉树的构造
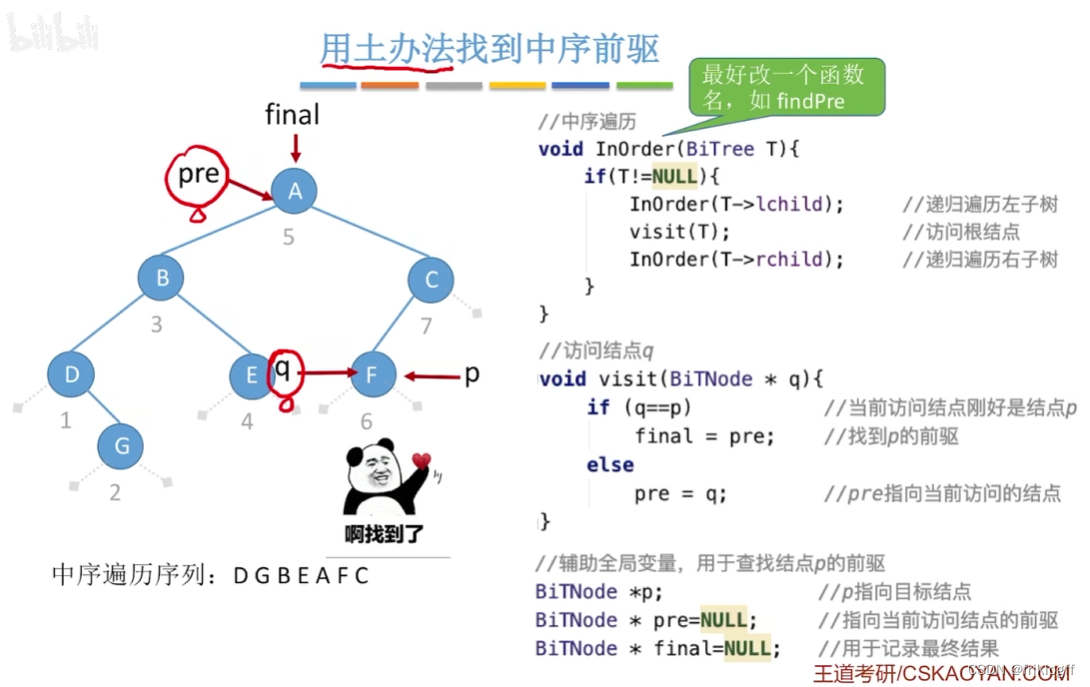
- 可以通过设置指针pre指向刚刚访问过的结点，指针p指向正在访问的结点，即pre指向p的前驱，从而找到前驱位置
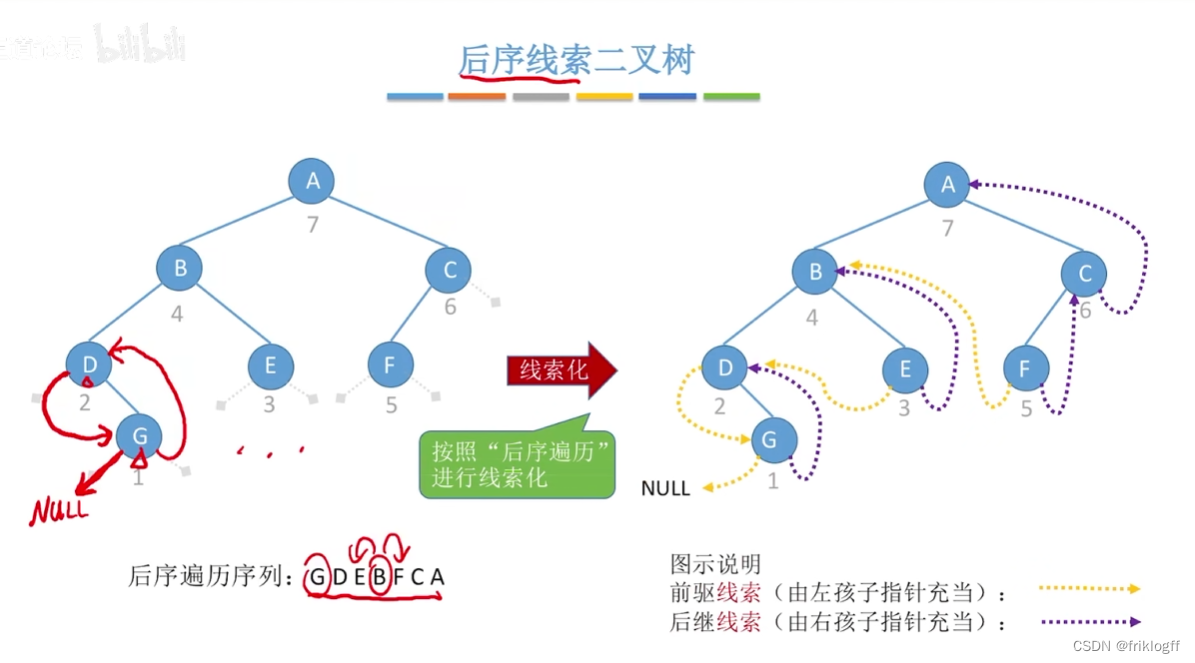
后序线索二叉树不能有效求后序后继

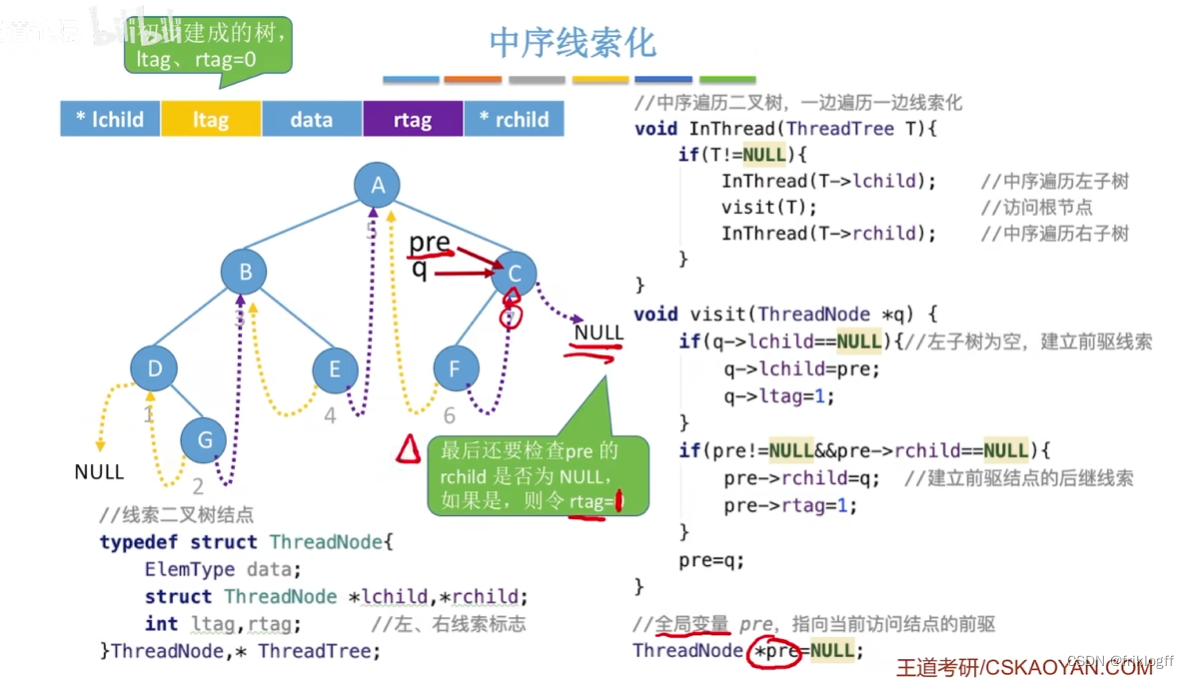
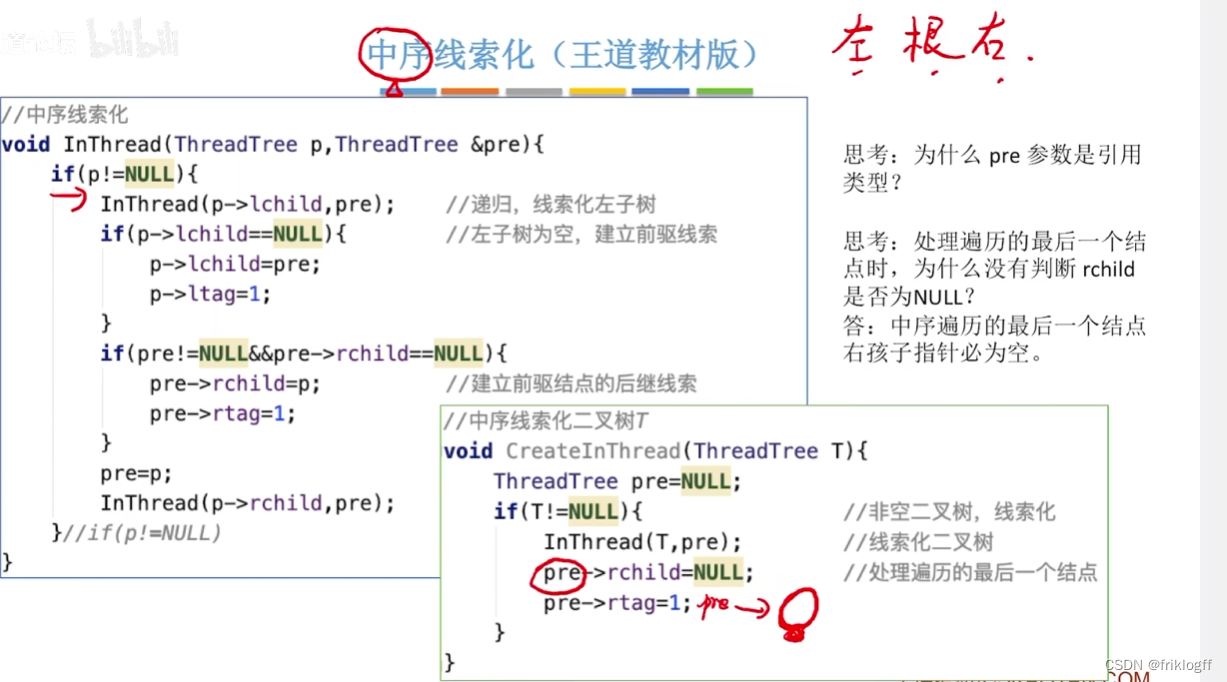
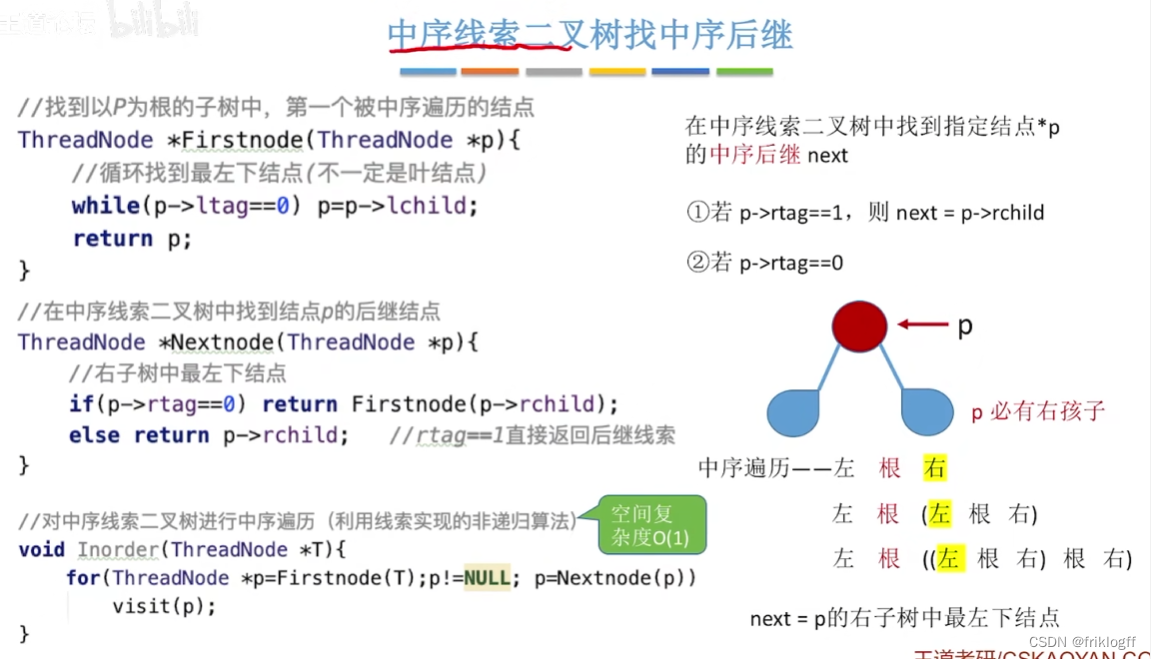
中序线索二叉树

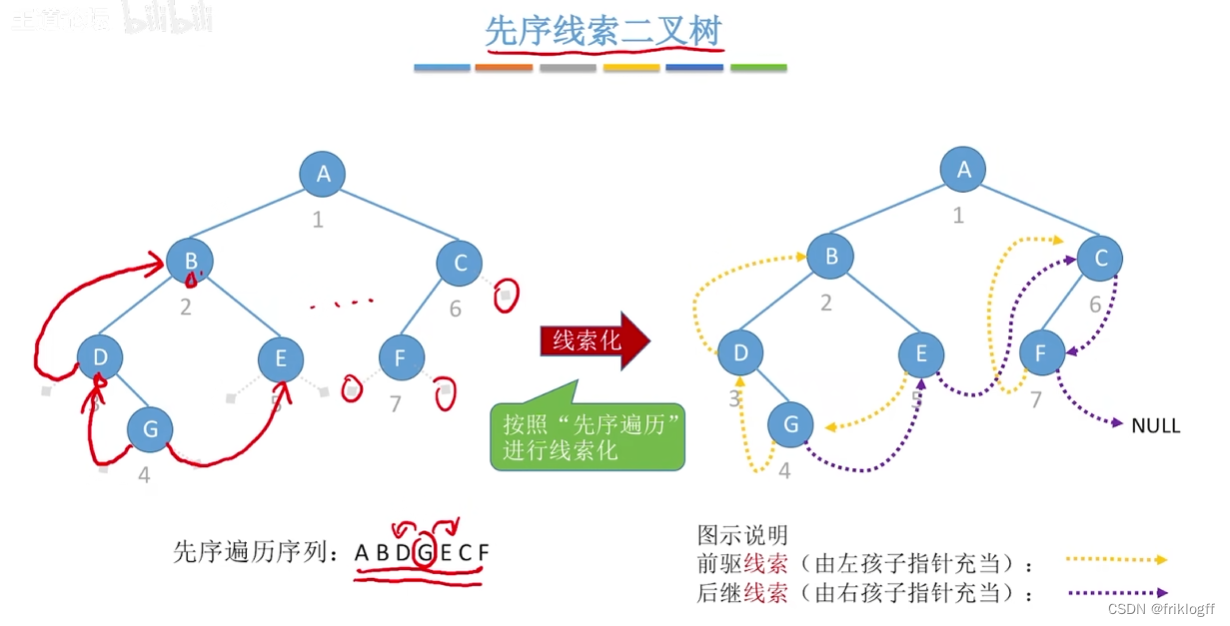
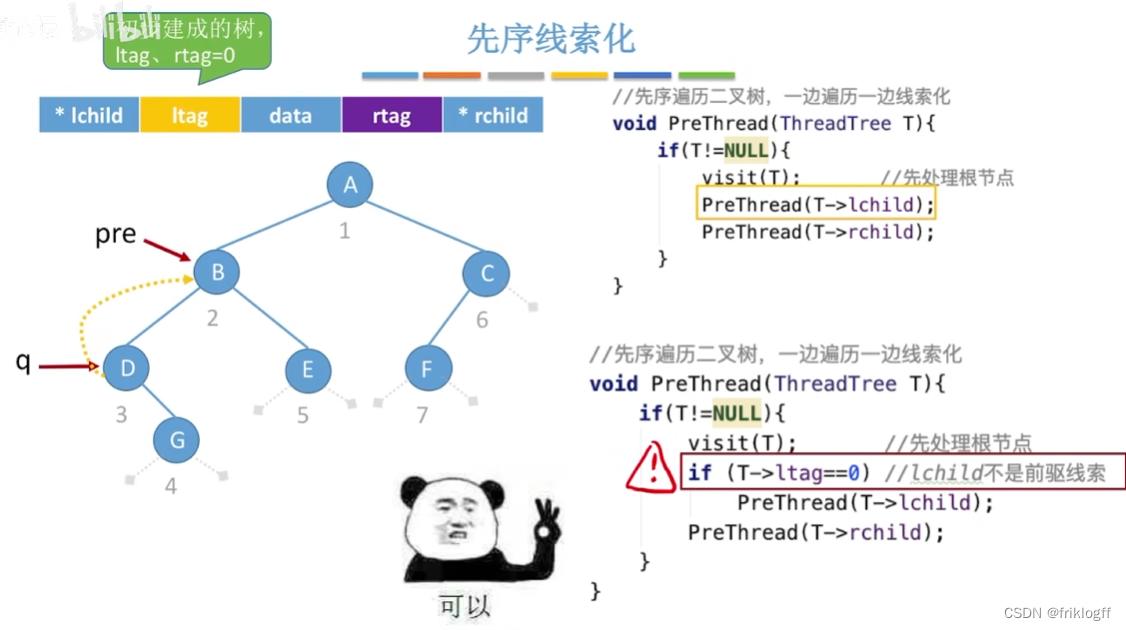
在这里插入图片描述

代码实现

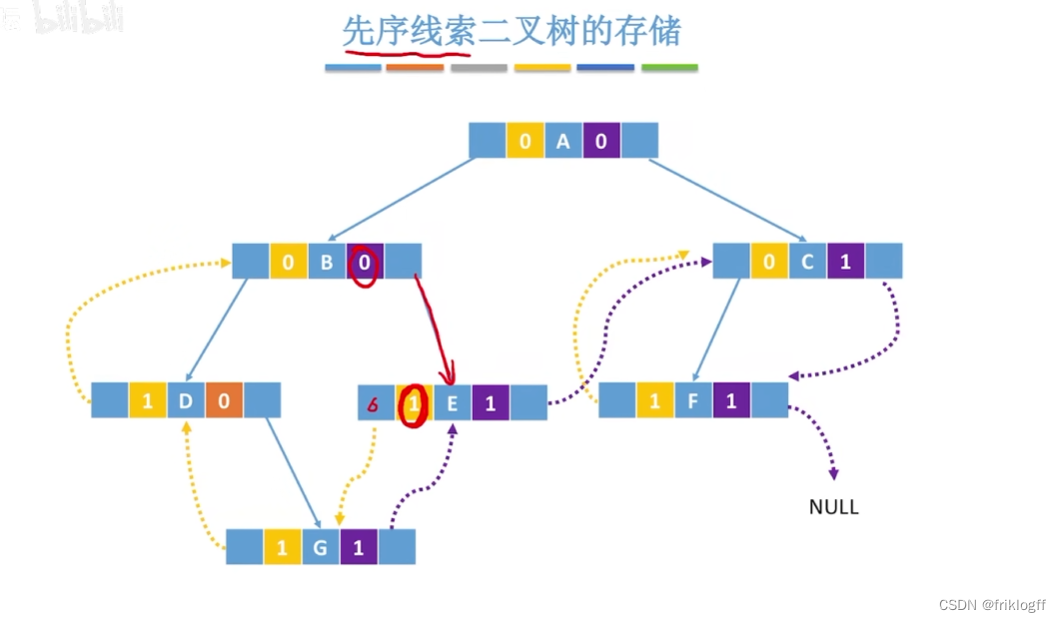
在这里插入图片描述

先序线索二叉树

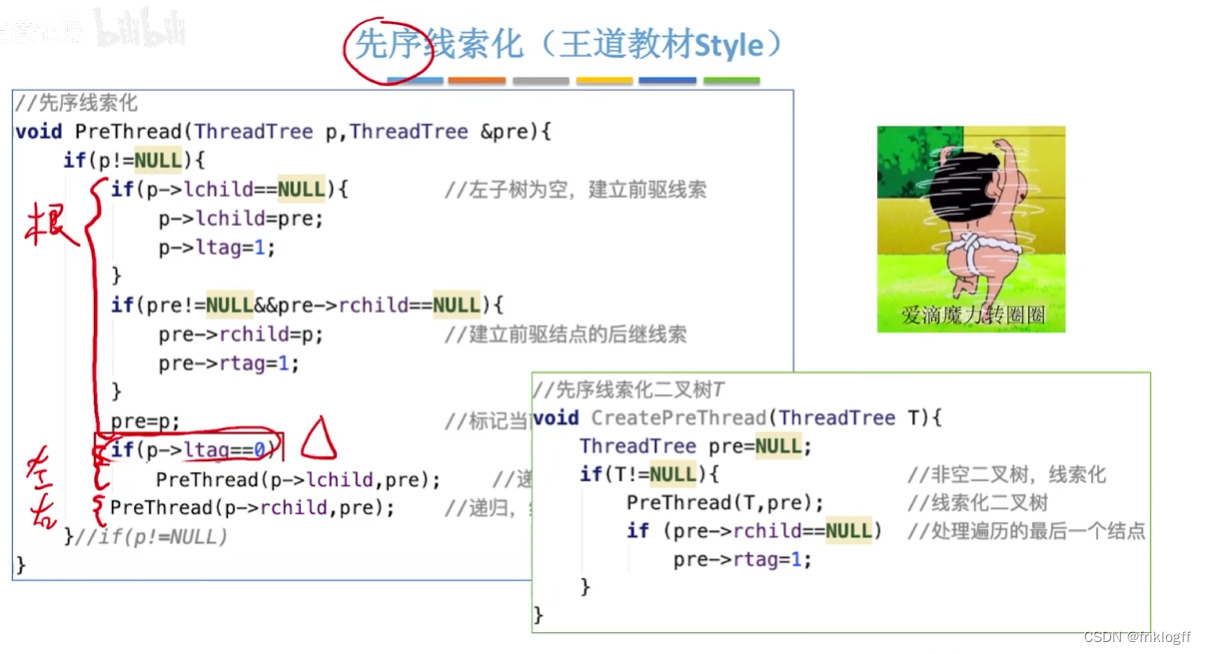
在这里插入图片描述

代码实现

不同点
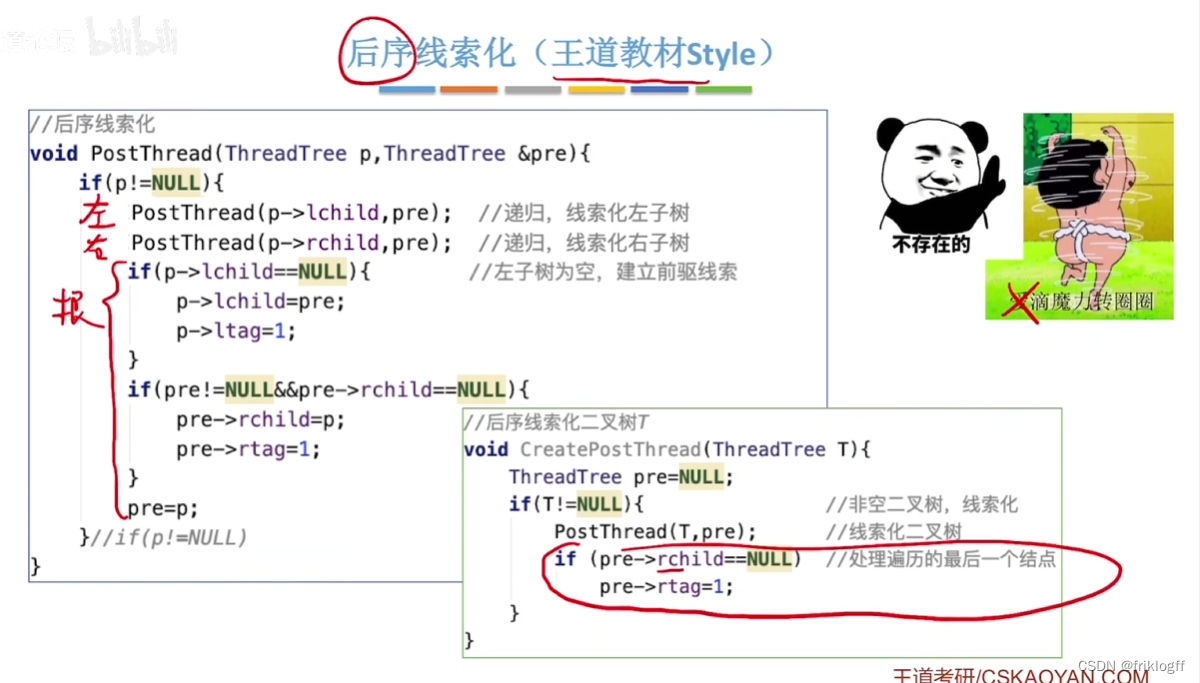
在这里插入图片描述

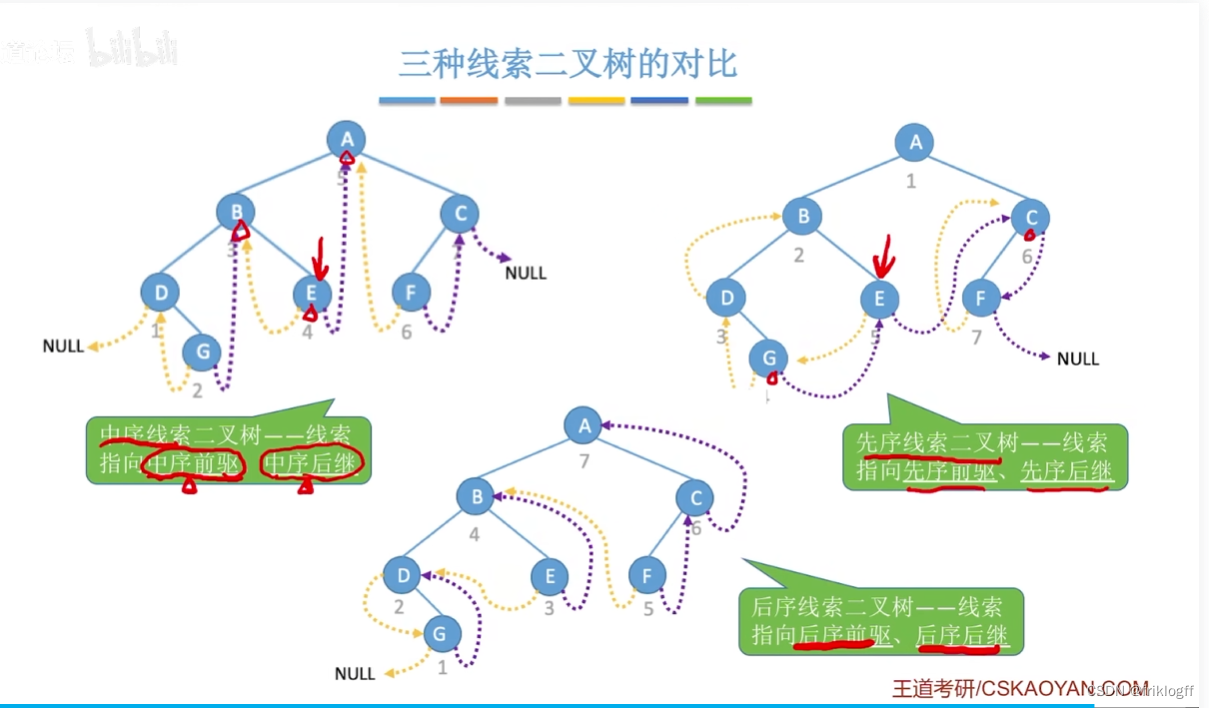
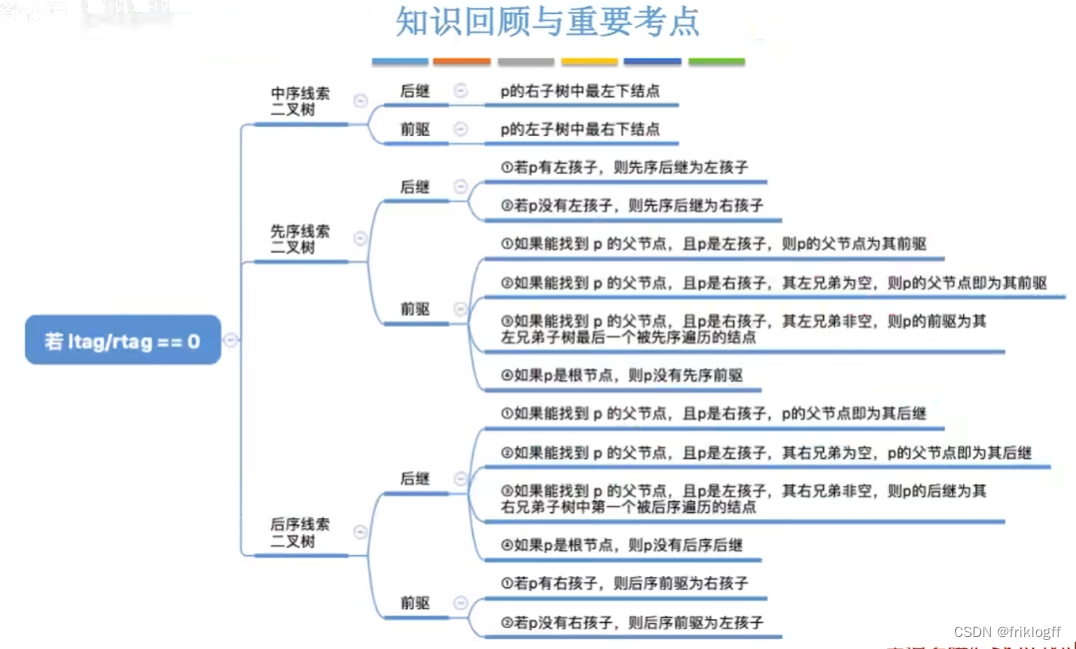
在这里插入图片描述

后序线索二叉树

在这里插入图片描述

代码实现

在这里插入图片描述

小结

在这里插入图片描述

线索二叉树找前驱/后继

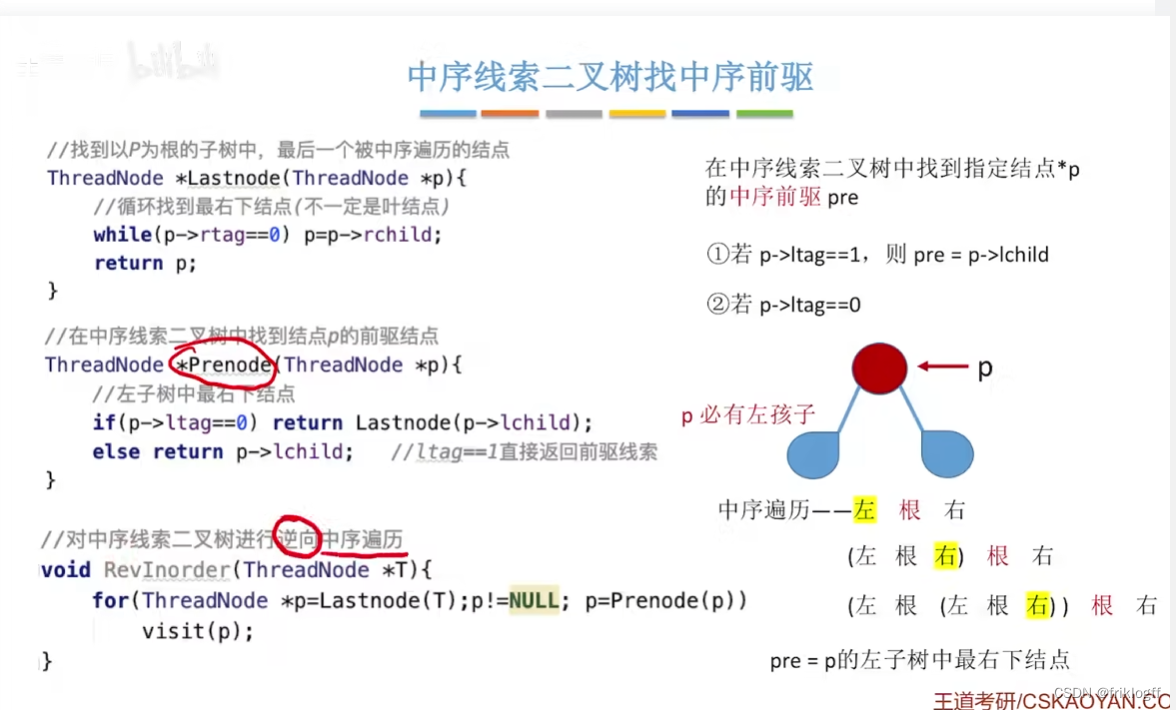
中序线索二叉树找中序后继

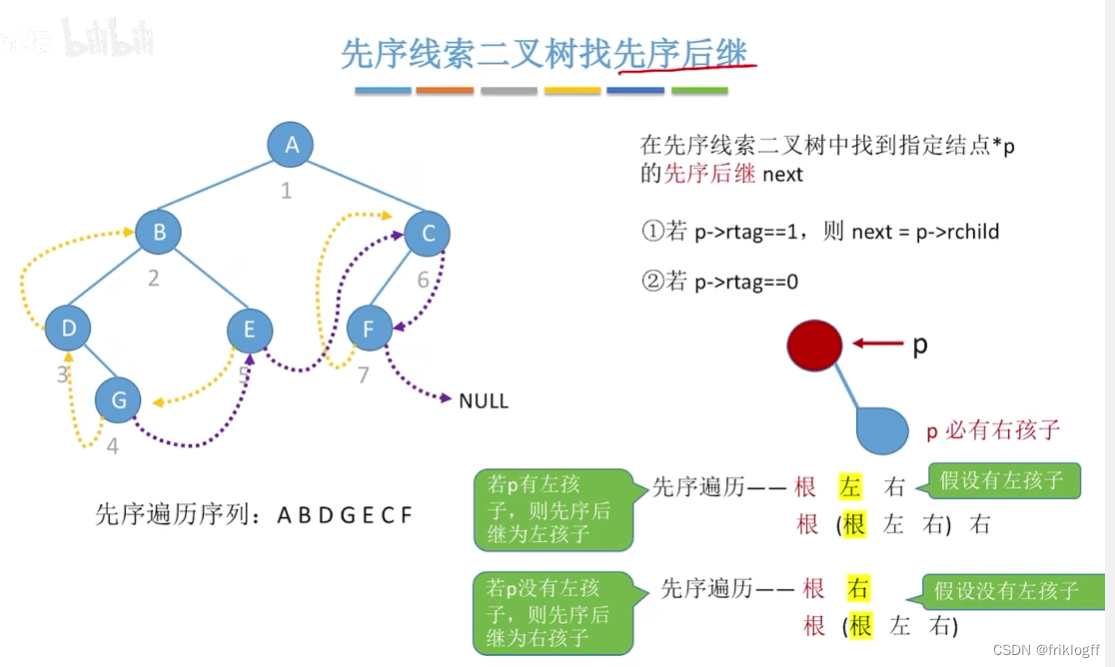
在这里插入图片描述

中序线索二叉树找中序前驱

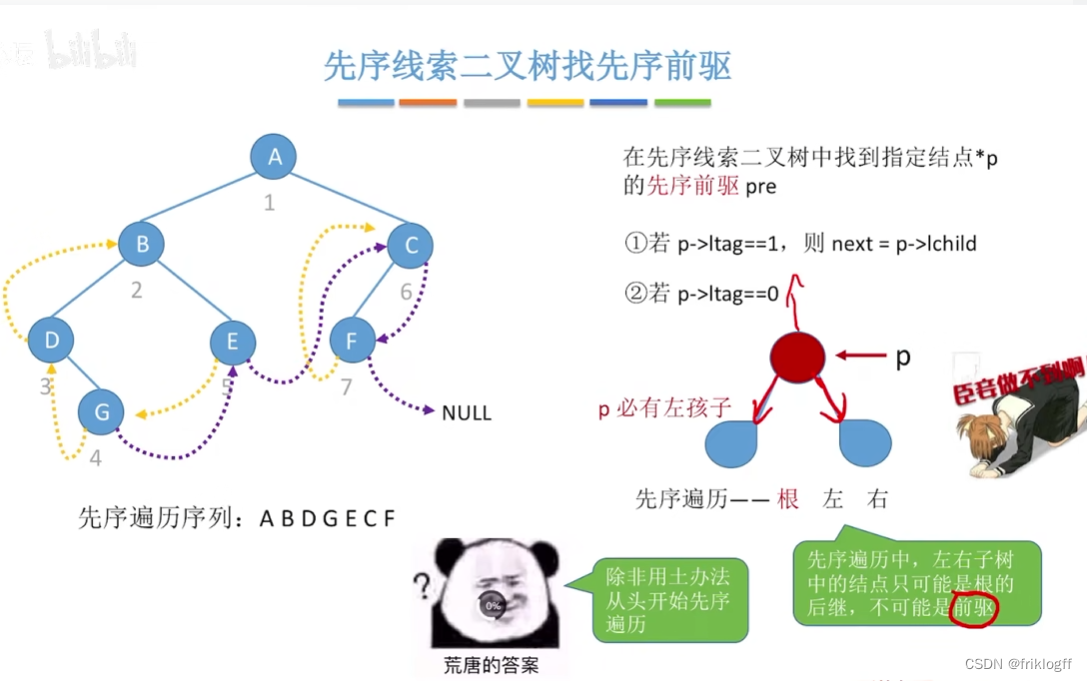
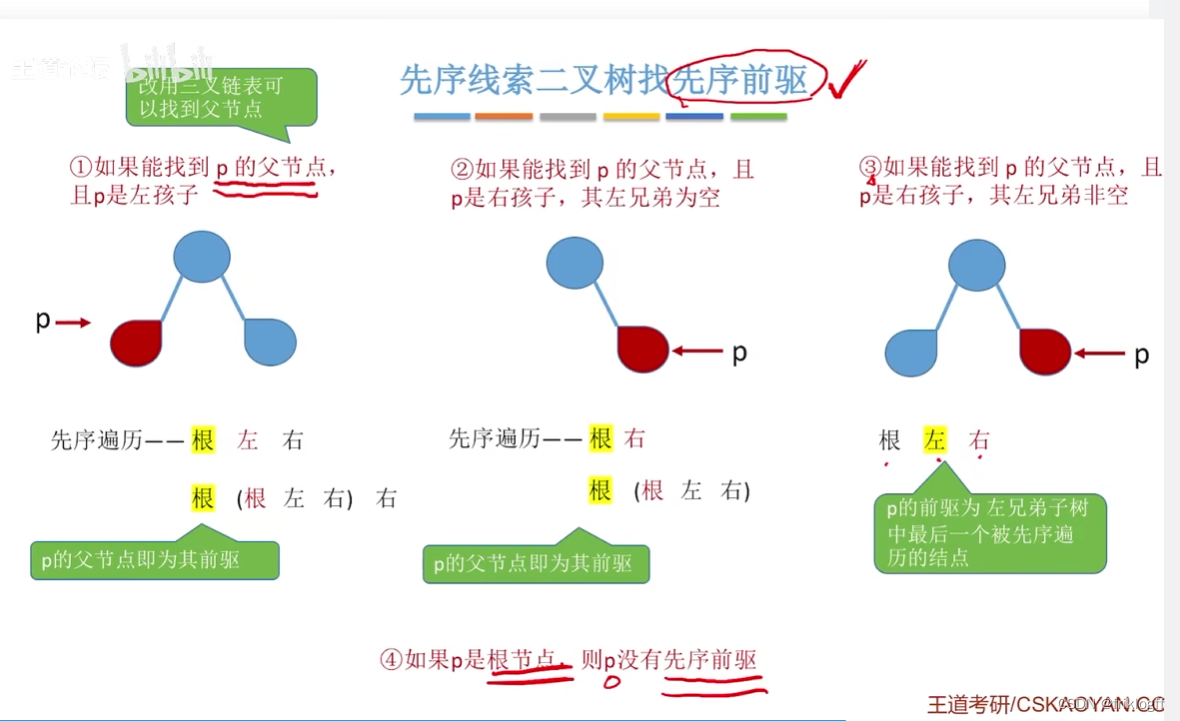
在这里插入图片描述

先序线索二叉树找中序后继

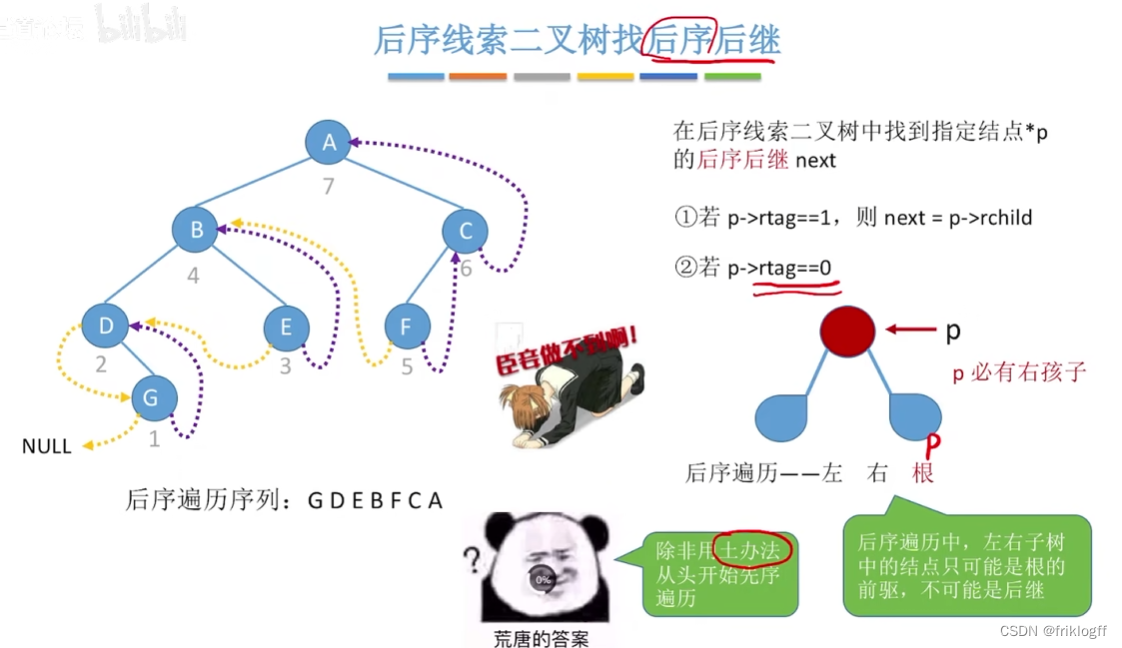
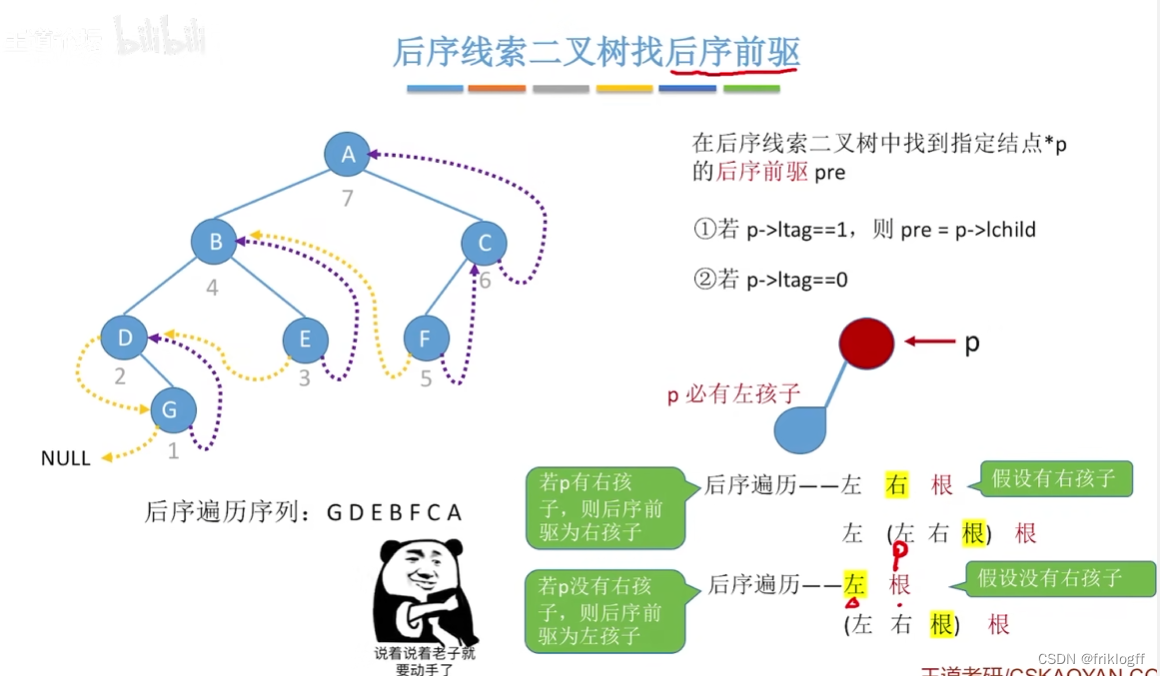
在这里插入图片描述

先序线索二叉树找中序前驱

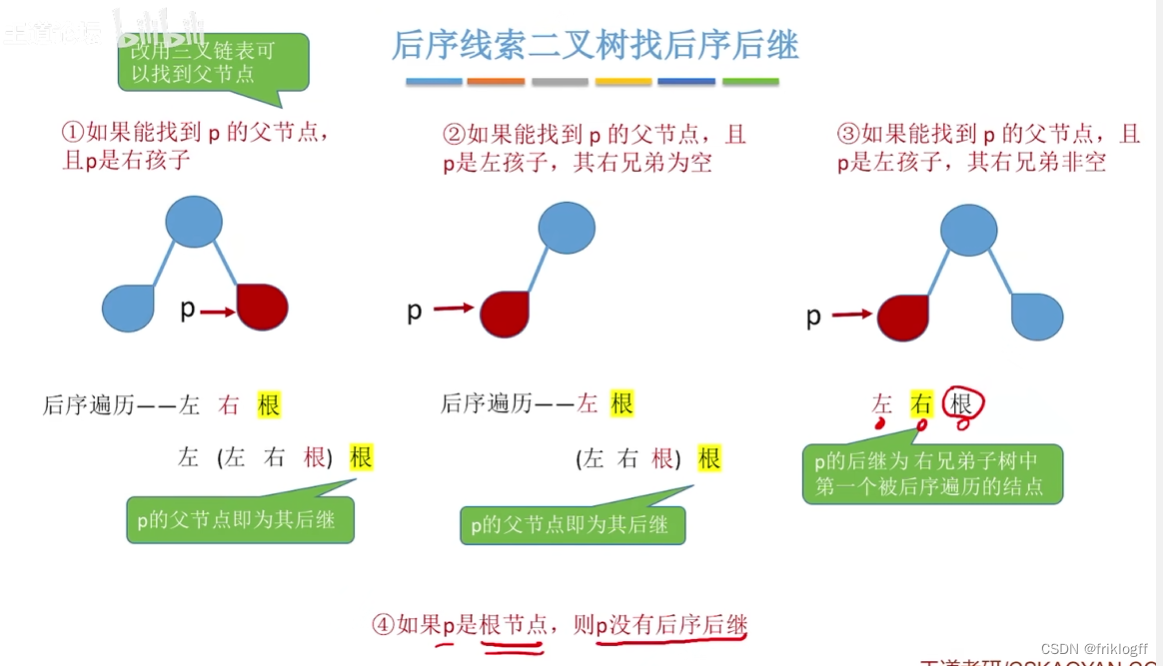
在这里插入图片描述

后序线索二叉树找中序后继

在这里插入图片描述

后序线索二叉树找中序前驱

在这里插入图片描述

小结

在这里插入图片描述

树和森林

树的逻辑结构

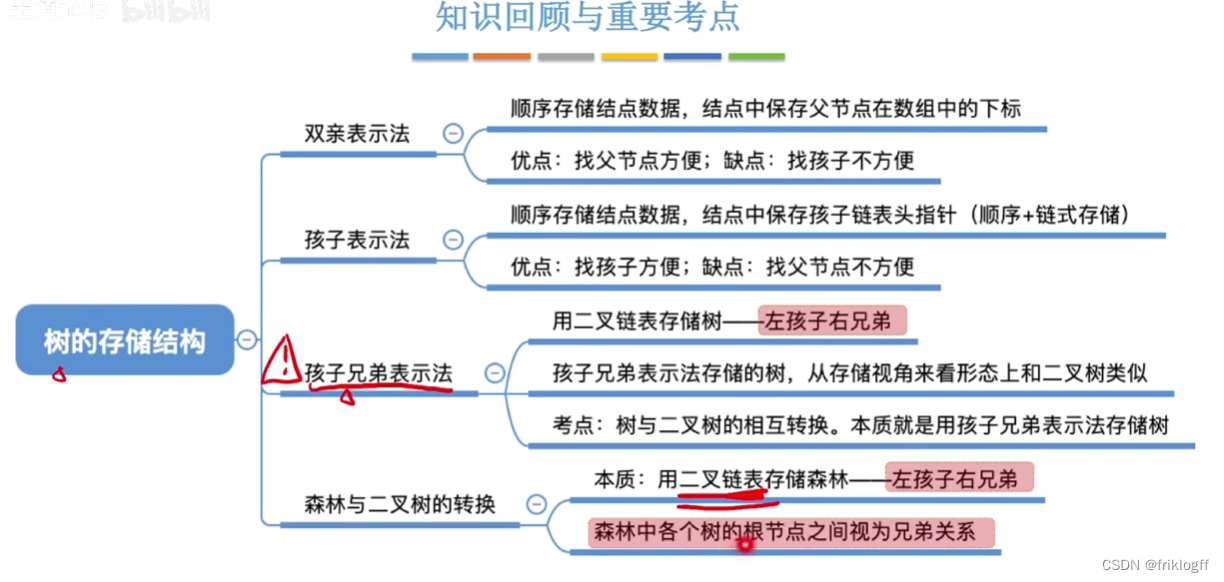
在这里插入图片描述

树的存储结构

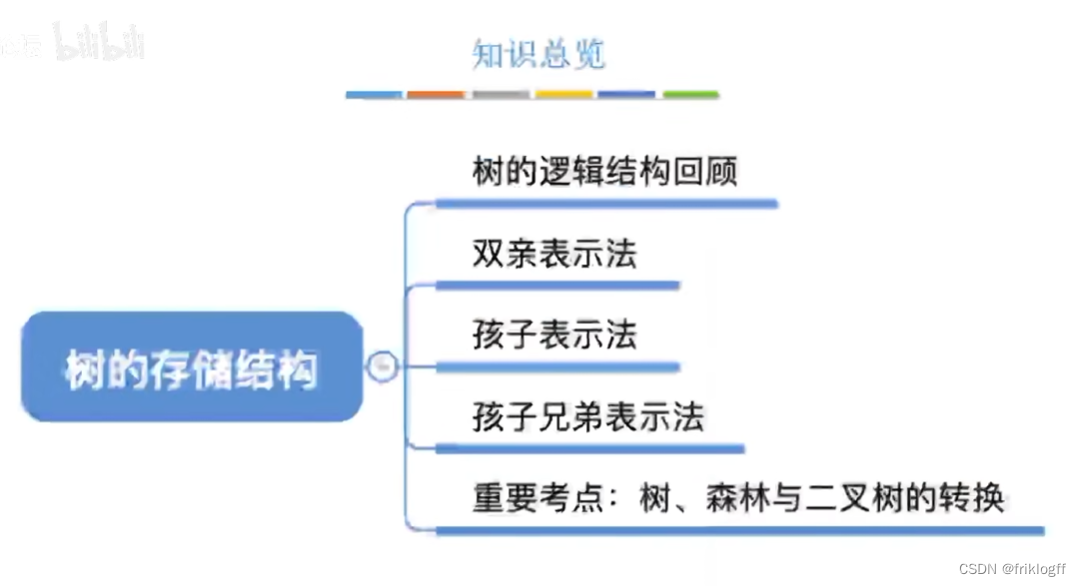
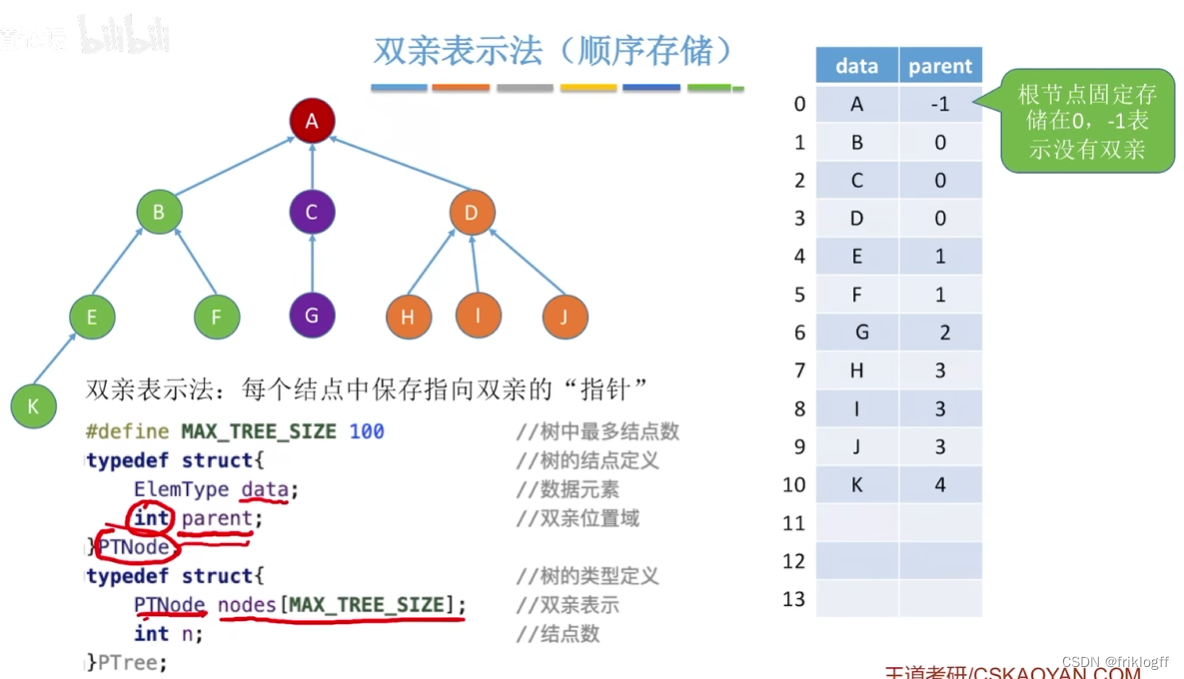
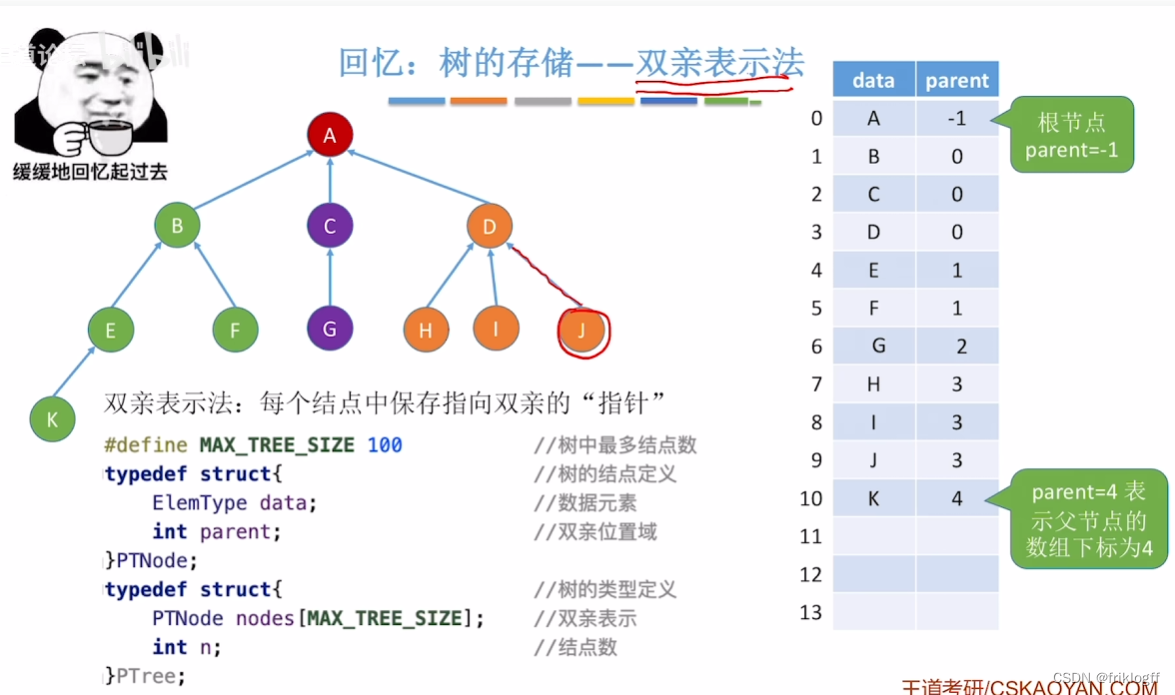
在这里插入图片描述

双亲表示法
- - 概念
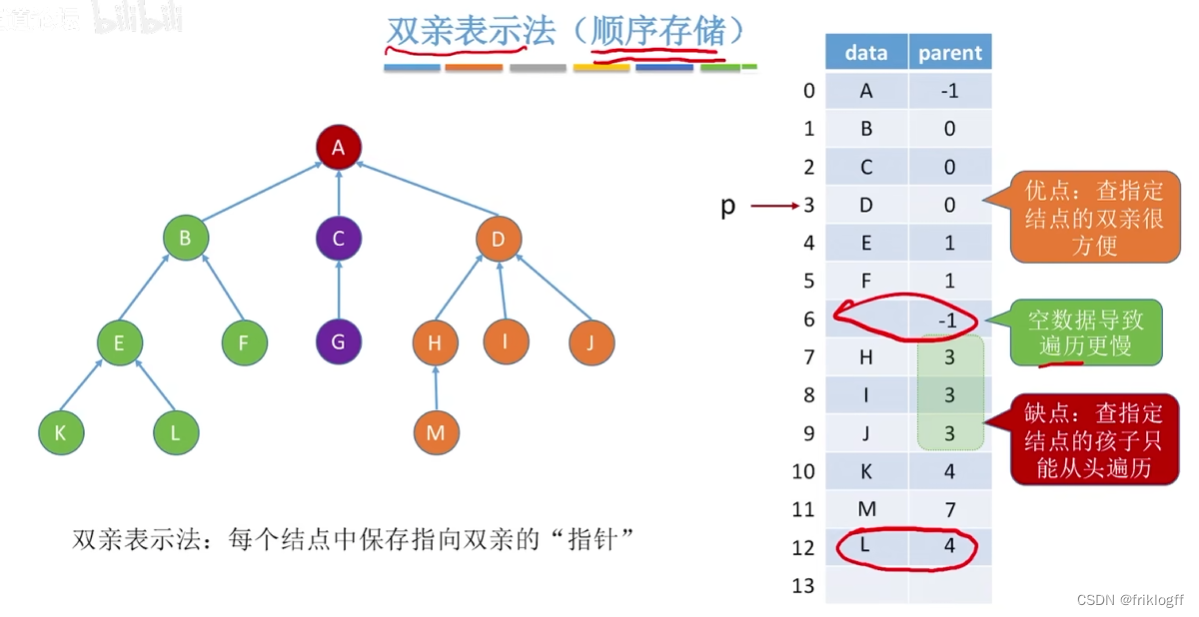
    - 采用一组连续空间来存储每个结点，同时每个结点设一个伪指针，指向双亲在数组的位置
  - 优点
    - 访问结点的双亲快
  - 缺点
    - 访问结点的孩子需要遍历整个结构

在这里插入图片描述

孩子表示法
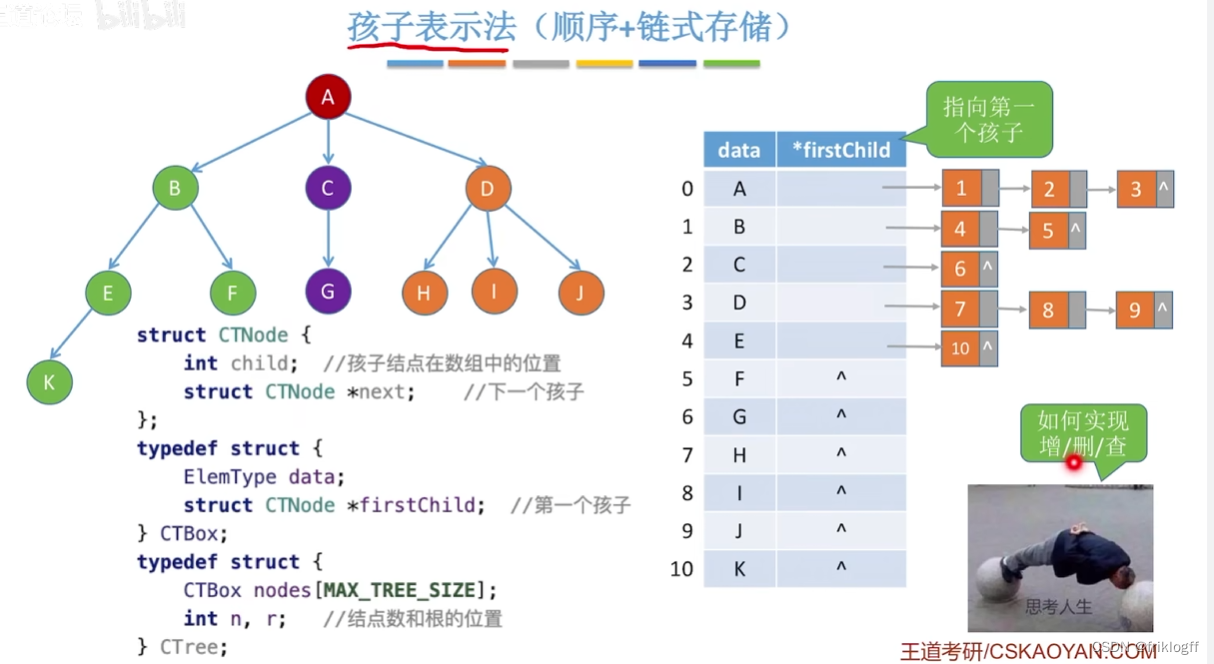
- - 概念
    - 将每个结点的孩子都用单链表链接为一个线性结构
  - 优点
    - 访问孩子结点快
  - 缺点
    - 寻找双亲需要遍历n个结点中孩子链表指针域所指n个孩子链表（可为每个结点设parent域指向父结点）
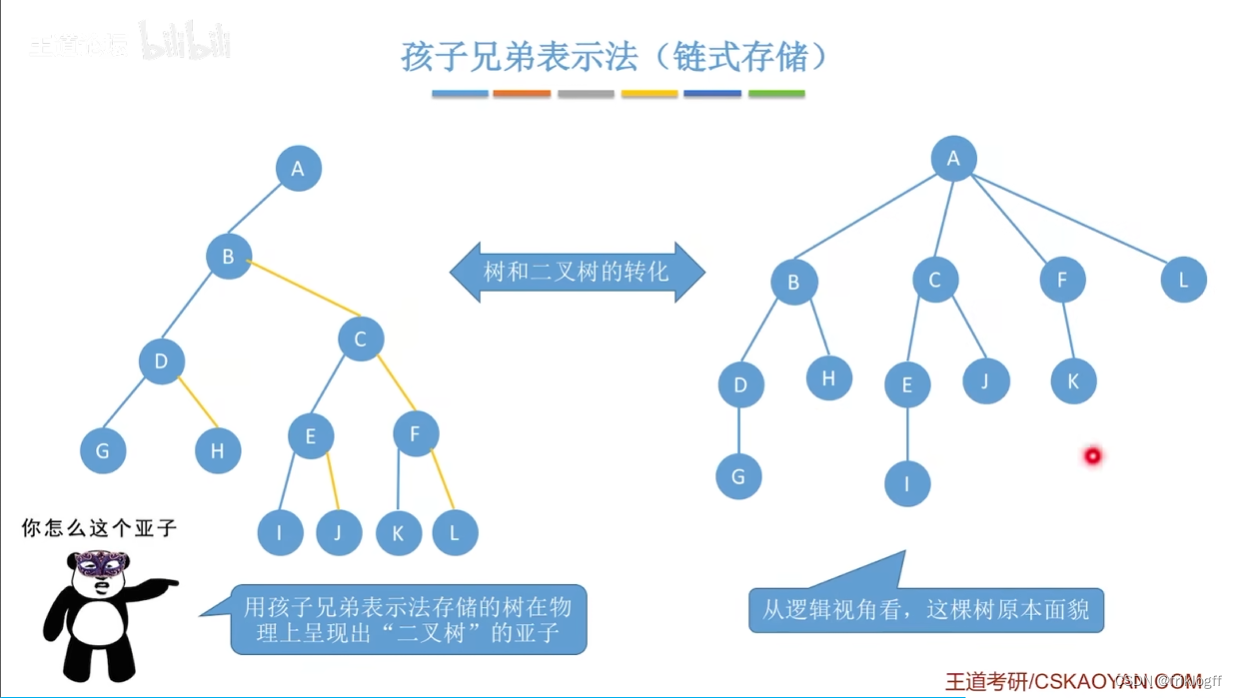
孩子兄弟表示法
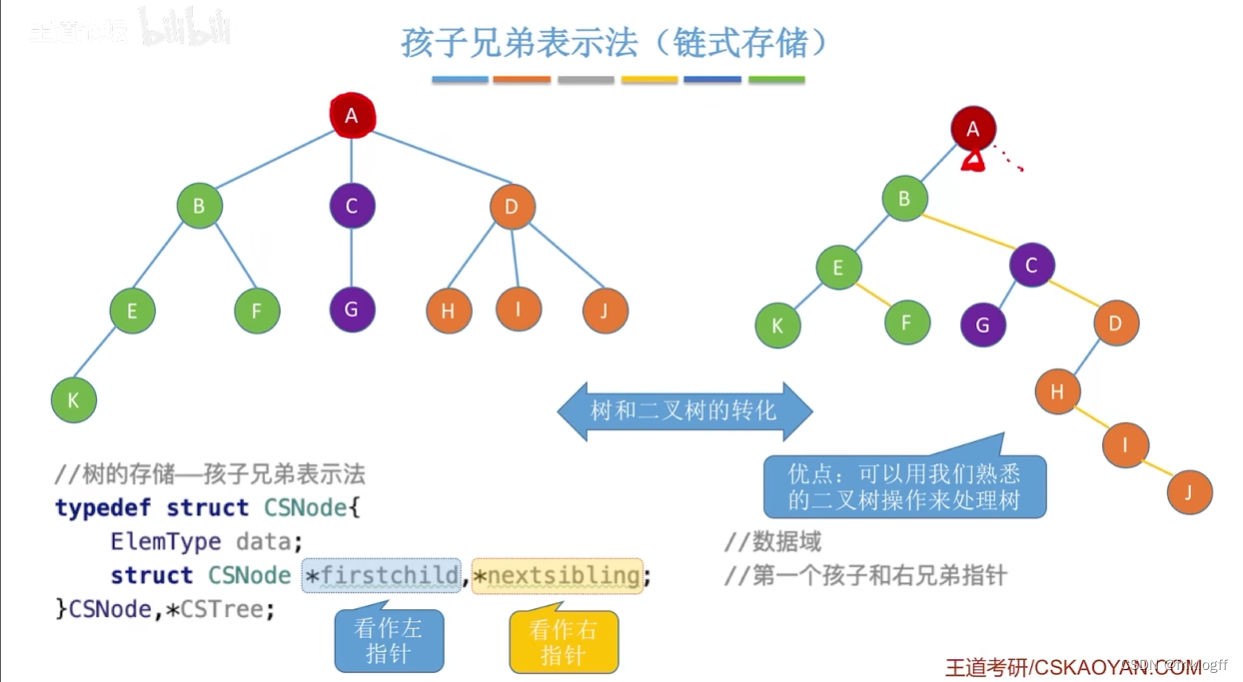
- - 概念
    - 以二叉链表为存储结构，孩子兄弟表示法使每个结点包括：结点值、指向结点第一个孩子的左指针、指向结点下一个兄弟结点的右指针
  - 优点
    - 方便地实现树转换为二叉树的操作，易于查找结点的孩子
  - 缺点
    - 找双亲麻烦（可为每个结点设parent域指向父结点）

树、森林与二叉树的转换

树转换成二叉树
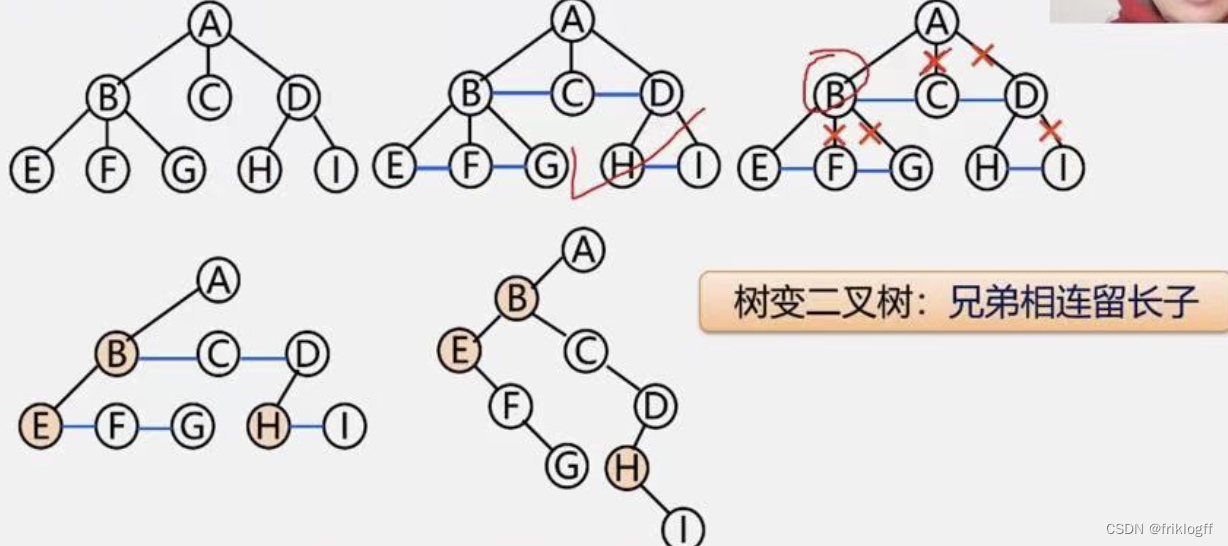
- - 加线：在兄弟之间架一条线
  - 抹线：对每个结点，除了左孩子外，去除其与其余孩子之间的关系
  - 旋转：以树的根结点为轴心，将树顺时针旋转45度
二叉树转换成树
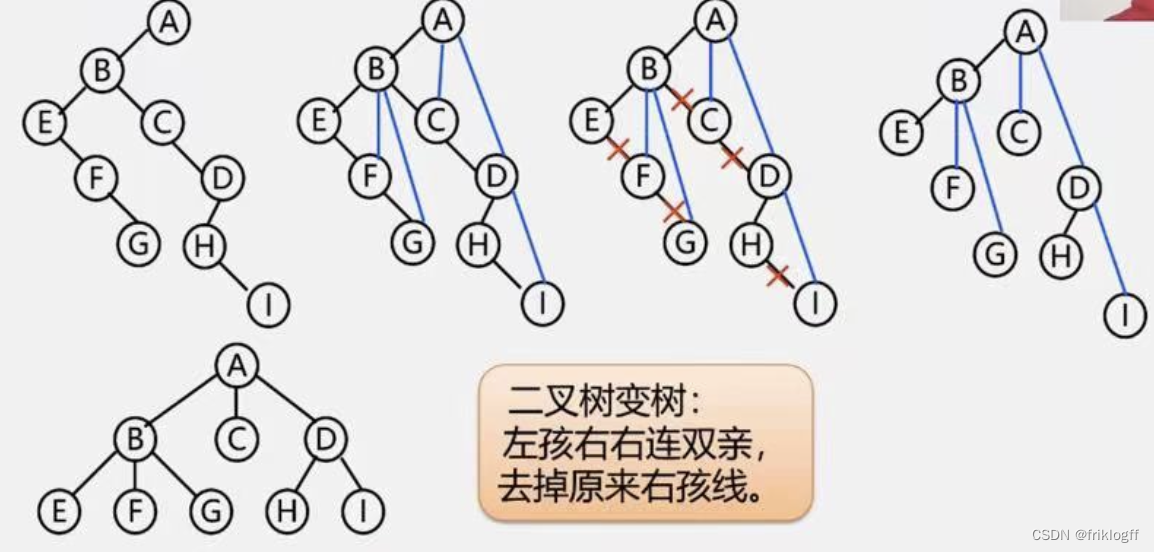
- - 加线：若p结点是双亲结点的左孩子，则将p的右孩子，右孩子的右孩子…沿分支找到的所有右孩子，都与p的双亲连起来
  - 抹线：抹掉原二叉树中双亲与右孩子之间的连线
  - 调整：将结点按层次排序，形成树结构
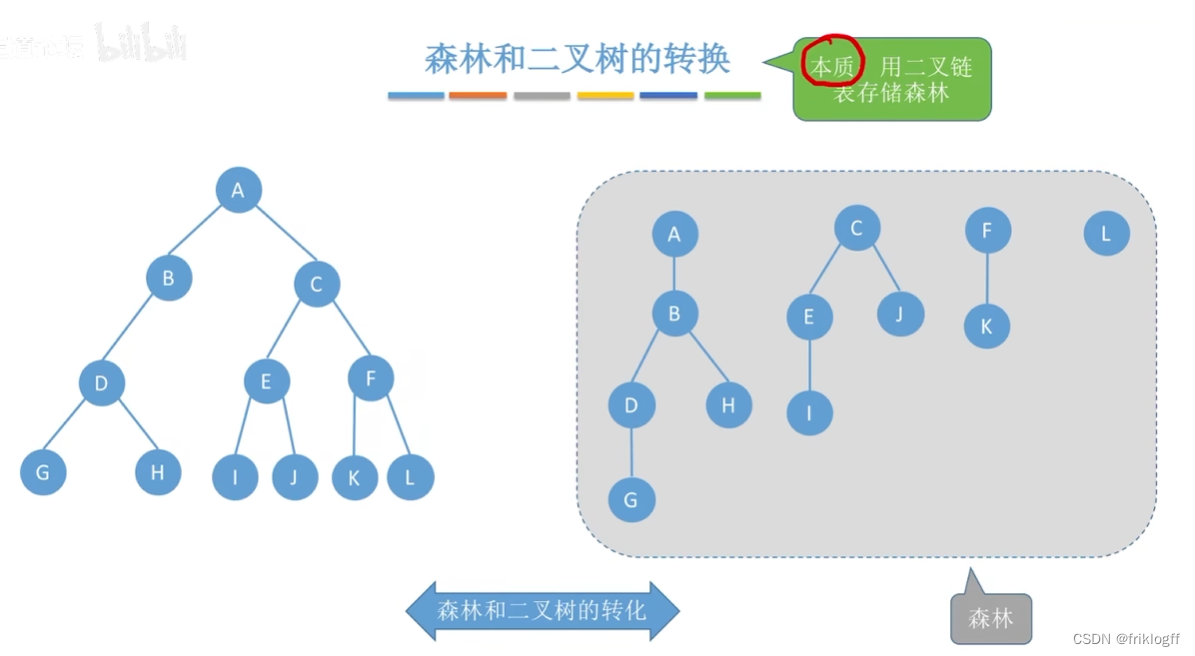
森林转换成二叉树
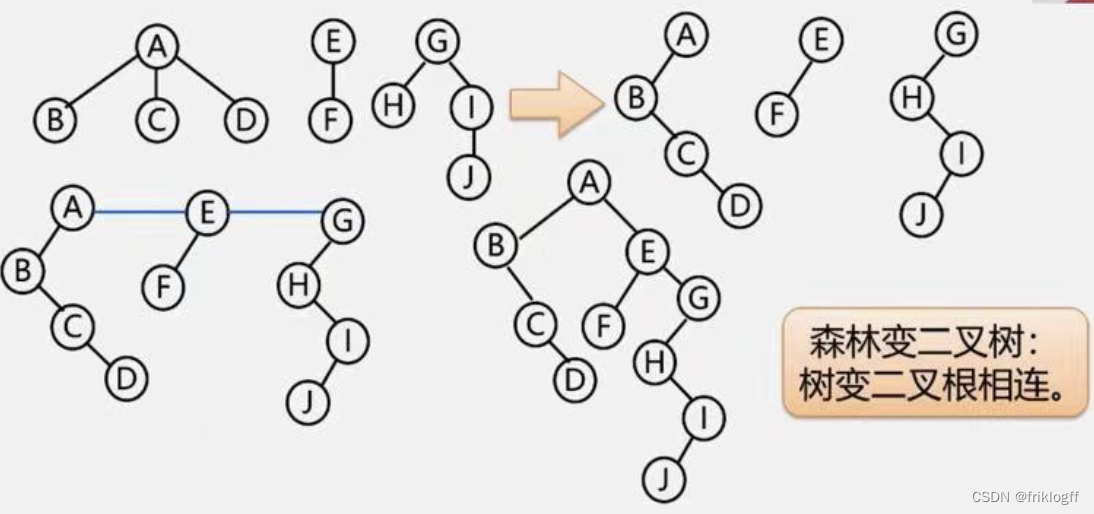
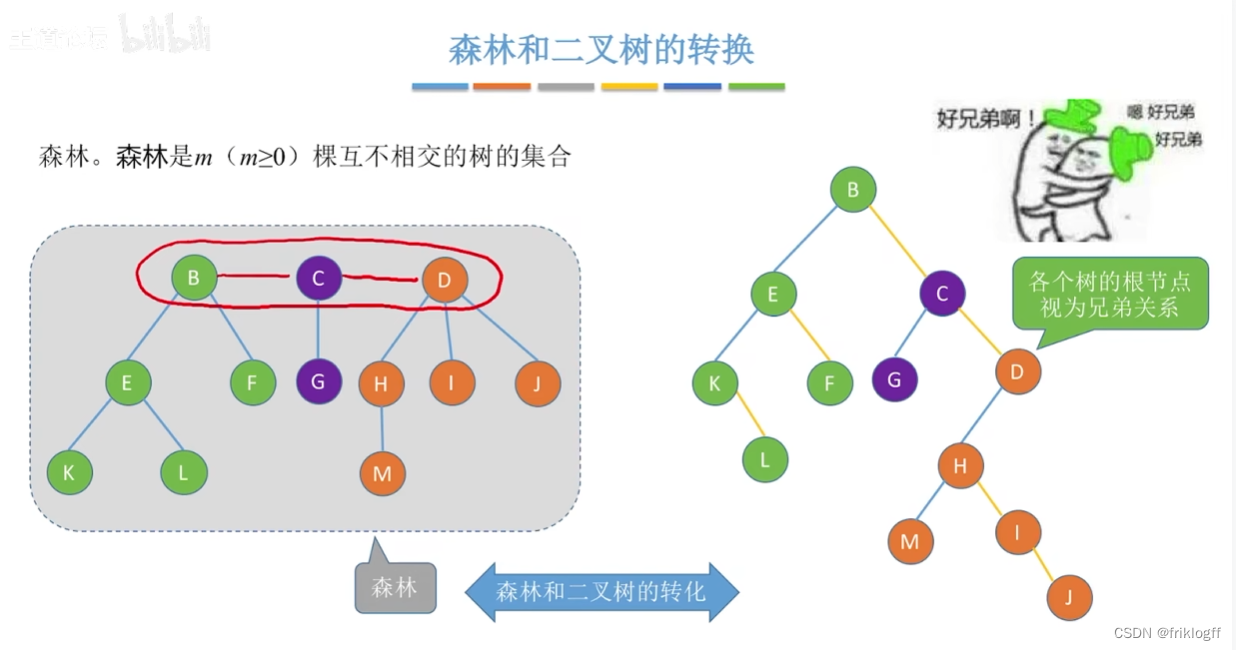
- - 将个棵树分别转换成二叉树
  - 将每棵树的根结点用线相连
  - 以第一课树根结点为二叉树的根，顺时针旋转即可
二叉树转换成森林
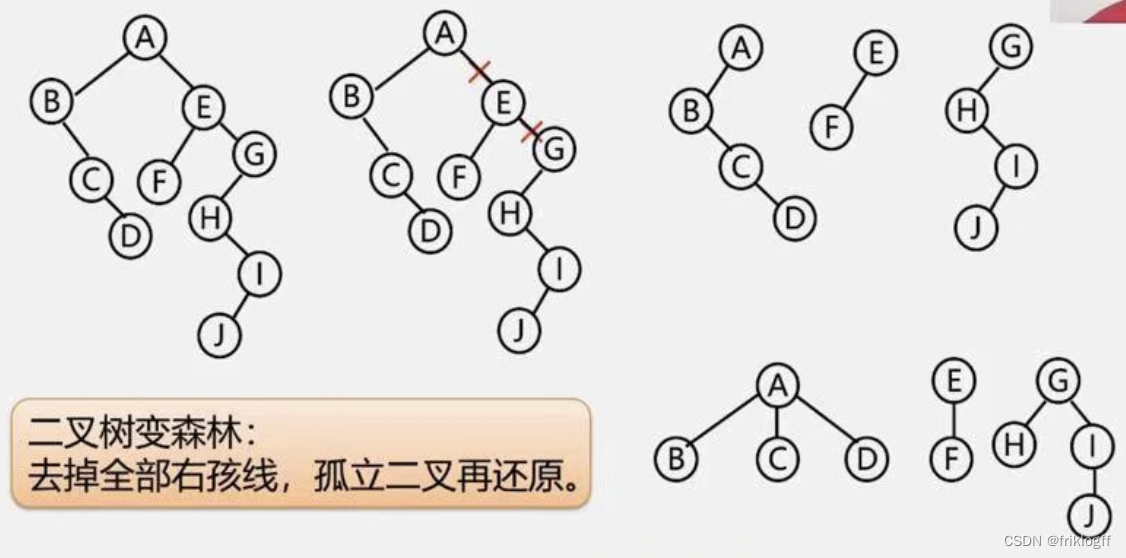
- - 抹线：将二叉树中根结点与其右孩子连线，及沿右分支搜索到的所有右孩子间连线全部抹掉
  - 还原：将孤立的二叉树还原成树

在这里插入图片描述

树和森林的遍历

树
- 深度优先遍历
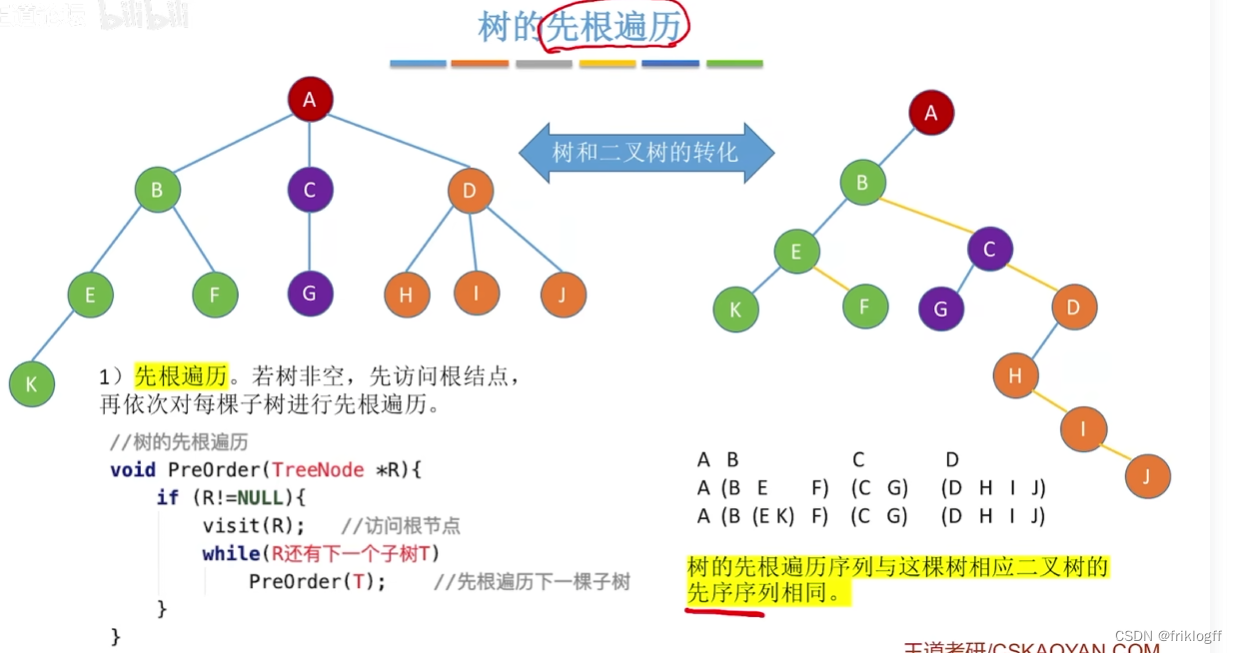
  - 先根遍历
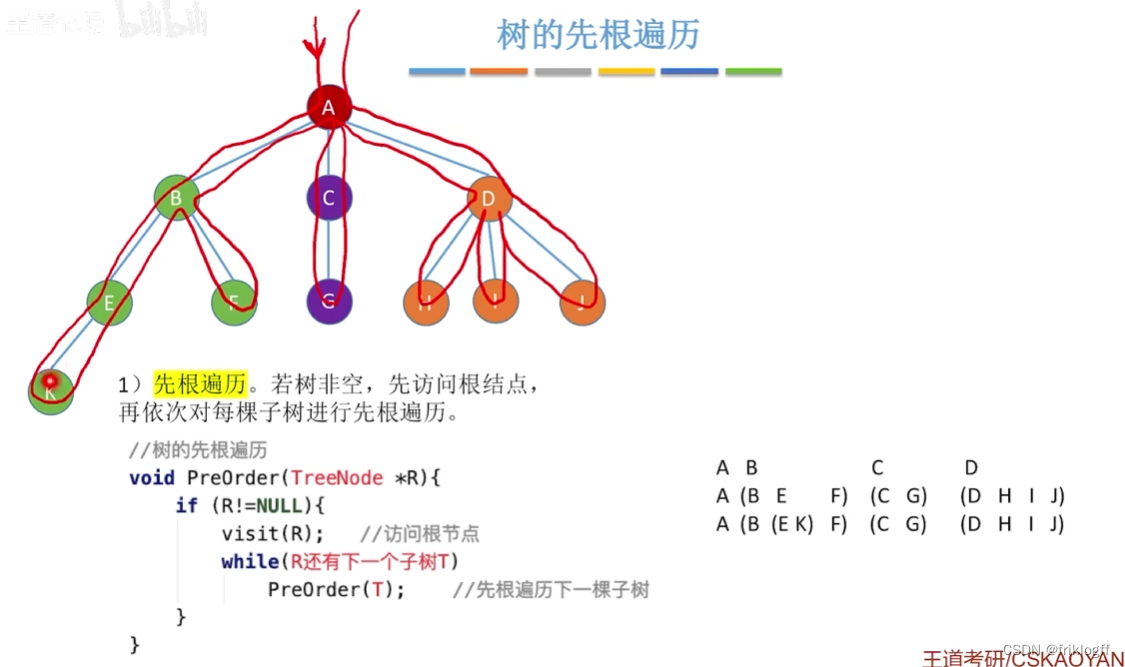
    - 若树非空，先访问根结点，再用先根遍历规则依次遍历根结点的每一颗子树
    - 其遍历序列与这棵树相应二叉树的先序序列相同
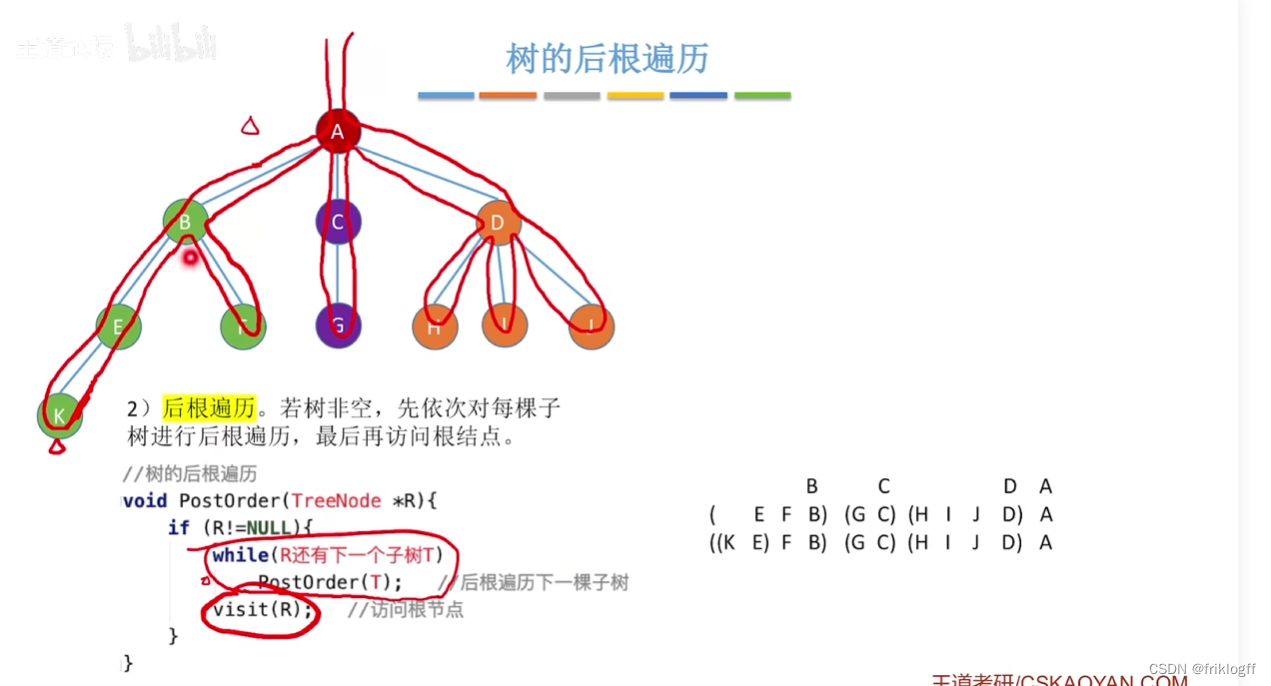
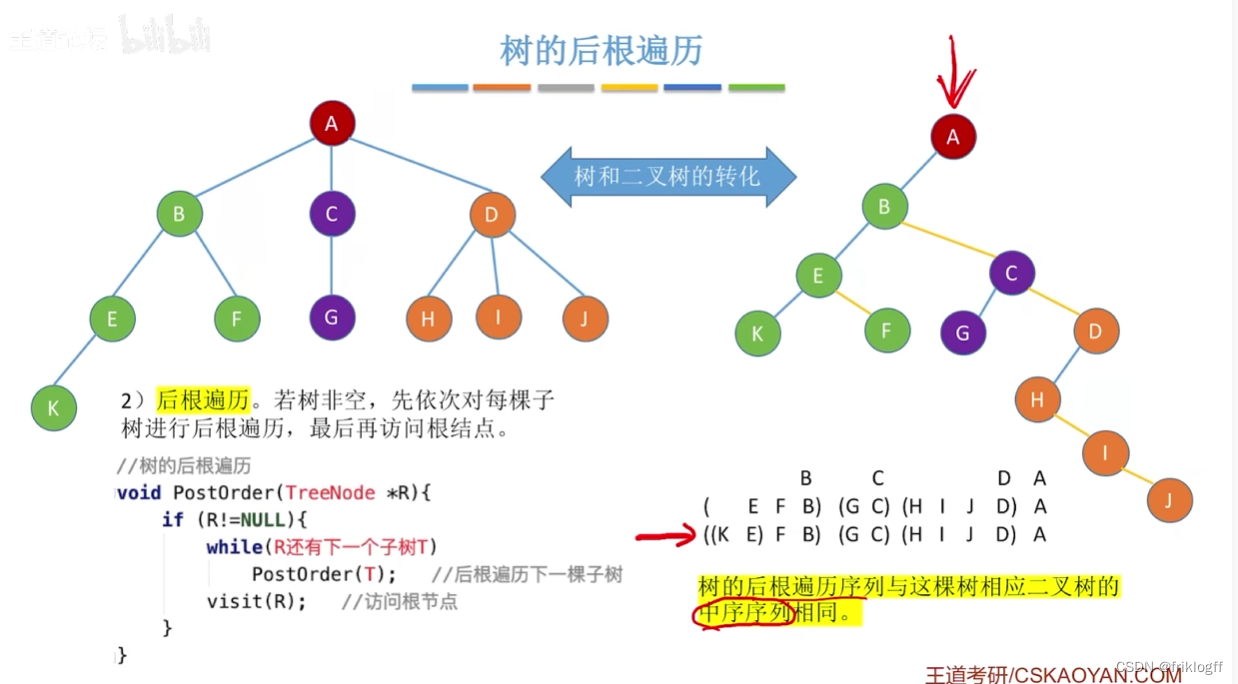
  - 后根遍历
  - 若树非空，先用后根遍历规则依次遍历根结点的每一颗子树，再访问根结点
  - 其遍历序列与这棵树相应二叉树的中序序列相同
- 广度优先遍历
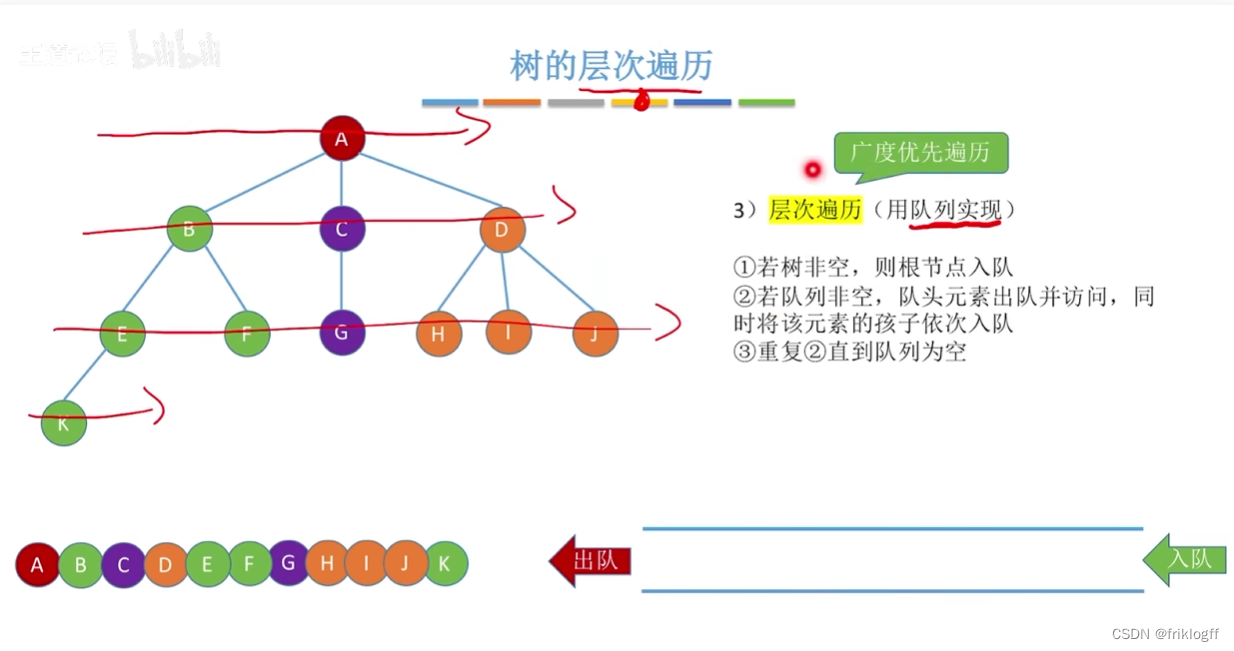
森林
- 先序遍历
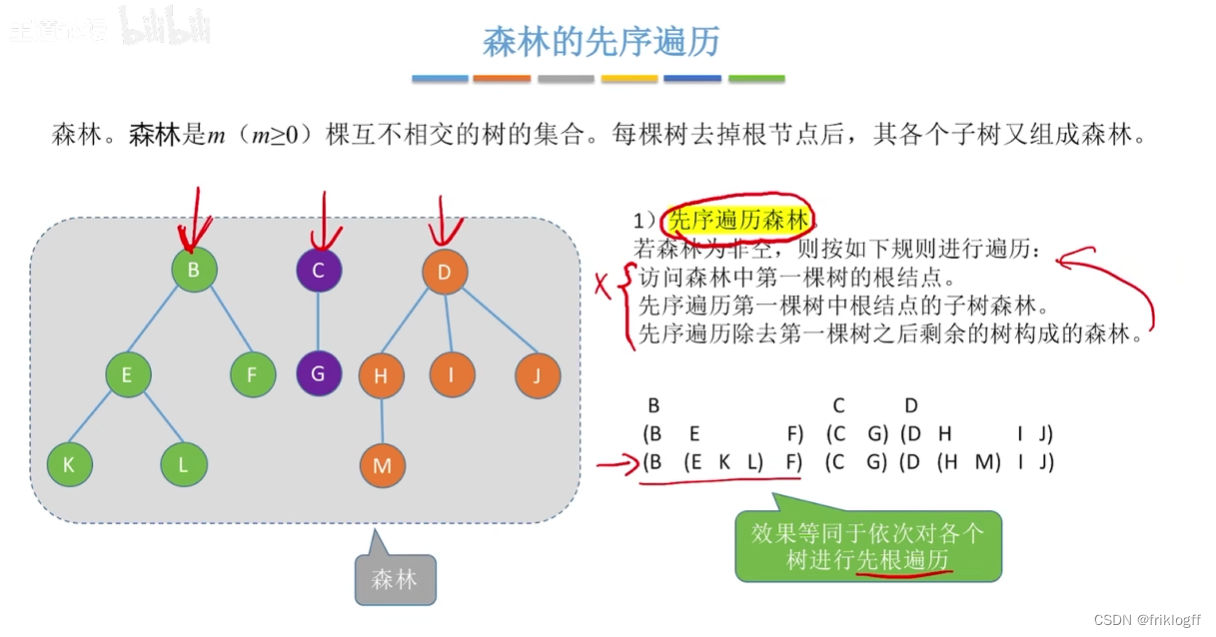
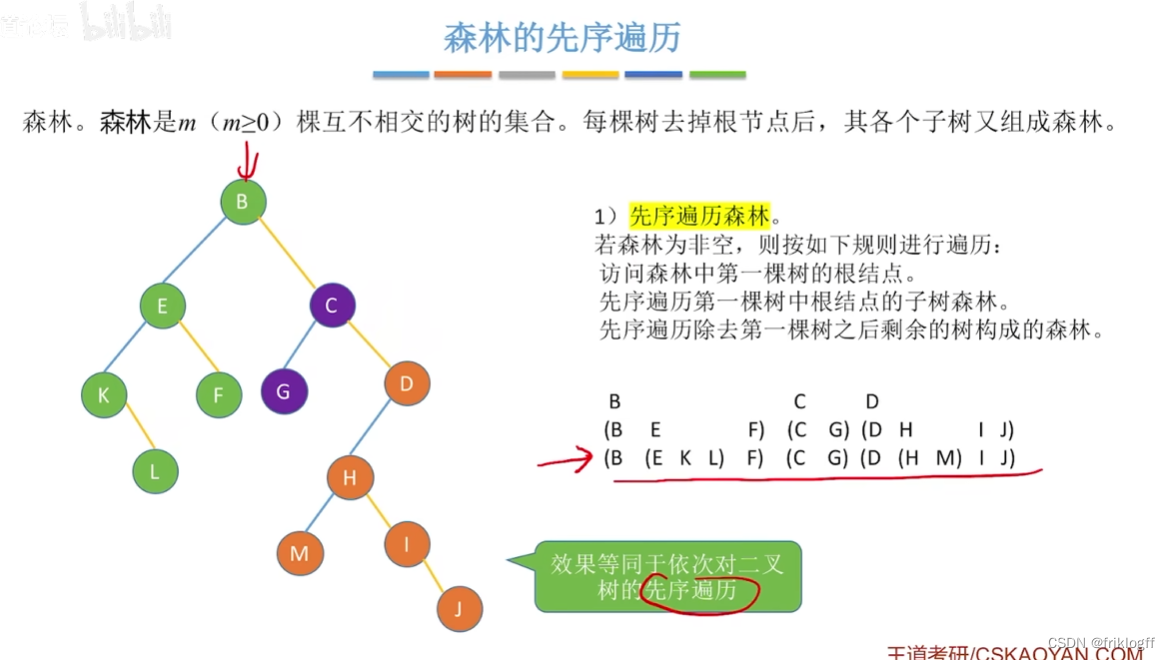
  - 访问森林中第一棵树的根结点
  - 先序遍历第一棵树中根结点的子树森林
  - 先序遍历除去第一棵树之后剩余树构成的森林
- 中序遍历
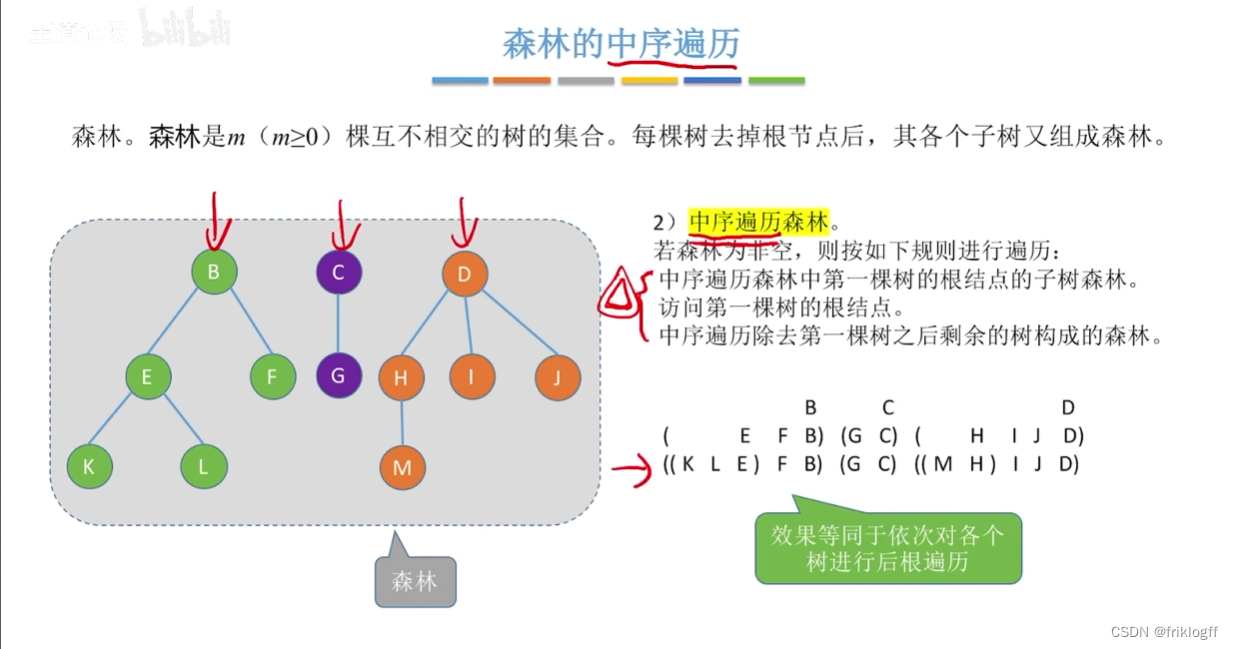
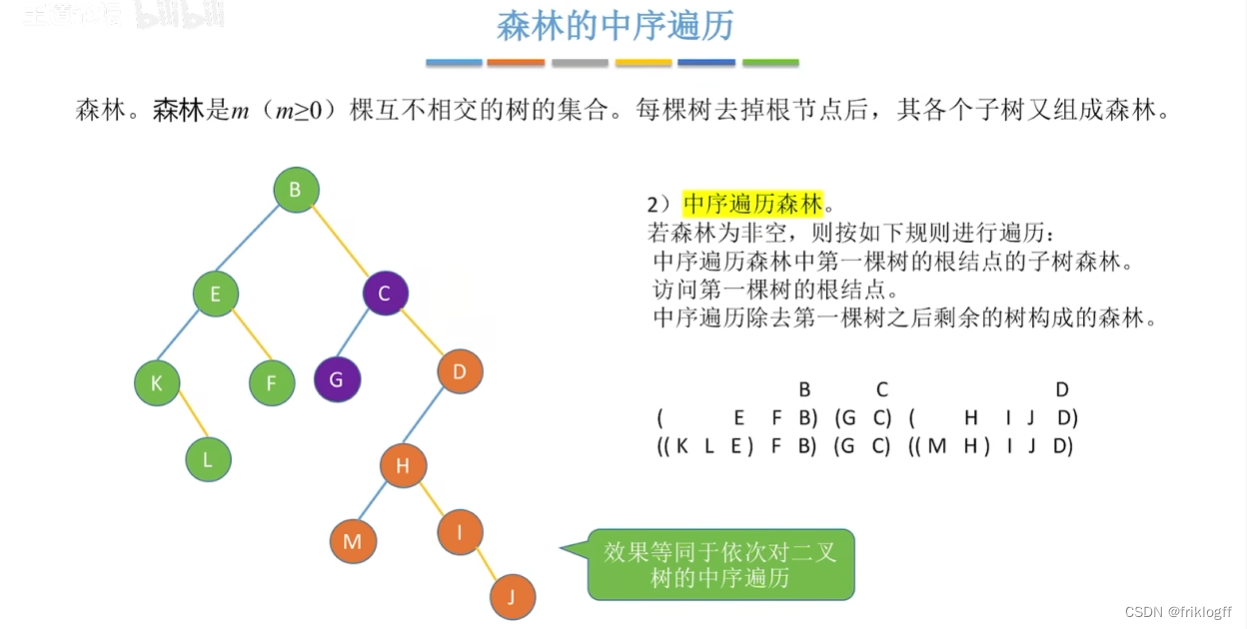
  - 中序遍历森林中第一棵树的根结点的子树森林
  - 访问第一棵树的根结点
  - 中序遍历除去第一棵树之后剩余树构成的森林
对应关系

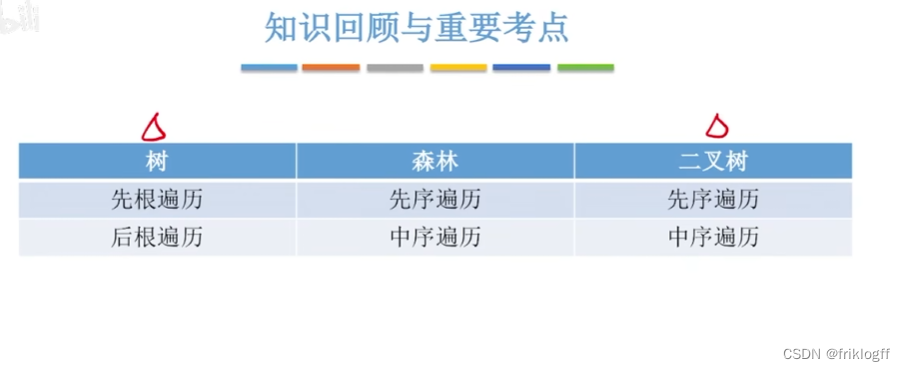
哈夫曼树及其应用

基本概念

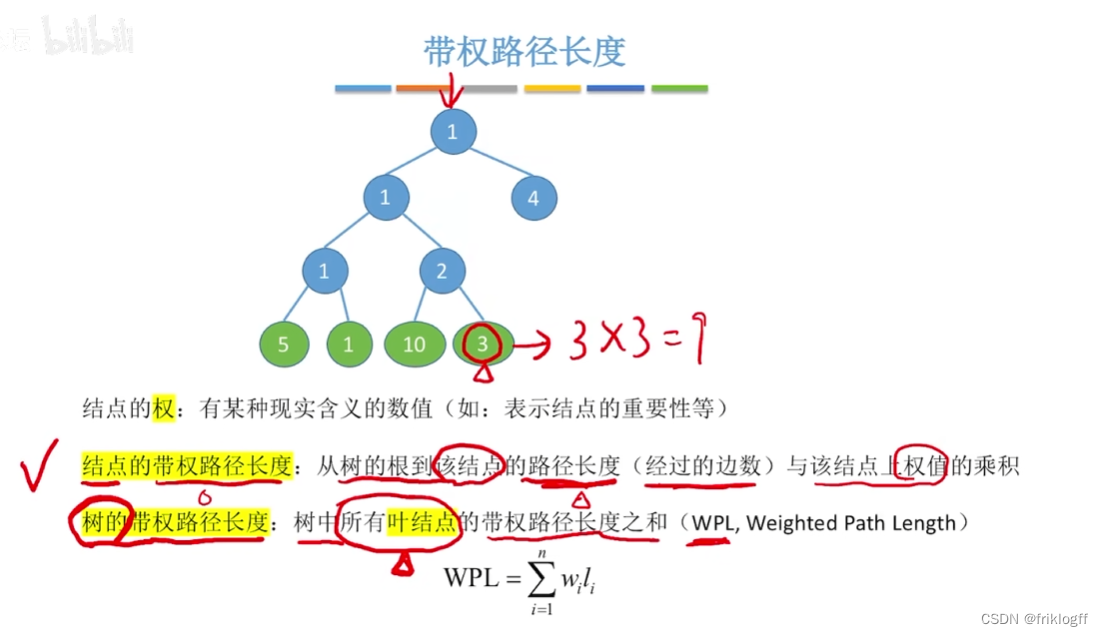
在这里插入图片描述

路径
- 从树中一个结点到另一个结点之间的分支构成这两个结点间的路径
结点的路径长度
- 两结点间路径上的分支数
树的路径长度
- 从树根到每个结点的路径长度之和
权
- 将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权
结点的带权路径长度
- 从根结点到该结点之间的路径长度与该结点的权的乘积
树的带权路径长度
- 树中所有叶子结点的带权路径长度之和

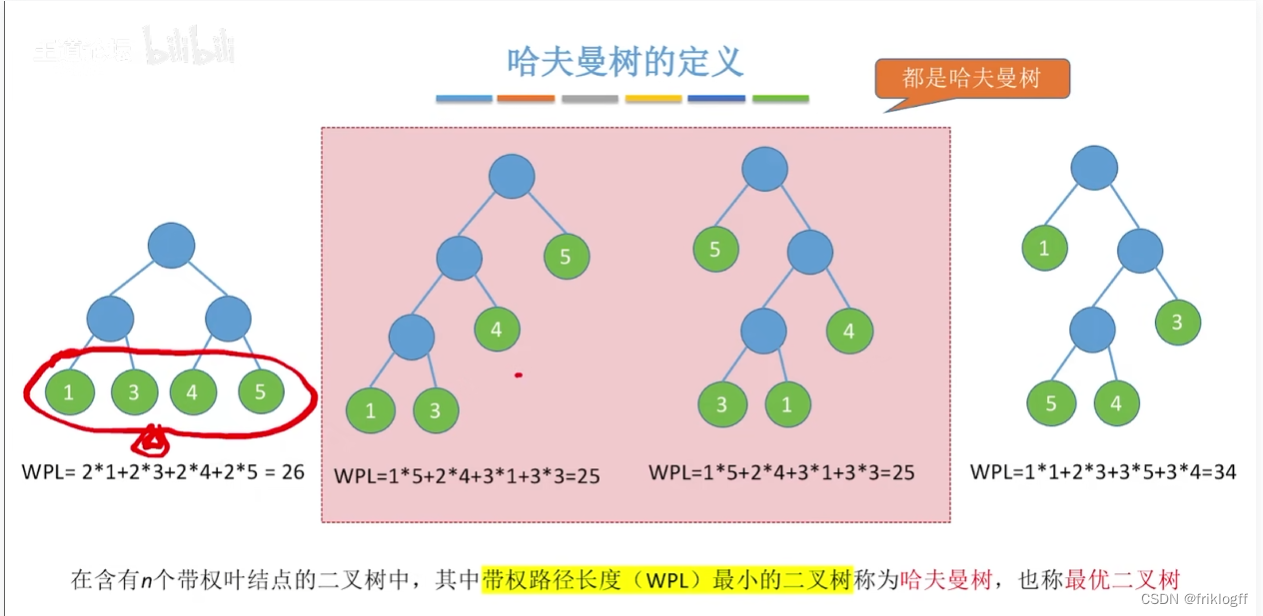
哈夫曼树的定义

最优二叉树，带权路径长度（WPL）最短的二叉树

哈夫曼树的构造

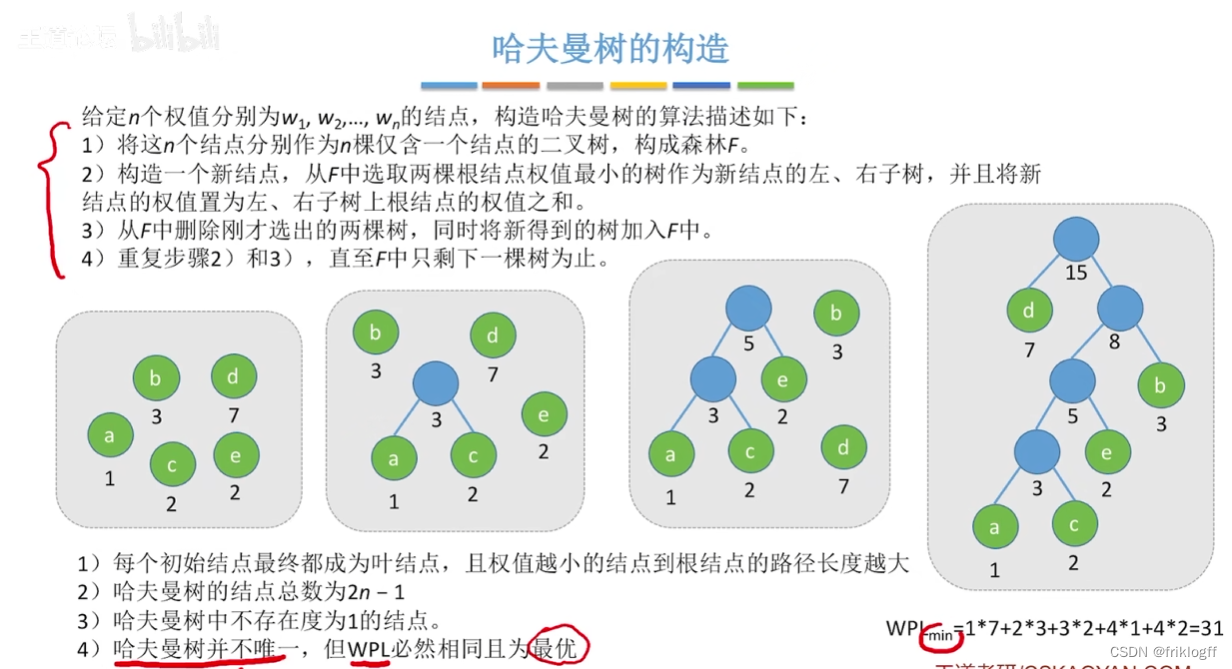
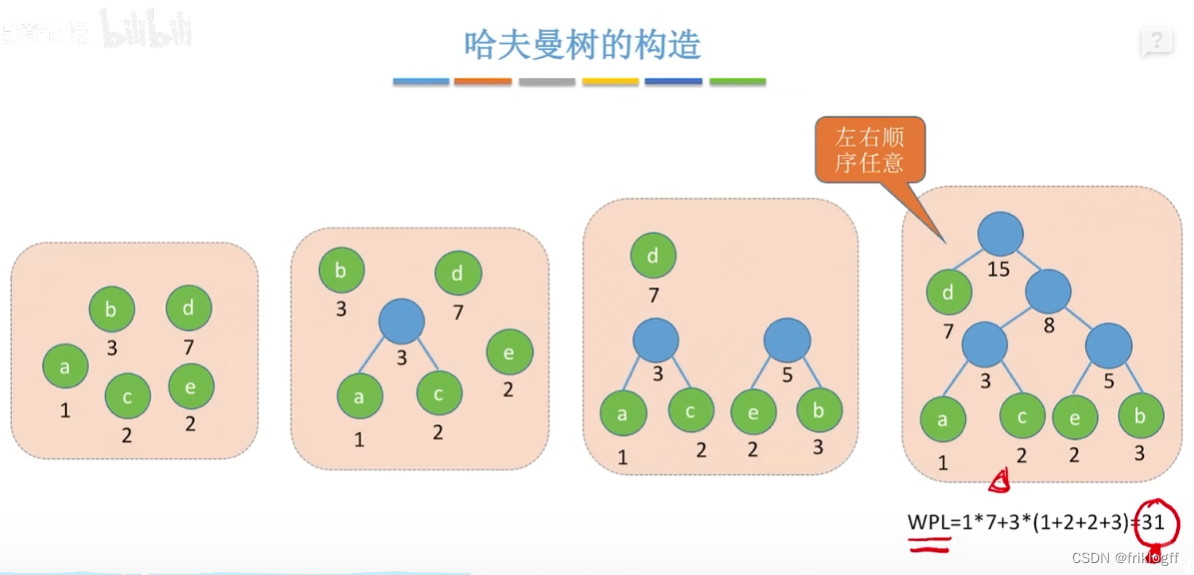
- 每次从合成后存在的结点中选出两个权最小的进行构造二叉树，直到所有结点均在树中

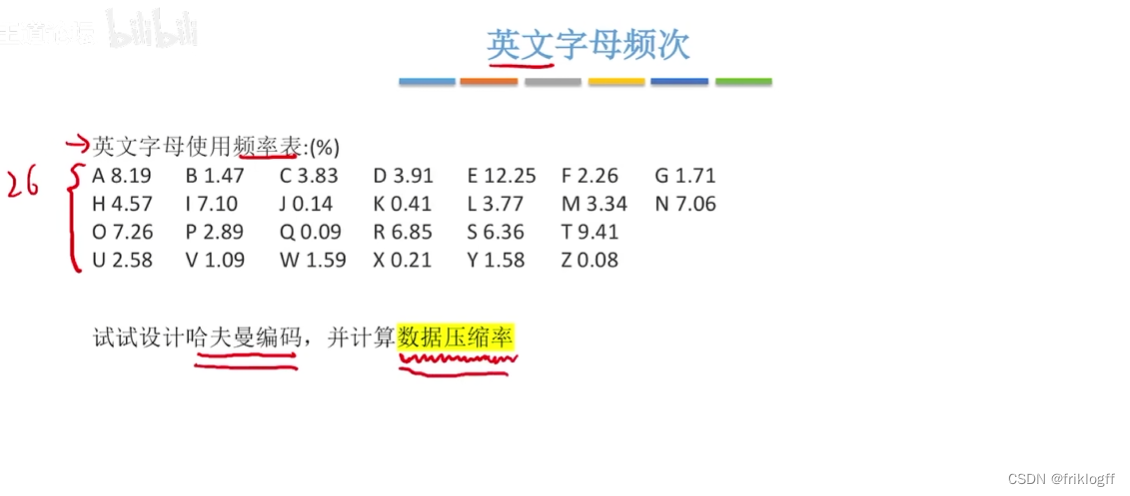
哈夫曼编码

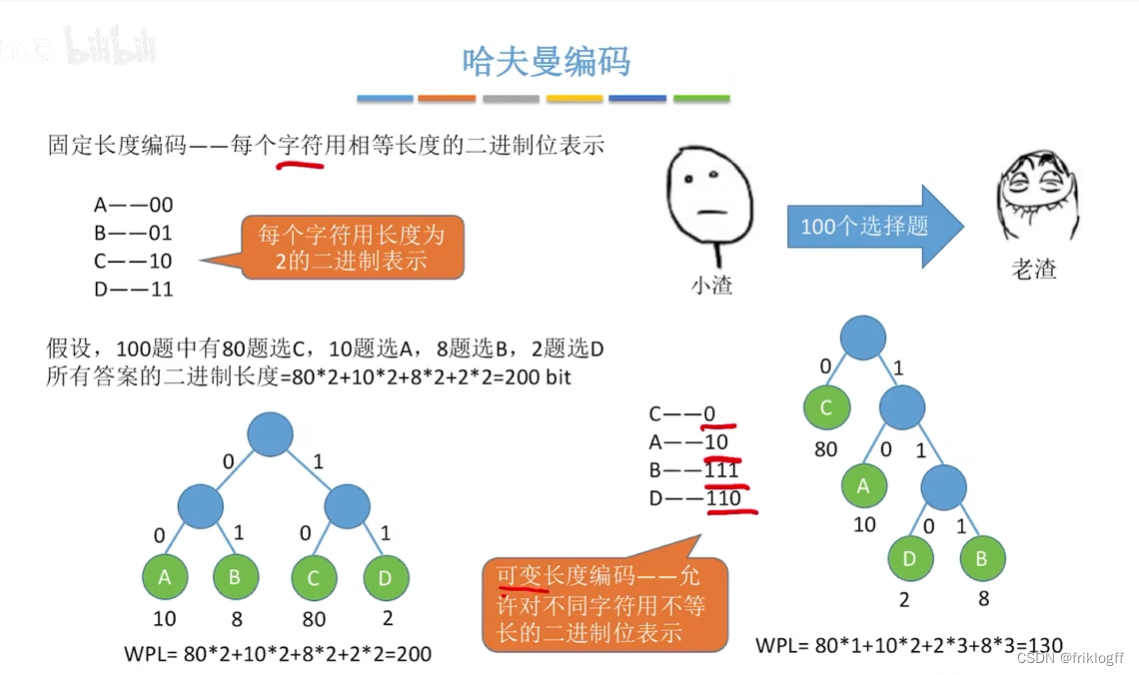
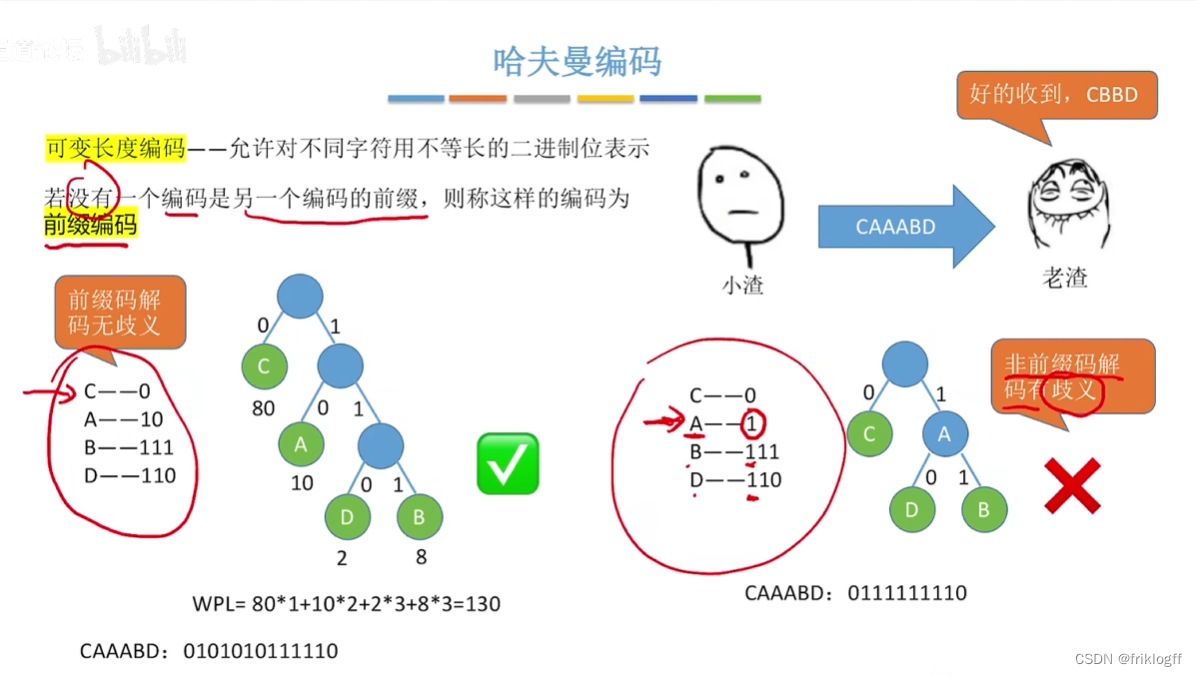
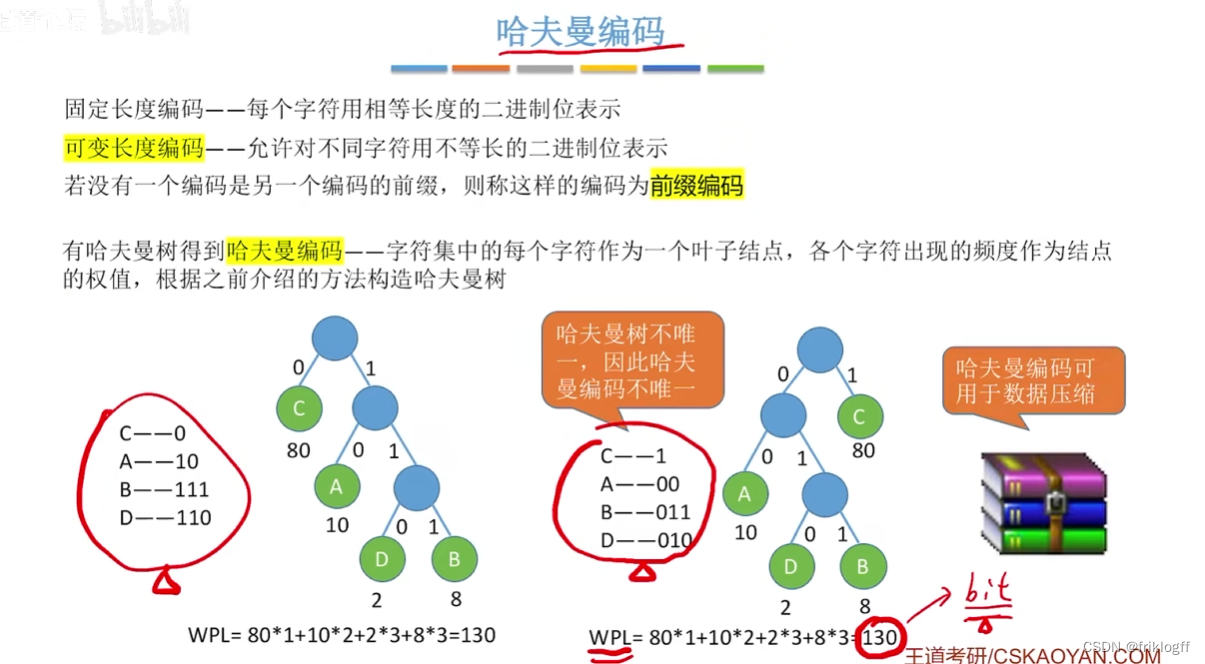
在这里插入图片描述

哈夫曼树的应用，数据压缩编码技术，是最优前缀码
基本概念
- 固定长度编码：在数据通信中，对每个字符用等长二进制位表示
- 可变长编码：对频率高的字符赋以短编码，而对频率较低的字符则赋以较长一些的编码，起到压缩效果
- 前缀编码：没有一个编码是另一个编码的前缀
构造哈夫曼编码
- 将每个出现的字符当作一个独立的结点，其权值为它出现的频度（或次数），构造出对应的哈夫曼树
- 将字符的编码解释为从根至该字符的路径上边标记的序列
- 其中边标记为0表示“转向左孩子”，标记为1表示“转向右孩子”

多叉哈夫曼树（题目考点，类比外部排序的知识点），补0结点（虚叶结点）

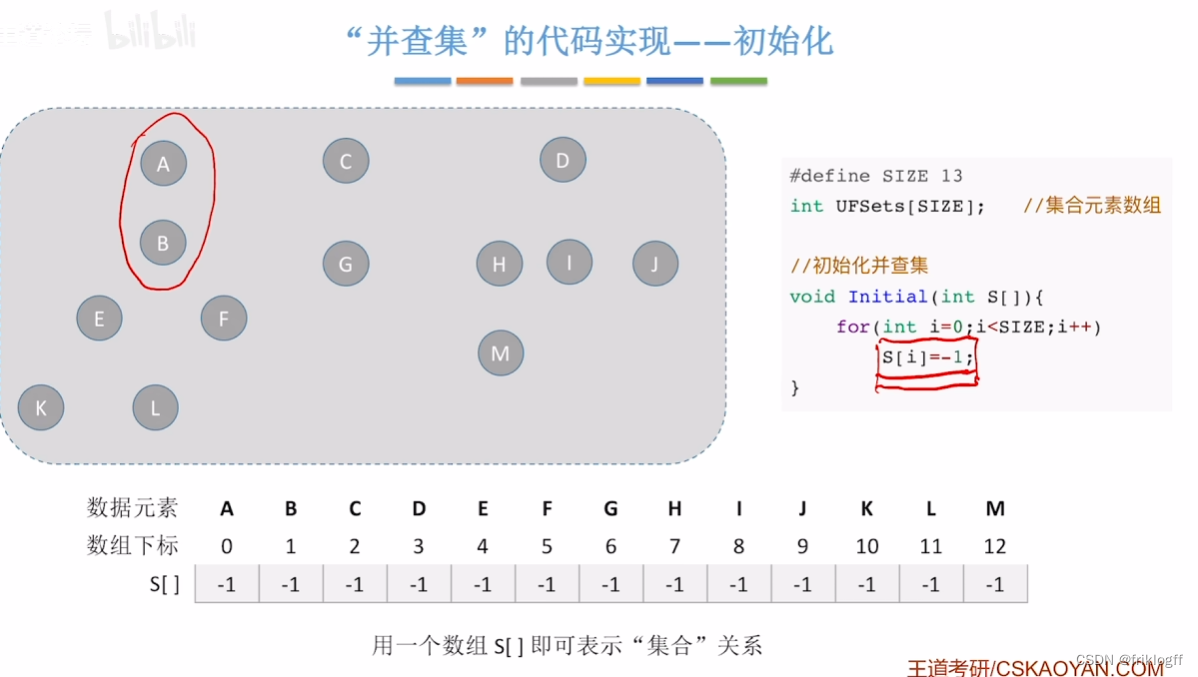
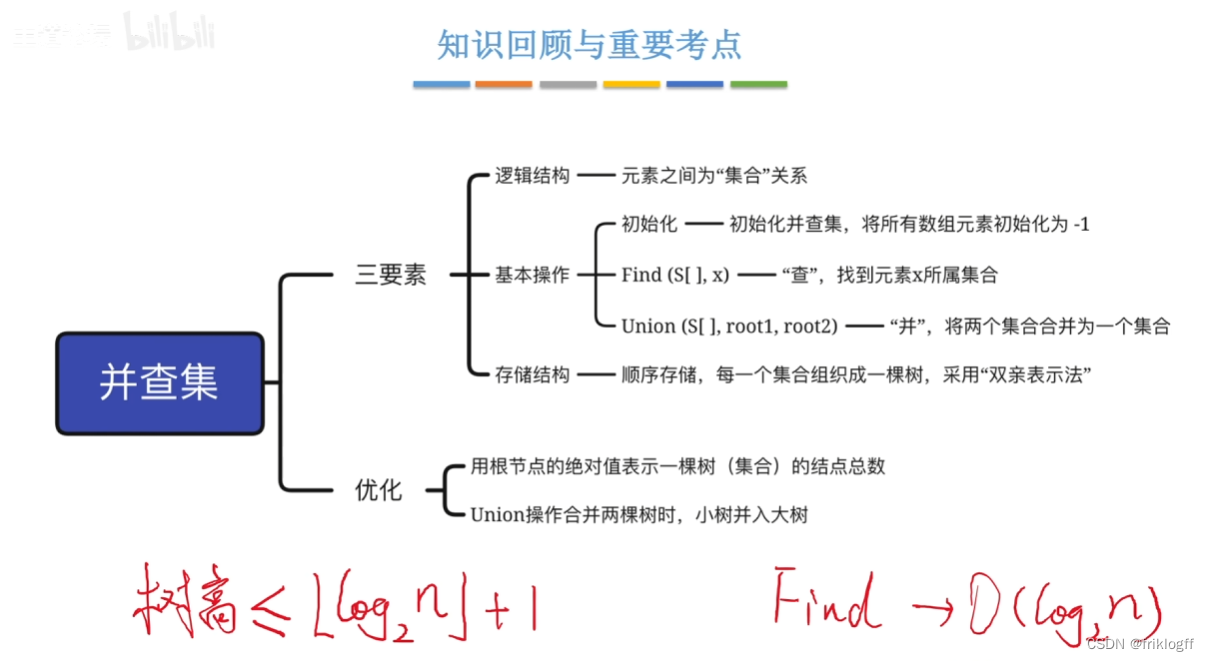
并查集

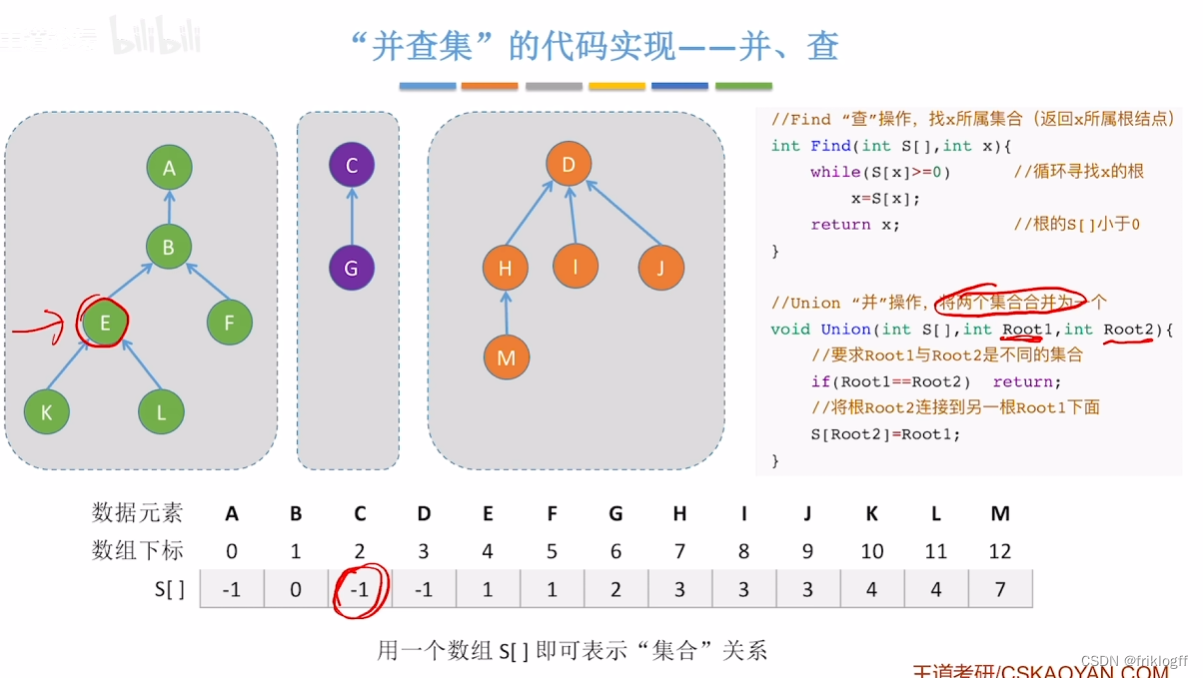
在这里插入图片描述

查

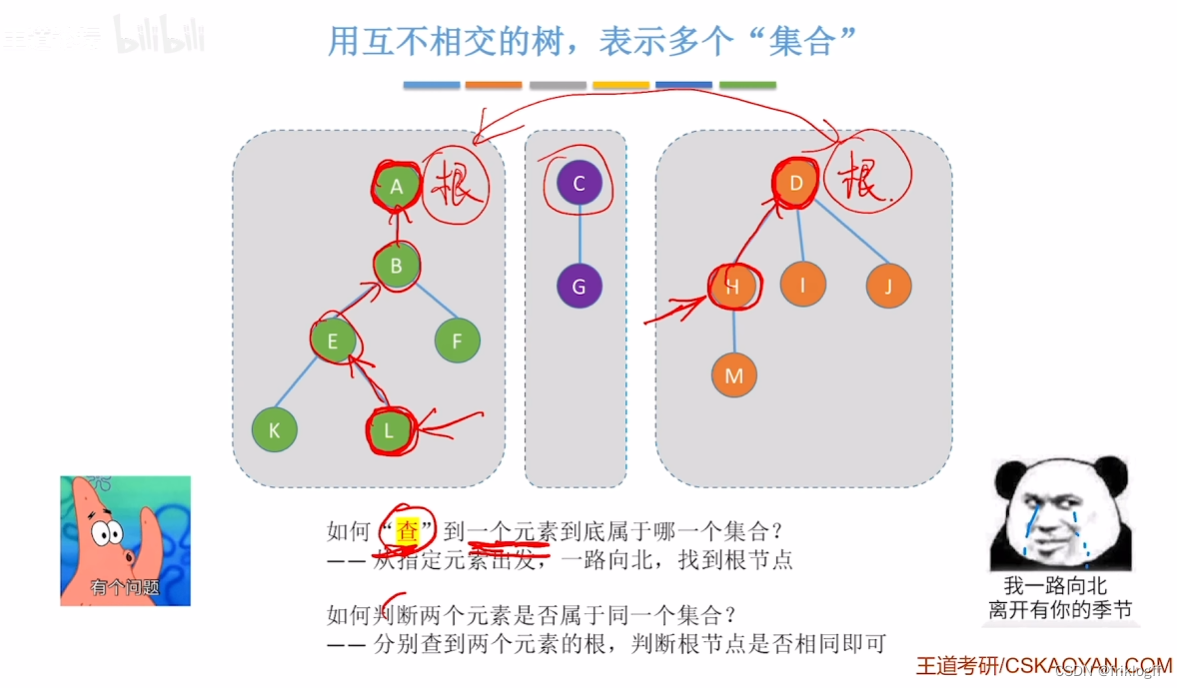
在这里插入图片描述

并

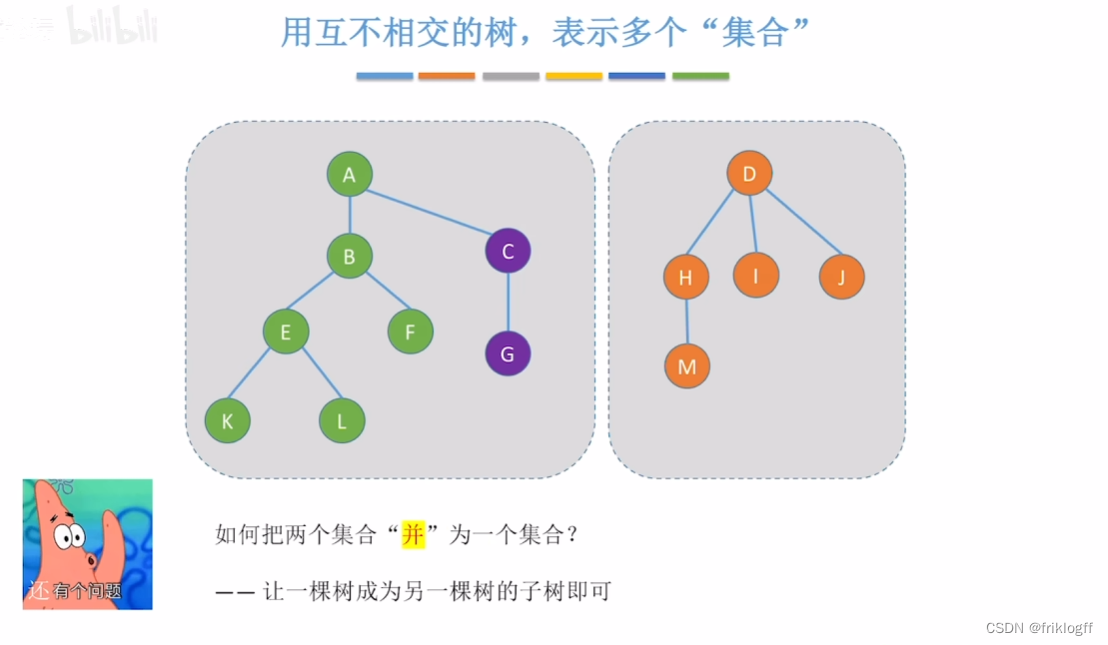
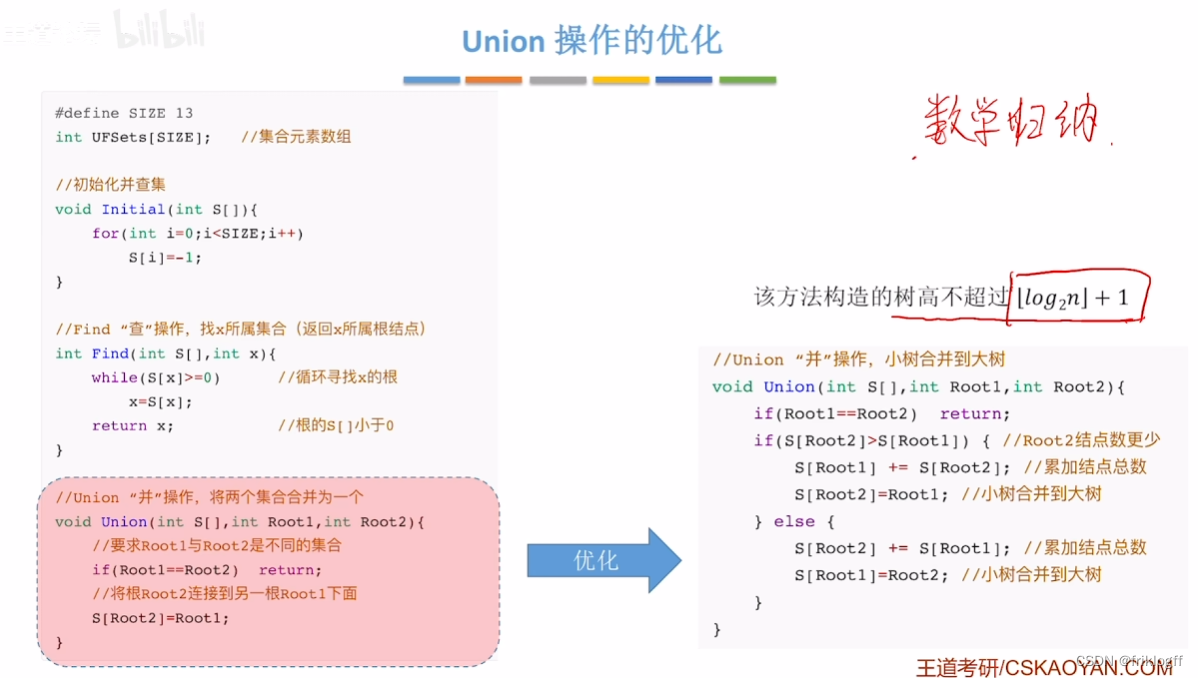
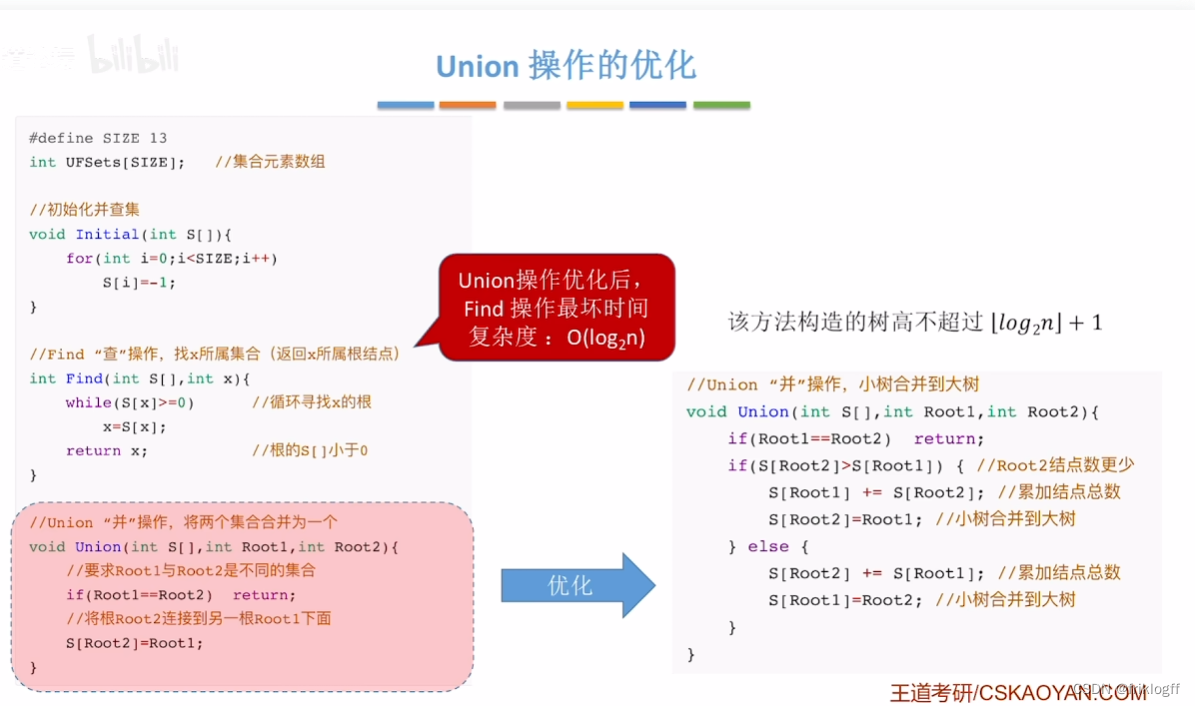
在这里插入图片描述

基本思路

在这里插入图片描述

存储结构
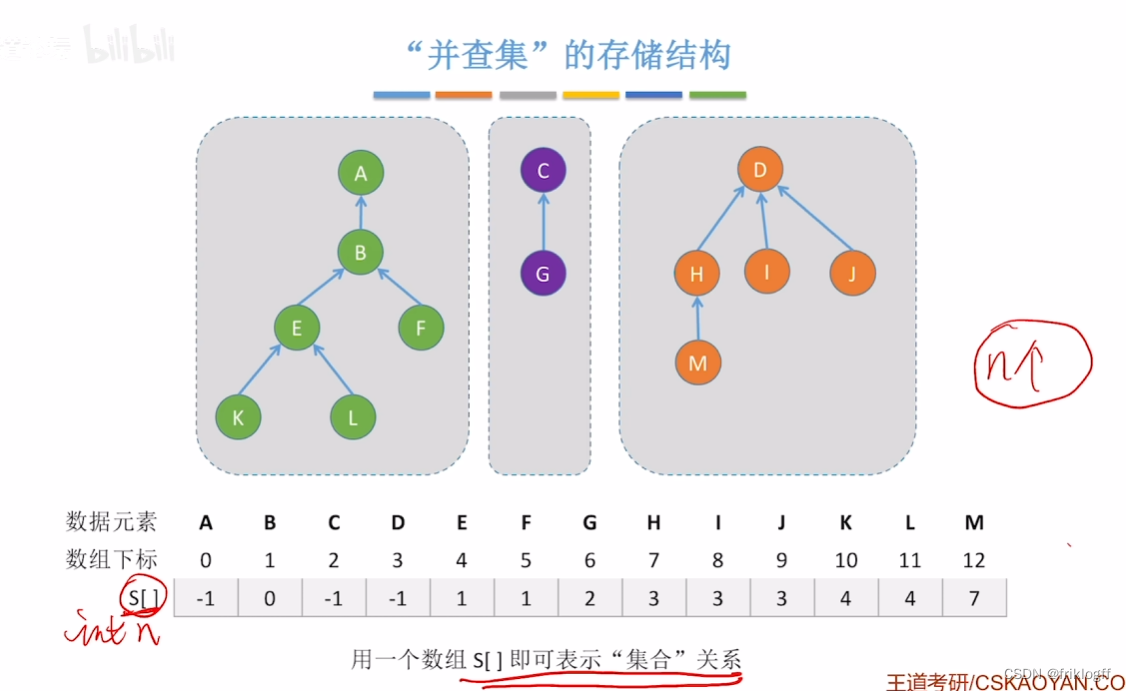
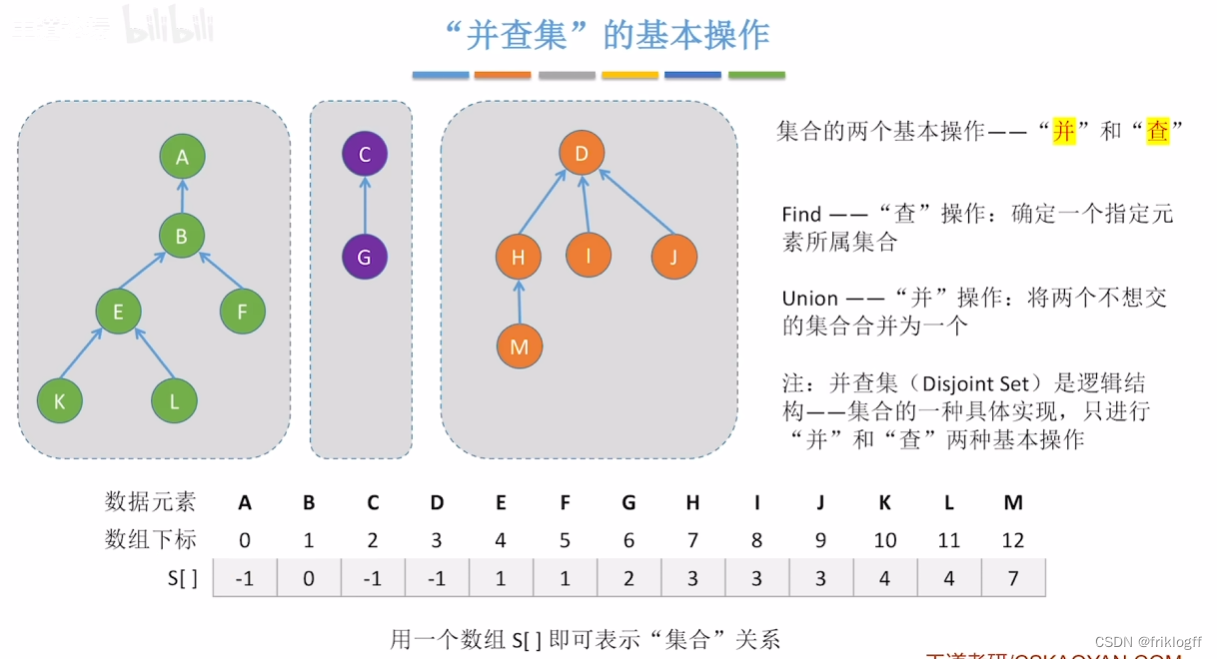
- 顺序存储，每个集合组织成一棵树，采用双亲表示法
所有表示子集合的树，构成表示全集合的森林，存放在双亲表示数组内
通常用数组元素的下标代表元素名，用根结点的下标代表子集合名

代码实现

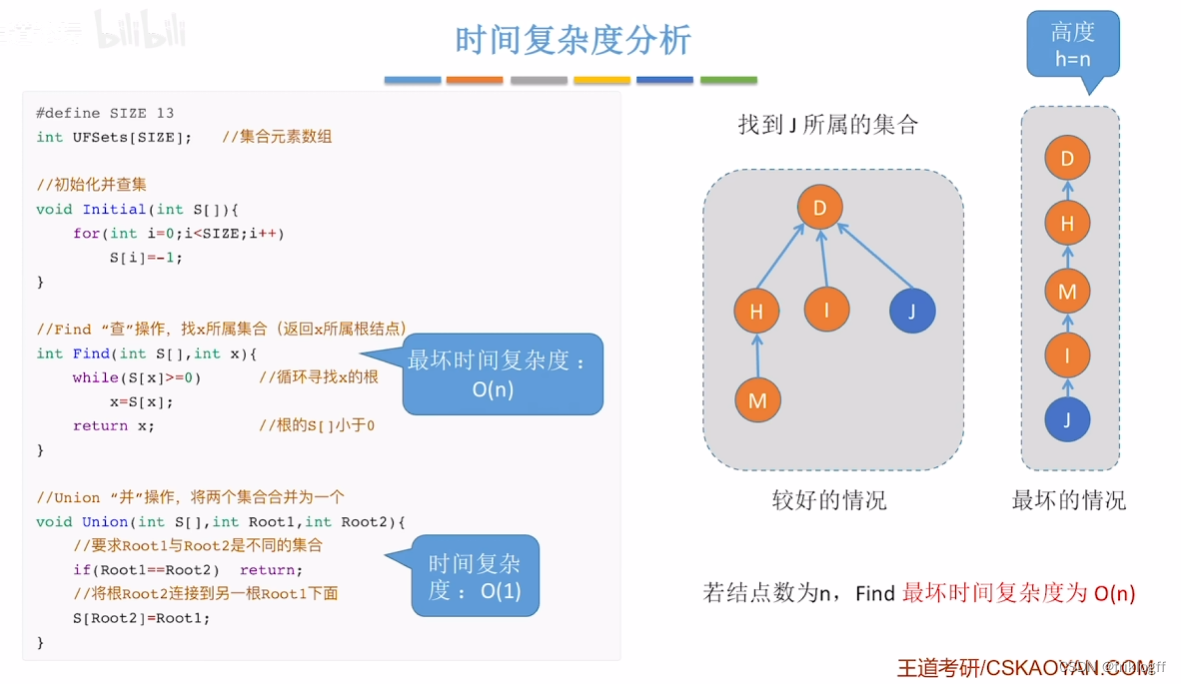
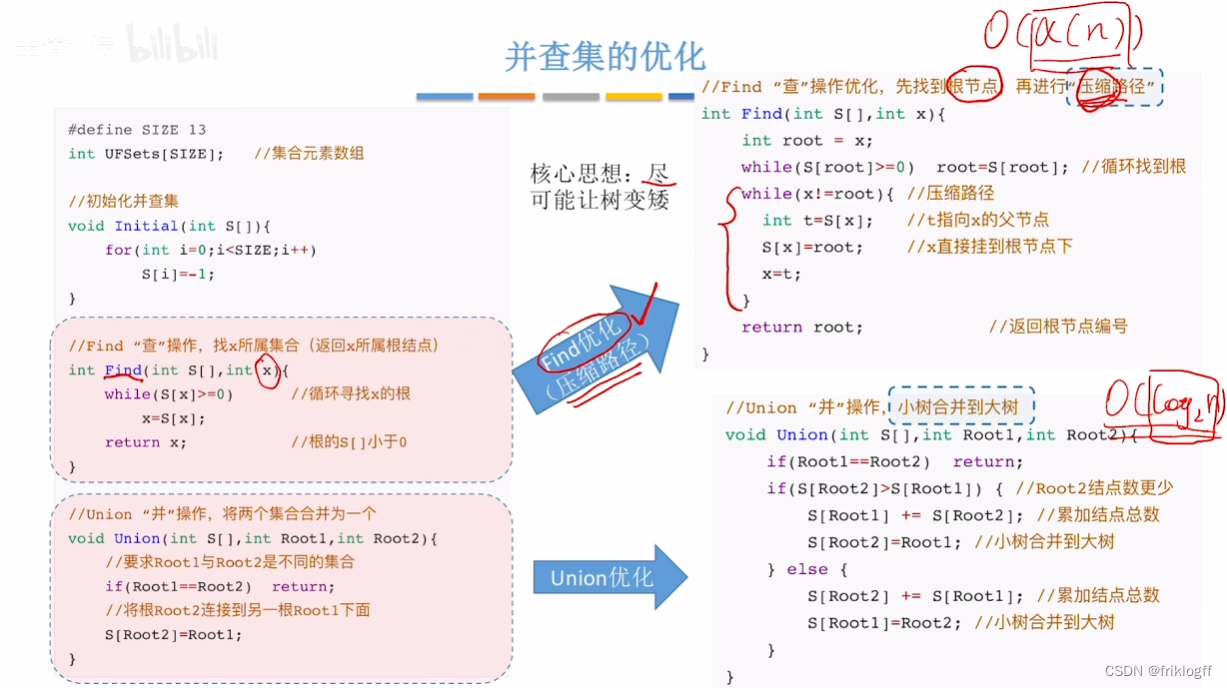
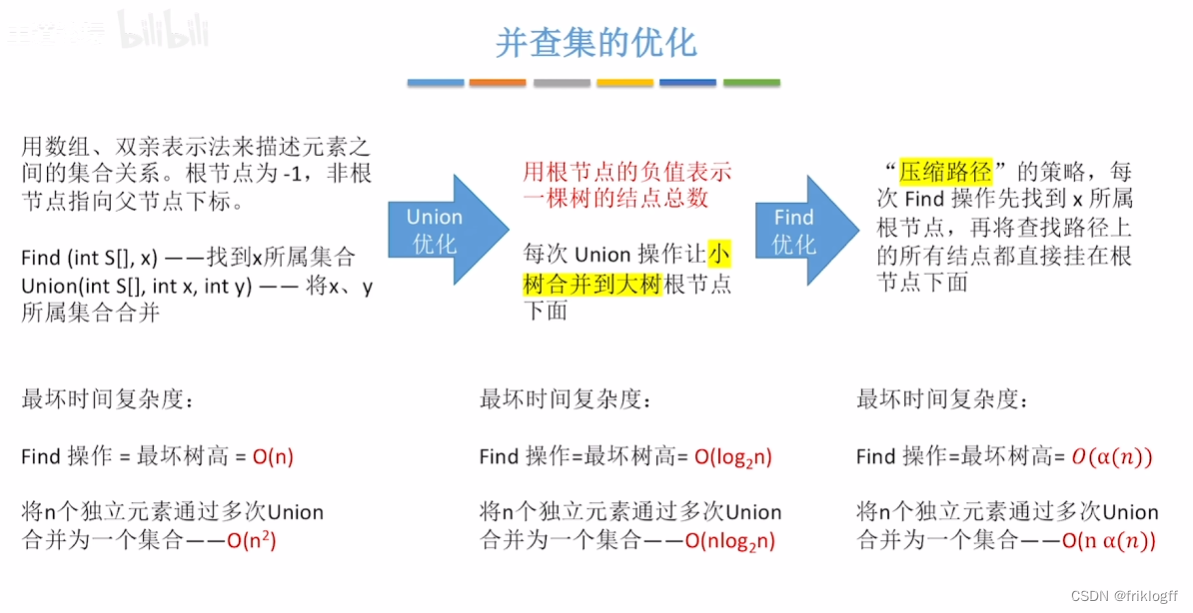
在这里插入图片描述

优化

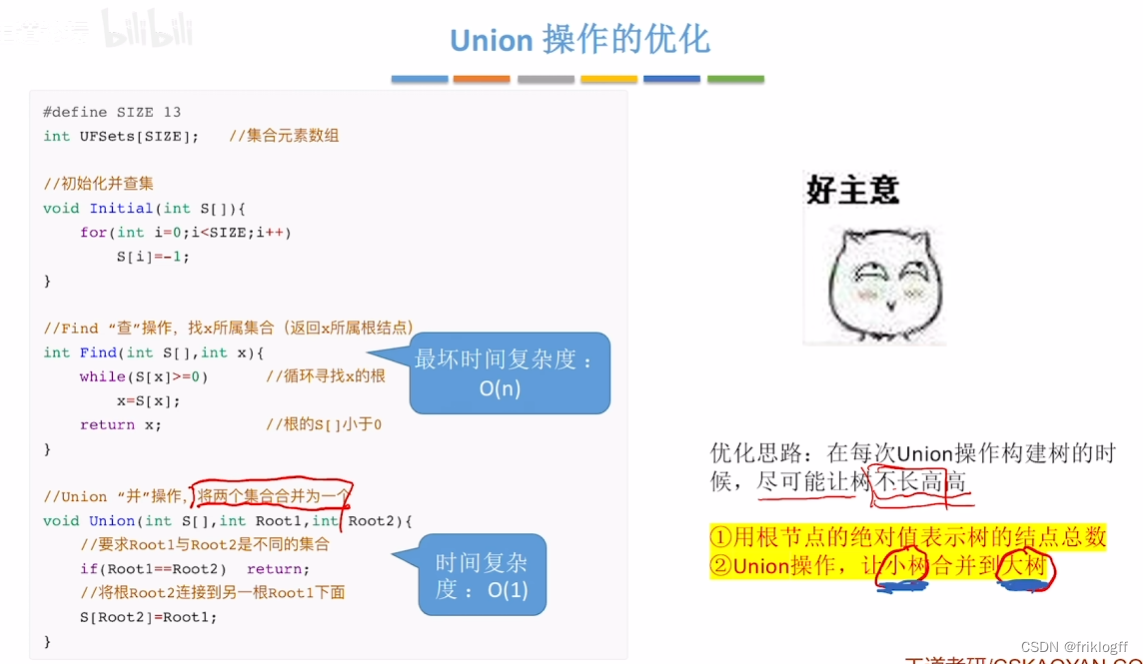
在这里插入图片描述

小树合并到大树

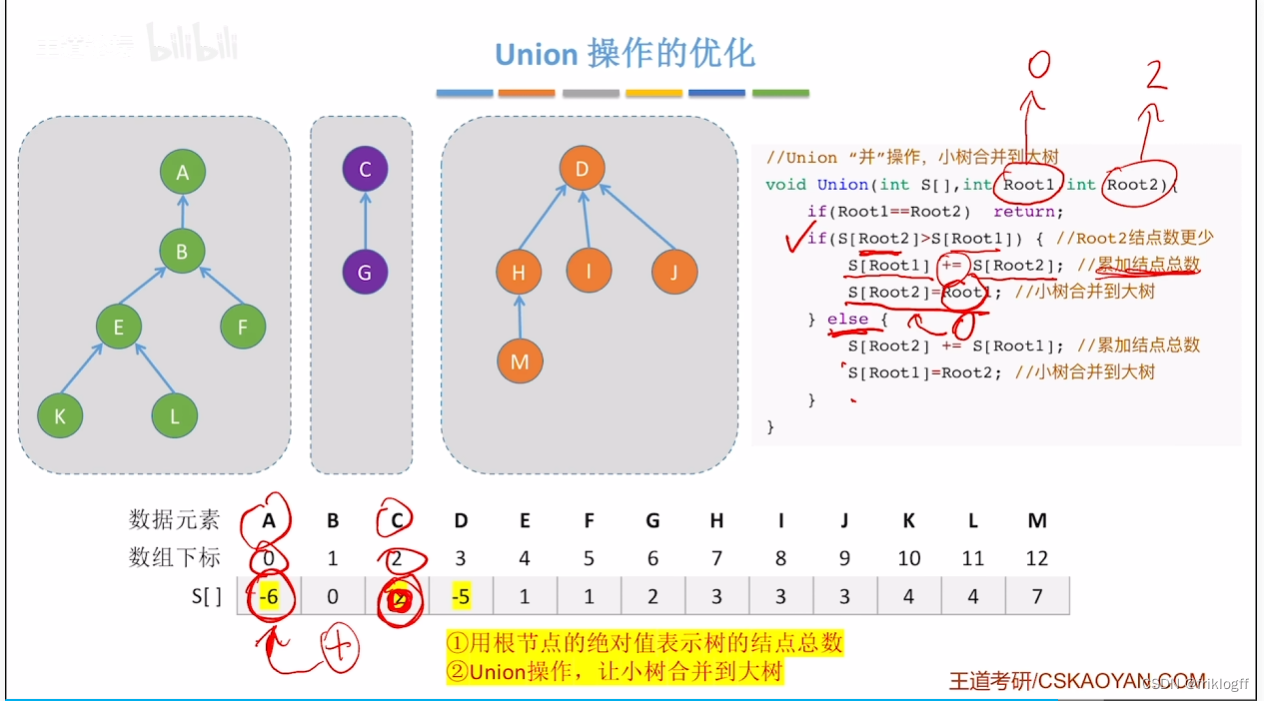
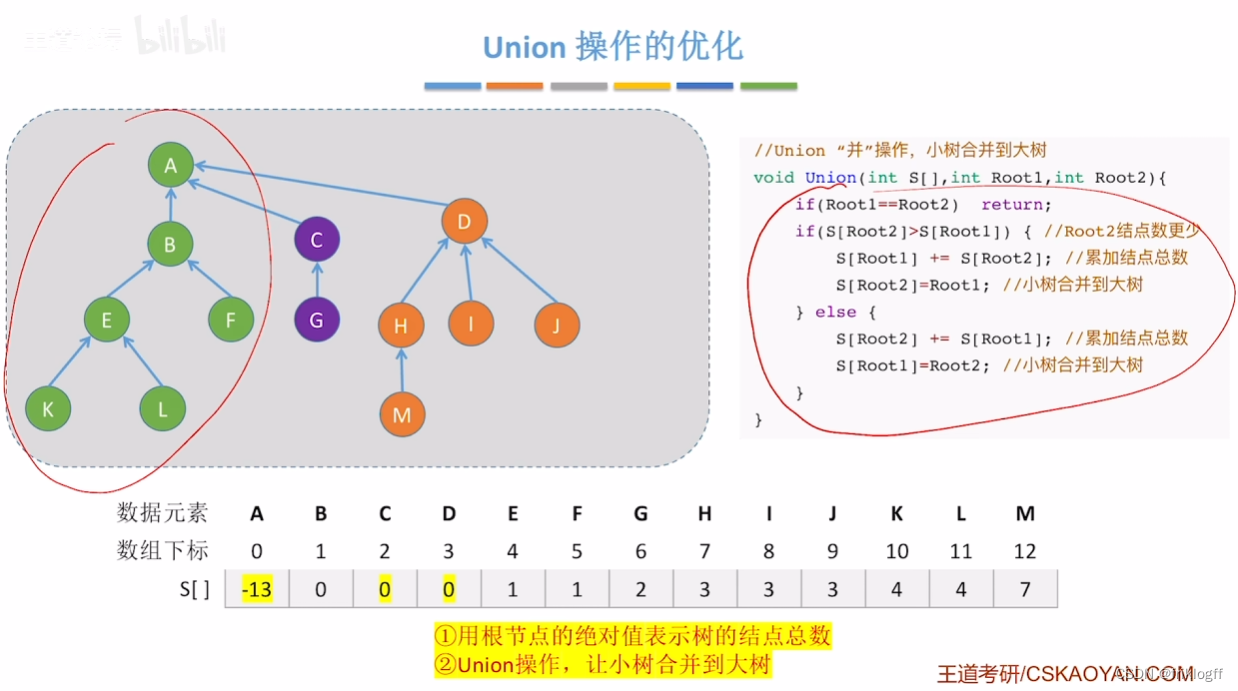
在这里插入图片描述

压缩路径

压缩路径：查找路径上所有结点都直接挂根结点

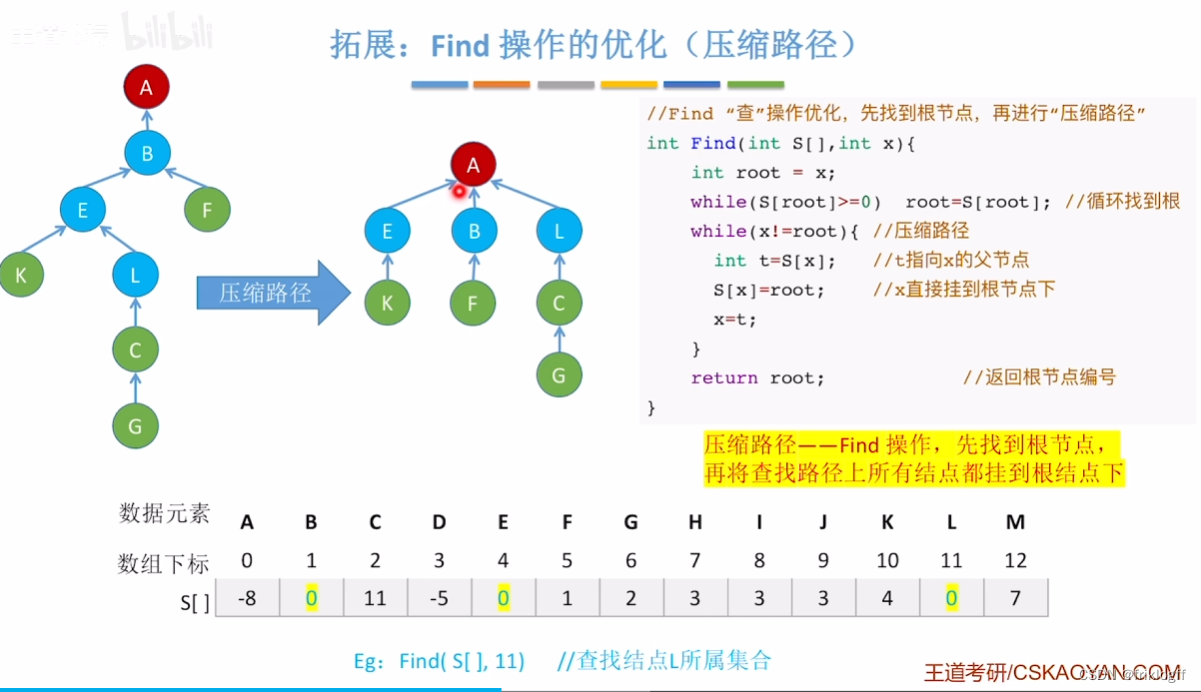
在这里插入图片描述

小结

在这里插入图片描述

(并的前提是查到根节点)

操作	查时间复杂度	并时间复杂度
基本操作	O(n)	O(n^2)
小树合并到大树	O(log2n)	O(nlog2n)
压缩路径	O(d(n))	O(nd(n))

https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
在这里插入图片描述

并查集应用

Cruskal算法、无向图的连通性、无向图是否有环

代码（巨无敌，就两行代码）

原理：每个集合用一棵树表示。树根的编号就是整个集合的编号。每个节点存储它的父节点，p[x]表示x的父节点。
血的教训!!!
注意很多题目需要在合并时去最小值，若f数组存父亲值
f[y]=min(f[x],f[y]),f[x]=min(f[x],f[y]);
每次执行find操作，确实会让每个节点直接存根节点的值，之后查找的时间复杂度接近O(1)，但仅仅是接近，不一定全是1次找到，即之后查找要用find函数而不是直接f[]找。
```
const int N=100010;
int n,m,p[N],j,k;
string str;
//并查集核心代码，就两行！！！！
int find(int x)
{if (p[x] != x) p[x] = find(p[x]);return p[x];
}
//main函数给大家可以便于理解
int main(){scanf("%d%d",&n,&m);for(int i=1;i<n+1;i++) p[i]=i;for(int i=0;i<m;i++){cin>>str>>j>>k;if(str=="M") p[find(j)]=find(k);else if(find(j)==find(k))printf("Yes\n");elseprintf("No\n");}
}
```