🎉🎉欢迎光临🎉🎉
🏅我是苏泽,一位对技术充满热情的探索者和分享者。🚀🚀
🌟特别推荐给大家我的最新专栏《数据结构与算法:初学者入门指南》📘📘
希望能和大家一起学习!共同进步!
这是苏泽的个人主页可以看到我其他的内容哦👇👇
努力的苏泽
http://suzee.blog.csdn.net

这段时间刷了几十道dp感觉人都要刷傻了 光刷题不行 还是要思考和总结 这篇纯当个人笔记
目录
动态规划的本质
动态规划其实都能归结为有限状态自动机和有向无环图
动态规划如何破局?
使用的条件
如何做?
设计状态
确定状态转移方程
确定初始状态
动态规划的几大类 +例题讲解
1. 背包问题(Knapsack Problem)
例题:0-1背包问题
2. 最长公共子序列(Longest Common Subsequence, LCS)问题
例题:最长公共子序列
3. 最大子序列和问题(Maximum Subarray Problem)
例题:最大子序列和
4. 硬币找零问题(Coin Change Problem)
例题:硬币找零
5. 矩阵链乘法问题(Matrix Chain Multiplication Problem)
例题:矩阵链乘法
坑点
容易忽略“动态”
错在把一开始的那个a[1]就当做了接龙子序列的最长序列 但实则并不一定 或者说 错在没有理解“最少”的含义
动态规划的本质
动态规划其实都能归结为有限状态自动机和有向无环图
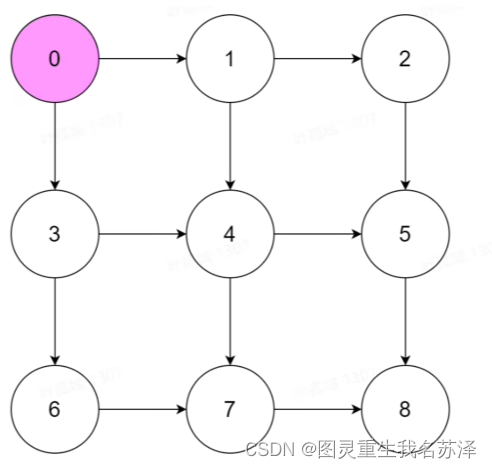
动态规划可以被视为一种有限状态自动机,其中每个状态代表了问题的一个子集,状态之间的转移代表了子问题之间的关联。在有向无环图(Directed Acyclic Graph,简称DAG)中,每个节点代表一个状态,而边则代表了状态之间的转移关系。通过这种方式,动态规划将问题转化为在一个DAG上寻找最优路径的问题。
动态规划如何破局?
动态规划的关键在于如何设计状态和状态转移方程,以及如何确定初始状态。以下是动态规划的一般步骤:
使用的条件
在应用动态规划之前,我们需要确保问题满足以下条件:
- 最优化原理:问题能够在其子问题的基础上构造出最优解。
- 重叠子问题:问题可以被分解为相互重叠的子问题,且子问题的解可以被重复使用。
- 有限状态数:状态的数量是有限的,且满足状态数*状态转移数<10^6的条件,以保证算法的可行性。
如何做?
设计状态
设计状态是动态规划中最为关键的一步。状态应该能够唯一地表示问题的某个阶段,同时包含所有必要的信息以决定下一步的行动。状态的设计需要根据具体问题的特点来进行,常见的状态表示方法包括:
- 位置:在序列问题中,可以用位置来表示状态。
- 剩余元素:在涉及选择的问题中,可以用剩余可选元素的数量来表示状态。
- 部分结果:在需要构造结果的问题中,可以用已经得到的部分结果来表示状态。
确定状态转移方程
状态转移方程描述了状态之间的转移关系,它定义了如何从一个或多个状态得到新的状态。状态转移方程的设计需要满足最优化原理,确保能够从子问题的最优解得到原问题的最优解。 常见的状态转移方程类型包括:
- 相加或相乘:当问题涉及到数值的累加或累乘时。
- 选择:当问题需要在多个选项中选择一个最优的选项时。
- 条件转移:当状态转移依赖于某些条件或属性时。
确定初始状态
初始状态是动态规划的起点,它通常代表了问题规模最小的情况下的状态。确定初始状态需要根据问题的具体背景和定义来进行。
动态规划的几大类 +例题讲解
1. 背包问题(Knapsack Problem)
背包问题是一种典型的组合优化问题,通常描述为有一个可以装载重量为W的背包和一组物品,每个物品有自己的重量和价值,目标是选择物品的组合,使得背包中物品的总重量不超过W,且总价值最大。
例题:0-1背包问题
描述:给定n个物品,每个物品有自己的重量w[i]和价值v[i],以及一个最大承重W的背包。求解如何选择物品放入背包,使得背包中物品的总价值最大。
解题思路:定义dp[i][j]为前i个物品中,能够装入容量为j的背包的最大价值。状态转移方程为:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i])
其中,dp[i-1][j]表示不选择第i个物品,而dp[i-1][j-w[i]] + v[i]表示选择第i个物品。
2. 最长公共子序列(Longest Common Subsequence, LCS)问题
LCS问题是一种经典的字符串匹配问题,通常描述为有两个字符串,求解这两个字符串的最长公共子序列的长度。
例题:最长公共子序列
描述:给定两个字符串s1和s2,求解它们的最长公共子序列。
解题思路:定义dp[i][j]为s1的前i个字符和s2的前j个字符的最长公共子序列的长度。状态转移方程为:
if s1[i-1] == s2[j-1] dp[i][j] = dp[i-1][j-1] + 1 else dp[i][j] = max(dp[i-1][j], dp[i][j-1])
其中,相等的情况表示找到了一个公共字符,不相等的情况则取两个方向的最大值。
3. 最大子序列和问题(Maximum Subarray Problem)
最大子序列和问题是一种数组优化问题,通常描述为给定一个整数数组,找到一个连续子数组,使得其和最大。
例题:最大子序列和
描述:给定一个整数数组nums,返回其中最大子序列的和。
解题思路:定义tempSum为当前子数组的和,maxSum为当前找到的最大子序列和。遍历数组,对于每个元素,更新tempSum和maxSum:
if tempSum < 0 tempSum = nums[i] else tempSum += nums[i] if tempSum > maxSum maxSum = tempSum
这种方法的时间复杂度为O(n)。
4. 硬币找零问题(Coin Change Problem)
硬币找零问题是一种货币找零问题,通常描述为给定不同面额的硬币和一个总金额,求解凑成总金额所需的最少硬币个数。
例题:硬币找零
描述:给定不同面额的硬币coins和一个总金额amount,返回凑成总金额所需的最少硬币个数。
解题思路:定义dp[i]为组合成金额i所需的最少硬币个数。状态转移方程为:
dp[i] = min(dp[i], dp[i-c] + 1),对于所有c属于coins
其中,dp[i-c] + 1表示使用面额为c的硬币凑成金额i。
5. 矩阵链乘法问题(Matrix Chain Multiplication Problem)
矩阵链乘法问题是一种动态规划在矩阵乘法中的应用问题,通常描述为给定一系列矩阵,求解将它们乘在一起的最小计算成本。
例题:矩阵链乘法
描述:给定一系列矩阵的维度p[1...n],其中p[i]表示第i个矩阵的行数和列数,求解按照哪种顺序乘这些矩阵,使得计算成本最小。
解题思路:定义dp[i][j]为计算矩阵链p[i...j]的最小成本。状态转移方程为:
dp[i][j] = min{dp[k][j] + dp[i][k-1] + p[i]*p[k]*p[j]》,对于所有i ≤ k < j
其中,dp[k][j]和dp[i][k-1]表示分别计算矩阵链p[i...k]和p[k+1...j]的成本,而p[i]*p[k]*p[j]是这两个链相乘时的计算成本。
坑点
容易忽略“动态”
把一个线性的状态作为“固定点” 一直延展
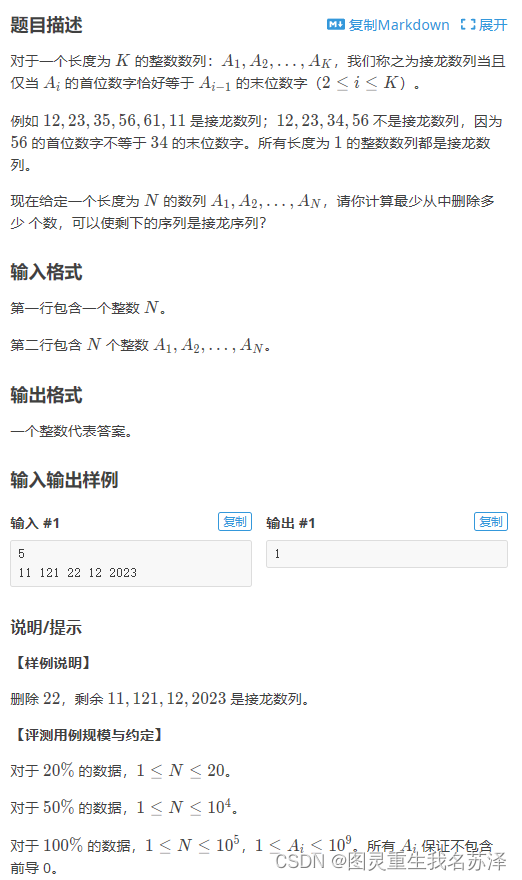
就像这道 接龙数列:P9242 [蓝桥杯 2023 省 B] 接龙数列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
我一开始的错误
public class MyWrong {public static void main(String[] args) {Scanner in=new Scanner(System.in);int N=in.nextInt();long[] a=new long[N+1];long length =0;for (int i = 1; i <=N ; i++) {a[i]=in.nextInt();length++;}long ans=0;int now=getHead(a[1]);for (int i = 1; i <=N ; i++) {//错在把一开始的那个a[1]就当做了接龙子序列的最长序列// 但实则并不一定 或者说 错在没有理解“最少”的含义if (now==getHead(a[i])){ans++;now=(int)a[i]%10;}}System.out.println(length-ans);}static public int getHead(long l){while (l>=10){l/=10;}return (int)l;}
}