自动驾驶中的多目标跟踪:第三篇

附赠自动驾驶学习资料和量产经验：链接

在前一节，我们回顾了贝叶斯滤波，并给出了线性高斯条件下的闭式解–卡尔曼滤波。在这一节，我们来讨论杂波背景下的单目标滤波问题。

模型

（三）杂波模型

下表给出的是生成上述杂波量测的算法

至此，模型的完善到此为止。在下一部分，我们来看贝叶斯递推过程。

---

贝叶斯递推过程

(1) 预测过程

预测过程仍然与上一节一样，使用切普曼-柯尔莫哥洛夫方程（Chapman-Kolmogorov equation)对目标状态进行预测

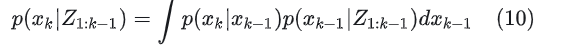
(2) 更新过程

通过下图来观察后验中数据关联假设数的变化，图中横坐标是时间，每一个时间点上对应着量测，其中星号表示真实接收到的量测，圆圈表示目标漏检。 k=3 时后验概率中数据关联假设的个数即为图中从时刻1到时刻3的总路径数。

数据关联示意图（圆圈代表漏警，星号代表某一量测）

很显然，式（15）给出的解是无法应用的(intractable)，因为数据关联假设数随着时间的增长而激增。因此，不同滤波算法采用不同近似手段去逼近真实后验。

---

在下一节我会介绍线性高斯条件下后验概率的具体形式 ，并给出最近邻算法(NN, nearest neighbor)、概率数据互联算法(PDA,probabilistic data association)和高斯和滤波算法(GSF, Gaussian sum filter)。我们会看到，三种算法的区别在于对后验概率的近似手段。

---

附录

量测似然函数的推导