主流排序简单集合

排序算法集合

选择排序

图解：
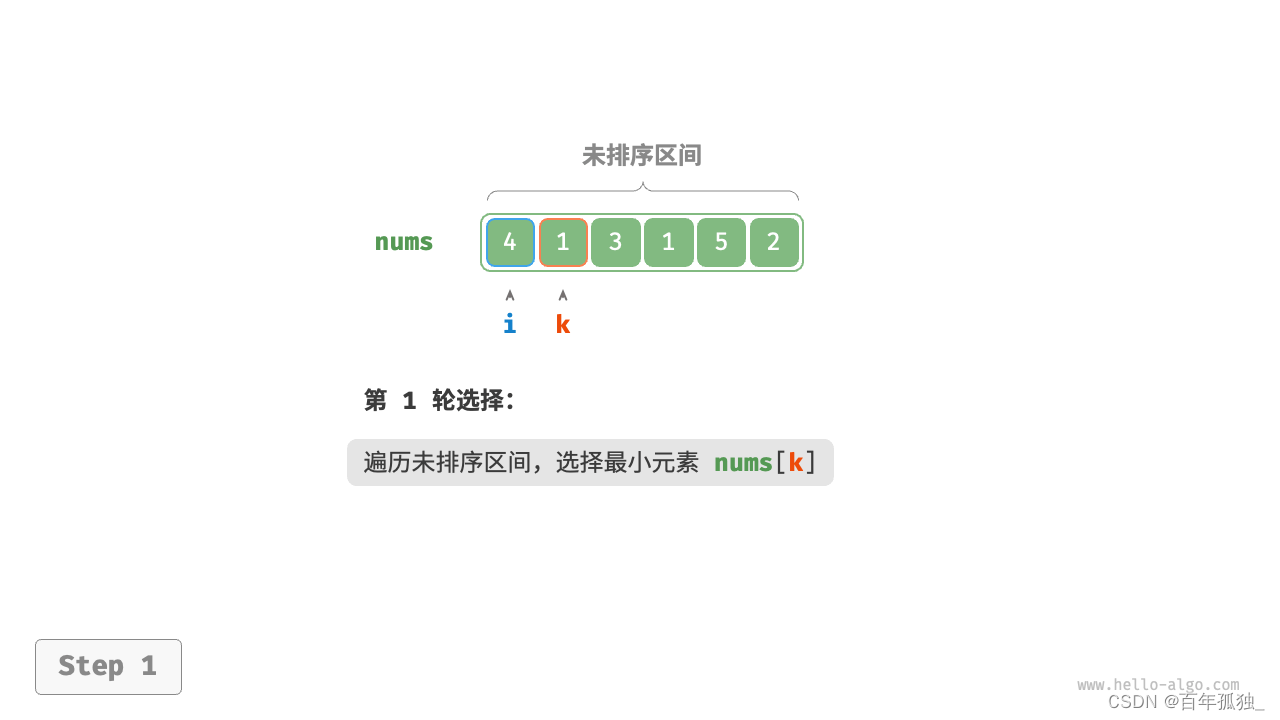
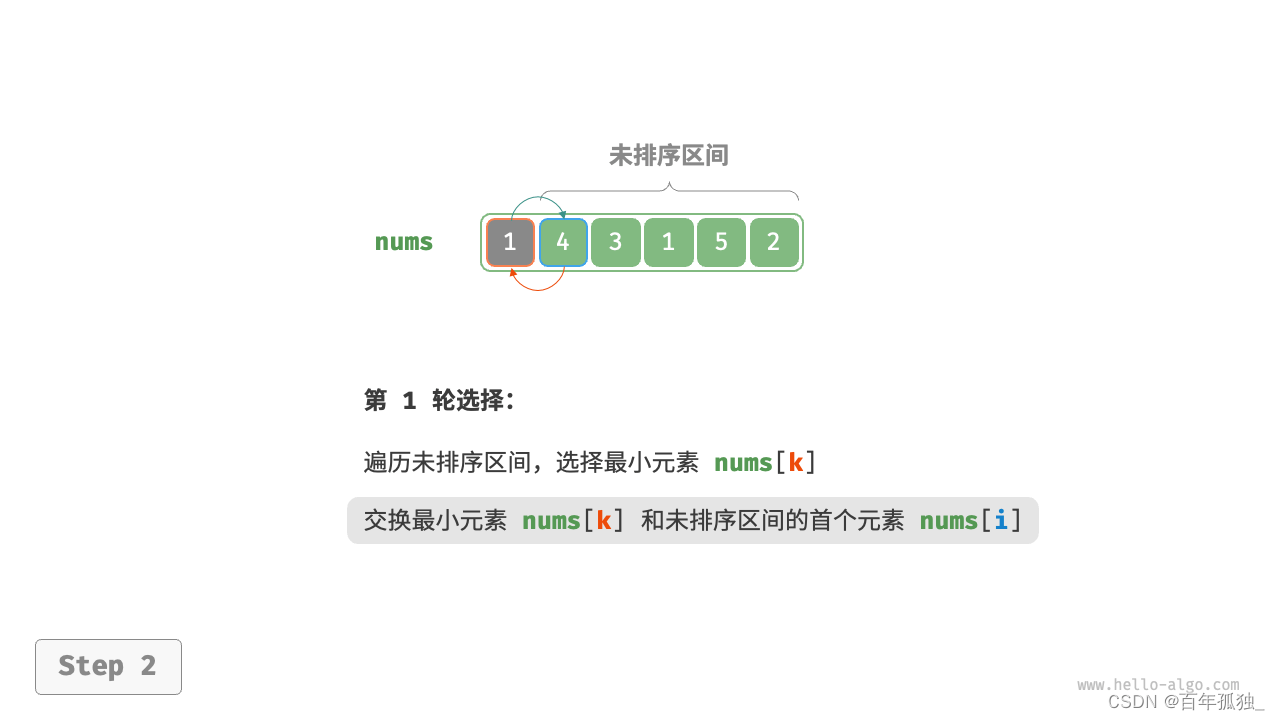
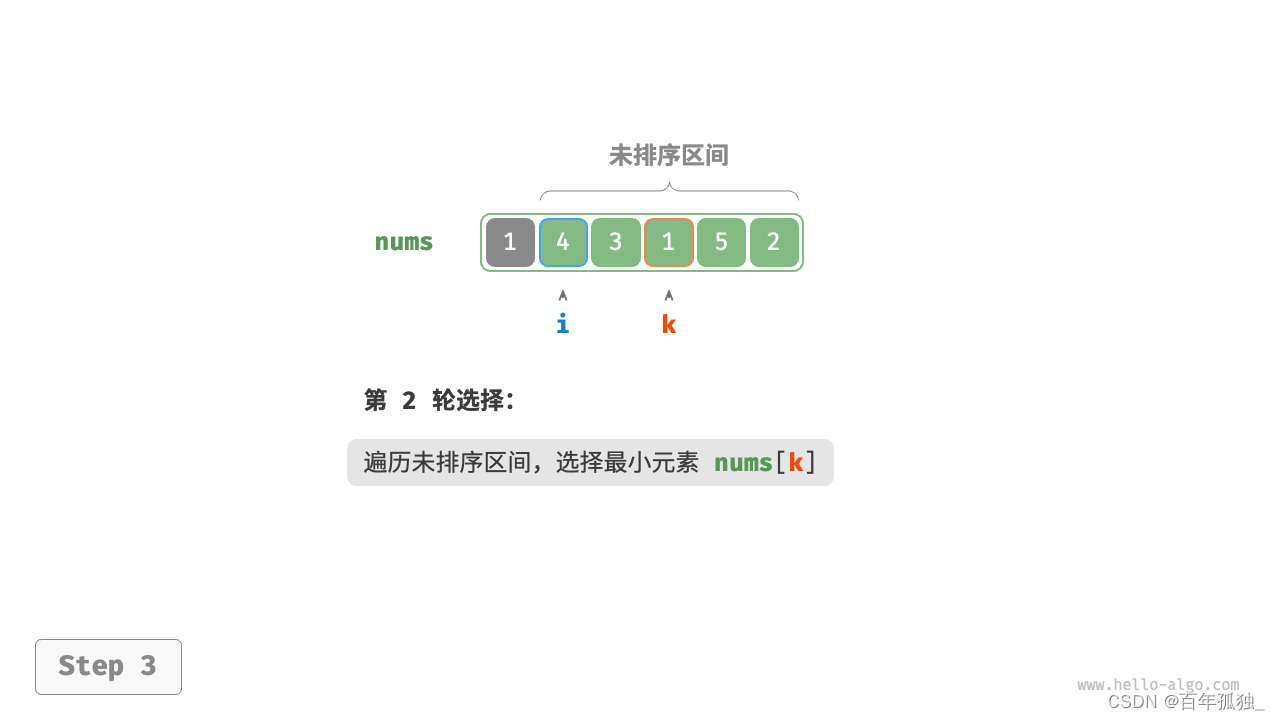
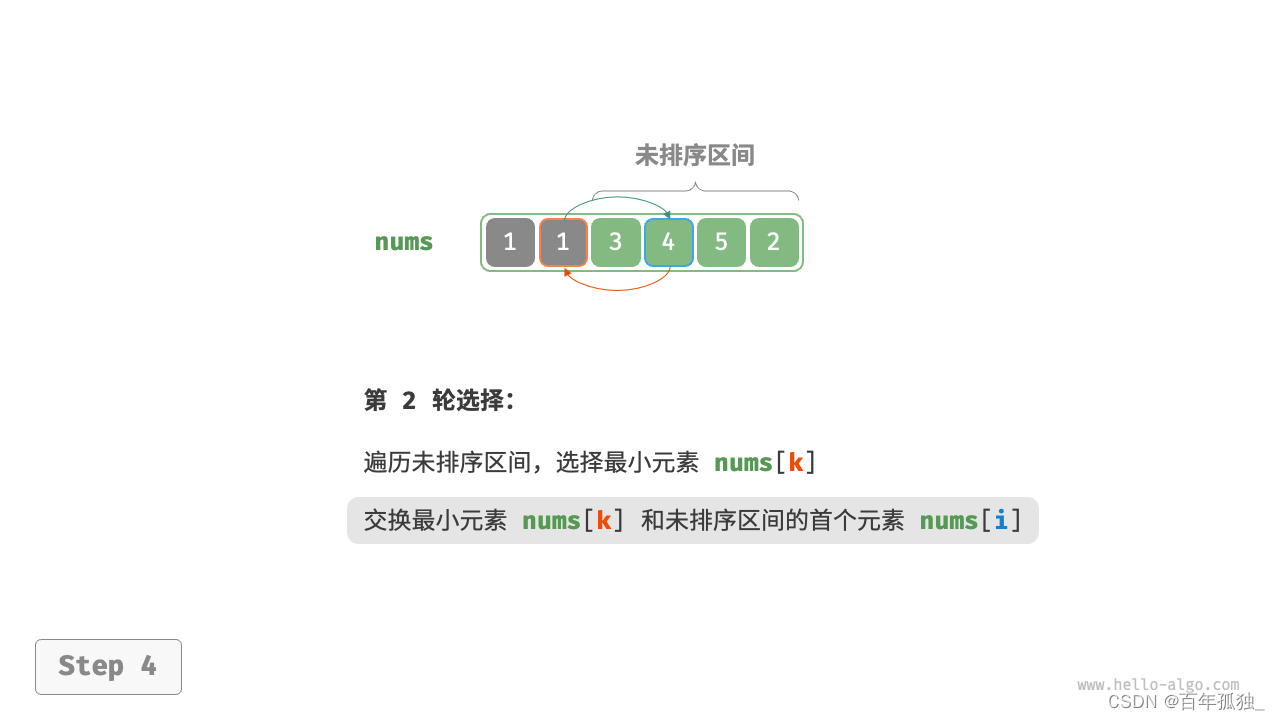
以此类推直至

/*选择排序*/
void select_sort(vector<int>& nums) {/*选取一个基准元素逐个与后面的比较*/for (int i = 0; i < nums.size() - 1-1; i++) {int min = i;/*定义随之变化的基准元素*/for (int j = i + 1; j < nums.size() - 1; j++) {if (nums[i] > nums[j]) {swap(nums[i], nums[j]);//交换元素}}}
}/* 选择排序 */  官方正解
void selectionSort(vector<int>& nums) {int n = nums.size();// 外循环：未排序区间为 [i, n-1]for (int i = 0; i < n - 1; i++) {// 内循环：找到未排序区间内的最小元素int k = i;for (int j = i + 1; j < n; j++) {if (nums[j] < nums[k])k = j; // 记录最小元素的索引}// 将该最小元素与未排序区间的首个元素交换swap(nums[i], nums[k]);}
}

冒泡排序（经典）

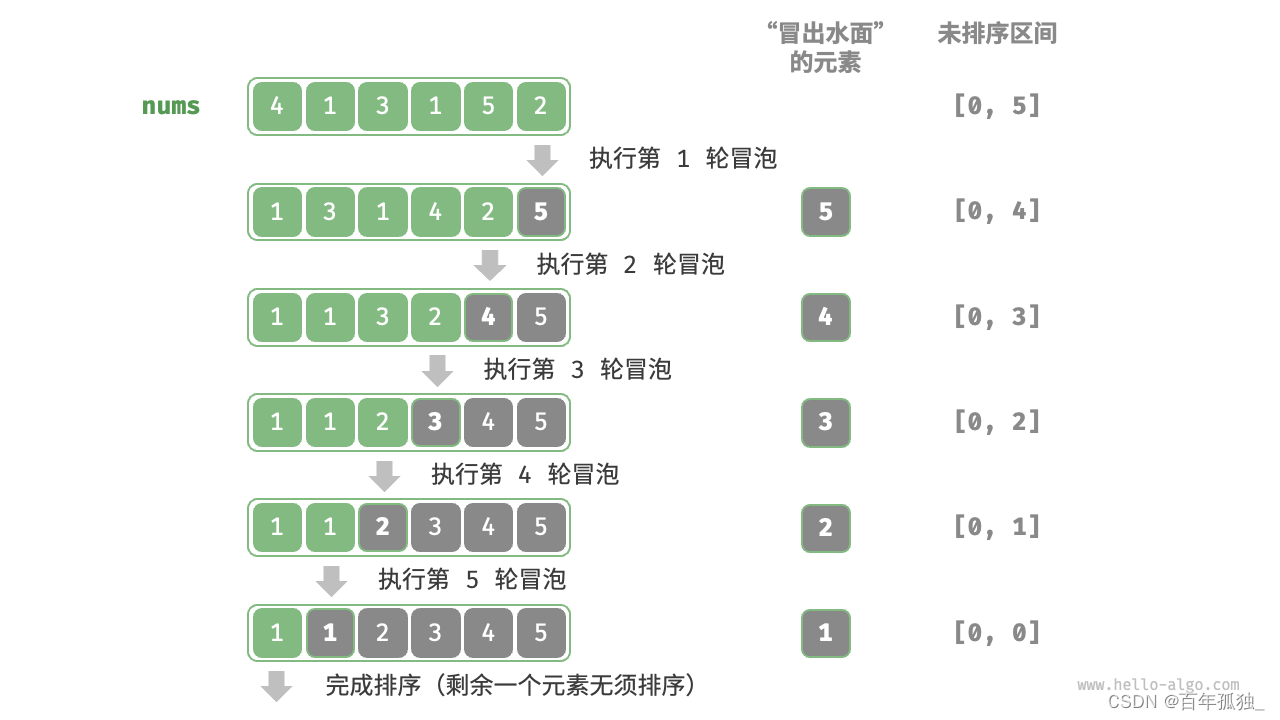
在这里插入图片描述

/* 冒泡排序 */
void bubbleSort(vector<int>& nums) {// 外循环：未排序区间为 [0, i]for (int i = nums.size() - 1; i > 0; i--) {// 内循环：将未排序区间 [0, i] 中的最大元素交换至该区间的最右端for (int j = 0; j < i; j++) {if (nums[j] > nums[j + 1]) {// 交换 nums[j] 与 nums[j + 1]// 这里使用了 std::swap() 函数swap(nums[j], nums[j + 1]);}}}
}void test() {vector<int> nums = { 4,23,6,12,56,78,2,3,5,76 };//select_sort(nums);bubbleSort(nums);for (int num : nums) {cout << num << " ";}
}

插入排序

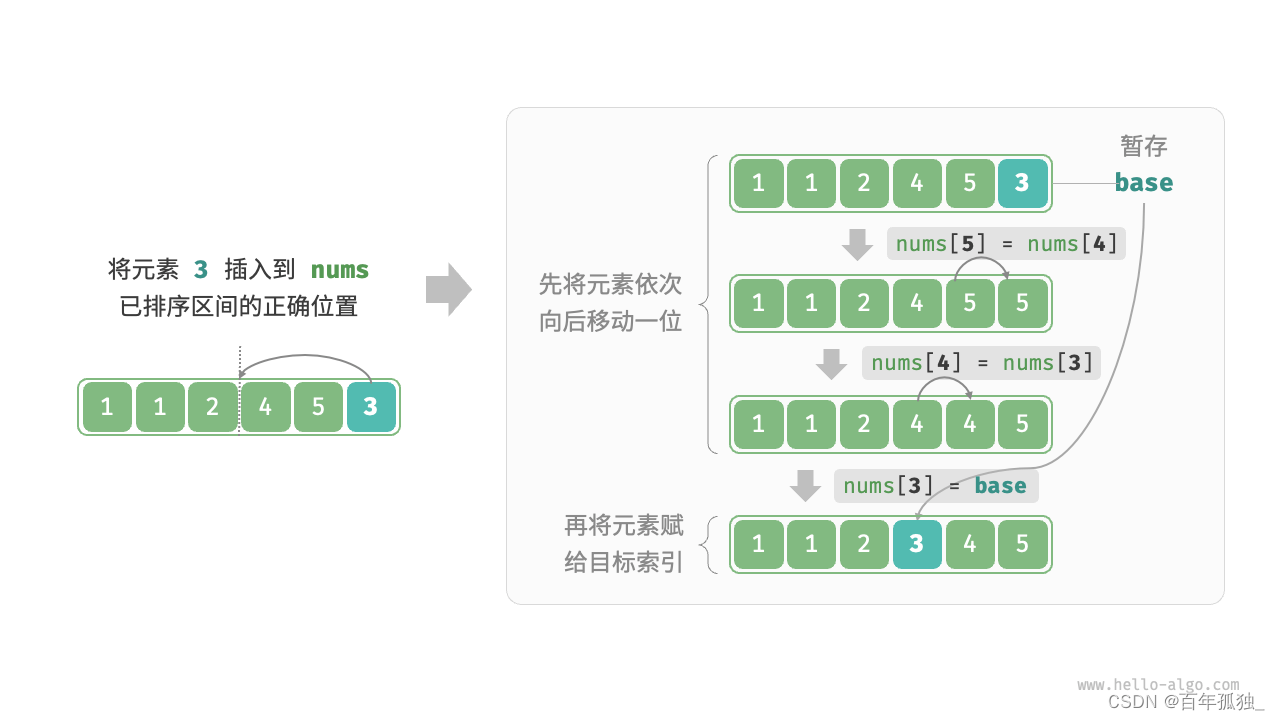
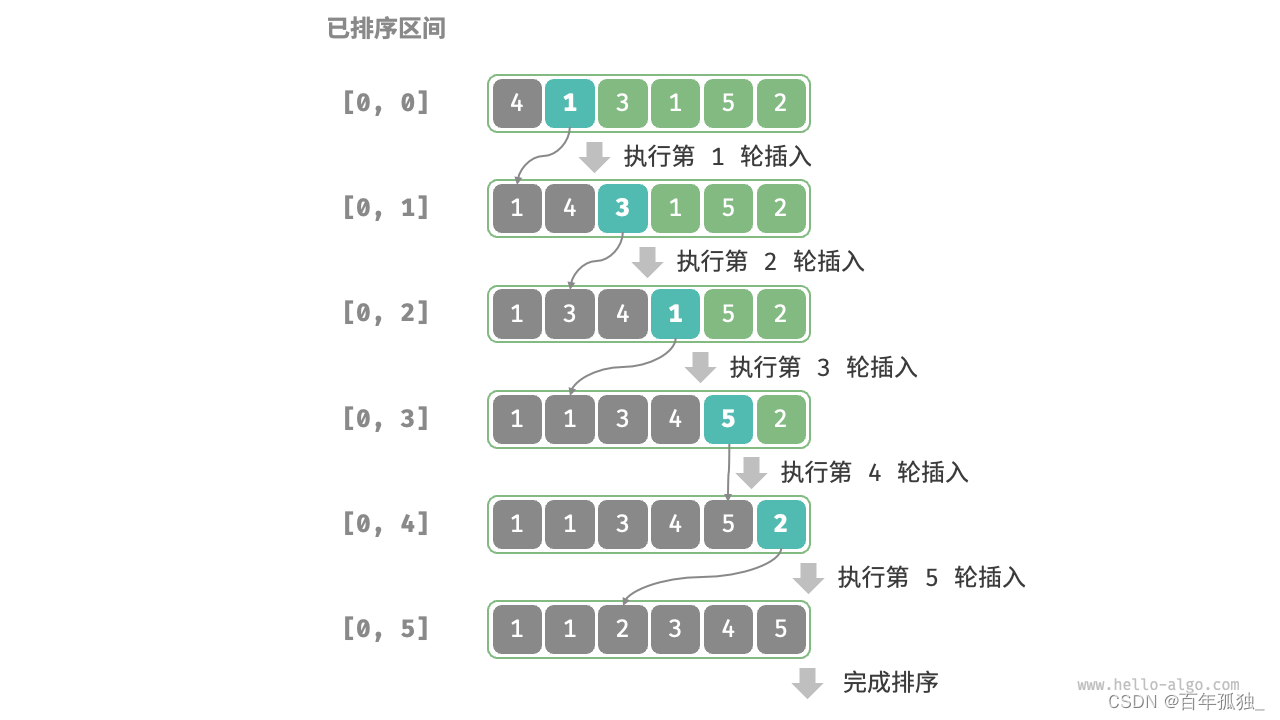
在这里插入图片描述

/* 插入排序 */
void insertionSort(vector<int> &nums) {// 外循环：已排序区间为 [0, i-1]for (int i = 1; i < nums.size(); i++) {int base = nums[i], j = i - 1;// 内循环：将 base 插入到已排序区间 [0, i-1] 中的正确位置while (j >= 0 && nums[j] > base) {nums[j + 1] = nums[j]; // 将 nums[j] 向右移动一位j--;}nums[j + 1] = base; // 将 base 赋值到正确位置}
}

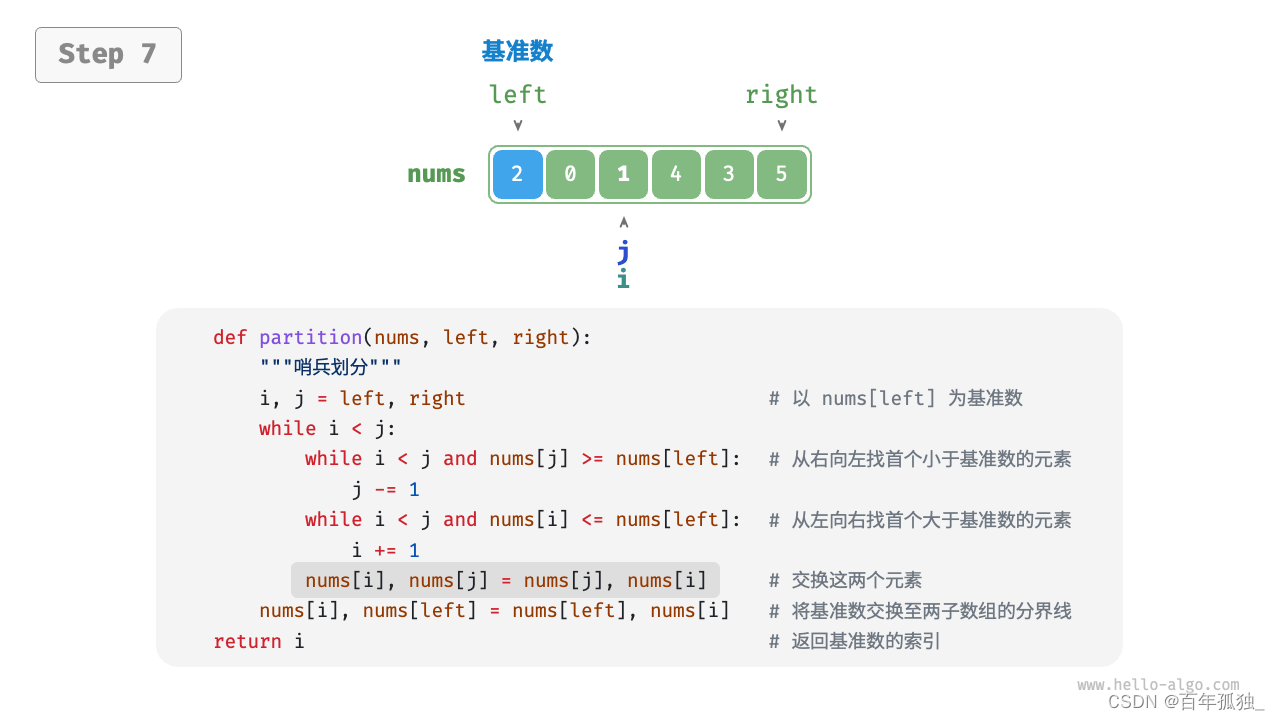
快速排序

重点理解反复熟悉
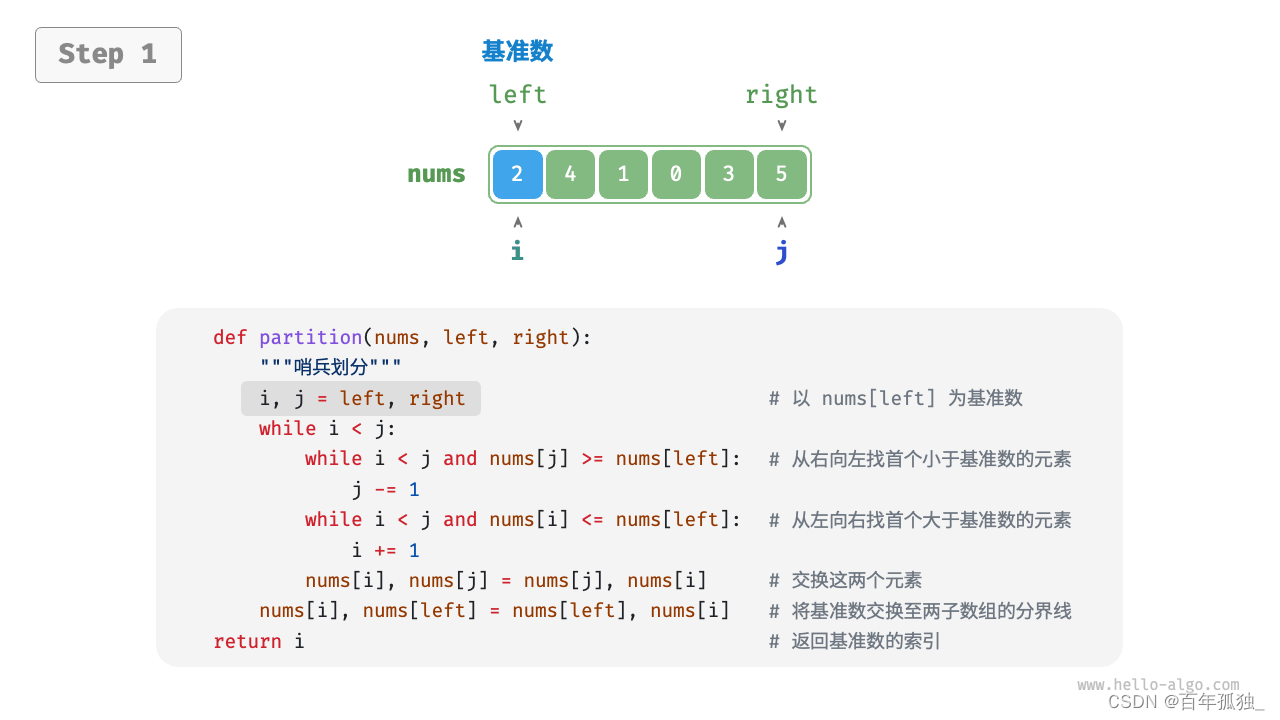
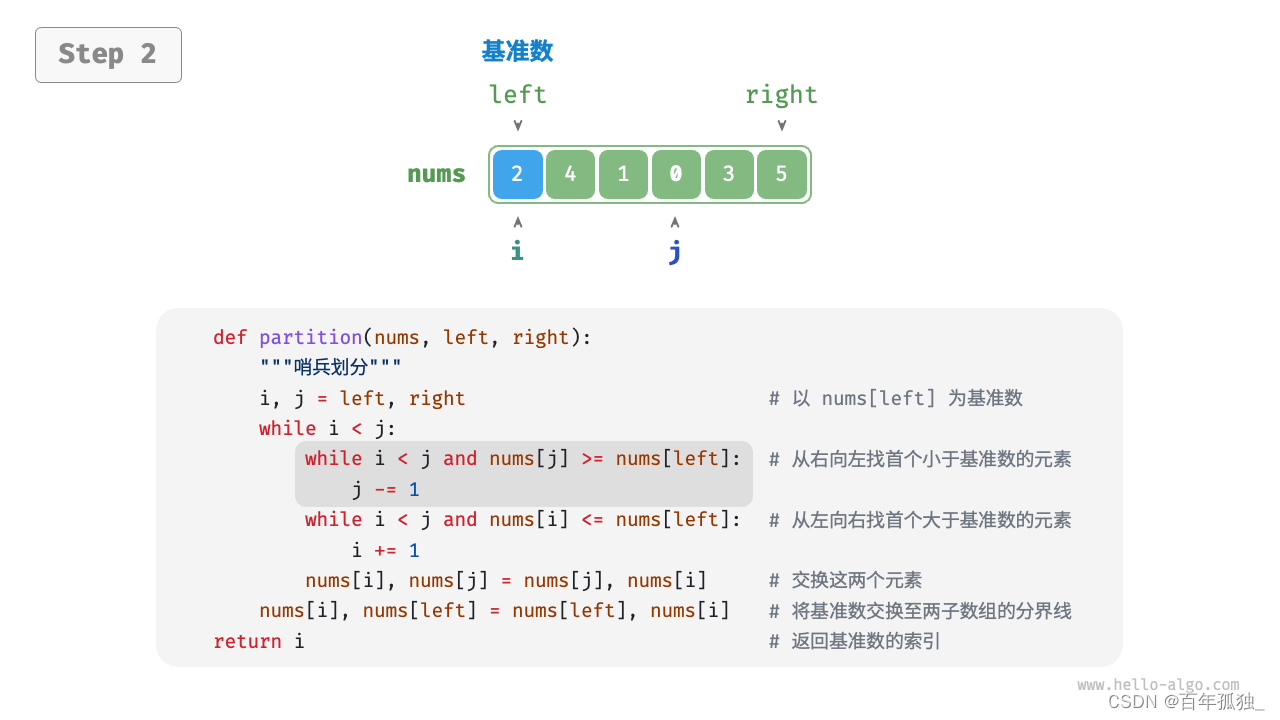
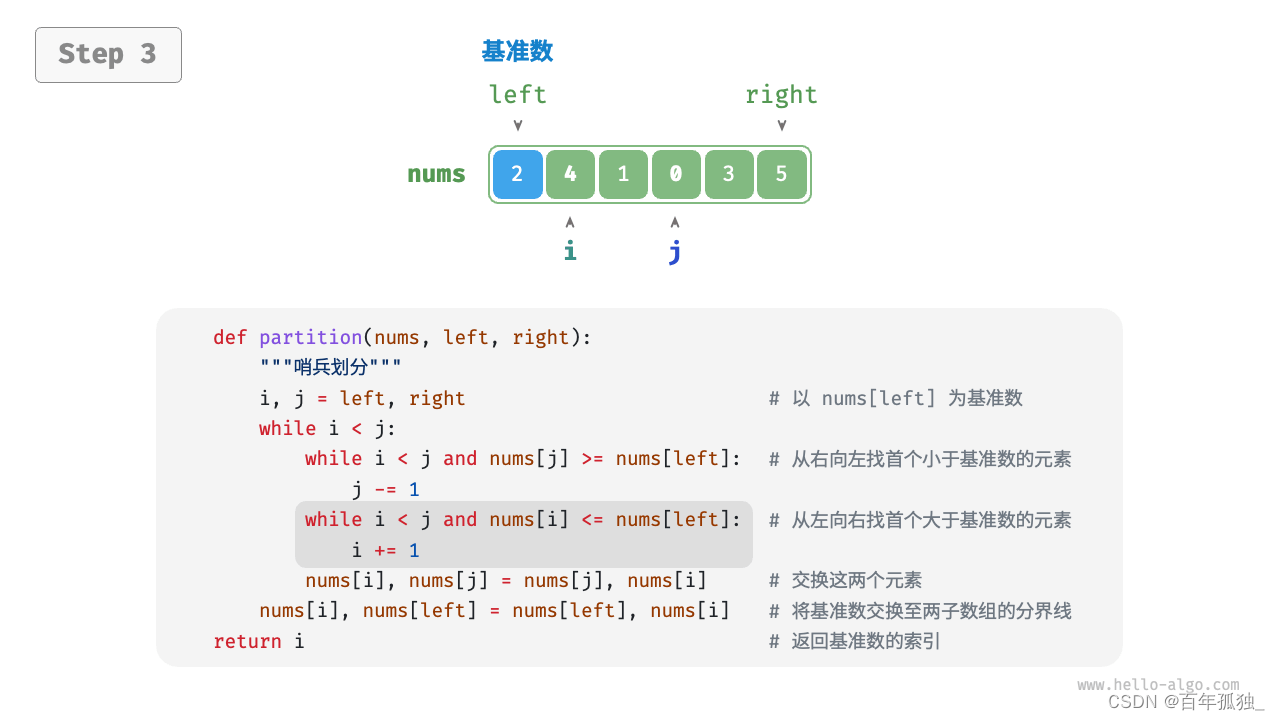
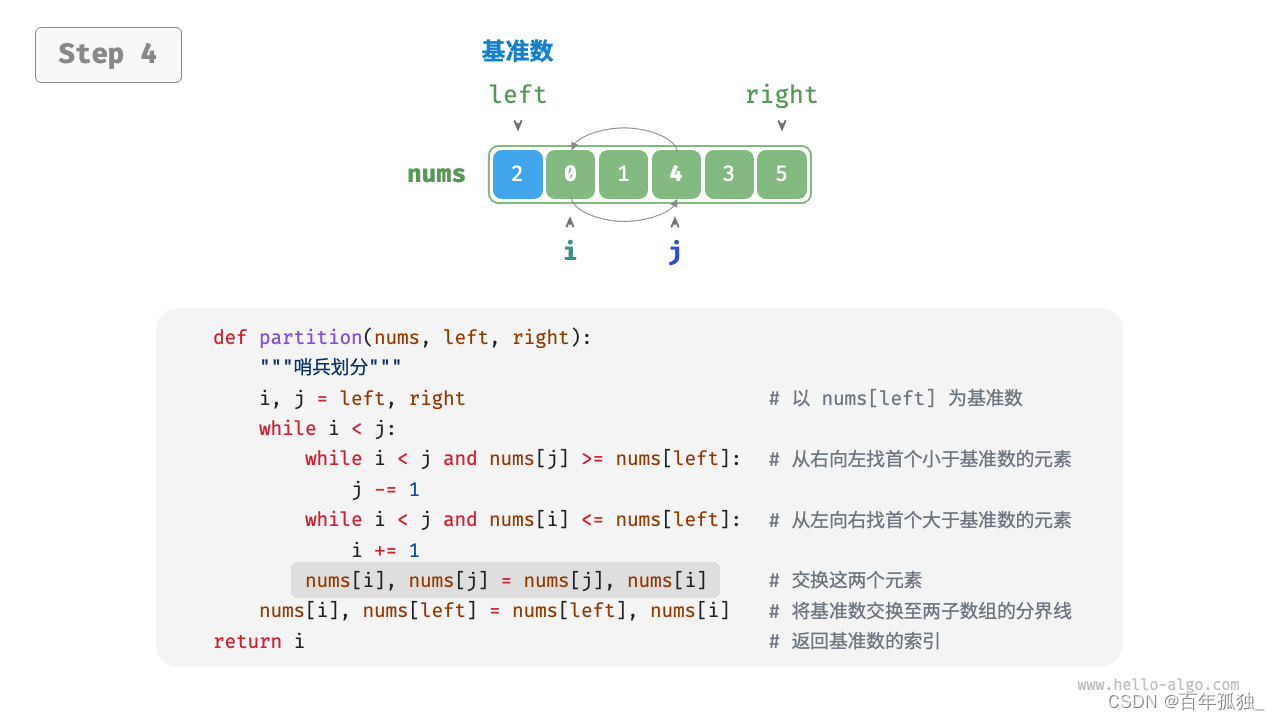
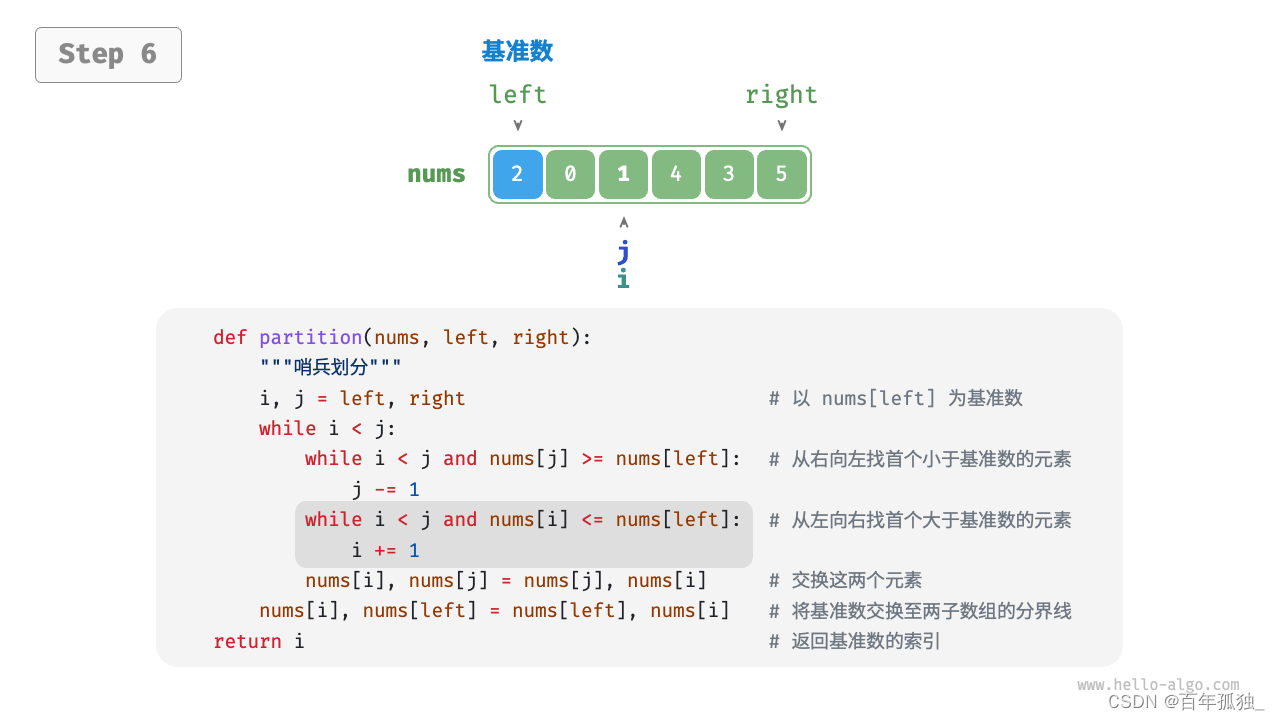
在这里插入图片描述

/* 元素交换 */
void swap(vector<int>& nums, int i, int j) {int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;
}/* 哨兵划分 */
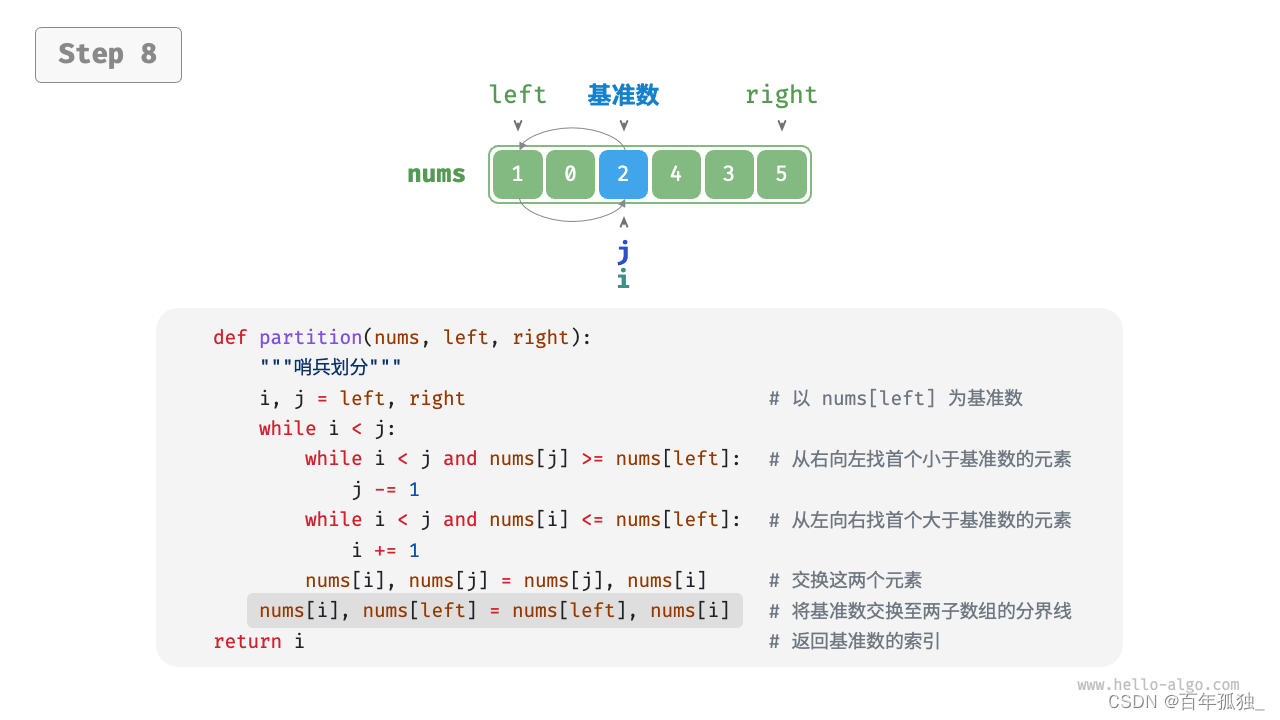
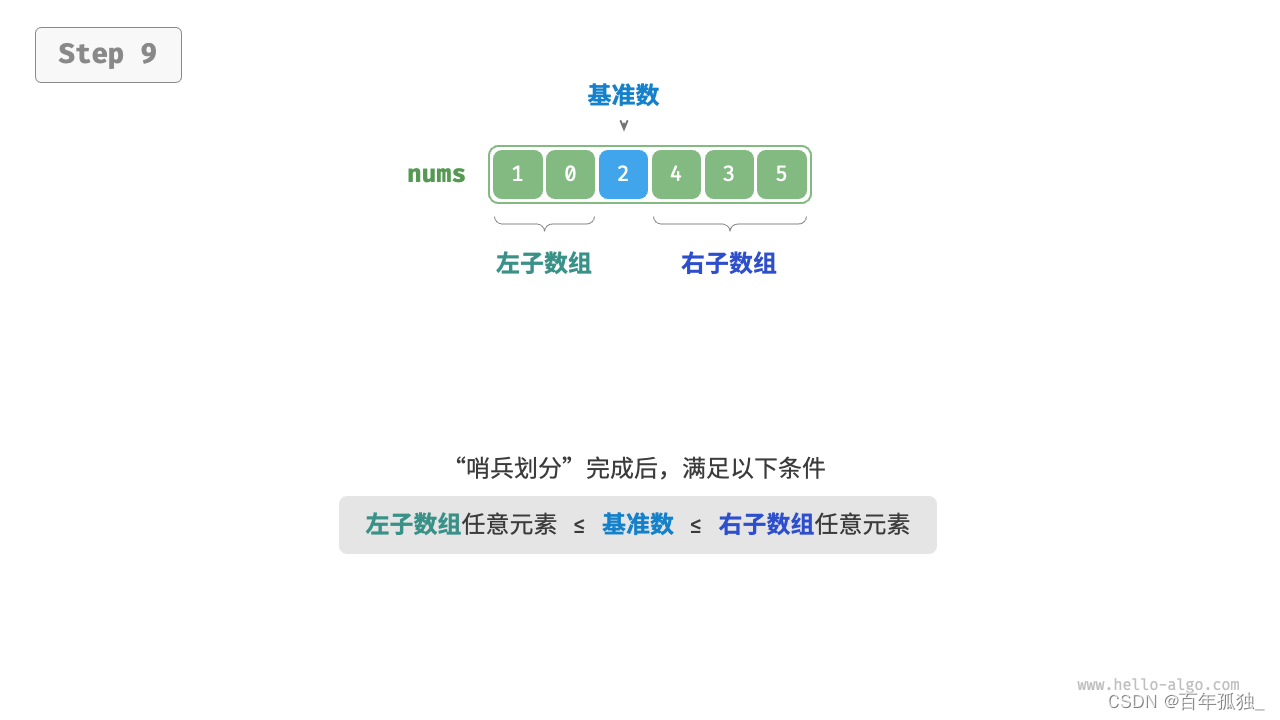
int partition(vector<int>& nums, int left, int right) {// 以 nums[left] 为基准数int i = left, j = right;while (i < j) {while (i < j && nums[j] >= nums[left])j--; // 从右向左找首个小于基准数的元素while (i < j && nums[i] <= nums[left])i++;          // 从左向右找首个大于基准数的元素swap(nums, i, j); // 交换这两个元素}swap(nums, i, left); // 将基准数交换至两子数组的分界线return i;            // 返回基准数的索引
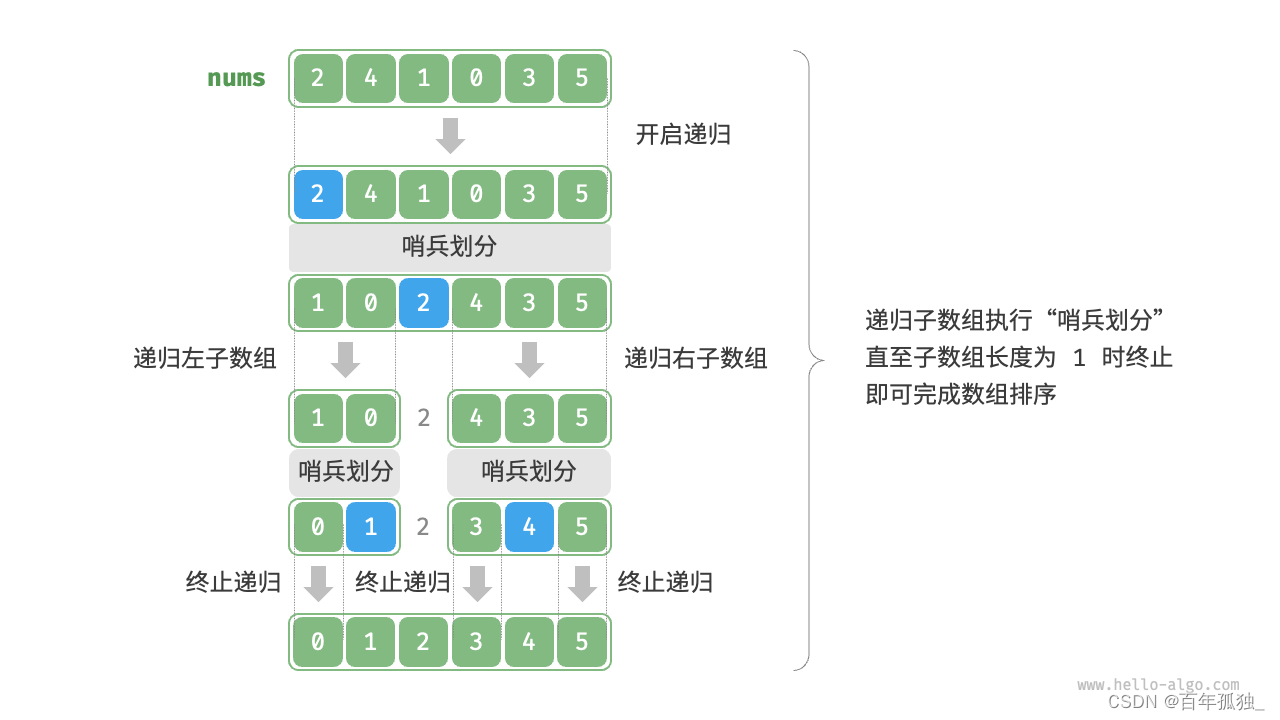
}/* 快速排序 */
void quickSort(vector<int>& nums, int left, int right) {// 子数组长度为 1 时终止递归if (left >= right)return;// 哨兵划分int pivot = partition(nums, left, right);// 递归左子数组、右子数组quickSort(nums, left, pivot - 1);quickSort(nums, pivot + 1, right);
}

堆排序

参考：数据结构之堆火烨烨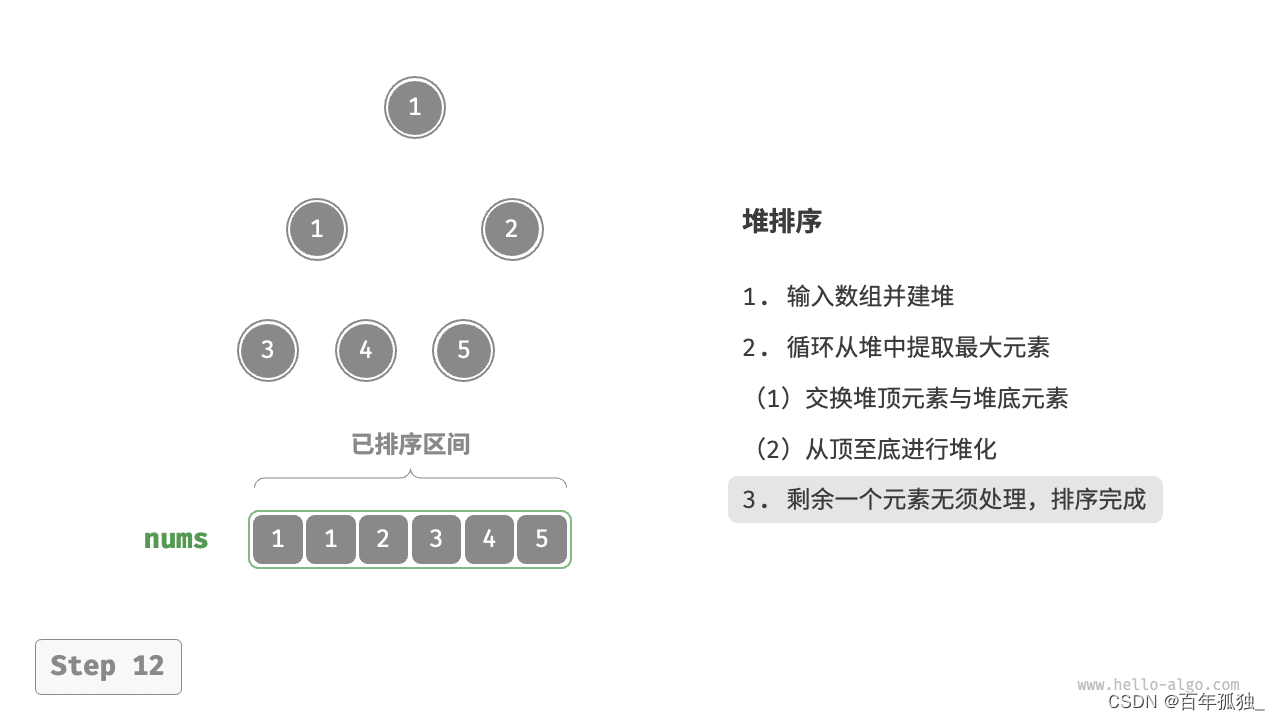在这里插入图片描述

#include <vector>
#include <iostream>
#include <algorithm> // 引入 swap 函数using namespace std;// 向下调整堆
void siftDown(vector<int>& nums, int n, int i) {while (true) {int l = 2 * i + 1;int r = 2 * i + 2;int ma = i;if (l < n && nums[l] > nums[ma])ma = l;if (r < n && nums[r] > nums[ma])ma = r;if (ma == i) {break;}swap(nums[i], nums[ma]);i = ma;}
}/* 堆排序 */
void heapSort(vector<int>& nums) {int n = nums.size();// 建堆操作for (int i = n / 2 - 1; i >= 0; --i) {siftDown(nums, n, i);}// 提取最大元素并重新建堆for (int i = n - 1; i > 0; --i) {swap(nums[0], nums[i]);siftDown(nums, i, 0);}
}int main() {vector<int> nums = { 10, 30, 40, 20, 100 };cout << "Before sorting: ";for (int num : nums) {cout << num << " ";}cout << endl;heapSort(nums);cout << "After sorting: ";for (int num : nums) {cout << num << " ";}cout << endl;return 0;
}

桶排序

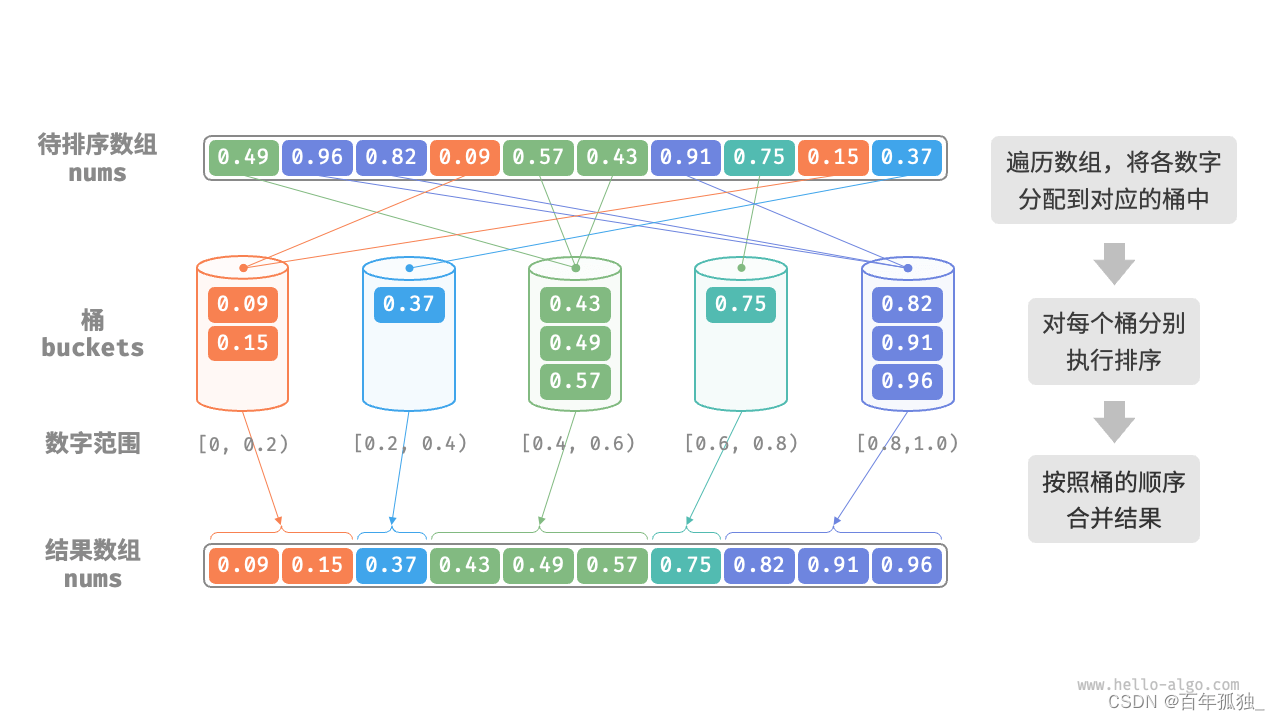
在这里插入图片描述

/* 桶排序 */
void bucketSort(vector<float> &nums) {// 初始化 k = n/2 个桶，预期向每个桶分配 2 个元素int k = nums.size() / 2;vector<vector<float>> buckets(k);// 1. 将数组元素分配到各个桶中for (float num : nums) {// 输入数据范围为 [0, 1)，使用 num * k 映射到索引范围 [0, k-1]int i = num * k;// 将 num 添加进桶 bucket_idxbuckets[i].push_back(num);}// 2. 对各个桶执行排序for (vector<float> &bucket : buckets) {// 使用内置排序函数，也可以替换成其他排序算法sort(bucket.begin(), bucket.end());}// 3. 遍历桶合并结果int i = 0;for (vector<float> &bucket : buckets) {for (float num : bucket) {nums[i++] = num;}}
}

难点：归并排序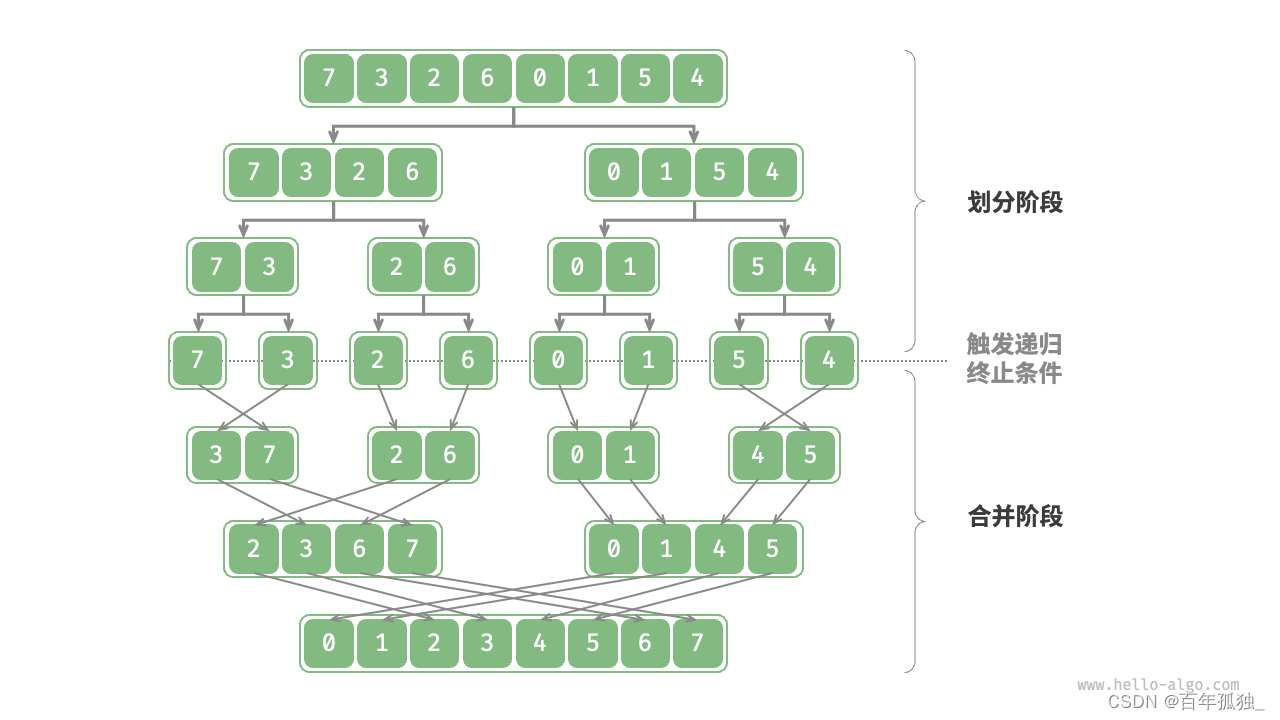

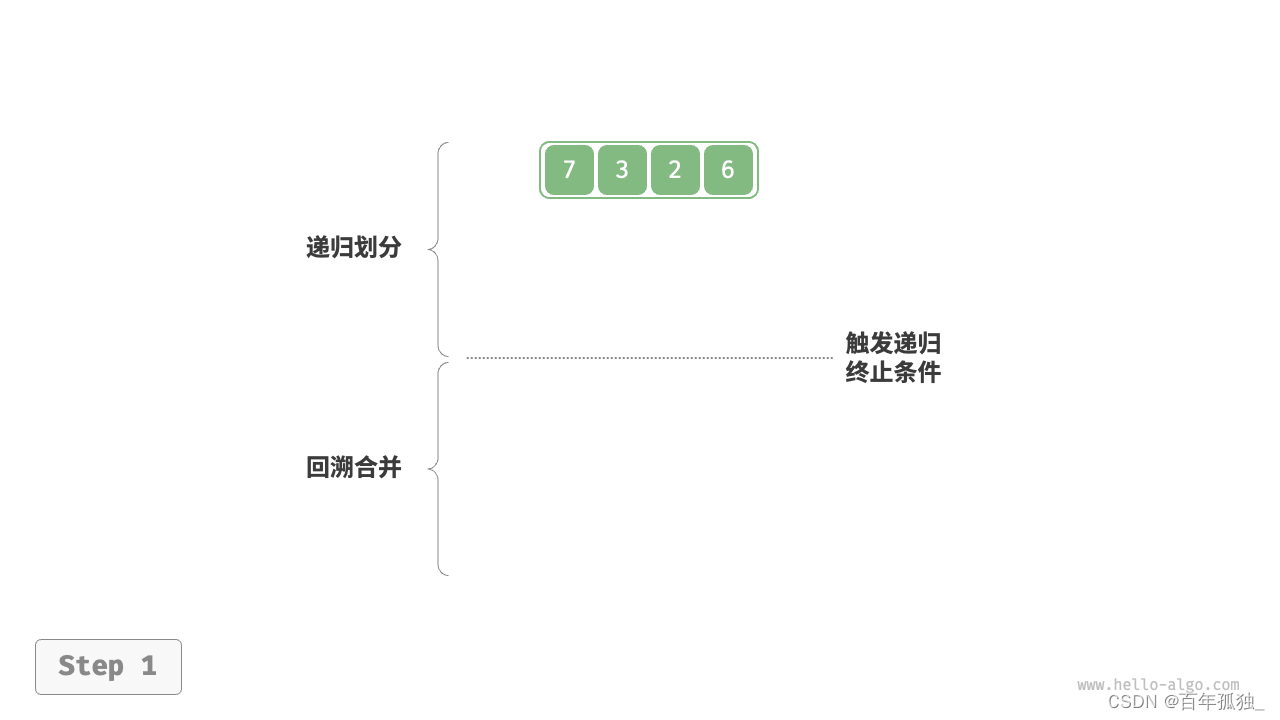
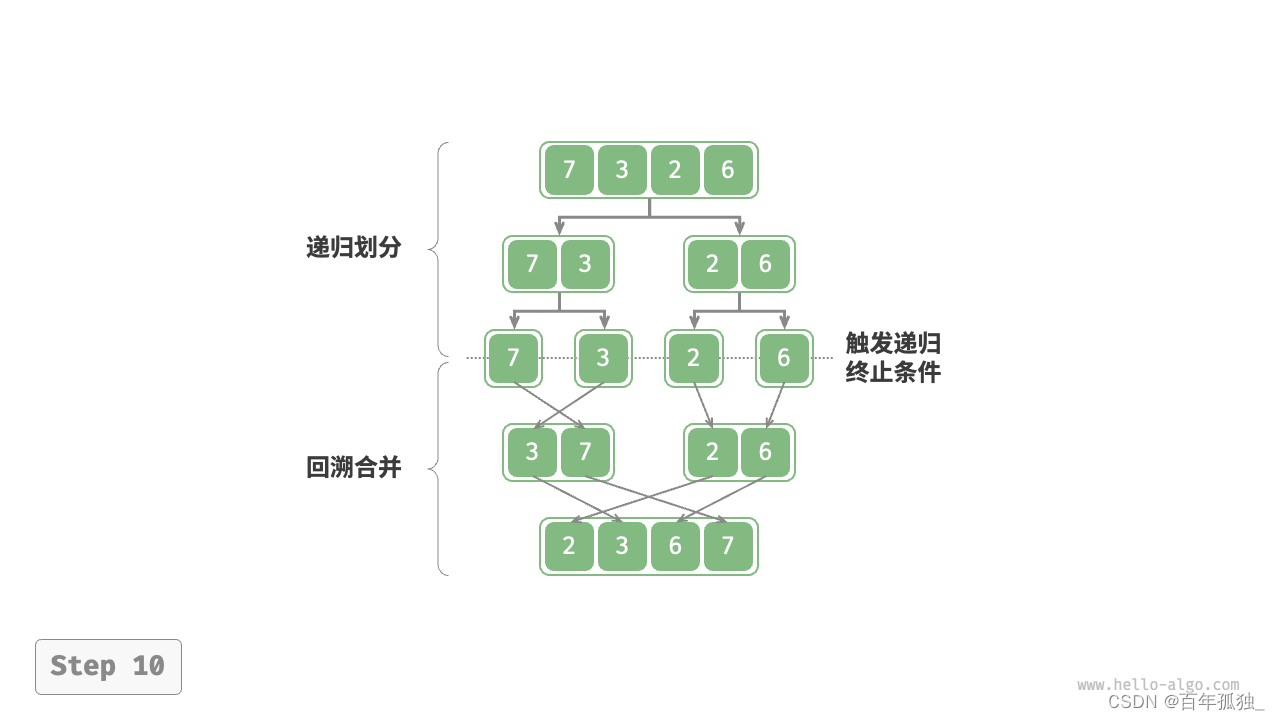
实现

/* 合并左子数组和右子数组 */
void merge(vector<int> &nums, int left, int mid, int right) {// 左子数组区间为 [left, mid], 右子数组区间为 [mid+1, right]// 创建一个临时数组 tmp ，用于存放合并后的结果vector<int> tmp(right - left + 1);// 初始化左子数组和右子数组的起始索引int i = left, j = mid + 1, k = 0;// 当左右子数组都还有元素时，进行比较并将较小的元素复制到临时数组中while (i <= mid && j <= right) {if (nums[i] <= nums[j])tmp[k++] = nums[i++];elsetmp[k++] = nums[j++];}// 将左子数组和右子数组的剩余元素复制到临时数组中while (i <= mid) {tmp[k++] = nums[i++];}while (j <= right) {tmp[k++] = nums[j++];}// 将临时数组 tmp 中的元素复制回原数组 nums 的对应区间for (k = 0; k < tmp.size(); k++) {nums[left + k] = tmp[k];}
}/* 归并排序 */
void mergeSort(vector<int> &nums, int left, int right) {// 终止条件if (left >= right)return; // 当子数组长度为 1 时终止递归// 划分阶段int mid = (left + right) / 2;    // 计算中点mergeSort(nums, left, mid);      // 递归左子数组mergeSort(nums, mid + 1, right); // 递归右子数组// 合并阶段merge(nums, left, mid, right);
}