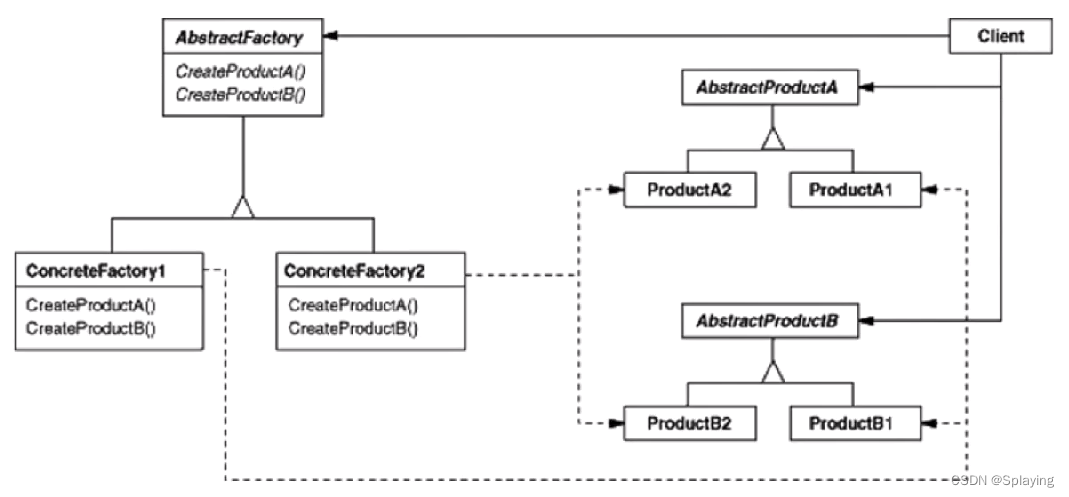
文章目录
- 1、求根节点到叶节点数字之和
- 2、二叉树剪枝
- 3、验证二叉搜索树
- 4、二叉搜索树中第K小的元素
- 5、二叉树的所有路径
1、求根节点到叶节点数字之和
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。

class Solution {
public:int dfs(TreeNode* root,int presum){presum=presum*10+root->val;if(root->left==nullptr&&root->right==nullptr)return presum;int ret=0;if(root->left) ret+=dfs(root->left,presum);if(root->right) ret+=dfs(root->right,presum);return ret;}int sumNumbers(TreeNode* root) {return dfs(root,0);}
};
2、二叉树剪枝
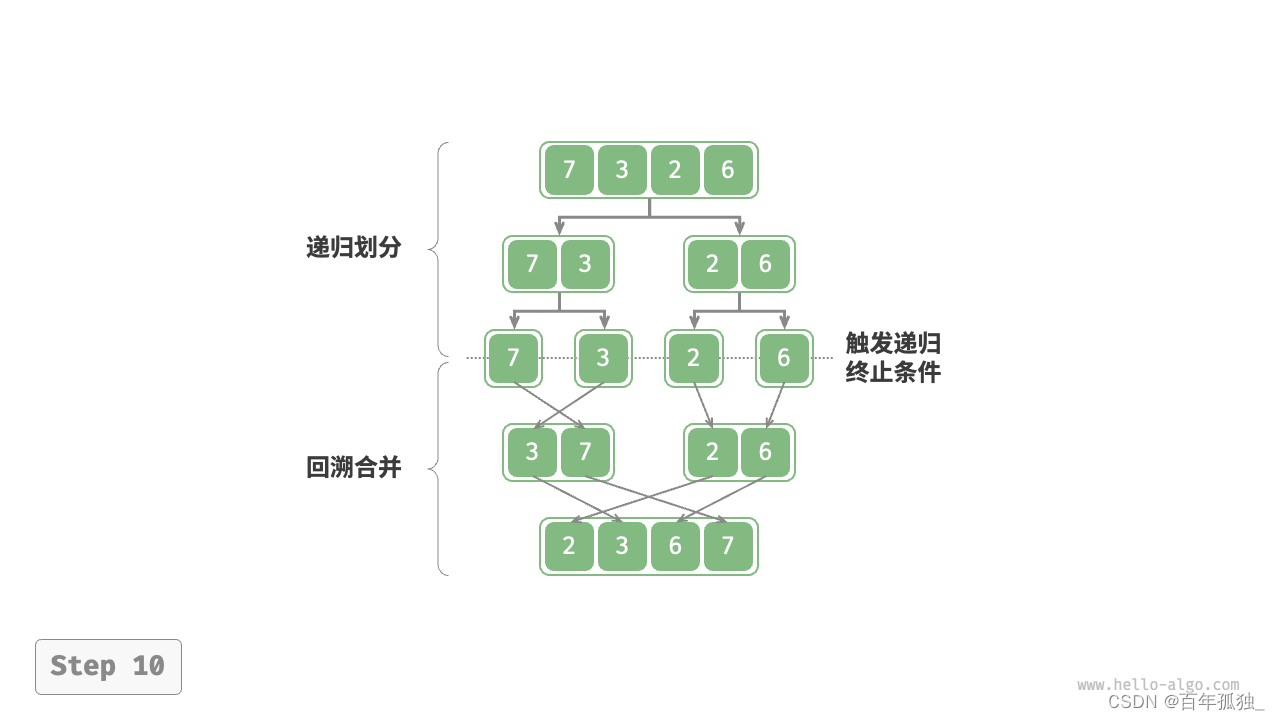
给你二叉树的根结点 root ,此外树的每个结点的值要么是 0 ,要么是 1 。
返回移除了所有不包含 1 的子树的原二叉树。
节点 node 的子树为 node 本身加上所有 node 的后代。
class Solution {
public:TreeNode* pruneTree(TreeNode* root) {if(root==nullptr)return nullptr;root->left=pruneTree(root->left);root->right=pruneTree(root->right);if(root->left==nullptr&&root->right==nullptr&&root->val==0){delete root;//可加可不加return nullptr;}return root;}
};
3、验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树
只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

class Solution {
public:long flag=LONG_MIN;bool isValidBST(TreeNode* root) {if(root==nullptr)return true;bool left=isValidBST(root->left);if(left==false) return false;//剪枝,作用为了提高效率bool cur=false;if(root->val>flag){ cur=true;flag=root->val;}if(cur==false) return false;//剪枝bool right=isValidBST(root->right);return left&&right&&cur;}
};
4、二叉搜索树中第K小的元素
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)

class Solution {
public:int count=0;int ret=0;void dfs(TreeNode* root,int k){if(root==nullptr||count==k)//count==0是剪枝return ;dfs(root->left,k);count++;if(count==k)ret=root->val;dfs(root->right,k);}int kthSmallest(TreeNode* root, int k) {dfs(root,k);return ret;}
};
5、二叉树的所有路径
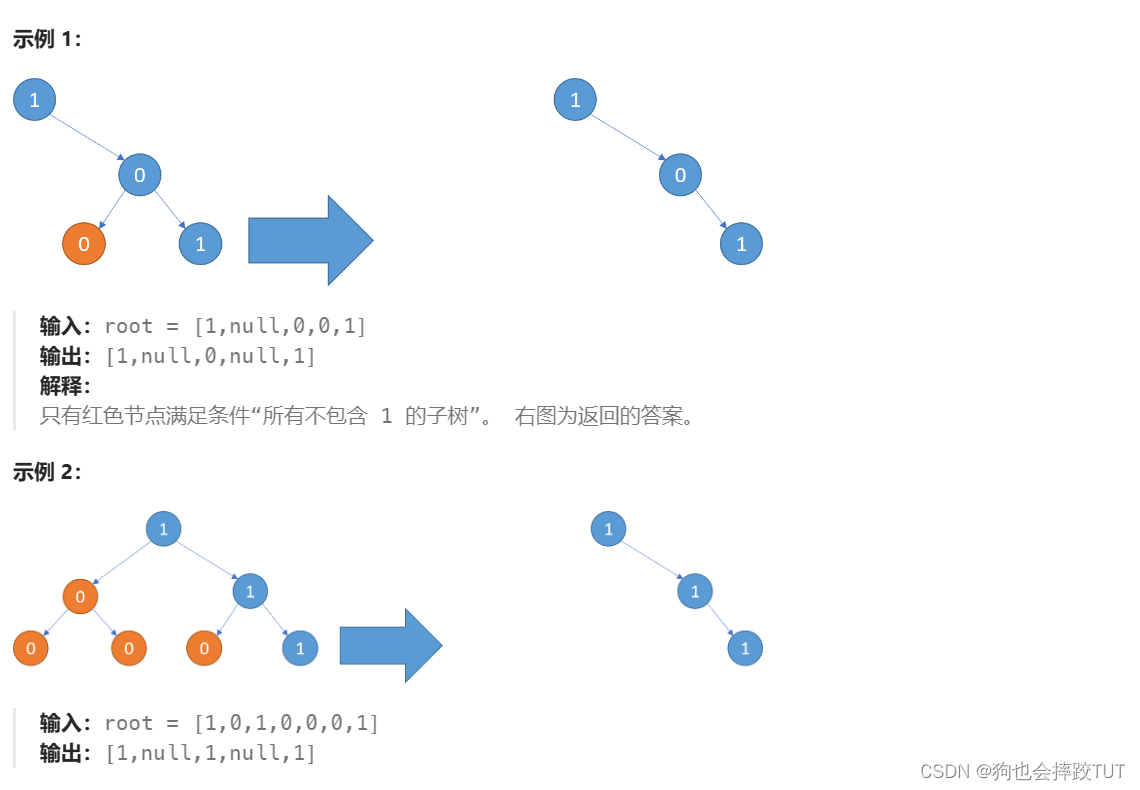
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
class Solution {
public:vector<string> dummy;void dfs(TreeNode* root,string str){str+=to_string(root->val);if(root->left==nullptr&&root->right==nullptr){dummy.push_back(str);return;}str+="->";if(root->left) dfs(root->left,str);//dfs(root->left,str);之前的操作是没有判断,不能只if(root->right) dfs(root->right,str);//判断root->left==nullptr&&root->right==nullptr,//还要想着单子树的问题,已经好几次了}vector<string> binaryTreePaths(TreeNode* root) {dfs(root,"");return dummy;}
};

![天池医疗AI大赛[第一季] Rank5解决方案](https://img-blog.csdnimg.cn/direct/8e11a5b551114391a483e1a039bc5603.png)