【算法刷题】八大排序算法总结（冒泡、选择、插入、二分插入、归并、快速、希尔、堆排序）

在这里插入图片描述

文章目录

  • 八大排序算法总结
  • 1.冒泡排序
  • 2.选择排序
  • 3.插入排序
  • 4.二分插入排序
  • 5.归并排序
  • 6.快速排序
  • 7.希尔排序
  • 8.堆排序

八大排序算法总结

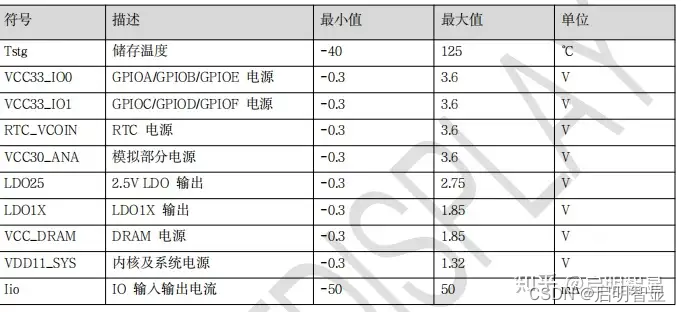
排序排序方法平均情况最好情况最坏情况空间稳定性
1冒泡排序O(n2)O(n)O(n2)O(1)稳定
2选择排序O(n2)O(n2)O(n2)O(1)不稳定
3插入排序O(n2)O(n)O(n2)O(1)稳定
4二分插入排序O(n2)O(n)O(n2)O(1)稳定
5归并排序O(nlogn)O(nlogn)O(nlogn)O(n)稳定
6快速排序O(nlogn)O(nlogn)O(n2)O(logn)~O(n)不稳定
7希尔排序O(nlogn) ~ O(n2)O(n1.3)O(n2)O(1)不稳定
8堆排序O(nlogn)O(nlogn)O(nlogn)O(1)不稳定

1.冒泡排序

  1. 核心思想： 通过相邻元素的比较和交换来将最大（或最小）的元素逐渐“冒泡”到数组的一端

    动图

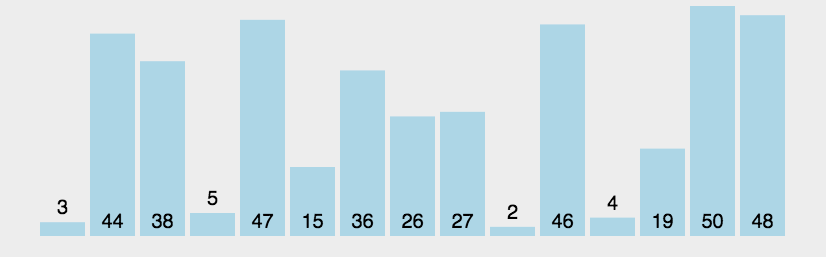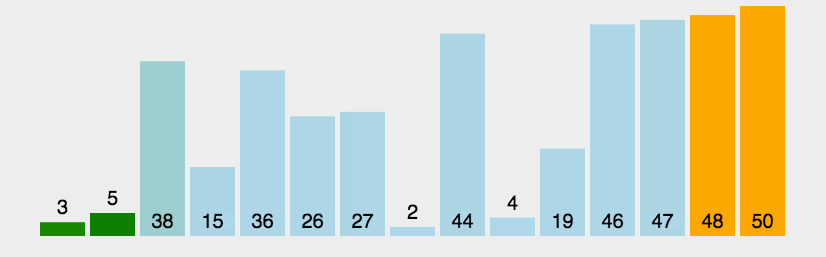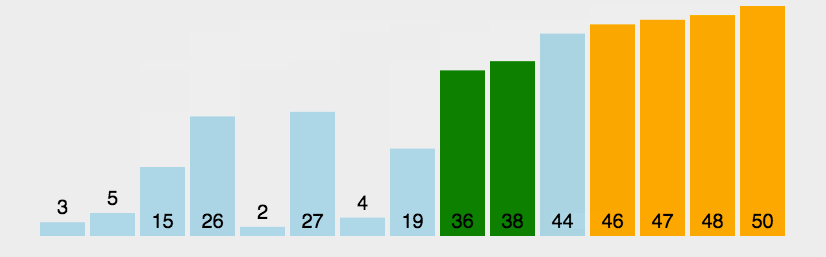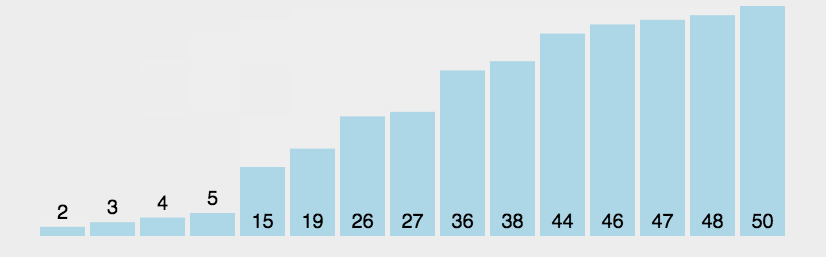
  2. 具体步骤：

    1. 从数组的第一个元素开始，依次比较相邻的两个元素。
    2. 如果前一个元素大于后一个元素，则交换它们的位置，使得较大的元素“冒泡”到后面。
    3. 继续进行相邻元素的比较和交换，直到数组的末尾。
    4. 重复执行上述步骤，每次都会将当前未排序部分的最大元素“冒泡”到数组的末尾。
    5. 重复执行上述步骤，直到整个数组排序完成。

  3. 实现代码：

    public static void bubbleSort(int[] arr) {int temp = 0;for (int i = arr.length - 1; i > 0; i--) { 	// 每次需要排序的长度for (int j = 0; j < i; j++) { 			// 从第一个元素到第i个元素if (arr[j] > arr[j + 1]) {			// 确保较大的元素排到后面temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}
}

  4. 时间和空间复杂度：

    • 平均情况：O(n2)
    • 最好情况：O(n)
    • 最坏情况：O(n2)
    • 空间复杂度：O(1)
    • 稳定性：稳定

  5. 优化： 增加标记符swap，用于确定当前一轮冒泡是否有元素进行交换，若没有则跳出循环，表示数组已经有序了

    public static void bubbleSort(int[] arr) {int temp = 0;boolean swap;for (int i = arr.length - 1; i > 0; i--) { // 每次需要排序的长度swap=false;for (int j = 0; j < i; j++) { // 从第一个元素到第i个元素if (arr[j] > arr[j + 1]) {temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;swap=true;}}//loop jif (swap==false){			//前面的一轮循环没有进行交换，数组已经有序break;}}//loop i
}// method bubbleSort

2.选择排序

  1. 核心思想： 在未排序部分的数据中选择最小（或最大）的元素，然后将其放置到已排序部分的末尾

  2. 具体步骤：

    1. 遍历数组，将第一个元素作为当前最小（或最大）元素。
    2. 在未排序部分的剩余元素中，找到最小（或最大）的元素，并记录其位置。
    3. 将找到的最小（或最大）元素与未排序部分的第一个元素交换位置，将其放置到已排序部分的末尾。
    4. 重复执行上述步骤，每次都会将当前未排序部分的最小（或最大）元素放置到已排序部分的末尾。
    5. 这样，经过n-1轮的遍历和交换，整个数组就会按照升序（或降序）排列。

  3. 实现代码：

    public static void selectionSort(int[] arr) {int temp, min = 0;for (int i = 0; i < arr.length - 1; i++) {min = i;// 循环查找最小值for (int j = i + 1; j < arr.length; j++) {if (arr[min] > arr[j]) {min = j;}}if (min != i) {temp = arr[i];arr[i] = arr[min];arr[min] = temp;}}
}

  4. 时间和空间复杂度：

    • 平均情况：O(n2)
    • 最好情况：O(n2)
    • 最坏情况：O(n2)
    • 空间复杂度：O(1)
    • 稳定性：不稳定

  5. 关于稳定性的探讨：

    • 稳定性：在排序过程中，相等元素的相对顺序是否会被改变。如果排序算法能够保持相等元素的相对顺序不变，则称其为稳定的排序算法；反之，则称其为不稳定的排序算法

    • 冒泡排序（升序）：当相邻元素进行比较并需要交换位置时，只有当后面的元素小于前面的元素才会进行交换。因此，对于相等的元素，即使它们相邻，它们的相对顺序也不会被改变，从而保持了排序的稳定性

    • 选择排序：每次选择最小的元素并放置到已排序部分的末尾。在寻找最小（或最大）元素的过程中，可能会导致相等元素的相对顺序发生改变。例如，在一组相等的元素中，由于选择排序每次只选择一个最小（或最大）元素，所以在选择的过程中可能会交换这些相等元素的位置，从而导致排序的不稳定性

    • 举例：假设我们有以下一组待排序的元素：

      [5①, 2, 7, 5②, 1]

      • 冒泡排序：比较相邻的元素，并根据需要交换它们的位置。当遇到相等元素时，只有在后面的元素小于前面的元素时才会进行交换。

        第一轮冒泡排序：[2, 5①, 5②, 1, 7]
第二轮冒泡排序：[2, 5, 1, 5, 7]
第三轮冒泡排序：[2, 1, 5, 5, 7]
第四轮冒泡排序：[1, 2, 5, 5, 7]

      • 选择排序：

        第一轮选择排序：[1, 2, 7, 5②, 5①]（选择1） （两个相等的5的位置发生变化，不稳定!!!）
第二轮选择排序：[1, 2, 5, 5, 7]（选择2）
第三轮选择排序：[1, 2, 5, 5, 7]（选择5）
第四轮选择排序：[1, 2, 5, 5, 7]（选择5）
第五轮选择排序：[1, 2, 5, 5, 7]（选择7）

3.插入排序

  1. 核心思想： 将待排序的元素逐个插入到已排序部分的正确位置

    动图

  2. 具体步骤：

    1. 将数组分为已排序部分和未排序部分。一开始，已排序部分只包含第一个元素，即数组的第一个元素被认为是已排序的。
    2. 从未排序部分取出一个元素，将其插入到已排序部分的正确位置。为了找到正确的位置，可以从已排序部分的末尾开始，依次向前比较已排序元素，直到找到小于等于该元素的位置。
    3. 将该元素插入到找到的位置，并将已排序部分中的元素向后移动，为新元素腾出位置。
    4. 重复步骤2和步骤3，直到未排序部分为空。
    5. 最终，已排序部分即为排序好的数组。

  3. 实现代码：

    public static void insertionSort(int[] arr) {int n = arr.length;for (int i = 1; i < n; i++) {		//从第二个元素开始，第一个元素默认有序int key = arr[i];				//保存当前元素 keyint j = i - 1;//找到合适的位置while (j >= 0 && arr[j] > key) {//发现已排序元素比 key 大，则将该元素向后移动一位，直到找到 key 的正确位置arr[j + 1] = arr[j];j = j - 1;					//往后移}	arr[j + 1] = key;1				//找到 key 保存的位置}
}

    待排序数组：[5, 2, 4, 6, 1, 3]
1：[2, 5, 4, 6, 1, 3]
2：[2, 4, 5, 6, 1, 3]
3：[1, 2, 4, 5, 6, 3]
4：[1, 2, 3, 4, 5, 6]

  4. 时间和空间复杂度：

    • 平均情况：O(n2)
    • 最好情况：O(n)
    • 最坏情况：O(n2)
    • 空间复杂度：O(1)
    • 稳定性：稳定

4.二分插入排序

  1. 核心思想：利用二分查找来确定待插入元素在已排序部分中的位置，以减少比较次数

  2. 实现步骤：

    1. 初始状态：将数组的第一个元素视为已排序部分，其余元素视为待排序部分。
    2. 插入过程：从第二个元素开始遍历待排序部分，对于每个元素，使用二分查找确定其在已排序部分中的插入位置。
    3. 二分查找：在已排序部分中，使用二分查找找到第一个大于待插入元素的位置，这个位置及之后的元素都需要向后移动一个位置来腾出空间。
    4. 插入操作：将待插入元素插入到找到的位置，完成一轮插入操作。
    5. 重复步骤2~4，直到待排序部分中的所有元素都被插入到已排序部分中，整个数组就被排序完成了。

  3. 实现代码：

    public static void binaryInsertionSort(int[] arr) {int n = arr.length;for (int i = 1; i < n; i++) {int key = arr[i];int left = 0;int right = i - 1;// 二分查找确定插入位置int insertIndex = binarySearch(arr, left, right, key);// 将大于 key 的元素向后移动一位for (int j = i - 1; j >= insertIndex; j--) {arr[j + 1] = arr[j];}// 插入 keyarr[insertIndex] = key;}
}// 二分查找
private static int binarySearch(int[] arr, int left, int right, int key) {while (left <= right) {int mid = left + (right - left) / 2;if (arr[mid] == key) {return mid; // key 在已排序部分的位置} else if (arr[mid] < key) {left = mid + 1;} else {right = mid - 1;}}return left; // 返回待插入位置
}

  4. 时间和空间复杂度：

    • 平均情况：O(n2)
    • 最好情况：O(n)
    • 最坏情况：O(n2)
    • 空间复杂度：O(1)
    • 稳定性：稳定

5.归并排序

  1. 核心思想： 采用分治法，将已有序的子序列合并，得到完全有序的序列；

  2. 步骤：

    1. 分解（Divide）：将原始数组分解为较小的子数组，直到每个子数组只有一个元素为止。这可以通过递归的方式实现，将数组不断二分直到每个子数组的长度为1。
    2. 解决（Conquer）：对每个子数组进行排序。对于只有一个元素的子数组来说，可以认为它们已经是有序的。
    3. 合并（Merge）：合并相邻的子数组，形成一个更大的有序数组。合并过程中，需要按照大小顺序逐个比较两个子数组中的元素，并将较小（或较大）的元素依次放入一个临时数组中，直到合并完成。
    4. 递归合并（Recursively Merge）：重复以上步骤，直到所有子数组都被合并成一个大的有序数组为止。

    动图

  3. 实现代码：

    public static void mergeSort(int[] arr){int[] temp =new int[arr.length];internalMergeSort(arr, temp, 0, arr.length-1);
}
private static void internalMergeSort(int[] arr, int[] temp, int left, int right){//当left==right的时，已经不需要再划分了if (left<right){int middle = (left+right)/2;internalMergeSort(arr, temp, left, middle);          //左子数组internalMergeSort(arr, temp, middle+1, right);       //右子数组mergeSortedArray(arr, temp, left, middle, right);    //合并两个子数组}
}
// 合并两个有序子序列
private static void mergeSortedArray(int arr[], int temp[], int left, int middle, int right){int i=left;      int j=middle+1;int k=0;while (i<=middle && j<=right){temp[k++] = arr[i] <= arr[j] ? arr[i++] : arr[j++];}while (i <=middle){temp[k++] = arr[i++];}while ( j<=right){temp[k++] = arr[j++];}//把数据复制回原数组for (i=0; i<k; ++i){arr[left+i] = temp[i];}
}

  4. 时间和空间复杂度：

    • 平均情况：O(nlogn)
    • 最好情况：O(nlogn)
    • 最坏情况：O(nlogn)
    • 空间复杂度：O(n)
    • 稳定性：稳定

  5. 适用场景： 归并排序在数据量比较大的时候也有较为出色的表现（效率上），但是，其空间复杂度O(n)使得在数据量特别大的时候（例如，1千万数据）几乎不可接受。而且，考虑到有的机器内存本身就比较小，因此，采用归并排序一定要注意。

6.快速排序

  1. 核心思想： 通过选取基准元素，将数组划分为两个子数组，并对子数组递归排序，实现整个数组的快速排序

  2. 实现步骤：

    1. 从数列中挑出一个元素，称为 “基准”（pivot），
    2. 重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（相同的数可以到任何一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
    3. 递归地（recursively）把小于基准值元素的子数列和大于基准值元素的子数列排序。

  3. 实现代码：

    public static void quickSort(int[] arr){qsort(arr, 0, arr.length-1);
}private static void qsort(int[] arr, int low, int high){if (low >= high)return;int pivot = partition(arr, low, high);        //将数组分为两部分qsort(arr, low, pivot-1);                   //递归排序左子数组qsort(arr, pivot+1, high);                  //递归排序右子数组
}private static int partition(int[] arr, int low, int high){int pivot = arr[low];     //基准while (low < high){while (low < high && arr[high] >= pivot){--high;} arr[low]=arr[high];             //比基准小的元素会被移动到基准的左边while (low < high && arr[low] <= pivot){++low;}arr[high] = arr[low];           //比基准大的元素会被移动到基准的右边}//扫描完成，基准到位arr[low] = pivot;//返回的是基准的位置return low;
}

  4. 举例：

    初始：[7, 2, 1, 6, 8, 5, 3, 4]	# 7为基准第一：[4, 2, 1, 6, 8, 5, 3, 4] # 4移到左边[4, 2, 1, 6, 8, 5, 3, 8] # 8移到右边[4, 2, 1, 6, 3, 5, 3, 8] # 3移到左边[4, 2, 1, 6, 3, 5, 7, 8] # 基准7插入到low位置划分为两个数组：[4, 2, 1, 6, 3, 5]和[8]
第二： [4, 2, 1, 6, 3, 5] # 以4为基准[3, 2, 1, 6, 3, 5] # 3移到左边[3, 2, 1, 6, 6, 5] # 6移到右边[3, 2, 1, 4, 6, 5] # 基准4插入到low位置以此类推......

  5. 时间和空间复杂度：

    • 平均情况：O(nlogn)
    • 最好情况：O(nlogn)
    • 最坏情况：O(n2)
    • 空间复杂度：O(logn)~O(n)
    • 稳定性：不稳定

7.希尔排序

  • 明天总结

8.堆排序

  • 明天总结

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/303209.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

XUbuntu22.04之Typora添加水印并输出pdf文件(二百二十七)

XUbuntu22.04之Typora添加水印并输出pdf文件(二百二十七)

简介： CSDN博客专家，专注Android/Linux系统，分享多mic语音方案、音视频、编解码等技术，与大家一起成长！ 优质专栏：Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏：多媒体系统工程师系列【原创干货持续更新中……】🚀 优质视频课程：AAOS车载系统+AOSP…
阅读更多...
30个Python操作小技巧

30个Python操作小技巧

前言 1、列表推导 列表的元素可以在一行中进行方便的循环。 numbers [1, 2, 3, 4, 5, 6, 7, 8] even_numbers [number for number in numbers if number % 2 0] print(even_numbers)输出&#xff1a; 在这里插入代码片[1,3,5,7] 同时&#xff0c;也可以用在字典上。 d…
阅读更多...
前端入门：极简登录网页的制作（未使用JavaScript制作互动逻辑）

前端入门：极简登录网页的制作（未使用JavaScript制作互动逻辑）

必备工具&#xff1a;vscode Visual Studio Code - Code Editing. Redefined 目录 前言 准备 HTML源文件的编写&#xff08;构建&#xff09; head部分 body部分 网页背景设置 网页主体构建 CSS源文件的编写&#xff08;设计&#xff09; 结果展示 前言 博主稍稍自…
阅读更多...
计算机视觉——引导APSF和梯度自适应卷积增强夜间雾霾图像的可见性算法与模型部署（C++/python）

计算机视觉——引导APSF和梯度自适应卷积增强夜间雾霾图像的可见性算法与模型部署（C++/python）

摘要 在夜间雾霾场景中&#xff0c;可见性经常受到低光照、强烈光晕、光散射以及多色光源等多种因素的影响而降低。现有的夜间除雾方法常常难以处理光晕或低光照条件&#xff0c;导致视觉效果过暗或光晕效应无法被有效抑制。本文通过抑制光晕和增强低光区域来提升单张夜间雾霾…
阅读更多...
LINUX系统触摸工业显示器芯片应用方案--Model4（简称M4芯片）

LINUX系统触摸工业显示器芯片应用方案--Model4（简称M4芯片）

背景介绍&#xff1a; 触摸工业显示器传统的还是以WINDOWS为主&#xff0c;但近年来&#xff0c;安卓紧随其后&#xff0c;但一直市场应用情况不够理想&#xff0c;反而是LINUX系统的触摸工业显示器大受追捧呢&#xff1f; 触摸工业显示器传统是以Windows系统为主&#xff0c…
阅读更多...
计算机视觉异常检测——PatchCore面向全召回率的工业异常检测

计算机视觉异常检测——PatchCore面向全召回率的工业异常检测

1. 概述 异常检测问题在工业图像数据分析中扮演着至关重要的角色&#xff0c;其目的是从大量正常数据中识别出异常行为或模式。这一任务的挑战在于&#xff0c;正常数据的样本相对容易获取&#xff0c;而异常情况却因其稀有性和多样性而难以收集。为了解决这一问题&#xff0c…
阅读更多...
Django之五种中间件定义类型—process_request、process_view、process_response.......

Django之五种中间件定义类型—process_request、process_view、process_response.......

目录 1. 前言 2. 基础中间件 3. 如何自定义中间件 4. 五种自定义中间件类型 4.1 process_request 4.2 process_view 4.3 process_response 4.4 process_exception 4.5 process_template_response 5. 最后 1. 前言 哈喽&#xff0c;大家好&#xff0c;我是小K,今天咋们…
阅读更多...
51单片机学习笔记15 LCD12864（带字库）显示屏使用

51单片机学习笔记15 LCD12864（带字库）显示屏使用

51单片机学习笔记15 LCD12864&#xff08;带字库&#xff09;显示屏使用 一、LCD12864简介二、管脚定义三、命令1. 功能能设定2. 清屏指令&#xff08;0x01&#xff09;3. 地址归位4. 进入设定点5. 显示状态开关6. 设定CGRAM地址7. 设定DDRAM地址8. 写资料到RAM9. 读出RAM 四、…
阅读更多...
【目标检测】-入门知识

【目标检测】-入门知识

1、回归与分类问题 回归问题是指给定输入变量（特征）和一个连续的输出变量（标签），建立一个函数来预测输出变量的值。换句话说，回归问题的目标是预测一个连续的输出值，例如预测房价、股票价格、销售额等。回归问题通常使用回归分析技术，例如线性回归、多项式回归、决策树…
阅读更多...
嵌入式学习48-单片机1

嵌入式学习48-单片机1

51单片机—————8位单片机 裸机驱动 无系统 linux驱动 有系统 驱动-----反映硬件变化 MCU 微控器 MPU CPU GPU 图像处理 IDE 集成开发环境 peripheral 外设 SOC&#xff1a; system on chip P0&#xff1a;8bit——8个引脚 …
阅读更多...
【架构师】-- 浅淡架构的分类

【架构师】-- 浅淡架构的分类

什么是架构&#xff1f; 说到架构&#xff0c;这个概念没有很清晰的范围划分&#xff0c;也没有一个标准的定义&#xff0c;每个人的理解可能都不一样。 架构在百度百科中是这样定义的&#xff1a;架构&#xff0c;又名软件架构&#xff0c;是有关软件整体结构与组件的抽象描…
阅读更多...
vue快速入门（十二）v-key索引标志

vue快速入门（十二）v-key索引标志

注释很详细&#xff0c;直接上代码 上一篇 新增内容 v-key的使用场景数组筛选器的使用 源码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, i…
阅读更多...
(源码+部署+讲解)基于Spring Boot + Vue编程学习平台的设计与实现

(源码+部署+讲解)基于Spring Boot + Vue编程学习平台的设计与实现

前言 &#x1f497;博主介绍&#xff1a;✌专注于Java、小程序技术领域和毕业项目实战✌&#x1f497; &#x1f447;&#x1f3fb; 精彩专栏 推荐订阅&#x1f447;&#x1f3fb; 2024年Java精品实战案例《100套》 &#x1f345;文末获取源码联系&#x1f345; &#x1f31f;…
阅读更多...
基于PSO优化的CNN-GRU-Attention的时间序列回归预测matlab仿真

基于PSO优化的CNN-GRU-Attention的时间序列回归预测matlab仿真

目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 4.1卷积神经网络&#xff08;CNN&#xff09;在时间序列中的应用 4.2 GRU网络 4.3 注意力机制&#xff08;Attention&#xff09; 5.算法完整程序工程 1.算法运行效果图预览 优化前 优化…
阅读更多...
番茄 abogus rpc调用

番茄 abogus rpc调用

声明: 本文章中所有内容仅供学习交流使用&#xff0c;不用于其他任何目的&#xff0c;抓包内容、敏感网址、数据接口等均已做脱敏处理&#xff0c;严禁用于商业用途和非法用途&#xff0c;否则由此产生的一切后果均与作者无关&#xff01;wx a15018601872 本文章…
阅读更多...
STM32+ESP8266水墨屏天气时钟:文字取模和图片取模教程

STM32+ESP8266水墨屏天气时钟:文字取模和图片取模教程

项目背景 本次的水墨屏幕项目需要显示一些图片和文字&#xff0c;所以需要对图片和文字进行取模。 取模步骤 1.打开取模软件 2.选择图形模式 3.设置字模选项 注意&#xff1a;本次项目采用的是水墨屏&#xff0c;并且是局部刷新的代码&#xff0c;所以设置字模选项可能有点…
阅读更多...
人工智能——深度学习

人工智能——深度学习

4. 深度学习 4.1. 概念 深度学习是一种机器学习的分支&#xff0c;旨在通过构建和训练多层神经网络模型来实现数据的高级特征表达和复杂模式识别。与传统机器学习算法相比&#xff0c;深度学习具有以下特点&#xff1a; 多层表示学习&#xff1a;深度学习使用深层神经网络&a…
阅读更多...
linux 迁移home目录以及修改conda中pip的目录，修改pip安装路径

linux 迁移home目录以及修改conda中pip的目录，修改pip安装路径

1&#xff09;sudo rsync -av /home/lrf /data/home/lrf 将/home目录下的文件进行复制&#xff08;假设机械硬盘挂载在/data目录下&#xff09;** 2&#xff09;usermod -d /data/home/lrf -m lrf 修改用户$HOME变量** 3&#xff09;vi /etc/passwd 查看对应用户的$HOME变量是…
阅读更多...
环境监测站升级选择ARM网关驱动精准数据采集

环境监测站升级选择ARM网关驱动精准数据采集

物联网技术的深入发展和环保需求的不断攀升&#xff0c;API调用网关在环境监测领域的应用正成为科技创新的重要推手。其中&#xff0c;集成了API调用功能的ARM工控机/网关&#xff0c;以其出色的计算性能、节能特性及高度稳定性&#xff0c;成功搭建起连接物理世界与数字世界的…
阅读更多...
hive管理之ctl方式

hive管理之ctl方式

hive管理之ctl方式 hivehive --service clictl命令行的命令 #清屏 Ctrl L #或者 &#xff01; clear #查看数据仓库中的表 show tabls; #查看数据仓库中的内置函数 show functions;#查看表的结构 desc表名 #查看hdfs上的文件 dfs -ls 目录 #执行操作系统的命令 &#xff01;命令…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023