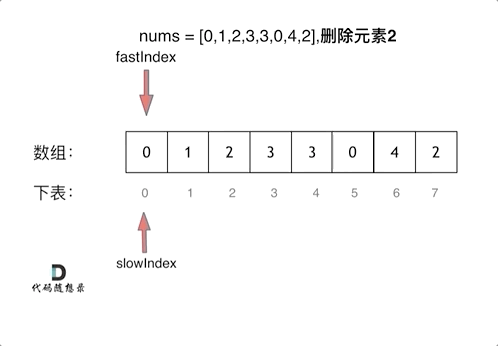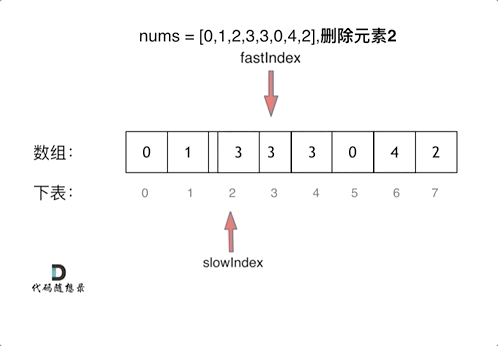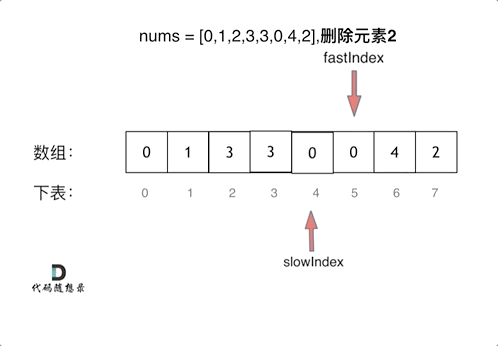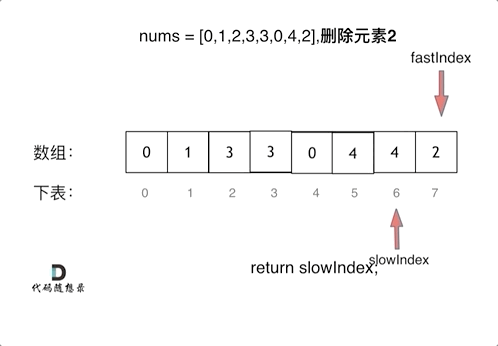
题目
小林在玩一个抽卡游戏,其中有 n种不同的卡牌,编号为 1到 n。
每一次抽卡,她获得第 i种卡牌的概率为 pi。
如果这张卡牌之前已经获得过了,就会转化为一枚硬币。
可以用 k枚硬币交换一张没有获得过的卡。
小林会一直抽卡,直至集齐了所有种类的卡牌为止,求她的期望抽卡次数。
如果你给出的答案与标准答案的绝对误差不超过 10−4,则视为正确。
提示:聪明的小林会把硬币攒在手里,等到通过兑换就可以获得剩余所有卡牌时,一次性兑换并停止抽卡。
输入格式
输入共两行。
第一行包含两个用空格分隔的正整数 n,k,第二行给出 p1,p2,…,pn,用空格分隔。
输出格式
输出共一行,一个实数,即期望抽卡次数。
数据范围
对于 20% 的数据,保证 1≤n,k≤5。 对于另外 20%的数据,保证所有 pi是相等的。 对于 100%的数据,保证
1≤n≤16,1≤k≤5,所有的 pi满足 pi≥110000,且 ∑ni=1pi=1。 注意,本题在官网必须保留
10位小数才能通过(可能是没加SPJ),在本网站无此问题,只要满足你给出的答案与标准答案的绝对误差不超过 10−4,则视为正确。
- 输入样例1:
2 2
0.4 0.6
- 输出样例1:
2.52
样例1解释
共有 2种卡牌,不妨记为 A和 B,获得概率分别为 0.4和 0.6,2枚硬币可以换一张卡牌。下面给出各种可能出现的情况:
第一次抽卡获得 A,第二次抽卡获得 B,抽卡结束,概率为 0.4×0.6=0.24,抽卡次数为 2。
第一次抽卡获得 A,第二次抽卡获得 A,第三次抽卡获得 B,抽卡结束,概率为 0.4×0.4×0.6=0.096,抽卡次数为 3。
第一次抽卡获得 A,第二次抽卡获得 A,第三次抽卡获得 A,用硬币兑换 B,抽卡结束,概率为 0.4×0.4×0.4=0.064,抽卡次数为 3。
第一次抽卡获得 B,第二次抽卡获得 A,抽卡结束,概率为 0.6×0.4=0.24,抽卡次数为 2。
第一次抽卡获得 B,第二次抽卡获得 B,第三次抽卡获得 A,抽卡结束,概率为 0.6×0.6×0.4=0.144,抽卡次数为 3。
第一次抽卡获得 B,第二次抽卡获得 B,第三次抽卡获得 B,用硬币兑换 A,抽卡结束,概率为 0.6×0.6×0.6=0.216,抽卡次数为 3。
因此答案是 0.24×2+0.096×3+0.064×3+0.24×2+0.144×3+0.216×3=2.52。
- 输入样例2:
4 3
0.006 0.1 0.2 0.694
- 输出样例2:
7.3229920752
题解
import java.text.DecimalFormat;
import java.util.*;/*** @author amuya* @create 2024-04-10-19:46*/
public class CollectCards {static int n,m;static int N=16;static int M=1<<N;//硬币不超过80,超过80直接结束static double f[][]=new double[M][N*5+1];static double p[]=new double[N+1];public static void main(String[] args) {Scanner scanner=new Scanner(System.in);n=scanner.nextInt();m=scanner.nextInt();for(int i=1;i<=n;i++){p[i]=scanner.nextDouble();}for(int i=0;i<M;i++) Arrays.fill(f[i],-1);DecimalFormat df=new DecimalFormat("#.##########");String s=df.format(dp(0,0,n));System.out.println(s);}public static double dp(int a,int b,int r){if(f[a][b]>=0) return f[a][b];if(b>=r*m) {f[a][b]=0;return 0;}f[a][b]=0;for(int i=0;i<n;i++){if((a&(1<<i))>0){f[a][b]+=p[i+1]*(dp(a,b+1,r)+1);}else{f[a][b]+=p[i+1]*(dp(a|(1<<i),b,r-1)+1);}}return f[a][b];}
}思路
使用状态压缩DP可以存储所有情况,再通过数学推导推导出递推公式,具体推导过程如下图。
其中状态转移数组有两个参数 a(压缩状态),b(硬币数)(可有可无,仅方便计算),值为从当前状态到抽完所需要抽数的期望。
然后根据下列推导,当前期望等于接下来所有可能的概率乘以其对应的期望+1,为什么加1,因为下一种情况必然多抽了一次。再根据数学推导得到状态转移方程。