头歌-机器学习第16次实验 EM算法

第1关：极大似然估计

任务描述

本关任务：根据本节课所学知识完成本关所设置的选择题。

相关知识

为了完成本关任务，你需要掌握：

什么是极大似然估计；
极大似然估计的原理；
极大似然估计的计算方法。

什么是极大似然估计

没有接触过或者没有听过”极大似然估计“的同学可能会被这个名词唬住（每个字都认识，但是连起来就不知道是什么意思了），我们不妨拆字释意。

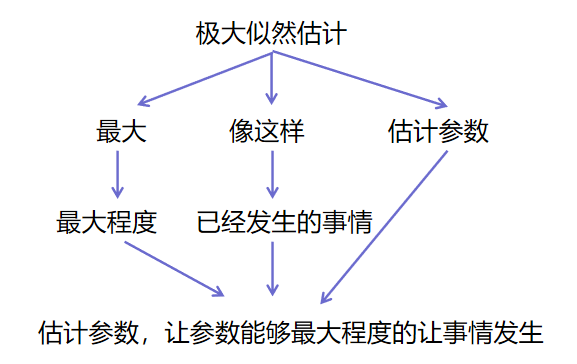
光看拆字释意后的解释可能还是有点绕。不如举个例子：一个袋子中总共有黑白两种颜色的球，总共有 100 个，其中一种颜色的球有 90 个。现在随机从袋子中取出一个球，发现是黑球。那么问你是黑色球有 90 个，还是白色球 90 个？

此时你可能会认为是黑色球有 90 个。因为随机抽取一个球，是黑色的(已经发生的事情)，说明黑色抽中的概率最大(最大程度)，因此猜测 90 个的是黑色球(估计)。这其实就是极大似然估计。

极大似然估计的原理

如果用数学语言来描述极大似然估计的话，就是如果事件的发生与参数heta有关，并假设事件发生时的样本为x1,...,xk，那么h^eta(x1,...,xk)就是参数heta的估计值。当heta=h^eta(x1,...,xk)时，表示当前样本发生的概率最大。

举个例子：在《权力的游戏》中有个场景，老徒利死的时候，尸体放在船上，需要弓箭手在岸边发射火箭引燃。但是当时的艾德慕·徒利公爵射了三箭都没中，布林登·徒利实在看不下去了，通过旗帜判断风向，一箭命中！因此箭能否射中靶心，不仅跟弓箭手的瞄准能力有关，还跟外界的风向有关系。假设不考虑人的因素，只考虑风的大小。同样的瞄准和力度，风太大不行、太小也不行。那我们如果给风的大小设置一个值为heta。假设一名弓箭手射出了三只箭，分别是8环、6环、7环(即x1=8,x2=6,x3=7)，当时风的大小为88。那么我们认为只有heta=88，发生上面事件的概率最大。

极大似然估计的计算方法

假设一个袋子装有白球与红球，比例未知，现在抽取 10 次（每次抽完都放回，保证事件独立性），假设抽到了 7 次白球和 3 次红球，在此数据样本条件下，你可能会下意识的认为袋子中白球的比例为 0.7，但是我们同样可以采用最大似然估计法求解袋子中白球的比例。

假设袋子中白球的比例为参数heta。简单起见，首先定义从袋子中随机抽取两次球摸到白球和红球的概率，如下（其中f表示模型，x1表示第一次摸球，x2表示第二次摸球）：

f(x1,x2∣heta)=f(x1∣heta)∗f(x2∣heta)

由于heta是未知的，所以我们将这个未知量heta放到一个函数中作为参数，这个函数称为似然函数。

L(heta∣x1,x2)=f(x1,x2∣heta)=prodi=12f(xi∣heta)

有了似然函数之后，很明显，就是想要知道当heta为何值时似然函数L得值最大。找到了这个heta就相当于完成了极大似然估计。那么怎么找呢？回忆一下高中所学的知识，会发现可以通过对heta求导。但是现在的似然函数L求导不方便，所以我们需要对似然函数L取对数处理。经过取对数处理后的似然函数通常称为对数似然函数。

lnL(heta∣x1,x2)=lnf(x1,x2∣heta)=sumi=12lnf(xi∣heta)

为了数学计算上更方便，通常会对对数似然函数求个均值，得到平均对数似然函数。

l^=21lnL(heta∣x1,x2)

若将找到的合适的heta表示为h^etamle，则有：

h^etamle=argmaxl^(heta∣x1,x2)

这是从袋子里随机抽取两个球的极大似然估计的数学表示。例子中是从袋子里随机抽取了十次球，根据刚刚所学的知识，我们能够很容易的进行扩展。假设抽取到白球的概率为heta，很显然抽取到红球的概率就是1−heta。所以从袋子里抽取十次，有七次是抽到白球的似然函数L可以表示为：

L(heta∣x1,x2,...,x10)=f(x1∣heta)∗f(x2∣heta)∗...∗f(x10∣heta)=heta7(1−heta)3

所以其平均对数似然函数可表示为:

hatl=101ln(heta7(1−heta)3)

接下来就可以对heta求导，并令导数为0。

l^=7heta6(1−heta)3−3heta7(1−heta)2=0=>heta=0.7

我们会发现通过极大似然估计法计算出的白球的比例与我们下意识的判断一致。