OJ:P1429 平面最近点对(加强版) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
非常详细的博客:平面上最近点对 - 洛谷专栏 (luogu.com.cn)
更正式的文章:平面最近点对 - OI Wiki
这也是我们算法课的一个实验。不过我做的不好,我只会简单的分治,中间区域合并时用的还是蛮力QAQ。
分治学好后,难点其实在合并这里的处理。(直接想极端情况吧,所有点的x都相同)
————————
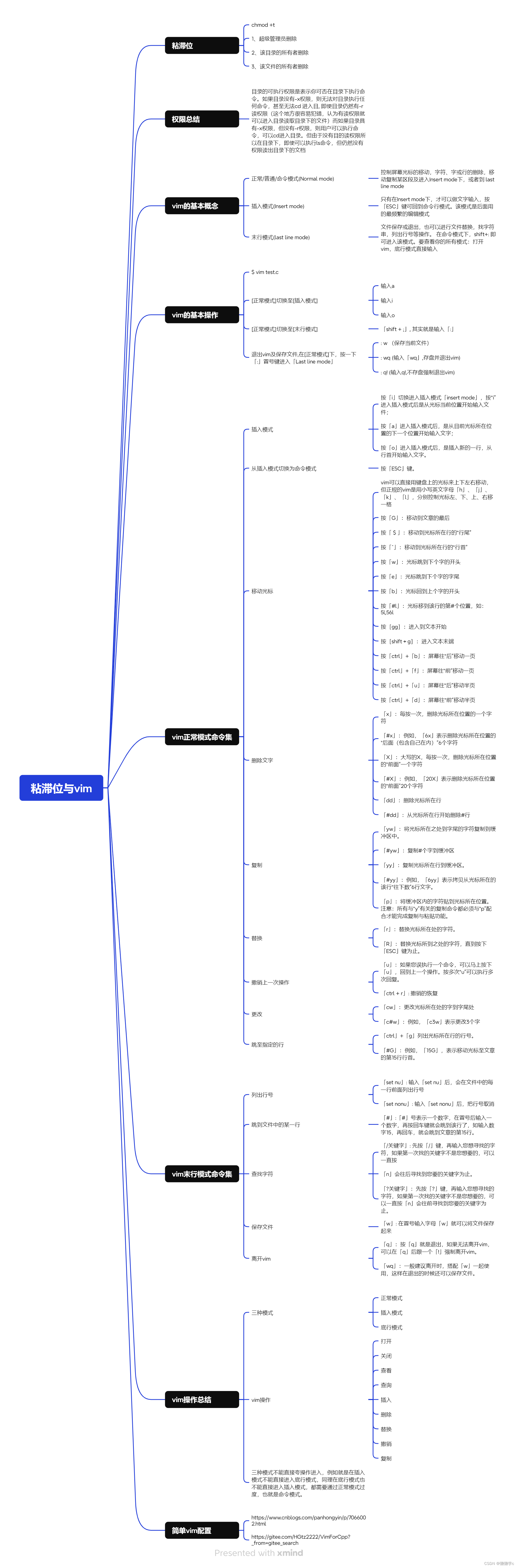
图解总思路:
1.分治:
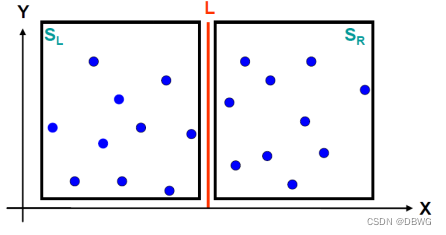
————
2.中间处理部分:
(注意我们是用序号排的序,二分也是根据序号二分)
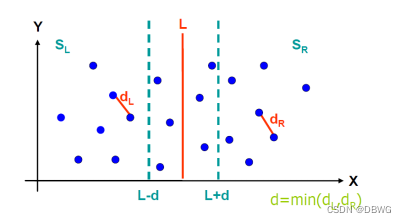
这个中线可以是“mid点”
理解:
其实极端情况就是存在更近点对且mid离他们很远。注意这两个点的x和y都是很近的,距离小于d,而他们离mid的x也绝对都小于d,所以是在范围内的。
所以这个2d其实可以再缩减,mid向右d 与 mid+1向左d 的交集 ,如果是mid或者mid+1能有更近点对,那么这个d是足够的,再远点x都大于d了。
————
3.中间合并部分
对于每个左边的点比如P,最多检查右边这六个点。
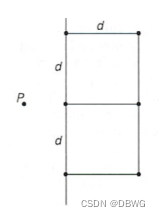
其实最多五个,右边三个距离肯定大于d了。
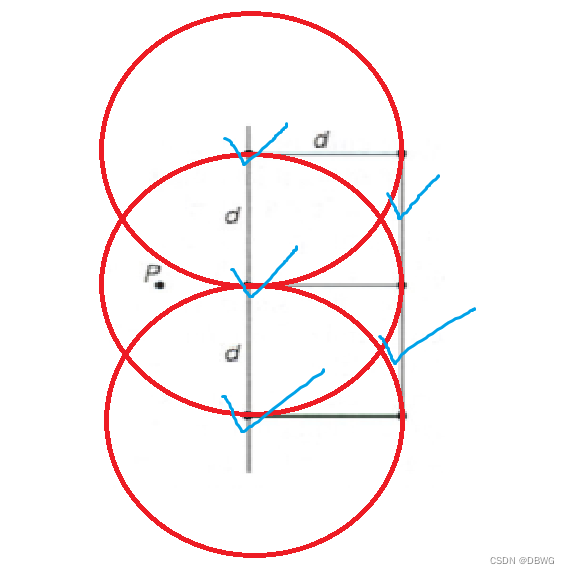
但如何做到高效比较呢,只能将中间部分左右的所有点排个序,一起比了。
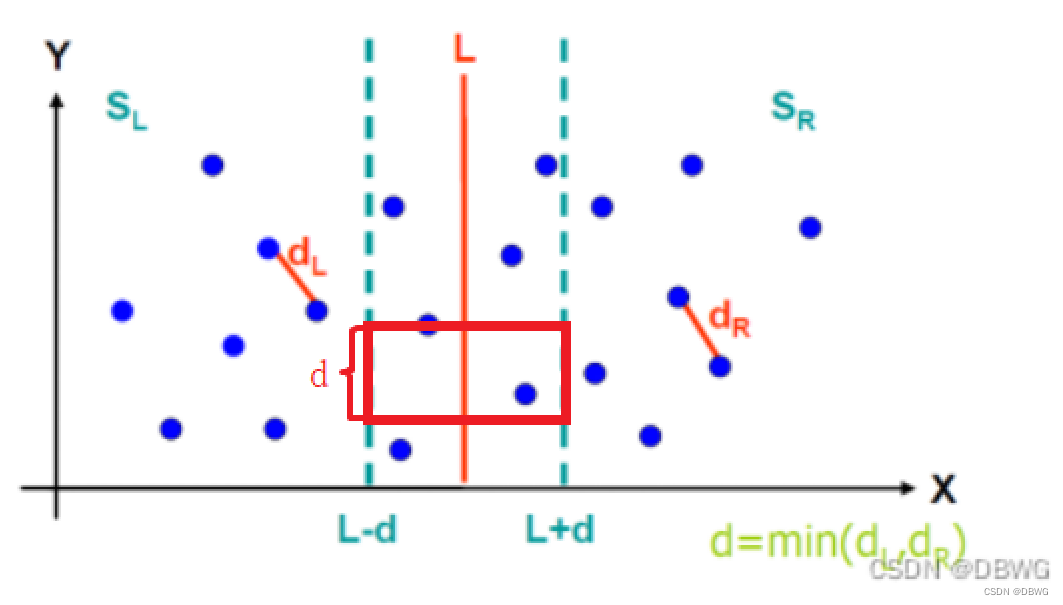
根据y坐标排序,
每个点比后面的点,直到纵坐标之差超过d。
排序O(nlongn) , 比较O(5n) (这里比较只比自己下面的,左边也可能下面也有一个d,见下图)
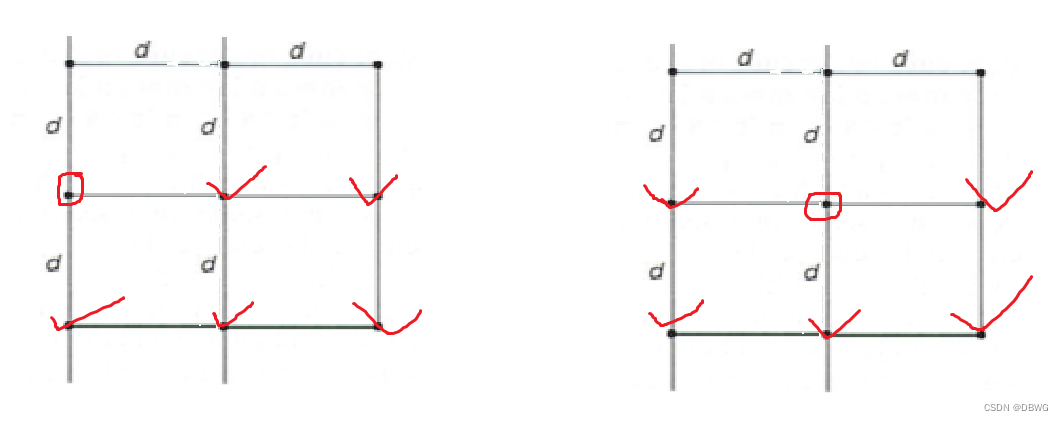
合并部分总的就是O(nlongn + n)
————
总的时间复杂度:
加上分治的时间复杂度结果为 2nlongn + n ,即 nlongn
参考代码:
#define ll long long
#define endl "\n"
//#define int long long
#define PII pair<int,int>
const int maxn = 100000;struct Point
{int x, y;
};double distance(const Point& a, const Point& b)
{return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2));
}vector<Point>arr;
double mindis = DBL_MAX;
pair<Point, Point> closestPair;
Point tmp[maxn + 10];void brute_force()
{for (int i = 0; i < arr.size(); i++){for (int j = i + 1; j < arr.size(); j++){double aim = distance(arr[i], arr[j]);if (aim < mindis){mindis = aim;closestPair = { arr[i],arr[j] };}}}
}double fmerge(int l, int r)
{double dis = DBL_MAX;if (r - l < 3){for (int i = l; i < r; i++){for (int j = i + 1; j <= r; j++){double aim = distance(arr[i], arr[j]);if (aim < dis)//当前最小{dis = aim;if (dis < mindis)//总最小{mindis = dis;closestPair = { arr[i],arr[j] };}}}}return dis;}int m = l + ((r - l) >> 1);double d1 = fmerge(l, m);double d2 = fmerge(m + 1, r);dis = min(d1, d2);int tot = 0;for (int i = l; i <= r; i++){if (fabs(arr[i].x - arr[m].x) <= dis){tmp[tot++] = arr[i];}}sort(tmp, tmp + tot, [&](Point a, Point b) {return a.y < b.y;});for (int i = 0; i < tot; i++){for (int j = i + 1; j < tot && tmp[j].y - tmp[i].y <= dis; j++){double aim = distance(tmp[i], tmp[j]);if (aim < dis)//当前最小{dis = aim;if (dis < mindis)//总最小{mindis = dis;closestPair = { tmp[i],tmp[j] };}}}}return dis;
}void findTwoPointsWithTheShortestDistance()
{int size = arr.size();sort(arr.begin(), arr.end(), [&](const Point& a, const Point& b) {if (a.x == b.x)return a.y < b.y;//return a.y <= b.y;return a.x < b.x;});fmerge(0, size - 1);
}void solve()
{int n;cin >> n;arr = vector<Point>(n);for (int i = 0; i < n; i++){int a, b;cin >> a >> b;arr[i] = { a,b };}findTwoPointsWithTheShortestDistance();//cout << mindis << endl;printf("%.4lf", mindis);
}