求最大公约数：辗转相除法
int gcd(int a,int b){return b==0?a:gcd(b,a%b);
}
求最小公倍数：两整数之积除以最大公约数
int lcm(int a, int b){return a*b / gcd(a, b);
}
十进制转n进制：
char get(int x){if(x<=9){return x+'0';}else{return (x-10)+'A';}
}
string base(int x) // 十进制转 n进制
{string num;while(x){num += get(x % n), x /= n;}reverse(num.begin(),num.end());return num;
}
c语言输出
printf（"%02d", a）
表示输出按俩位输出整形a，比如a=8，则输出08，a=24，输出24
printf("%.2f",a)
表示输出浮点数a小数点后俩位，比如a=8,则输出8.00，a=1.123，则输出a=1.12
最短路径问题
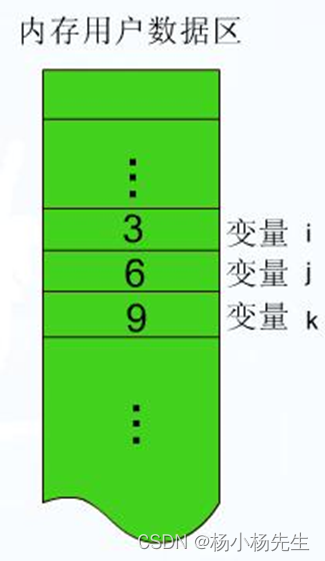
什么是链式前向星实现邻接表
链式前向星实现：设置三个数组，一个数组h用来存节点，一个数组e用来存值，一个数组ne用来存下一个节点。我们需要设置索引idx来实现ne的查找，不然没法链接起来
void add(int a,int b) {
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
例：
我们遍历的话就是从h[1]开始遍历，此时h[1]=4，然后我们找下一个节点，下一个节点对应的索引就是3，再下一个节点对应的索引就是0，当索引为-1时结束。这个过程next实际上是向前走的，关系又是链式的，因此成为链式前向星
为什么要用memset(dist,0x3f,sizeof dist)来初始化
回答:：0x3f3f3f3f的十进制是1061109567，是1e9级别的（和0x7fffffff一个数量级，0x7fffffff代表了32-bit int的最大值），而一般场合下的数据都是小于1e9的，所以它可以作为无穷大使用而不致出现数据大于无穷大的情形。 另一方面，由于一般的数据都不会大于10^9，所以当我们把无穷大加上一个数据时，它并不会溢出（这就满足了“无穷大加一个有穷的数依然是无穷大”），事实上0x3f3f3f3f+0x3f3f3f3f=2122219134，这非常大但却没有超过32-bit int的表示范围，所以0x3f3f3f3f还满足了我们“无穷大加无穷大还是无穷大”的需求。
floyd
E.路径（12届蓝桥杯c++B组第一场省赛）
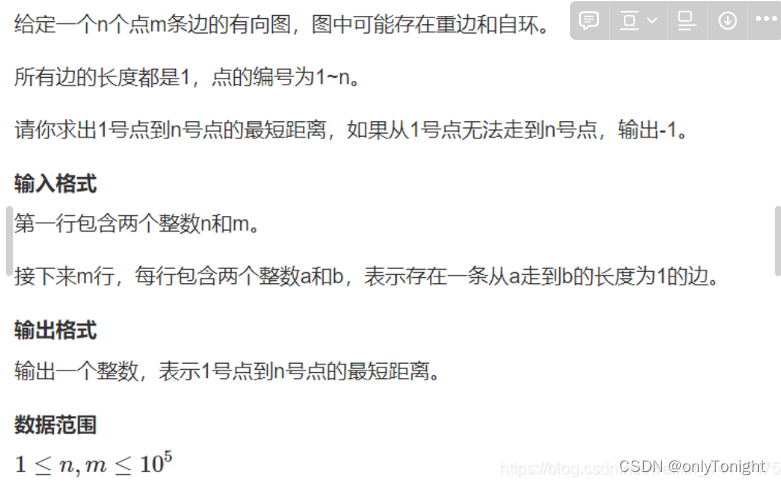
小蓝学习了最短路径之后特别高兴，他定义了一个特别的图，希望找到图中的最短路径。
小蓝的图由 2021 个结点组成，依次编号 1 至 2021。
对于两个不同的结点 a, b，如果 a 和 b 的差的绝对值大于 21，则两个结点之间没有边相连；如果 a 和 b 的差的绝对值小于等于 21，则两个点之间有一条长度为 a 和 b 的最小公倍数的无向边相连。
例如：结点 1 和结点 23 之间没有边相连；结点 3 和结点 24 之间有一条无向边，长度为 24；结点 15 和结点 25 之间有一条无向边，长度为 75。
请计算，结点 1 和结点 2021 之间的最短路径长度是多少。
提示：建议使用计算机编程解决问题。
#include <iostream>
#include <cmath>
#include <cstring>
using namespace std;
const int N = 3000;
int n = 2021;
int g[N][N];
// 求最小公约数
int gcd(int a, int b) {return b ? gcd(b, a % b) : a;
}void floyb() {for (int t = 1; t <= n; ++ t) {for (int i = 1; i <= n; ++ i) {for (int j = 1; j <= n; ++ j) {g[i][j] = min(g[i][j], g[i][t] + g[t][j]);}}}
}
int main (){memset(g, 0x3f, sizeof g);for (int i = 1; i <= n; ++ i) {for (int j = 1; j <= n; ++ j) {if (abs(i - j) <= 21) {// 最大公倍数求法g[i][j] = i * j / gcd(i, j);}}}floyb();cout << g[1][n] << endl;return 0;
}
并查集
小蓝要用七段码数码管来表示一种特殊的文字。
上图给出了七段码数码管的一个图示，数码管中一共有 7 段可以发光的二 极管，分别标记为 a, b, c, d, e, f, g。
小蓝要选择一部分二极管（至少要有一个）发光来表达字符。在设计字符 的表达时，要求所有发光的二极管是连成一片的。
例如： b 发光，其他二极管不发光可以用来表达一种字符。
例如： c 发光，其他二极管不发光可以用来表达一种字符。这种 方案与上 一行的方案可以用来表示不同的字符，尽管看上去比较相似。
例如： a, b, c, d, e 发光， f, g 不发光可以用来表达一种字符。
例如： b, f 发光，其他二极管不发光则不能用来表达一种字符，因为发光 的二极管没有连成一片。
请问，小蓝可以用七段码数码管表达多少种不同的字符？
【答案提交】 这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。
#include<bits/stdc++.h>
using namespace std;
const int N=10;
int e[N][N],use[N],ans=0,fa[N];
int find(int f){//查找父值 if(fa[f]==f){return f;}return find(fa[f]);
}
void dfs(int n){if(n>7){for(int i=1;i<=7;i++){fa[i]=i;//每个元素单独成一个集合 }for(int i=1;i<=7;i++){//遍历每条边 for(int j=1;j<=7;j++){if(e[i][j]&&use[i]&&use[j]){//如果ij连通且都已打开，使它们的父集相等 int fx=find(i),fy=find(j);if(fx!=fy){fa[fx]=fy;//合并集合：即让它们的父值相等 }}}}int k=0;for(int i=1;i<=7;i++){ if(fa[i]==i&&use[i]){//判断现有元素有几个集合 k++;}}if(k==1){//如果已使用的灯在一个集合内：即父集只有一个元素 ans++;}return ;}use[n]=1;dfs(n+1);use[n]=0;dfs(n+1);
}
int main(){e[1][2]=e[1][6]=1;e[2][3]=e[2][7]=1;e[3][4]=e[3][7]=1;e[4][5]=1;e[5][6]=e[5][7]=1;e[6][7]=1;dfs(1);cout<<ans<<endl;return 0;
}
getline（）
接收一个字符串，可以接收空格并输出，读取缓冲区的回车然后舍弃
#include<iostream>
#include<string>
using namespace std;
main ()
{
string str;
getline(cin,str);
cout<<str<<endl;
}
输入：jkljkljkl
输出：jkljkljkl
输入：jkl jfksldfj jklsjfl
输出：jkl jfksldfj jklsjfl
push_back()
push_back() 在Vector最后添加一个元素（参数为要插入的值）
vector<int> vec;
vec.push_back(10);
//在容器中添加10
或者再string中最后插入一个字符；
string str;
str.push_back('d');
类似的：
pop_back() //移除最后一个元素
clear() //清空所有元素
empty() //判断vector是否为空，如果返回true为空
erase() // 删除指定元素
