复杂DP算法
- 一、线性DP
- 例题
- 1、鸣人的影分身
- 题目信息
- 思路
- 题解
- 2、糖果
- 题目信息
- 思路
- 题解
- 二、区间DP
- 例题
- 密码脱落
- 题目信息
- 思路
- 题解
- 三、树状DP
- 例题
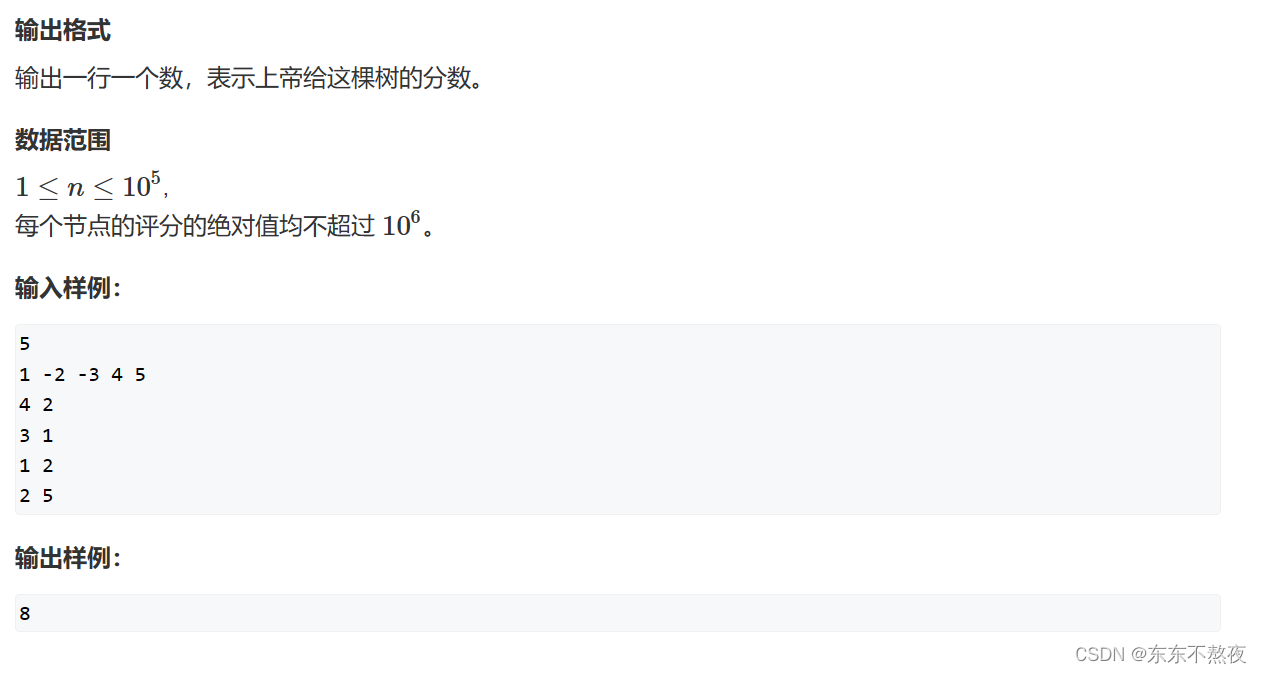
- 生命之树
- 题目信息
- 思路
- 题解
一、线性DP
例题
1、鸣人的影分身
题目信息

思路

题解
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
#define maxsize 20
using namespace std;int t,m,n;
int f[maxsize][maxsize];signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>t;while(t--){cin>>m>>n;f[0][0]=1;for(int i=0;i<=m;i++){for(int j=1;j<=n;j++){f[i][j]=f[i][j-1];if(i>=j) f[i][j] +=f[i-j][j];}}cout<<f[m][n]<<endl;}return 0;
}
2、糖果
题目信息

思路

题解
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
#define maxsize 200
using namespace std;int n,k;
int f[maxsize][maxsize];signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>k;memset(f,-0x3f,sizeof(f));f[0][0]=0;for(int i=1;i<=n;i++){int w;cin>>w;for(int j=0;j<k;j++){f[i][j]=max(f[i-1][j],f[i-1][(j+k-w%k)%k]+w);}}cout<<f[n][0]<<endl;return 0;
}二、区间DP
例题
密码脱落
题目信息

思路

题解
#include <bits/stdc++.h>
#define maxsize 1010
#define endl '\n'
#define int long long
using namespace std;char str[maxsize];
int f[maxsize][maxsize];signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>str;int n=strlen(str);for(int len=1;len<=n;len++){for(int l=0;l+len-1-1<n;l++){int r=l+len-1;if(len==1) f[l][r]=1;else{if(str[l]==str[r]) f[l][r]=f[l+1][r-1]+2;if(f[l+1][r]>f[l][r]) f[l][r]=f[l+1][r];if(f[l][r-1]>f[l][r]) f[l][r]=f[l][r-1];}}}cout<<n-f[0][n-1]<<endl;return 0;
}
三、树状DP
例题
生命之树
题目信息