Offer必备算法26_BFS解决最短路_四道力扣题（由易到难）

①力扣1926. 迷宫中离入口最近的出口

解析代码

②力扣433. 最小基因变化

解析代码

③力扣127. 单词接龙

解析代码

④力扣675. 为高尔夫比赛砍树

解析代码

本篇完。

①力扣1926. 迷宫中离入口最近的出口

1926. 迷宫中离入口最近的出口

难度中等

给你一个 m x n 的迷宫矩阵 maze （下标从 0 开始），矩阵中有空格子（用 '.' 表示）和墙（用 '+' 表示）。同时给你迷宫的入口 entrance ，用 entrance = [entrancerow, entrancecol] 表示你一开始所在格子的行和列。

每一步操作，你可以往上，下，左或者右移动一个格子。你不能进入墙所在的格子，你也不能离开迷宫。你的目标是找到离 entrance 最近的出口。出口的含义是 maze 边界上的 空格子。entrance 格子不算出口。

请你返回从 entrance 到最近出口的最短路径的步数，如果不存在这样的路径，请你返回 -1 。

示例 1：

输入：maze = [["+","+",".","+"],[".",".",".","+"],["+","+","+","."]], entrance = [1,2]
输出：1
解释：总共有 3 个出口，分别位于 (1,0)，(0,2) 和 (2,3) 。
一开始，你在入口格子 (1,2) 处。
- 你可以往左移动 2 步到达 (1,0) 。
- 你可以往上移动 1 步到达 (0,2) 。
从入口处没法到达 (2,3) 。
所以，最近的出口是 (0,2) ，距离为 1 步。

示例 2：

输入：maze = [["+","+","+"],[".",".","."],["+","+","+"]], entrance = [1,0]
输出：2
解释：迷宫中只有 1 个出口，在 (1,2) 处。
(1,0) 不算出口，因为它是入口格子。
初始时，你在入口与格子 (1,0) 处。
- 你可以往右移动 2 步到达 (1,2) 处。
所以，最近的出口为 (1,2) ，距离为 2 步。

示例 3：

输入：maze = [[".","+"]], entrance = [0,0]
输出：-1
解释：这个迷宫中没有出口。

提示：

maze.length == m
maze[i].length == n
1 <= m, n <= 100
maze[i][j] 要么是 '.' ，要么是 '+' 。
entrance.length == 2
0 <= entrancerow < m
0 <= entrancecol < n
entrance 一定是空格子。

class Solution {
public:int nearestExit(vector<vector<char>>& maze, vector<int>& entrance) {}
};

解析代码

利用层序遍历来解决迷宫问题，是最经典的做法。我们可以从起点开始层序遍历，并且在遍历的过程中记录当前遍历的层数。这样就能在找到出口的时候，得到起点到出口的最短距离。

class Solution {int dx[4] = {0, 0, -1, 1};int dy[4] = {1, -1, 0, 0};
public:int nearestExit(vector<vector<char>>& maze, vector<int>& entrance) {int m = maze.size(), n = maze[0].size(), ret = 0;vector<vector<bool>> vis(m, vector<bool>(n, false)); // 下标是否被访问过queue<vector<int>> q; // 存下标的队列q.push(entrance);   // 入口入队vis[entrance[0]][entrance[1]] = true;while(!q.empty()){++ret; // 一层加一次步数int size = q.size();for(int i = 0; i < size; ++i) // 访问当前层{vector<int> tmp = q.front();q.pop();for(int j = 0; j < 4; ++j){int x = tmp[0] + dx[j], y = tmp[1] + dy[j];if(x >= 0 && x < m && y >= 0 && y < n && maze[x][y] == '.' && !vis[x][y]){if(x == 0 || x == m - 1 || y == 0 || y == n - 1)return ret; // 是出口就返回q.push({x, y});vis[x][y] = true;}}}}return -1;}
};

②力扣433. 最小基因变化

433. 最小基因变化

难度中等

基因序列可以表示为一条由 8 个字符组成的字符串，其中每个字符都是 'A'、'C'、'G' 和 'T' 之一。

假设我们需要调查从基因序列 start 变为 end 所发生的基因变化。一次基因变化就意味着这个基因序列中的一个字符发生了变化。

例如，"AACCGGTT" --> "AACCGGTA" 就是一次基因变化。

另有一个基因库 bank 记录了所有有效的基因变化，只有基因库中的基因才是有效的基因序列。（变化后的基因必须位于基因库 bank 中）

给你两个基因序列 start 和 end ，以及一个基因库 bank ，请你找出并返回能够使 start 变化为 end 所需的最少变化次数。如果无法完成此基因变化，返回 -1 。

注意：起始基因序列 start 默认是有效的，但是它并不一定会出现在基因库中。

示例 1：

输入：start = "AACCGGTT", end = "AACCGGTA", bank = ["AACCGGTA"]
输出：1

示例 2：

输入：start = "AACCGGTT", end = "AAACGGTA", bank = ["AACCGGTA","AACCGCTA","AAACGGTA"]
输出：2

示例 3：

输入：start = "AAAAACCC", end = "AACCCCCC", bank = ["AAAACCCC","AAACCCCC","AACCCCCC"]
输出：3

提示：

start.length == 8
end.length == 8
0 <= bank.length <= 10
bank[i].length == 8
start、end 和 bank[i] 仅由字符 ['A', 'C', 'G', 'T'] 组成

class Solution {
public:int minMutation(string startGene, string endGene, vector<string>& bank) {}
};

解析代码

如果将每次字符串的变换抽象成图中的两个顶点和一条边的话，问题就变成了边权为 1 的最短路问题。因此，从起始的字符串开始，来一次 bfs 即可。

class Solution {
public:int minMutation(string startGene, string endGene, vector<string>& bank) {unordered_set<string> bankHash(bank.begin(), bank.end());unordered_set<string> vis;string chargeArr = "ACGT";if(startGene == endGene)return 0;if(!bankHash.count(endGene))return -1;int ret = 0;queue<string> q;q.push(startGene);vis.insert(startGene);while(!q.empty()){++ret;int size = q.size();for(int i = 0; i < size; ++i){string t = q.front();q.pop();for(int j = 0; j < 8; ++j){for(int k = 0; k < 4; ++k){string tmp = t;tmp[j] = chargeArr[k];if(bankHash.count(tmp) && !vis.count(tmp)) // 有效的且没访问过{if(tmp == endGene)return ret;q.push(tmp);vis.insert(tmp);}}}}}return -1;}
};

③力扣127. 单词接龙

127. 单词接龙

难度困难

字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk：

每一对相邻的单词只差一个字母。
对于 1 <= i <= k 时，每个 si 都在 wordList 中。注意， beginWord 不需要在 wordList 中。
sk == endWord

给你两个单词 beginWord 和 endWord 和一个字典 wordList ，返回从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列，返回 0 。

示例 1：

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出：5
解释：一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。

示例 2：

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
输出：0
解释：endWord "cog" 不在字典中，所以无法进行转换。

提示：

1 <= beginWord.length <= 10
endWord.length == beginWord.length
1 <= wordList.length <= 5000
wordList[i].length == beginWord.length
beginWord、endWord 和 wordList[i] 由小写英文字母组成
beginWord != endWord
wordList 中的所有字符串 互不相同

class Solution {
public:int ladderLength(string beginWord, string endWord, vector<string>& wordList) {}
};

解析代码

和力扣433. 最小基因变化一样，如果将每次字符串的变换抽象成图中的两个顶点和一条边的话，问题就变成了边权为 1 的最短路问题。因此，从起始的字符串开始，来一次 bfs 即可。

class Solution {
public:int ladderLength(string beginWord, string endWord, vector<string>& wordList) {unordered_set<string> wordListHash(wordList.begin(), wordList.end());unordered_set<string> vis;if(!wordListHash.count(endWord))return 0;int ret = 1;queue<string> q;q.push(beginWord);vis.insert(beginWord);while(!q.empty()){++ret;int size = q.size();while(size--){string t = q.front();q.pop();for(int i = 0; i < t.size(); ++i){for(char ch = 'a'; ch <= 'z'; ++ch){string tmp = t;tmp[i] = ch;if(wordListHash.count(tmp) && !vis.count(tmp)){if(tmp == endWord)return ret;q.push(tmp);vis.insert(tmp);}}}}}return 0;}
};

④力扣675. 为高尔夫比赛砍树

675. 为高尔夫比赛砍树

难度困难

你被请来给一个要举办高尔夫比赛的树林砍树。树林由一个 m x n 的矩阵表示，在这个矩阵中：

0 表示障碍，无法触碰
1 表示地面，可以行走
比 1 大的数 表示有树的单元格，可以行走，数值表示树的高度

每一步，你都可以向上、下、左、右四个方向之一移动一个单位，如果你站的地方有一棵树，那么你可以决定是否要砍倒它。

你需要按照树的高度从低向高砍掉所有的树，每砍过一颗树，该单元格的值变为 1（即变为地面）。

你将从 (0, 0) 点开始工作，返回你砍完所有树需要走的最小步数。如果你无法砍完所有的树，返回 -1 。

可以保证的是，没有两棵树的高度是相同的，并且你至少需要砍倒一棵树。

示例 1：

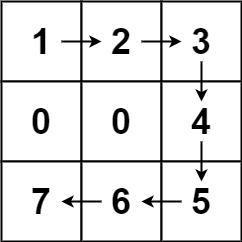
输入：forest = [[1,2,3],[0,0,4],[7,6,5]]
输出：6
解释：沿着上面的路径，你可以用 6 步，按从最矮到最高的顺序砍掉这些树。

示例 2：

输入：forest = [[1,2,3],[0,0,0],[7,6,5]]
输出：-1
解释：由于中间一行被障碍阻塞，无法访问最下面一行中的树。

示例 3：

输入：forest = [[2,3,4],[0,0,5],[8,7,6]]
输出：6
解释：可以按与示例 1 相同的路径来砍掉所有的树。
(0,0) 位置的树，可以直接砍去，不用算步数。

提示：

m == forest.length
n == forest[i].length
1 <= m, n <= 50
0 <= forest[i][j] <= 10^9

class Solution {
public:int cutOffTree(vector<vector<int>>& forest) {}
};

解析代码

先找出砍树的顺序，然后按照砍树的顺序，一个一个地用 bfs 求出最短路即可。求最短路就是力扣1926. 迷宫中离入口最近的出口。

class Solution {int dx[4] = {0, 0, -1, 1};int dy[4] = {1, -1, 0, 0};int m = 0, n = 0;bool vis[51][51];public:int cutOffTree(vector<vector<int>>& forest) {m = forest.size(), n = forest[0].size();map<int, pair<int,int>> hash; // 数组值和下标，按数组值排序for(int i = 0; i < m; ++i){for(int j = 0; j < n; ++j){if(forest[i][j] > 1) // 0不可走，1是地面hash[forest[i][j]] = {i, j};}}int ret = 0;pair<int,int> start = make_pair(0, 0);for(auto& [e, end] : hash) // 取下标{int step = bfs(forest, start, end);if(step == -1)return -1;ret += step;start = end;}return ret;}int bfs(vector<vector<int>>& forest, pair<int,int> start, pair<int,int> end){if(start == end)return 0;memset(vis, 0, sizeof(vis)); // 清空之前的数据queue<pair<int, int>> q;q.push(start);auto [a, b] = q.front();vis[a][b] = true;int ret = 0;while(!q.empty()){++ret;int sz = q.size();while(sz--){auto [a, b] = q.front();q.pop();for(int i = 0; i < 4; ++i){int x = a + dx[i], y = b + dy[i];if(x >= 0 && x < m && y >= 0 && y < n && forest[x][y] && !vis[x][y]){if(x == end.first && y == end.second)return ret;q.push({x, y});vis[x][y] = true;}}}}return -1;}
};