力扣题目链接

class Solution {
public:int integerBreak(int n) {vector<int> dp(n + 1);dp[2] = 1;for (int i = 3; i <= n ; i++) {for (int j = 1; j <= i / 2; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}}return dp[n];}
};

思路

看到这道题目，都会想拆成两个呢，还是三个呢，还是四个....

我们来看一下如何使用动规来解决。

#动态规划

动规五部曲，分析如下：

1. 确定dp数组（dp table）以及下标的含义

dp[i]：分拆数字i，可以得到的最大乘积为dp[i]。

dp[i]的定义将贯彻整个解题过程，下面哪一步想不懂了，就想想dp[i]究竟表示的是啥！

1. 确定递推公式

可以想 dp[i]最大乘积是怎么得到的呢？

其实可以从1遍历j，然后有两种渠道得到dp[i].

一个是j * (i - j) 直接相乘。

一个是j * dp[i - j]，相当于是拆分(i - j)，对这个拆分不理解的话，可以回想dp数组的定义。

那有同学问了，j怎么就不拆分呢？

j是从1开始遍历，拆分j的情况，在遍历j的过程中其实都计算过了。那么从1遍历j，比较(i - j) * j和dp[i - j] * j 取最大的。递推公式：dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));

也可以这么理解，j * (i - j) 是单纯的把整数拆分为两个数相乘，而j * dp[i - j]是拆分成两个以及两个以上的个数相乘。

如果定义dp[i - j] * dp[j] 也是默认将一个数强制拆成4份以及4份以上了。

所以递推公式：dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});

那么在取最大值的时候，为什么还要比较dp[i]呢？

因为在递推公式推导的过程中，每次计算dp[i]，取最大的而已。

1. dp的初始化

不少同学应该疑惑，dp[0] dp[1]应该初始化多少呢？

有的题解里会给出dp[0] = 1，dp[1] = 1的初始化，但解释比较牵强，主要还是因为这么初始化可以把题目过了。

严格从dp[i]的定义来说，dp[0] dp[1] 就不应该初始化，也就是没有意义的数值。

拆分0和拆分1的最大乘积是多少？

这是无解的。

这里我只初始化dp[2] = 1，从dp[i]的定义来说，拆分数字2，得到的最大乘积是1，这个没有任何异议！

1. 确定遍历顺序

确定遍历顺序，先来看看递归公式：dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));

dp[i] 是依靠 dp[i - j]的状态，所以遍历i一定是从前向后遍历，先有dp[i - j]再有dp[i]。

所以遍历顺序为：

for (int i = 3; i <= n ; i++) {for (int j = 1; j < i - 1; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}
}

注意 枚举j的时候，是从1开始的。从0开始的话，那么让拆分一个数拆个0，求最大乘积就没有意义了。

j的结束条件是 j < i - 1 ，其实 j < i 也是可以的，不过可以节省一步，例如让j = i - 1，的话，其实在 j = 1的时候，这一步就已经拆出来了，重复计算，所以 j < i - 1

至于 i是从3开始，这样dp[i - j]就是dp[2]正好可以通过我们初始化的数值求出来。

更优化一步，可以这样：

for (int i = 3; i <= n ; i++) {for (int j = 1; j <= i / 2; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}
}

因为拆分一个数n 使之乘积最大，那么一定是拆分成m个近似相同的子数相乘才是最大的。

例如 6 拆成 3 * 3， 10 拆成 3 * 3 * 4。 100的话 也是拆成m个近似数组的子数 相乘才是最大的。

只不过我们不知道m究竟是多少而已，但可以明确的是m一定大于等于2，既然m大于等于2，也就是 最差也应该是拆成两个相同的 可能是最大值。

那么 j 遍历，只需要遍历到 n/2 就可以，后面就没有必要遍历了，一定不是最大值。

至于 “拆分一个数n 使之乘积最大，那么一定是拆分成m个近似相同的子数相乘才是最大的” 这个我就不去做数学证明了，感兴趣的同学，可以自己证明。

1. 举例推导dp数组

举例当n为10 的时候，dp数组里的数值，如下：

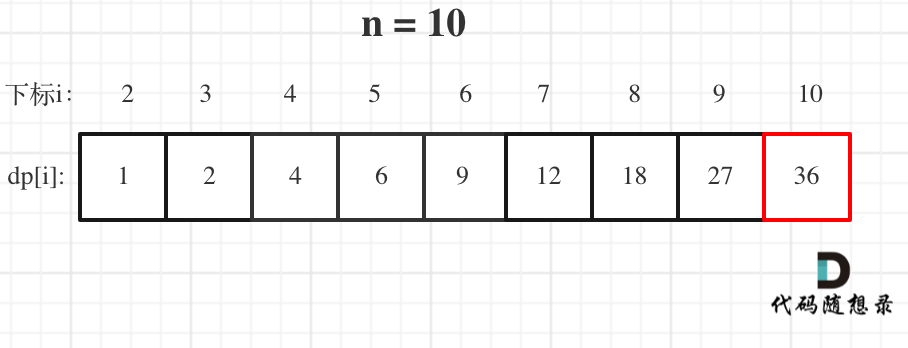
自己的思路： 

拆成m个数相加

而m个数尽可能多且差不多大

最大乘积：

i拆 得到最大乘积dp[i]

还是有点难懂

动态规划，本题关键在于理解递推公式！| LeetCode：343. 整数拆分_哔哩哔哩_bilibili