目标

假设您是一家餐厅连锁店的首席执行官，并正在考虑在不同的城市开设新店。您希望将您的业务扩展到可能为您的餐厅带来更高利润的城市。该连锁店已经在各个城市设有餐厅，您已经获得了这些城市的利润和人口数据。您还拥有关于新餐厅候选城市的数据。对于这些城市，您拥有城市人口数据。您能否使用数据帮助您确定哪些城市可能会为您的业务带来更高的利润？（主要就是自己实现一元线性回归的成本函数，梯度下降）

1.熟悉我们的训练集

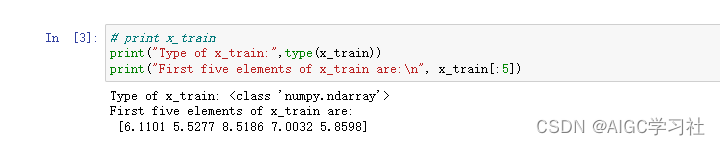
• x表示不同城市人口数量，y表示该城市餐厅的盈利。
• 查看部分城市人口，6.1101 表示该城市的人口为 61101。
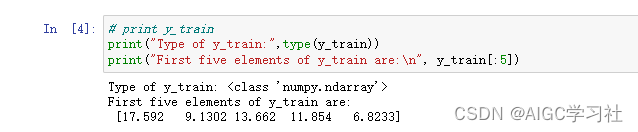
• 查看部分城市利润，17.592表示盈利17.592万美金，负数表示亏损。
• 查看训练样本的数量。
  
• 可视化训练样本数据（人口和利润），更多的属性也可以用散点图可视化。

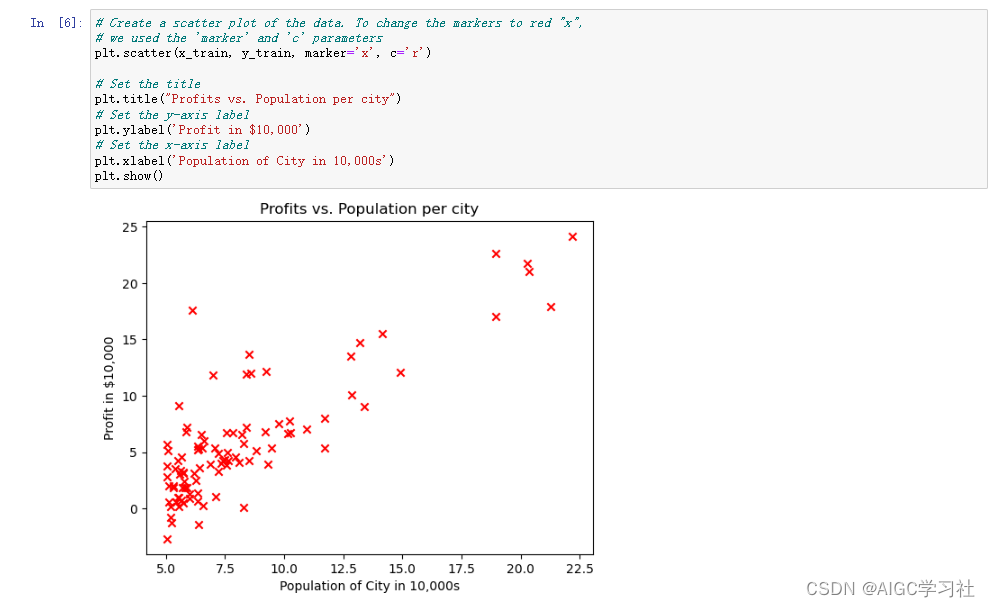
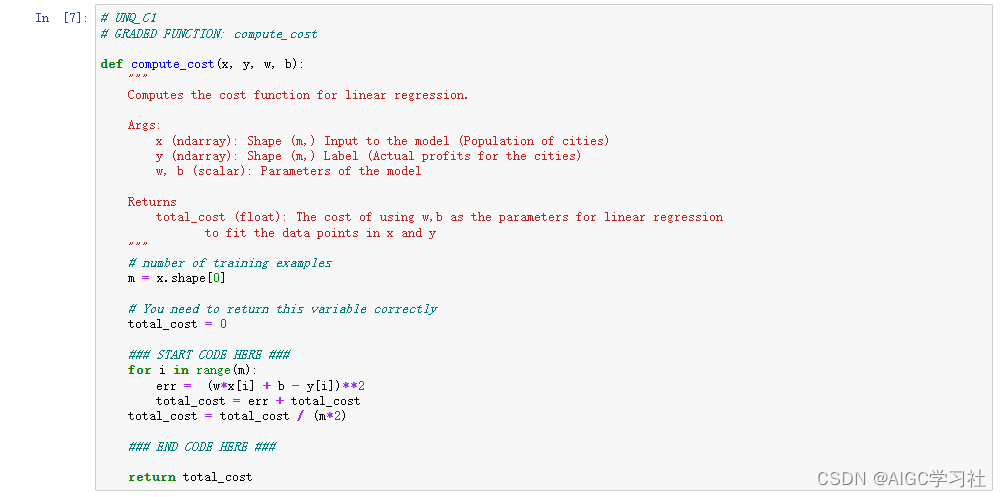
2.计算成本函数（从START CODE HERE自己编写）

• err表示线性回归函数计算的预测值减去真实值，差值平方，然后最终结果求和。
• 验证我们写的函数是否正确。
  

3.计算梯度下降（从START CODE HERE自己编写）

• 目前接触的都是批量梯度下降，也就是每执行一次梯度下降，都计算所有训练样本，而梯度下降的过程是多次迭代的。
  
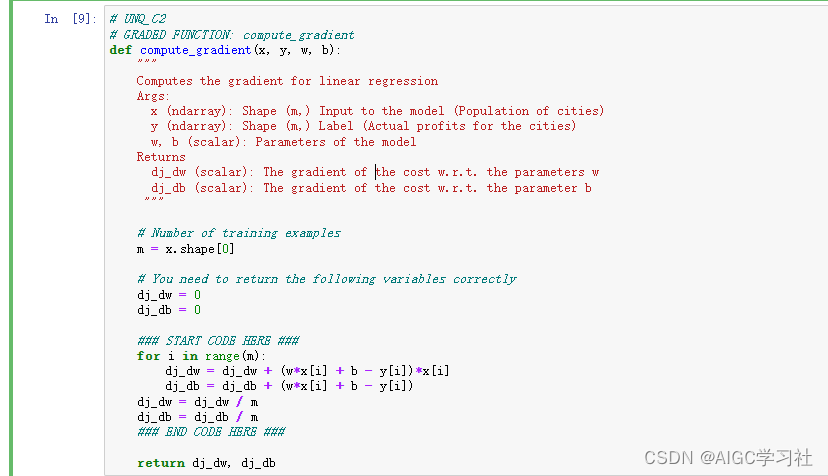
• 执行一次梯度下降的w，b，正确与否只看函数写的对不对，不看最终w，b的结果。
  
• 不断迭代梯度下降。
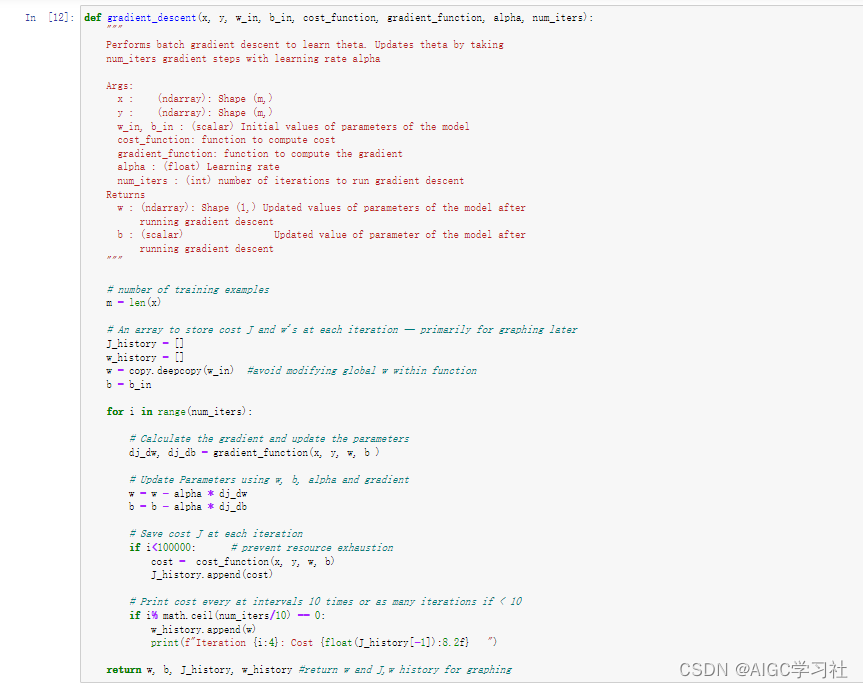
• 设置迭代次数为1500，运行上述函数，得到最优w，b。

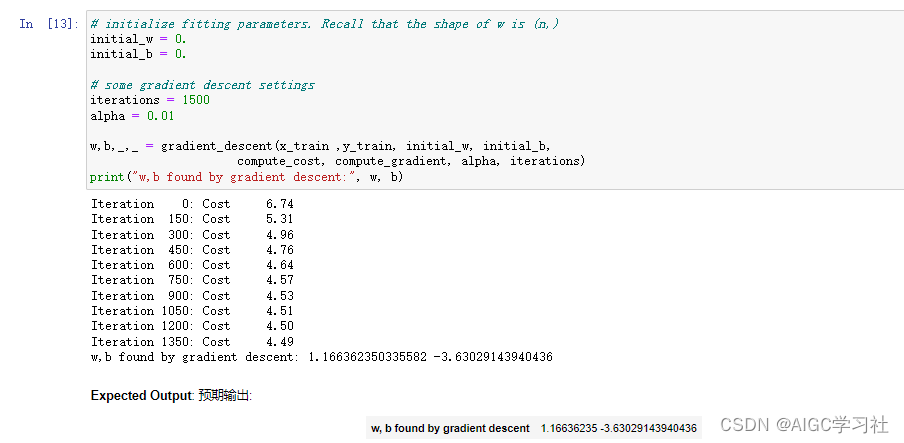
4.使用模型预测

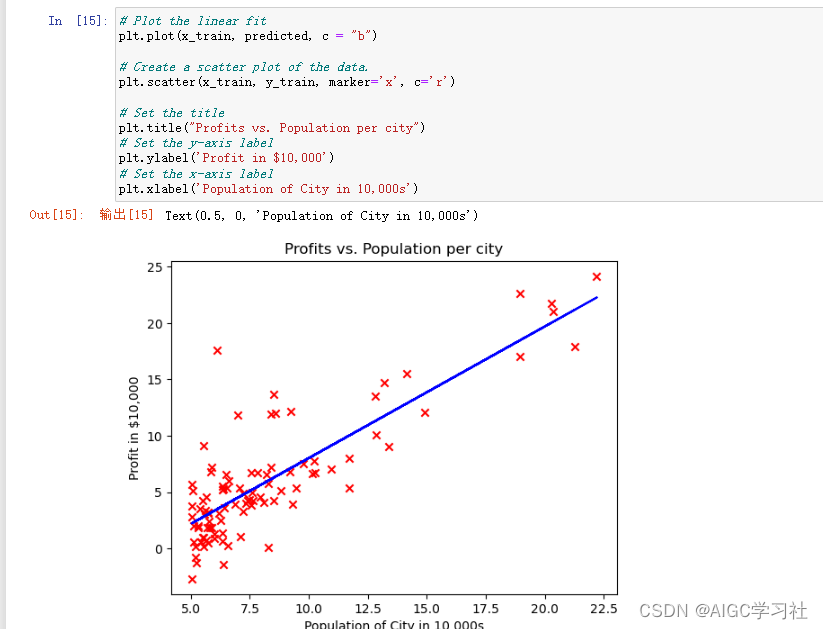
• 为每一行训练样本计算预测值。
• 通过得到的预测值绘画出蓝色线条，拟合数据。
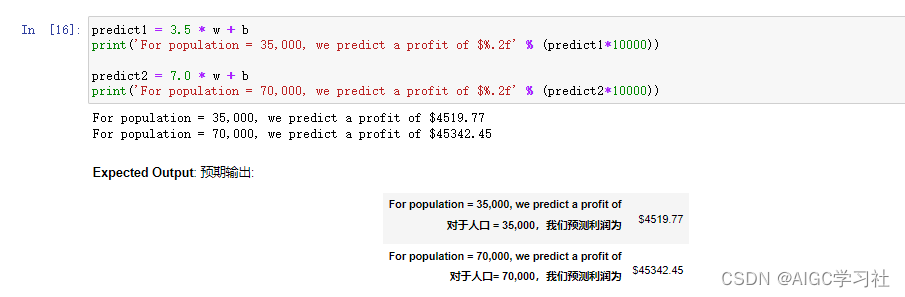
• 具体运用，预测35000人口城市的餐厅利润多少，70000人口城市的餐厅利润多少。

总结

通过实现一元线性回归，我们预测了不同人口城市下的餐厅连锁店的利润。在预测类似的问题时，我们采用线性回归模型，先了解训练集，然后通过训练集数据计算成本函数和梯度下降，然后我们为梯度下降设置迭代次数，得到最优的w，b。通过w，b，我们就可以代入线性回归公式预测了。