Day 27 39. 组合总和 40.组合总和II 131.分割回文串

组合总和

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

所有数字（包括 target）都是正整数。
解集不能包含重复的组合。

示例 1：

输入：candidates = [2,3,6,7], target = 7,
所求解集为： [ [7], [2,2,3] ]

示例 2：

输入：candidates = [2,3,5], target = 8,
所求解集为： [ [2,2,2,2], [2,3,3], [3,5] ]

首先考虑题目中提到的无限制重复选取，那么就一定要去除零的存在，否则将进入死循环；

题目给出1 <= candidates[i] <= 200，说明此处不用担心死循环的问题；

此处依然采取构建树形结构的回溯，可知此时树的深度是由target和sum的值来限定的：

和组合问题最大的区别是每一次取数都是从整个candidates数组取数，这样才保证了题目要求的无限制重复选取；

下面是回溯代码：

	vector<vector<int>>	res;vector<int>	path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex){//sum记录路径总和以确定路径是否满足要求，startIndex防止结果出现重复的组合if(sum >= target){if(sum == target)	res.push_back(path);return;}//终止条件不难理解，sum>=target即不再往下for(int i = startIndex; i < candidates.size(); i++){path.push_back(candidates[i]);sum += candidates[i];backtracking(candidates, target, sum, i);//注意这里不是i+1，因为要满足可取重复元素sum -= candidates[i];path.pop_back();}}

注意此处依然可以进行剪枝操作，如果得到的是一个排序数组，那只要for循环中的下一层的sum。即本层的sum + candidates[i]>target了，就可以直接退出for循环了；即

	for(int i = startIndex; i < candidates.size() && sum + candiates[i] <= target; i++)

整体代码如下：

class Solution {
private:vector<vector<int>>	res;vector<int>	path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex){//sum记录路径总和以确定路径是否满足要求，startIndex防止结果出现重复的组合if(sum >= target){if(sum == target)	res.push_back(path);return;}//终止条件不难理解，sum>=target即不再往下for(int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++){path.push_back(candidates[i]);sum += candidates[i];backtracking(candidates, target, sum, i);sum -= candidates[i];path.pop_back();}}
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {res.clear();path.clear();sort(candidates.begin(), candidates.end()); //剪枝操作要求有序数组backtracking(candidates, target, 0, 0);return res;}
};

组合总和Ⅱ

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：所有数字（包括目标数）都是正整数。解集不能包含重复的组合。

示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:

[[1, 7],[1, 2, 5],[2, 6],[1, 1, 6]
]

示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:

[[1,2,2],[5]
]

和上道题的思路是极为类似的，这道题很明显是数组中可以含有数值相同的元素，但是组合中又不允许出现重复的组合，也就是剪枝需要剪掉所有可能出现重复元素的场景，因为此处去重操作是去除树层里的重复元素，而不是树枝里的重复元素，因为组合允许出现相同的数值；

显而易见，此时若想进行去重操作，原数组一定是一个排序好的数组；

此处举例说明为什么要进行数层剪枝：candidates = [1, 1, 2], target = 3；

所以我们可以使用一个和nums.size()等长的used数组来记录遍历情况，每次遍历之前先检索used数组即可知道此时是否应该进行剪枝操作；

	vector<vector<int>>	res;vector<int>	path;void backtracking(vector<int>& nums, int targetSum, int sum, int startIndex, vector<bool> used){if(sum >= targetSum){//终止条件和上一样if(sum == targetSum)	res.push_back(path);return;}for(int i = startIndex; i < nums.szie() && sum + nums[i] <= target; i++){//剪枝if(i > 0 && nums[i] == nums[i - 1]  && used[i - 1] == false){//剪枝，如果是操作数层是继续下一层循环//此时used[i - 1] == true;则是操作树枝continue;}path.push_back(nums[i]);used[i] = true;sum += nums[i];backtracking(nums, targetSum, sum, i, used);sum -= nums[i];used[i] = false;path.pop_back();}}

不用used数组也可以实现，整体代码如下：

class Solution {
private:vector<vector<int>> res;vector<int> path;void backtracking(vector<int>& nums, int targetSum, int sum, int startIndex/*, vector<bool>& used*/) {if (sum == targetSum) {res.push_back(path);return;}for (int i = startIndex; i < nums.size() && sum + nums[i] <= targetSum; i++) { // 剪枝// if(i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) { // 剪枝，如果是操作数层是继续下一层循环//  把判空条件写在了执行语句后面，找了半个多小时才找到问题，警钟撅烂   // 此时used[i - 1] == true;则是操作树枝//     continue;// }//可以不使用used数组的方式进行树层去重剪枝//此时要求i>startIndex说明至少已经操作过一个元素，不会漏掉组合的可能性，即保证了最左侧树枝可以取到，同时满足了i>0的判定数组下标非负判断if(i > startIndex && nums[i] == nums[i - 1]){continue;}path.push_back(nums[i]);// used[i] = true;sum += nums[i];backtracking(nums, targetSum, sum, i + 1/*, used*/);sum -= nums[i];// used[i] = false;path.pop_back();}}
public:vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {res.clear();path.clear();//vector<bool> used(candidates.size(), false);sort(candidates.begin(), candidates.end()); // 排序backtracking(candidates, target, 0, 0);return res;}
};

分割回文串

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回 s 所有可能的分割方案。

示例: 输入: “aab” 输出: [ [“aa”,“b”], [“a”,“a”,“b”] ]

回文串是一个局部的字符串片段，它在正向和反向读来都保持一致;

组合问题：选取一个a之后，在bcdef中再去选取第二个，选取b之后在cdef中再选取第三个；

切割问题：切割一个a之后，在bcdef中再去切割第二段，切割b之后在cdef中再切割第三段；

所以切割问题可以抽象为和组合问题一样的解决方法；

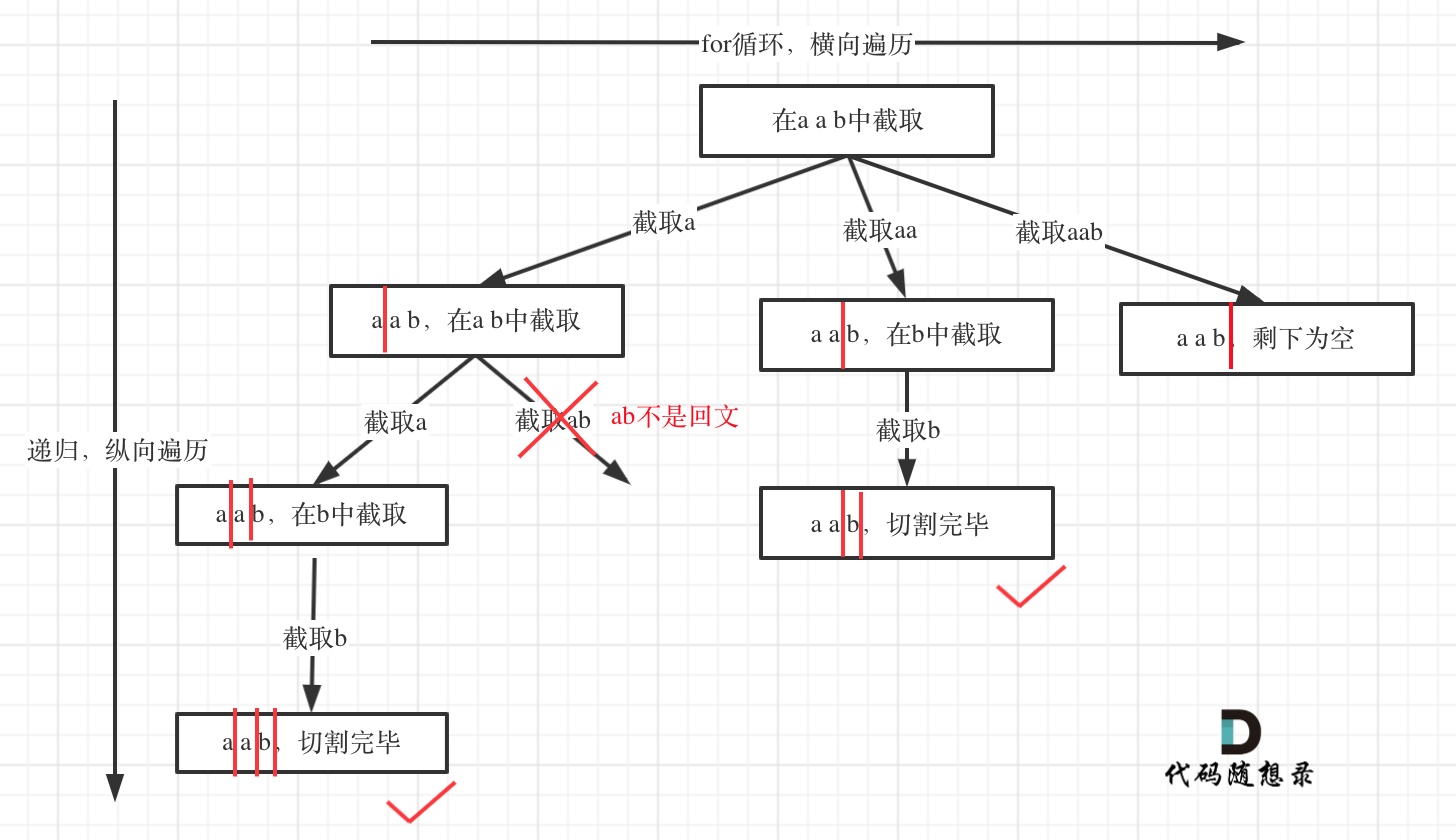
for循环横向遍历，纵向递归当切割线到字符串最后一位的时候即得到一组切割方法；

	vector<string>	path;vector<vector<string>>	res;//回溯函数的参数void backtracking(const string& s, int startIndex){if(startIndex == s.size()){//终止条件，判断回文是否放进单层递归逻辑里res.push_back(path);return;}for(int i = startIndex; i < s.size(); i++){if(isPalindrome2(s, startIndex, i)){//判断是否回文string temp = s.substr(startIndex, i - startIndex + 1);//左闭右闭path.push_back(temp);}//如果不是回文子串则放弃对此字串的搜索else continue;backtracking(s, i + 1);path.pop_back();}}bool isPalindrome1(const string& s, int begin, int end){//首尾遍历判断是否为回文串while(s[begin] == s[end] && begin <= end){begin++;end--;}if(begin >= end)	return true;else return false;}bool isPalindrome2(const string& s, int begin, int end){for(int i = begin, j = end; i < j; i++, j--){if(s[i] != s[j])	return false;}return true;}

整体代码如下：

class Solution {
private:vector<string>	path;vector<vector<string>>	res;//回溯函数的参数void backtracking(const string& s, int startIndex){if(startIndex == s.size()){//终止条件，判断回文是否放进单层递归逻辑里res.push_back(path);return;}for(int i = startIndex; i < s.size(); i++){if(isPalindrome2(s, startIndex, i)){//判断是否回文string temp = s.substr(startIndex, i - startIndex + 1);//左闭右闭path.push_back(temp);}//如果不是回文子串则放弃对此字串的搜索else continue;backtracking(s, i + 1);path.pop_back();}}bool isPalindrome1(const string& s, int begin, int end){//首尾遍历判断是否为回文串while(s[begin] == s[end] && begin <= end){begin++;end--;}if(begin >= end)	return true;else return false;}bool isPalindrome2(const string& s, int begin, int end){for(int i = begin, j = end; i < j; i++, j--){if(s[i] != s[j])	return false;}return true;}
public:vector<vector<string>> partition(string s) {path.clear();res.clear();backtracking(s,0);return res;}
};