标签：树、树形$dp$
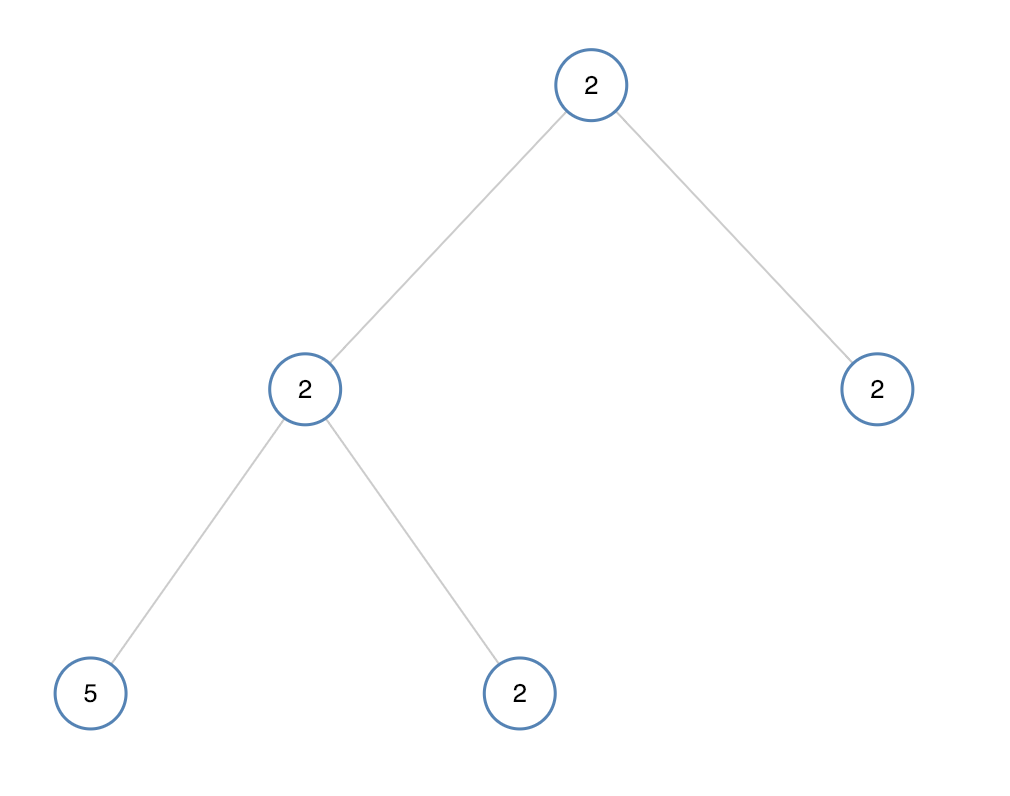
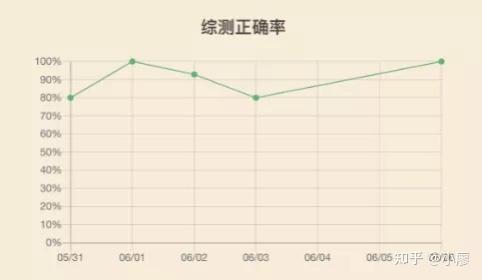
题意：给定一棵$n$个结点的树，$1$号点为这棵树的根。计算这棵树连通子图的个数，答案对$1,000,000,007$取余数。
题解：经典树形$dp$，对于每个节点$u$分两种情况：

dp[u][0]：表示含有以u节点作为根的连通子图个数
dp[u][1]：表示不含有以u节点作为根的连通子图个数

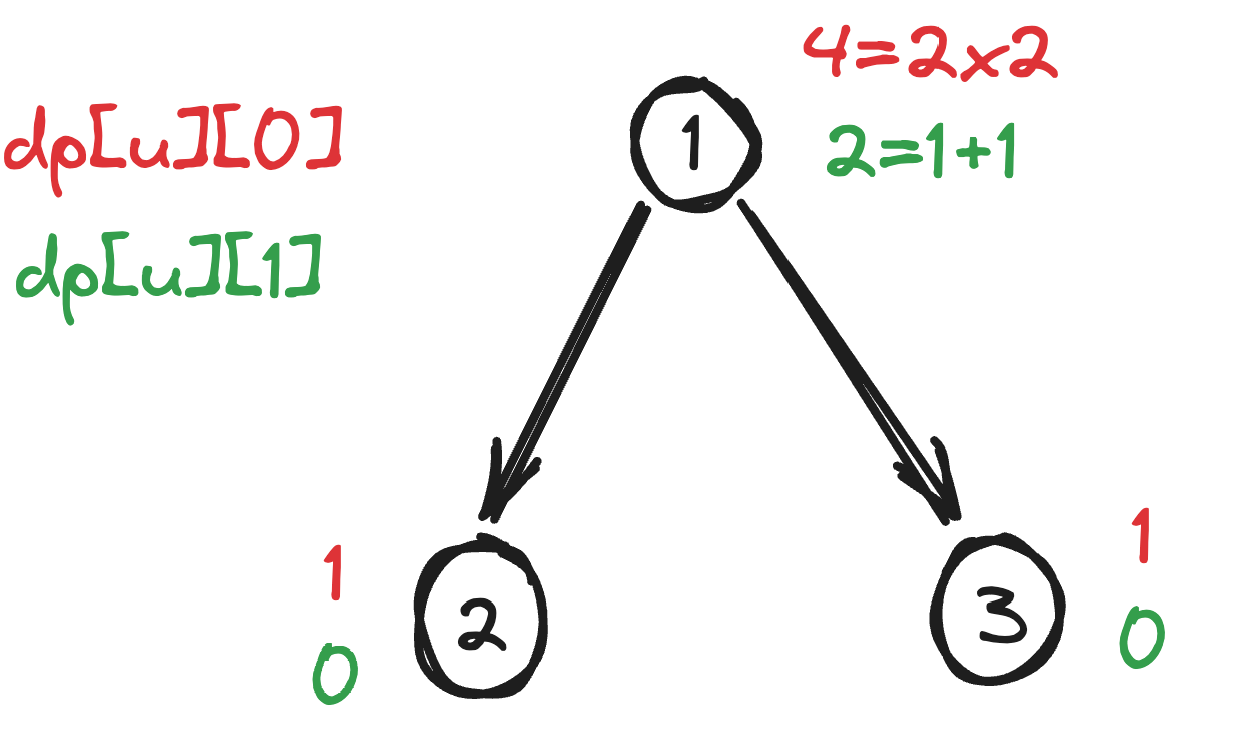
1. 对于节点$u$的每个孩子节点$v$来说，如果把$u$算上去，连通子图的个数要做乘积（乘法原理）
2. 对于节点$u$的每个孩子节点$v$来说，如果不把$u$算上去，连通子图的个数要做相加（加法原理）

可以结合样例和给出的图，自己再推一推，想一想。做法是先把图存进邻接表里面，既然是根节点为$1$，并且给出的都是每个节点的父亲节点，直接存单向边，然后从根节点$1$从上往下遍历树，对应更新$dp[u][0]$和$dp[u][1]$即可。
代码：

#include <bits/stdc++.h>
using namespace std;typedef long long ll;
const ll mod = 1e9 + 7;
vector<ll> e[200005];
ll dp[200005][2];
// dp[u][0]: 含有以u节点作为根的连通子图个数
// dp[u][1]: 不含有以u节点作为根的连通子图个数void dfs(ll u) {dp[u][0] = 1;for (int i = 0; i < e[u].size(); i++) {ll v = e[u][i];dfs(v);dp[u][0] = (dp[u][0] * (dp[v][0] + 1)) % mod;dp[u][1] = (dp[u][1] + dp[v][0] + dp[v][1]) % mod;}
}int main() {ll n, x;cin >> n;for (int i = 2; i <= n; i++) {cin >> x;e[x].push_back(i);}dfs(1);cout << (dp[1][0] + dp[1][1]) % mod << endl;return 0;
}