AcWing 796. 子矩阵的和

题目描述

输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式

第一行包含三个整数 n，m，q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含四个整数 x1,y1,x2,y2，表示一组询问。

输出格式

共 q 行，每行输出一个询问的结果。

数据范围

1≤n,m≤1000,

1≤q≤200000,

1≤x1≤x2≤n1,

1≤y1≤y2≤m1,

−1000≤矩阵内元素的值≤1000

输入样例：

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

输出样例：

17
27
21

思路

C++

#include <iostream>using namespace std;const int N = 1010;
int s[N][N];int main() {int n, m, q;scanf("%d%d%d", &n, &m, &q);for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {int tmp;scanf("%d", &tmp);s[i][j] = s[i][j - 1] + s[i - 1][j] - s[i - 1][j - 1] + tmp;}}while (q--) {int x1, y1, x2, y2;scanf("%d%d%d%d", &x1, &y1, &x2, &y2);printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);}
}

#include <iostream>using namespace std;const int N = 1010;int n, m, q;
int s[N][N];int main() {scanf("%d%d%d", &n, &m, &q);for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)scanf("%d", &s[i][j]);for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];while (q--) {int x1, y1, x2, y2;scanf("%d%d%d%d", &x1, &y1, &x2, &y2);printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);}return 0;
}

Go

package mainimport ("bufio""fmt""os"
)func main() {reader := bufio.NewReader(os.Stdin)var n, m, q intfmt.Fscan(reader, &n, &m, &q)s := make([][]int, n+1)for i := range s {s[i] = make([]int, m+1)}for i := 1; i <= n; i++ {for j := 1; j <= m; j++ {var tmp intfmt.Fscan(reader, &tmp)s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + tmp}}writer := bufio.NewWriter(os.Stdout)defer writer.Flush()for i := 0; i < q; i++ {var x1, y1, x2, y2 intfmt.Fscan(reader, &x1, &y1, &x2, &y2)result := s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1]fmt.Fprintln(writer, result)}
}

模板

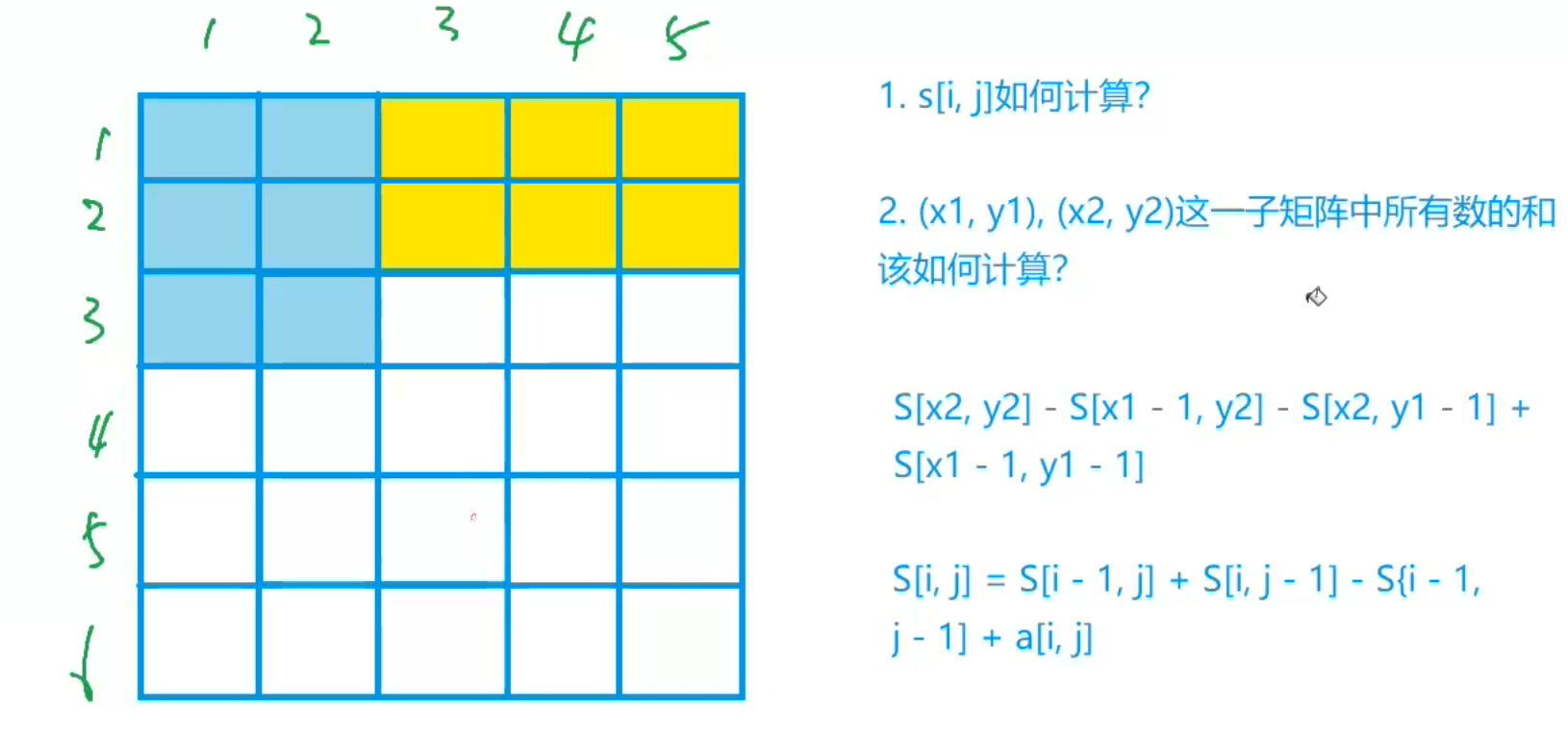
S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]