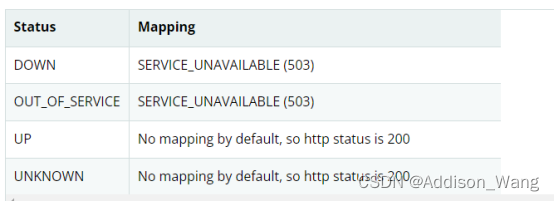
Problem: 48. 旋转图像
文章目录
- 题目描述
- 思路
- 复杂度
- Code
题目描述
思路
1.初始化:首先,我们需要获取矩阵的长度len,这将用于后续的索引计算。
2.外层循环:我们使用一个外层循环for (int i = 0; i < len / 2; i++)来遍历矩阵的每一层。这里的i表示当前层的索引,len / 2是层数(对于一个n x n的矩阵,它有n / 2层)。
3.内层循环:对于每一层,我们使用一个内层循环for (int j = i; j < len - i - 1; j++)来遍历这一层的每一个元素。这里的j表示当前元素在这一层中的位置,len - i - 1是这一层的长度。
4.计算旋转后的位置:对于每一个元素,我们需要计算它在旋转90度后应该在的位置。我们使用int m = len - j - 1和int n = len - i - 1来计算这个位置的行索引和列索引。
5.元素交换:最后,我们交换四个位置的元素:matrix[i][j],matrix[m][i],matrix[n][m],和matrix[j][n]。这四个操作完成了一个环形的旋转。
复杂度
时间复杂度:
O ( n ) O(n) O(n)
空间复杂度:
O ( 1 ) O(1) O(1)
Code
class Solution {/*** Rotate a matrix 90 degrees clockwise** @param matrix Given array*/public void rotate(int[][] matrix) {int len = matrix.length;for (int i = 0; i < len / 2; i++) {for (int j = i; j < len - i - 1; j++) {int m = len - j - 1;int n = len - i - 1;//Exchangeint temp = matrix[i][j];matrix[i][j] = matrix[m][i];matrix[m][i] = matrix[n][m];matrix[n][m] = matrix[j][n];matrix[j][n] = temp;}}}
}








![[Java EE] 多线程(四):线程安全问题(下)](https://img-blog.csdnimg.cn/direct/12d6660fd251483898dba6ebb23a7a0e.png)