目录
- 标量
- 向量
- 矩阵
- 特殊矩阵
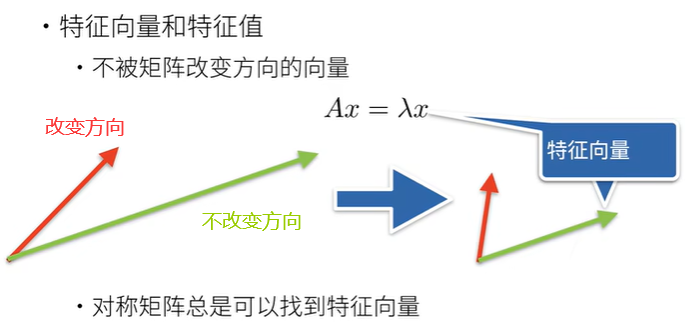
- 特征向量和特征值
- 标量由只有一个元素的张量表示
- 将向量视为标量值组成的列表
- 通过张量的索引来访问任一元素
- 访问张量的长度
- 只有一个轴的张量,形状只有一个元素
- 通过指定两个分量m和n来创建一个形状为m×n的矩阵
- 矩阵的转置
- 对称矩阵的转置逻辑运算
- clone()复制一个有相同形状的张量
- 两个矩阵的按元素乘法称为:哈达玛积⊙
- 计算元素的和
- 表示任意形状张量的元素和
- 参数axis=0求和
- 参数axis=1求和
- axis=[0,1] 必须满足三个维度以上
- 示例说明1
- 示例说明2
- 示例说明3
- 平均值(mean或average)
- 计算总和或均值时保持轴数不变(即维度不丢失)使用keepdim=True
- keepdim=True保持唯一,不丢失求和的维度,然后才能使用广播机制
- 某个轴计算A元素的累积和(即前缀和)
- 点积dot(参数1,参数2)
- 矩阵向量积torch.mv(参数1,参数2)
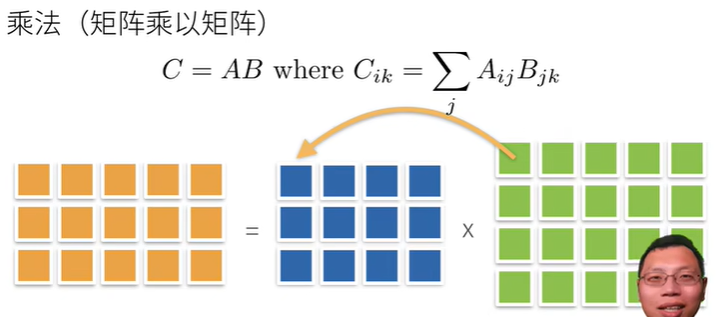
- 矩阵乘法
- norm()函数
- 向量元素的绝对值之和
- F范式:矩阵元素的平方和的平方根
标量

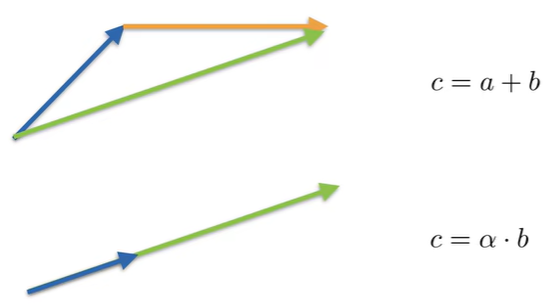
向量

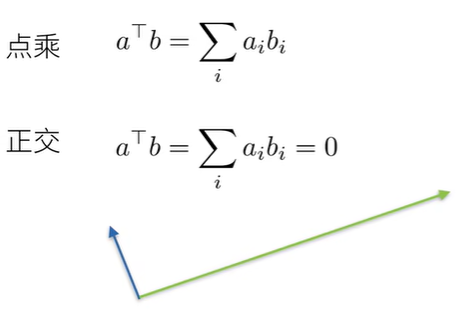
矩阵

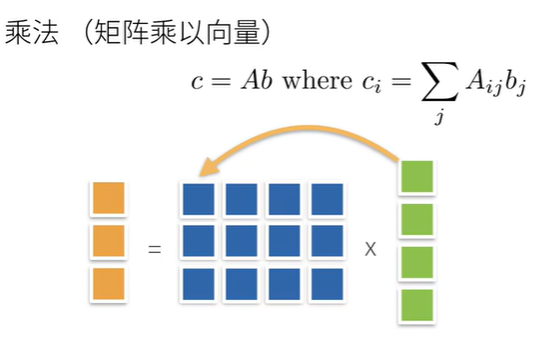

特殊矩阵


特征向量和特征值
标量由只有一个元素的张量表示
import torch
x = torch.tensor([3.0])
y = torch.tensor([2.0])
print(x + y)
print(x * y)
print(x / y)
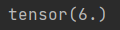
print(x ** y)
结果: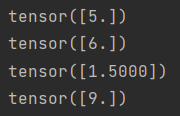
将向量视为标量值组成的列表
import torch
x = torch.arange(4)
print(x)
结果:
通过张量的索引来访问任一元素
import torch
x = torch.arange(4)
print(x[3])
结果: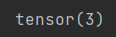
访问张量的长度
import torch
x = torch.arange(4)
print(len(x))
结果:
只有一个轴的张量,形状只有一个元素
import torch
x = torch.arange(4)
print(x.shape)
结果: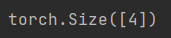
一个长为1的列表
通过指定两个分量m和n来创建一个形状为m×n的矩阵
import torch
A = torch.arange(20).reshape((5, 4))
print(A)
结果: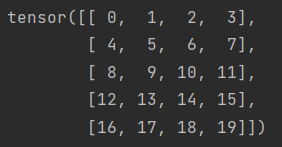
矩阵的转置
import torch
A = torch.arange(20).reshape((5, 4))
print(A.T)
结果: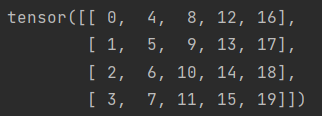
对称矩阵的转置逻辑运算
import torch
B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
print(B == B.T)
结果:
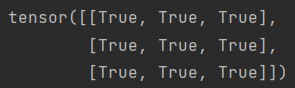
clone()复制一个有相同形状的张量
import torch
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()
print(A)
print(A + B)
结果:
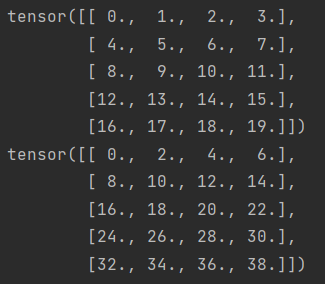
两个矩阵的按元素乘法称为:哈达玛积⊙
import torch
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()
print(A*B)
结果:
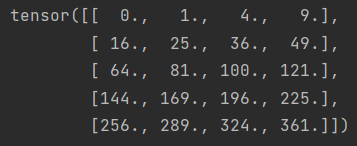
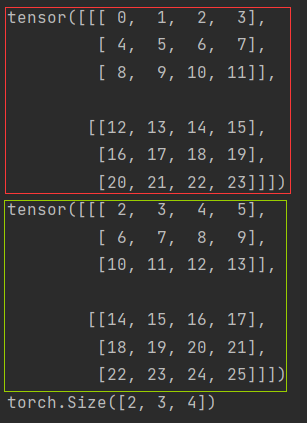
import torch
a = 2 #对矩阵中的每个元素+2
x = torch.arange(24).reshape(2, 3, 4) #reshape第一个参数可以看作是“块”或“层”的数量
print(x)
print(a + x)
print((a * x).shape)
结果:
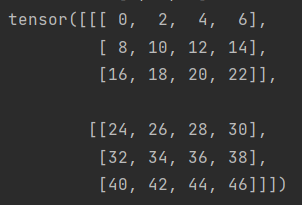
print(a * x)
计算元素的和
import torch
x = torch.arange(4, dtype=torch.float32)
print(x)
print(x.sum())
结果:
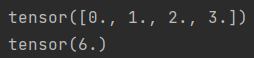
表示任意形状张量的元素和
import torch
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
print(A.shape)
print(A.sum())
结果:
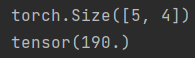
参数axis=0求和
如果是二维则代表沿着行的方向(第一维)进行操作(从上到下)
import torch
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
A_sum_axis0 = A.sum(axis=0)
print(A)
print(A_sum_axis0)
print(A_sum_axis0.shape)
结果:
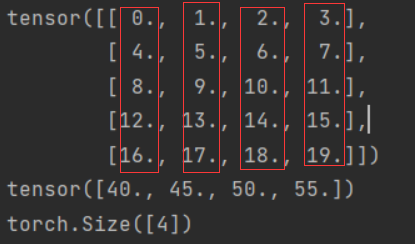
参数axis=1求和
如果是二维则代表沿着列的方向(第二维)进行操作(从左到右)
import torch
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
A_sum_axis1 = A.sum(axis=1)
print(A)
print(A_sum_axis1)
print(A_sum_axis1.shape)
结果:
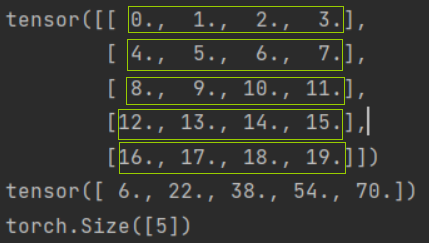
axis=[0,1] 必须满足三个维度以上
对于三维及三维以上的,三个参数分别代表块/层方向(第一维度)、行方向(第二维度)、列方向(第三维度)
此时,就跟二维的有所区别
二维的:axis=0即第一维度------按行方向操作
axis=1即第二维度------按列方向操作
三维即三维以上的:
axis=0 即第一维度------按块/层方向操作
axis=1 即第二维度------按行方向操作
axis=2 即第三维度------按列方向操作
示例说明:
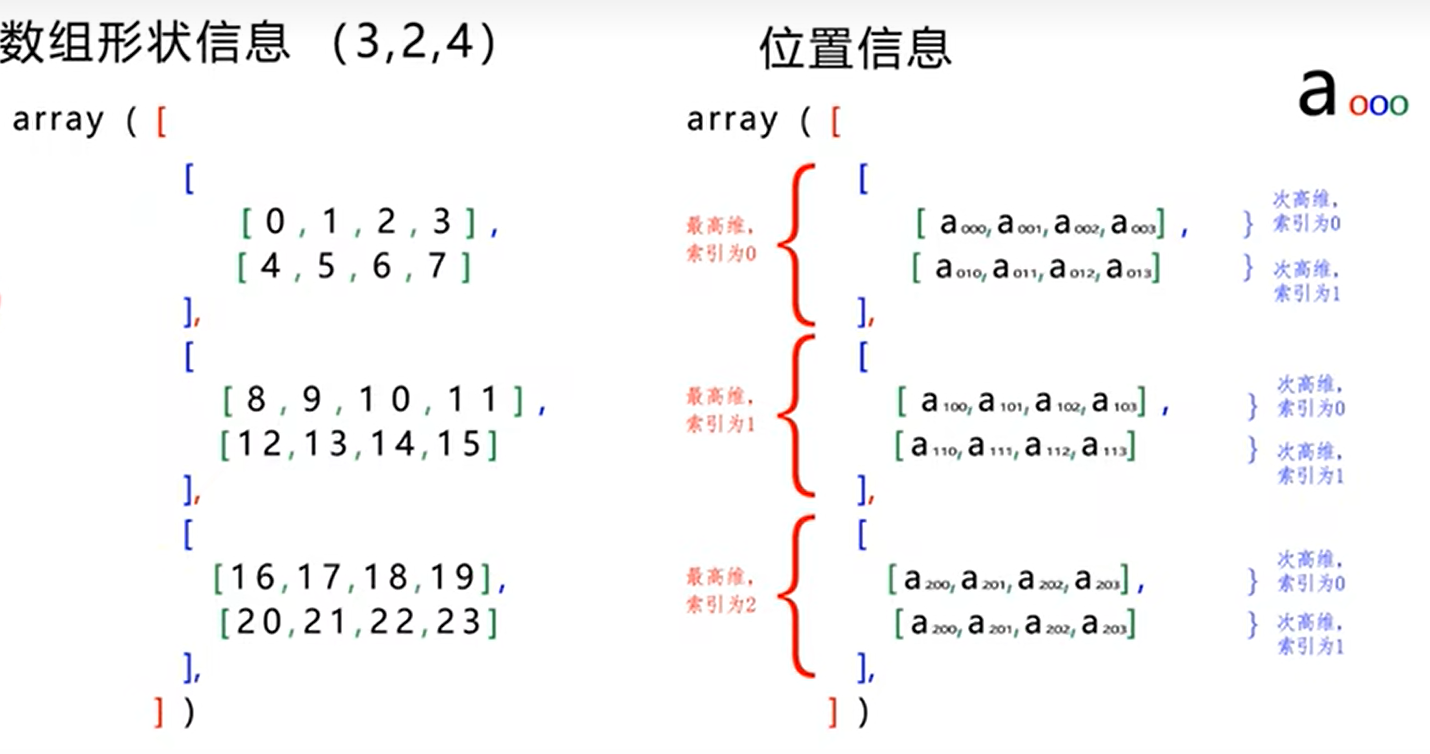
import torch
A = torch.arange(20*2, dtype=torch.float32).reshape(2, 5, 4)
print(A)
print(A.sum(axis=[0, 1]))
结果:
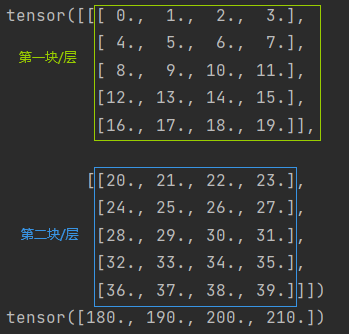


然后,第一层和第二层求和可得:

示例说明1
import torch
a = torch.arange(20).reshape((5, 4))
print(a.shape)
显示:
这里我们使用axis=0沿行方向求和(会丢失第一维度):
import torch
a = torch.arange(20).reshape((5, 4))
print(a.sum(axis=0).shape)
结果:
这里我们使用axis=1沿列方向求和(会丢失第二维度):
import torch
a = torch.arange(20).reshape((5, 4))
print(a.sum(axis=1).shape)
结果:
示例说明2
import torch
a = torch.arange(40).reshape((2, 5, 4))
print(a.shape)
显示:
这里我们使用axis=0沿块/层方向求和(会丢失第一维度):
import torch
a = torch.arange(40).reshape((2, 5, 4))
print(a.sum(axis=0).shape)
结果:
这里我们使用axis=1沿行方向求和(会丢失第二维度):
import torch
a = torch.arange(40).reshape((2, 5, 4))
print(a.sum(axis=1).shape)
结果:
这里我们使用axis=2沿列方向求和(会丢失第三维度):
import torch
a = torch.arange(40).reshape((2, 5, 4))
print(a.sum(axis=2).shape)
结果:
这里我们使用axis=[1, 2]沿行和列方向求和(会丢失第二、三维度):
import torch
a = torch.arange(40).reshape((2, 5, 4))
print(a.sum(axis=[1, 2]).shape)
结果: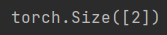
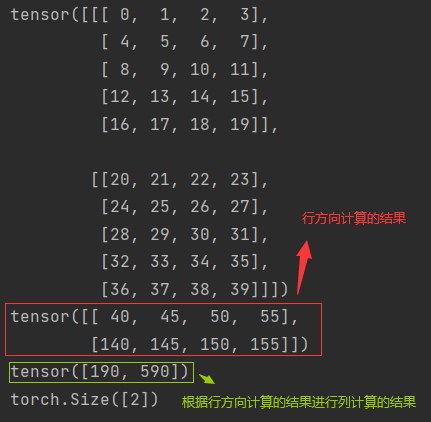
这里我们可以发现是先按照行方向求和计算,之后根据行方向计算的结果进行列方向求和计算。
import torch
a = torch.arange(40).reshape((2, 5, 4))
print(a)
print(a.sum(axis=1))
print(a.sum(axis=[1, 2]))
print(a.sum(axis=[1, 2]).shape)
结果:
示例说明3
keepdim=True使其不丢失维度,将维度变为1
import torch
a = torch.arange(40).reshape((2, 5, 4))
print(a.sum(axis=1, keepdims=True).shape)
结果:
import torch
a = torch.arange(40).reshape((2, 5, 4))
print(a.sum(axis=[1, 2], keepdims=True).shape)
结果:
平均值(mean或average)
import torch
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
print(A.mean())
print(A.sum()/A.numel())
结果:
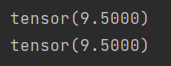
import torch
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
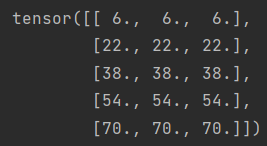
print(A)
print(A.mean(axis=0))
结果:
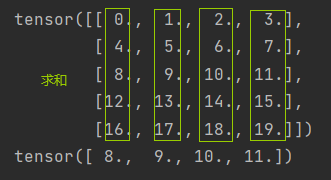
import torch
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
print(A)
print(A.sum(axis=0)/A.shape[0]) #求和的那个维度丢掉了,即按行方向的维度丢掉了
结果:
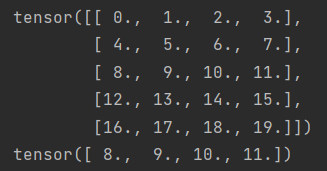
A.shape[0]表示第一个维度(行方向)的元素数
所以用A.shape[1]测试一下是不是元素数
import torch
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
print(A)
print(A.sum(axis=1)/A.shape[1]) #求和的那个维度丢掉了,即按列方向的维度丢掉了
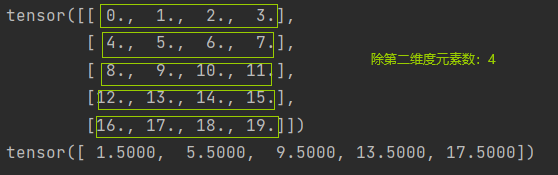
计算总和或均值时保持轴数不变(即维度不丢失)使用keepdim=True
import torch
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
sum_A = A.sum(axis=1, keepdim=True)
print(sum_A)
结果:
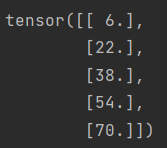
当调用.sum()方法(或类似的聚合方法,如.mean()、.max()等)时,你可以选择是否保持被聚合维度的形状。keepdim=True是一个参数,当设置为True时,它会使得聚合操作后的张量在被聚合的维度上仍然保持一个大小为1的维度,而不是完全去除这个维度。
keepdim=True保持唯一,不丢失求和的维度,然后才能使用广播机制
import torch
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
sum_A = A.sum(axis=1, keepdim=True)
print(A)
print(sum_A)
print(A/sum_A)
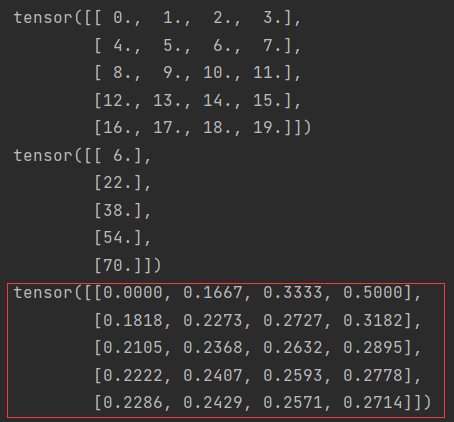
某个轴计算A元素的累积和(即前缀和)
累积和的意思是,对于每个位置,你会将该位置及其之前所有位置上的元素相加。第一个位置的元素保持不变(因为没有之前的元素可以相加),之后的每个位置的元素都是它自身和它之前所有元素的和。
import torch
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
print(A.cumsum(axis=0))
结果:
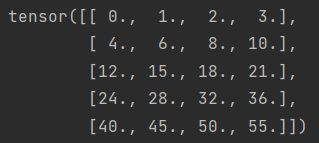
点积dot(参数1,参数2)
torch.dot只能对一维向量做点积
import torch
x = torch.arange(4, dtype=torch.float32)
print(x)
y = torch.ones(4, dtype=torch.float32)
print(y)
print(torch.dot(x, y))
结果:
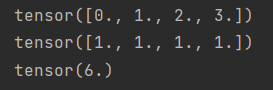
矩阵向量积torch.mv(参数1,参数2)

A是一个m×n的矩阵,x是一个n×1的一列,所以得到一个m的列向量。
m列中第i个元素是点积 a i T a_i^T aiTx
import torch
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
x = torch.arange(4, dtype=torch.float32)
print(A.shape)
print(x.shape)
print(torch.mv(A, x))
结果:

矩阵乘法
矩阵乘法可以看作执行n次矩阵的向量积,然后拼接在一块,形成一个m×n的矩阵。
A:m×q的矩阵
B:q×n的矩阵
AB:m×n的矩阵
import torch
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = torch.ones(4, 3)
print(torch.mm(A, B))
结果:
norm()函数
第二范数是向量元素平方和的平方根
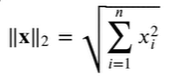
import torch
u = torch.tensor([3.0, -4.0])
print(torch.norm(u))
结果: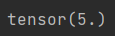
向量元素的绝对值之和
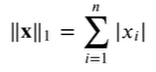
import torch
u = torch.tensor([3.0, -4.0])
print(torch.abs(u).sum())
结果: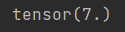
F范式:矩阵元素的平方和的平方根
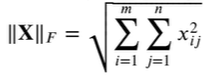
import torch
print(torch.norm(torch.ones((4, 9))))
结果: