斐波那契数列

感谢大佬的光临各位，希望和大家一起进步，望得到你的三连，互三支持，一起进步

个人主页：LaNzikinh-CSDN博客

收入专栏:初阶数据结构_LaNzikinh篮子的博客-CSDN博客

文章目录

前言
一.斐波那契数
二.改循环
三.尾递归
总结

前言

很多人都对递归有了解，但是为尾递归很少，所以这次来专门讲一讲关于尾递归的一些问题。

一.斐波那契数

斐波那契数列（Fibonacci sequence），也称之为黄金分割数列，由意大利数学家列昂纳多・斐波那契（Leonardo Fibonacci）提出。斐波那契数列指的是这样的一个数列：1、1、2、3、5、8、13、21、34、……，这个数列从第 3 项开始，每一项都等于前面两项之和。

那么如何用代码实现斐波那契数呢？

我们通常就是想到用递归的方法，因为这个也是最常见的方法，只要利用函数递归就可以直接使用，思想也很容易去想。

long long Fid(int n)
{if (n <= 2)return 1;elsereturn Fid(n - 1) + Fid(n - 2);
}int main()
{int n = 0;int ret = 0;scanf_s("%d", &n);ret = Fid(n, 1, 1);printf("%d\n", ret);return 0;return 0;
}

但是存在问题，我们自己运行的时候也会发现这些问题，就是当数字大的时候就运行不了，非常的缓慢，那是因为递归多次调用函数，导致的栈溢出，所以我们改怎么修改代码呢？之前我们在改排序的时候也将递归改为非递归的形式，之前我们说过递归改非递归有两种改法，一种是改循环，还有一种就是通过数据结构来转换，我们之前的归并排序非递归就是通过改循环，这次就是通过栈，去搭建。但是这次我们不用数据结构去解决，而是用一种特殊的方法，尾递归

二.改循环

我们先来讲一下最基本的该法，也是我们都清楚的改法，改循坏内部

long long Fid(int n)
{long long f1 = 1;long long f2 = 1;long long f3 = 0;for (int i = 3; i <= n; i++){f3 = f1 + f2;f1 = f2;f2 = f3;}return f3;}int main()
{int n = 0;long long ret = 0;scanf_s("%d", &n);ret = Fid(n);printf("%lld\n", ret);return 0;
}

注意要开long long 因为在后面斐波那契数会越来越大，int很有可能不够用，所以我们就要用long long型来使用

三.尾递归

什么是尾递归

如果一个函数中所有递归形式的调用都出现在函数的末尾，我们称这个递归函数是尾递归的。因为在一些题目的做法中，我们可以发现递归的使用有局限性，有时候会占用相当大的空间。比如斐波那契问题，代码很容易用递归去写，但是浪费了大量的内存，一个数会重复计算多次，所以我们来使用尾递归。这里引用一个我看别人说的一句话，我认为非常对普通递归的结果是返回值，尾递归的结果是参数。完全可以这样理解。

尾递归的优化原理

尾递归优化的概念尾递归是指递归调用出现在函数体的最后，并且是返回值的一部分。它是一种特殊的递归形式，不会在回归过程中做其他操作或表达式的计算。尾调用优化尾调用是尾递归优化的基础。尾调用是指函数调用出现在调用者函数的最后，并且该调用的返回值直接被当前函数返回。尾调用优化的目的是将递归调用转化为尾调用，从而减少函数调用栈的使用。通过尾调用优化，实现函数的尾递归优化，可以避免递归调用带来的栈溢出问题。

然后我们来用尾递归的思路来实现一下斐波那契数的非递归做法

这里跟普通的相比也是多传两个参数，因为最开始的两个数都是1，我们必须提前知道，其实做法和普通方法的思维是一致的也是相加，但是最后需要用这个b来表示出来，用逗号表达式的这个知识和函数传参.

int Fib(int n, int a, int b) 
{if (n < 3){return b;}elsereturn Fib(n - 1, b, a + b);
}

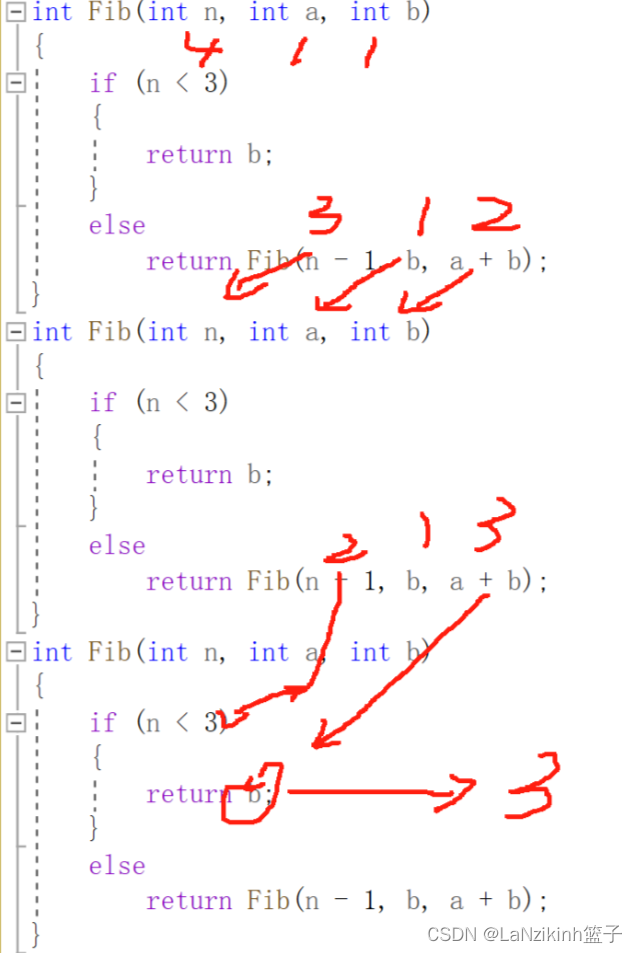
这是我以前写的代码，我们现在来优化一下

long long Fib(int n, long long a, long long b)
{if (n < 3){return b;}elsereturn Fib(n - 1, b, a + b);
}int main()
{int n = 0;long long ret = 0;scanf_s("%d", &n);ret = Fib(n,1,1);printf("%lld\n", ret);return 0;
}