目录
什么是二叉搜索树
二叉搜索树的特性
(1)顺序性
(2)局限性
二叉搜索树的应用
二叉搜索树的操作
(1)查找节点
(2)插入节点
(3)删除节点
(4)中序遍历
什么是二叉搜索树
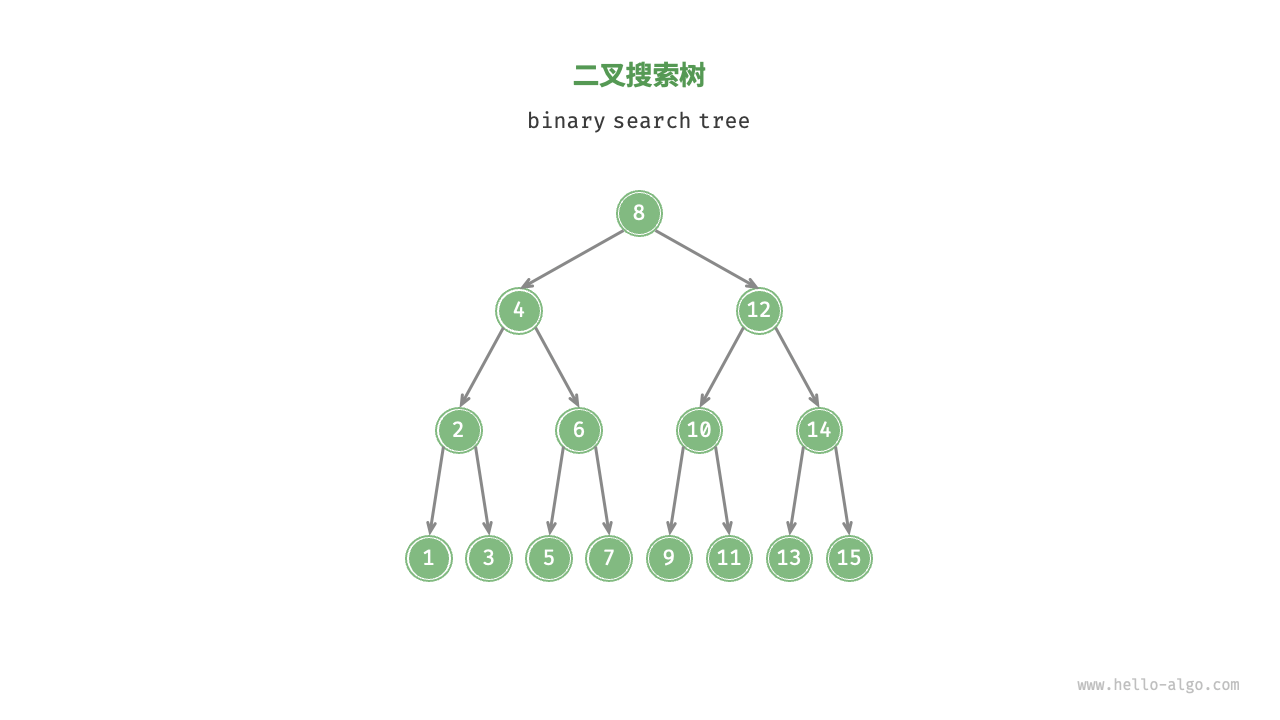
如图所示,二叉搜索树(binary search tree)满足以下条件。
- 对于根节点,左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值。
- 任意节点的左、右子树也是二叉搜索树,即同样满足条件
1.。
二分搜索树有着高效的插入、删除、查询操作。
平均时间的时间复杂度为 O(log n),最差情况为 O(n)。二分搜索树与堆不同,不一定是完全二叉树,底层不容易直接用数组表示故采用链表来实现二分搜索树。只有在高频添加、低频查找删除数据的场景下,数组比二叉搜索树的效率更高。
| 查找元素 | 插入元素 | 删除元素 | |
|---|---|---|---|
| 普通数组 | O(n) | O(n) | O(n) |
| 顺序数组 | O(logn) | O(n) | O(n) |
| 二分搜索树 | O(logn) | O(logn) | O(logn) |
二叉搜索树的特性
(1)顺序性
二分搜索树可以当做查找表的一种实现。
我们使用二分搜索树的目的是通过查找 key 马上得到 value。minimum、maximum、successor(后继)、predecessor(前驱)、floor(地板)、ceil(天花板、rank(排名第几的元素)、select(排名第n的元素是谁)这些都是二分搜索树顺序性的表现。
(2)局限性
二分搜索树在时间性能上是具有局限性的。
在理想情况下,二叉搜索树是“平衡”的,这样就可以在 log𝑛 轮循环内查找任意节点。
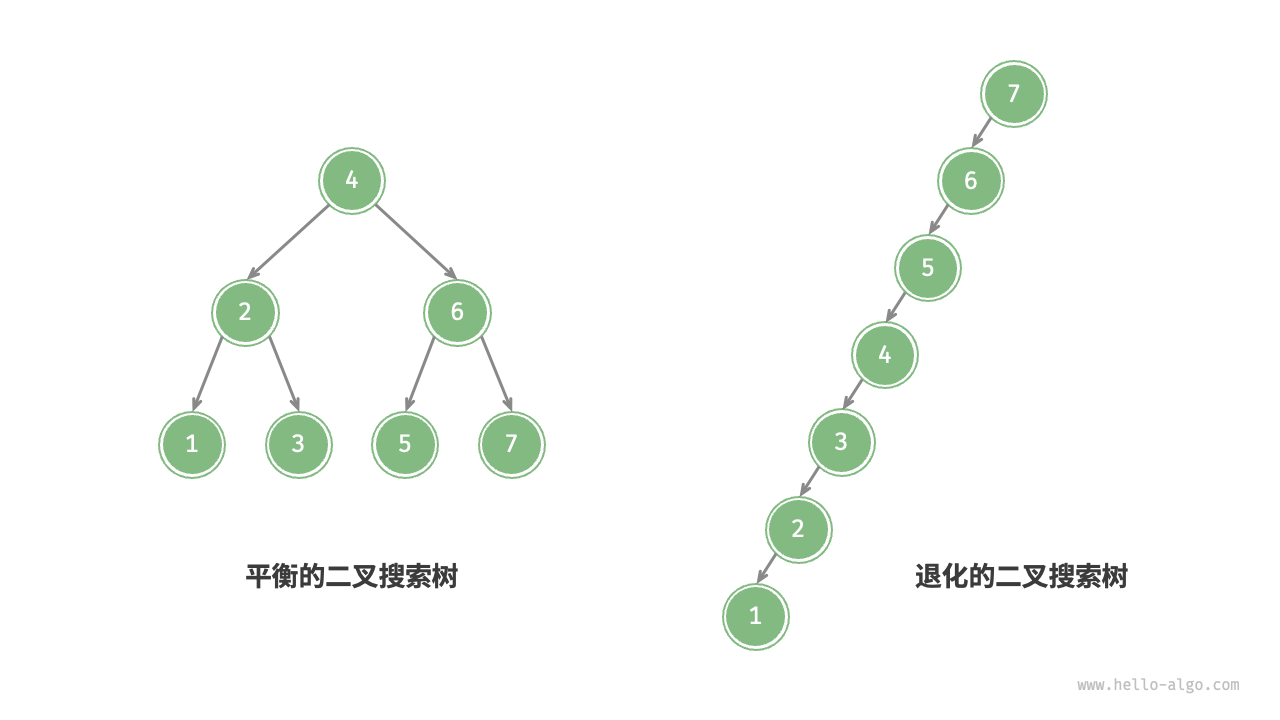
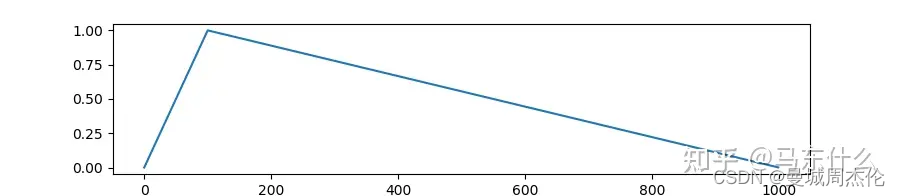
然而,如果我们在二叉搜索树中不断地插入和删除节点,可能导致二叉树退化为如图所示的链表,相应的,二叉搜索树的查找操作是和这棵树的高度相关的,而此时这颗树的高度就是这颗树的节点数 n,这时各种操作的时间复杂度也会退化为 𝑂(𝑛) 。
二叉搜索树的应用
- 用作系统中的多级索引,实现高效的查找、插入、删除操作。
- 作为某些搜索算法的底层数据结构。
- 用于存储数据流,以保持其有序状态
二叉搜索树的操作
(1)查找节点
给定目标节点值 num ,可以根据二叉搜索树的性质来查找。如图 7-17 所示,我们声明一个节点 cur ,从二叉树的根节点 root 出发,循环比较节点值 cur.val 和 num 之间的大小关系。
- 若
cur.val < num,说明目标节点在cur的右子树中,因此执行cur = cur.right。 - 若
cur.val > num,说明目标节点在cur的左子树中,因此执行cur = cur.left。 - 若
cur.val = num,说明找到目标节点,跳出循环并返回该节点。
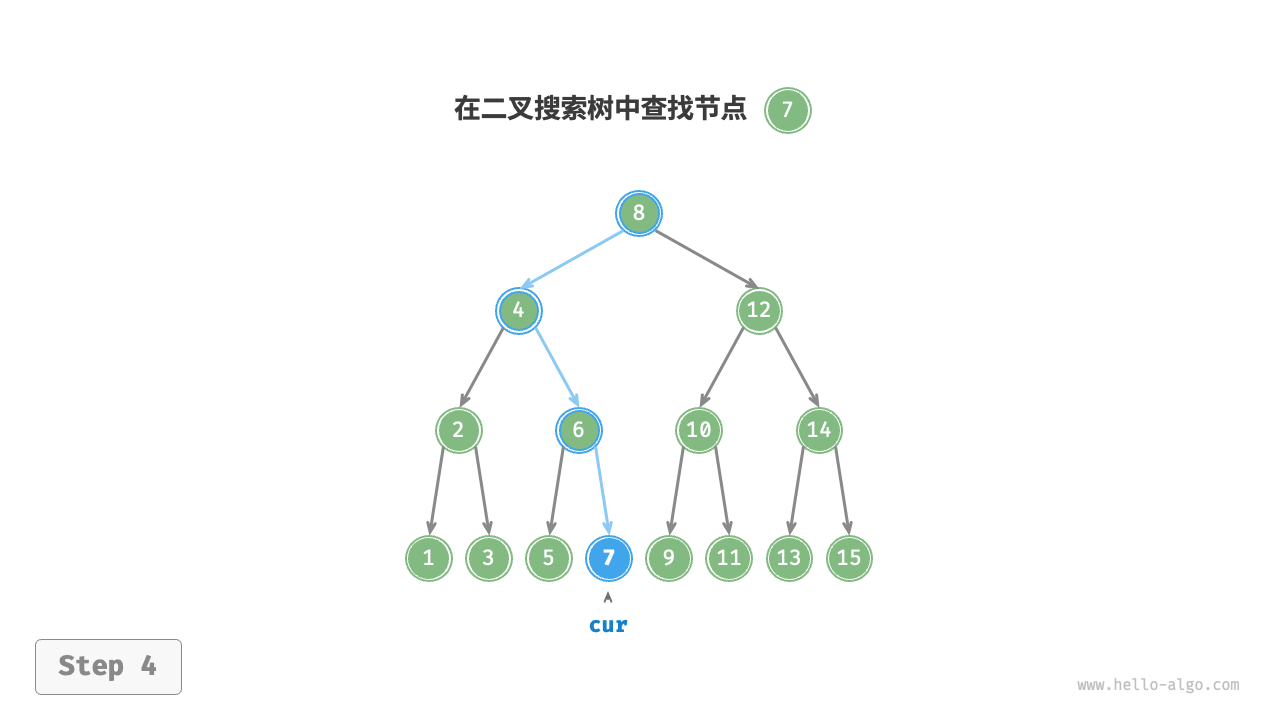
二叉搜索树的查找操作与二分查找算法的工作原理一致,都是每轮排除一半情况。循环次数最多为二叉树的高度,当二叉树平衡时,使用 𝑂(log𝑛) 时间。示例代码如下:
/* 查找节点 */
TreeNode *search(BinarySearchTree *bst, int num) {TreeNode *cur = bst->root;// 循环查找,越过叶节点后跳出while (cur != NULL) {if (cur->val < num) {// 目标节点在 cur 的右子树中cur = cur->right;} else if (cur->val > num) {// 目标节点在 cur 的左子树中cur = cur->left;} else {// 找到目标节点,跳出循环break;}}// 返回目标节点return cur;
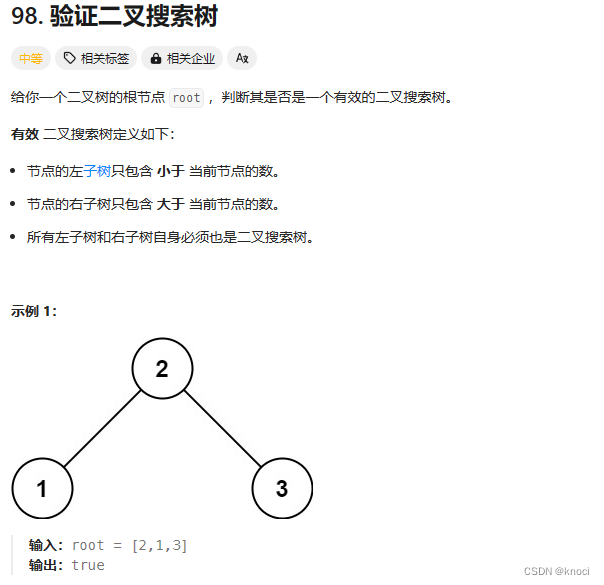
}通过查找节点的方法,我们可以完成98. 验证二叉搜索树 - 力扣(LeetCode)
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/
bool isValidBSTHelper(struct TreeNode* root, long min_val, long max_val) {// 如果根节点为空,直接返回 true,因为空树也是 BSTif (root == NULL) {return true;}// 检查当前节点值是否在范围内if (root->val <= min_val || root->val >= max_val) {return false;}// 递归检查左右子树,更新范围return isValidBSTHelper(root->left, min_val, root->val) && isValidBSTHelper(root->right, root->val, max_val);
}bool isValidBST(struct TreeNode* root) {// 使用 long 类型的最小值和最大值作为初始范围return isValidBSTHelper(root, LONG_MIN, LONG_MAX);
}(2)插入节点
给定一个待插入元素 num ,为了保持二叉搜索树“左子树 < 根节点 < 右子树”的性质,插入操作流程如图所示。
- 查找插入位置:与查找操作相似,从根节点出发,根据当前节点值和
num的大小关系循环向下搜索,直到越过叶节点(遍历至None)时跳出循环。 - 在该位置插入节点:初始化节点
num,将该节点置于None的位置。
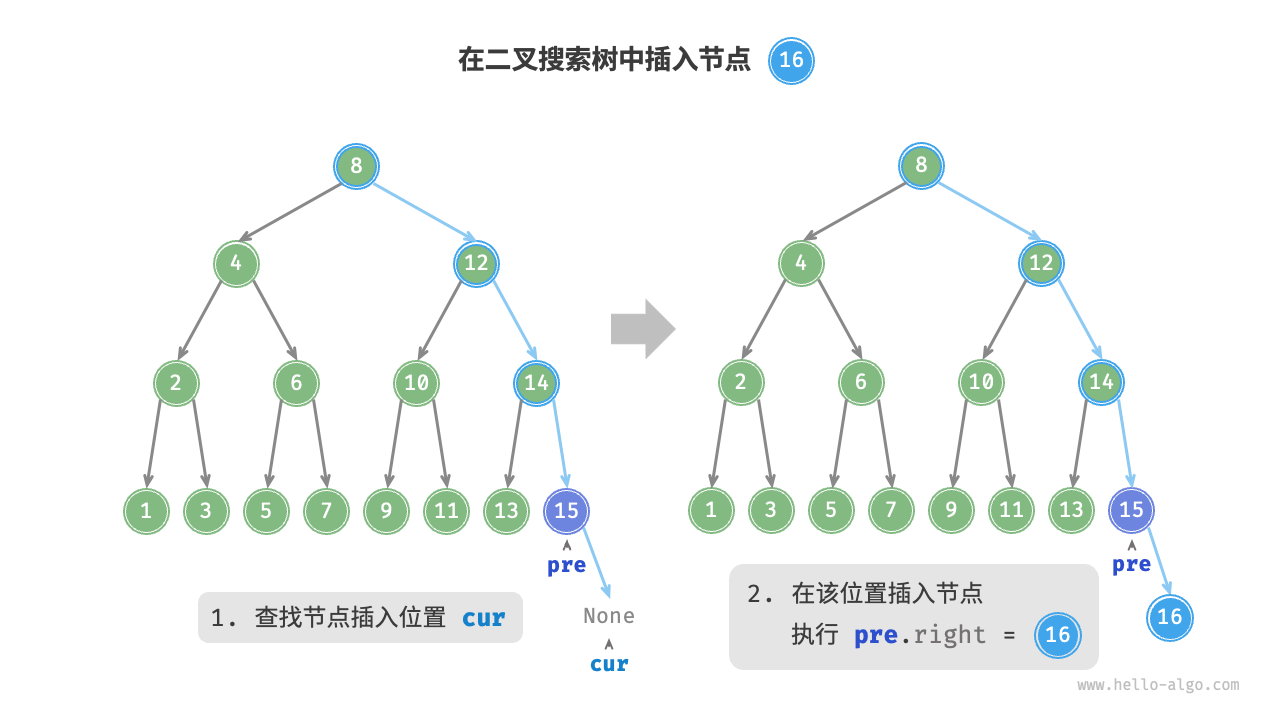
在代码实现中,需要注意以下两点。
- 二叉搜索树不允许存在重复节点,否则将违反其定义。因此,若待插入节点在树中已存在,则不执行插入,直接返回。
- 为了实现插入节点,我们需要借助节点
pre保存上一轮循环的节点。这样在遍历至None时,我们可以获取到其父节点,从而完成节点插入操作。
代码范例如下,与查找节点相同,插入节点使用 𝑂(log𝑛) 时间。
/* 插入节点 */
void insert(BinarySearchTree *bst, int num) {// 若树为空,则初始化根节点if (bst->root == NULL) {bst->root = newTreeNode(num);return;}TreeNode *cur = bst->root, *pre = NULL;// 循环查找,越过叶节点后跳出while (cur != NULL) {// 找到重复节点,直接返回if (cur->val == num) {return;}pre = cur;if (cur->val < num) {// 插入位置在 cur 的右子树中cur = cur->right;} else {// 插入位置在 cur 的左子树中cur = cur->left;}}// 插入节点TreeNode *node = newTreeNode(num);if (pre->val < num) {pre->right = node;} else {pre->left = node;}
}通过插入节点的方法,我们可以完成701. 二叉搜索树中的插入操作 - 力扣(LeetCode)

struct TreeNode* createTreeNode(int val) {struct TreeNode* ret = malloc(sizeof(struct TreeNode));// 设置节点值ret->val = val;// 左右子节点为空ret->left = ret->right = NULL;// 返回新创建的节点return ret;
}struct TreeNode* insertIntoBST(struct TreeNode* root, int val) {// 如果根节点为空,直接将新节点作为根节点返回if (root == NULL) {root = createTreeNode(val);return root;}// 定义游标节点为根节点struct TreeNode* pos = root;// 循环查找插入位置while (pos != NULL) {// 如果 val 小于当前节点值if (val < pos->val) {// 如果当前节点的左子节点为空,将新节点插入左子节点位置if (pos->left == NULL) {pos->left = createTreeNode(val);break;} else {// 否则继续向左子树查找插入位置pos = pos->left;}} else {// 如果 val 大于等于当前节点值// 如果当前节点的右子节点为空,将新节点插入右子节点位置if (pos->right == NULL) {pos->right = createTreeNode(val);break;} else {// 否则继续向右子树查找插入位置pos = pos->right;}}}// 返回根节点return root;
}(3)删除节点
先在二叉树中查找到目标节点,再将其删除。与插入节点类似,我们需要保证在删除操作完成后,二叉搜索树的“左子树 < 根节点 < 右子树”的性质仍然满足。因此,我们根据目标节点的子节点数量,分 0、1 和 2 三种情况,执行对应的删除节点操作。
如图所示,当待删除节点的度为 0 时,表示该节点是叶节点,可以直接删除。
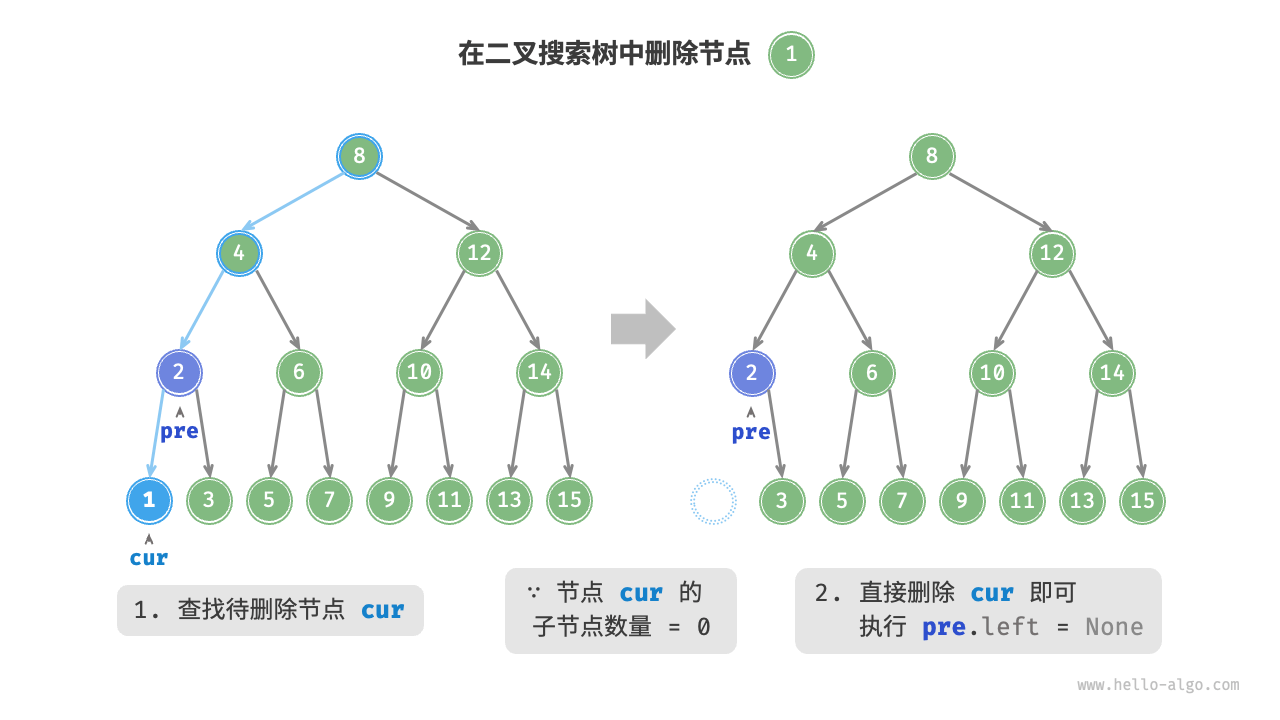
如下图所示,当待删除节点的度为 1 时,将待删除节点替换为其子节点即可。
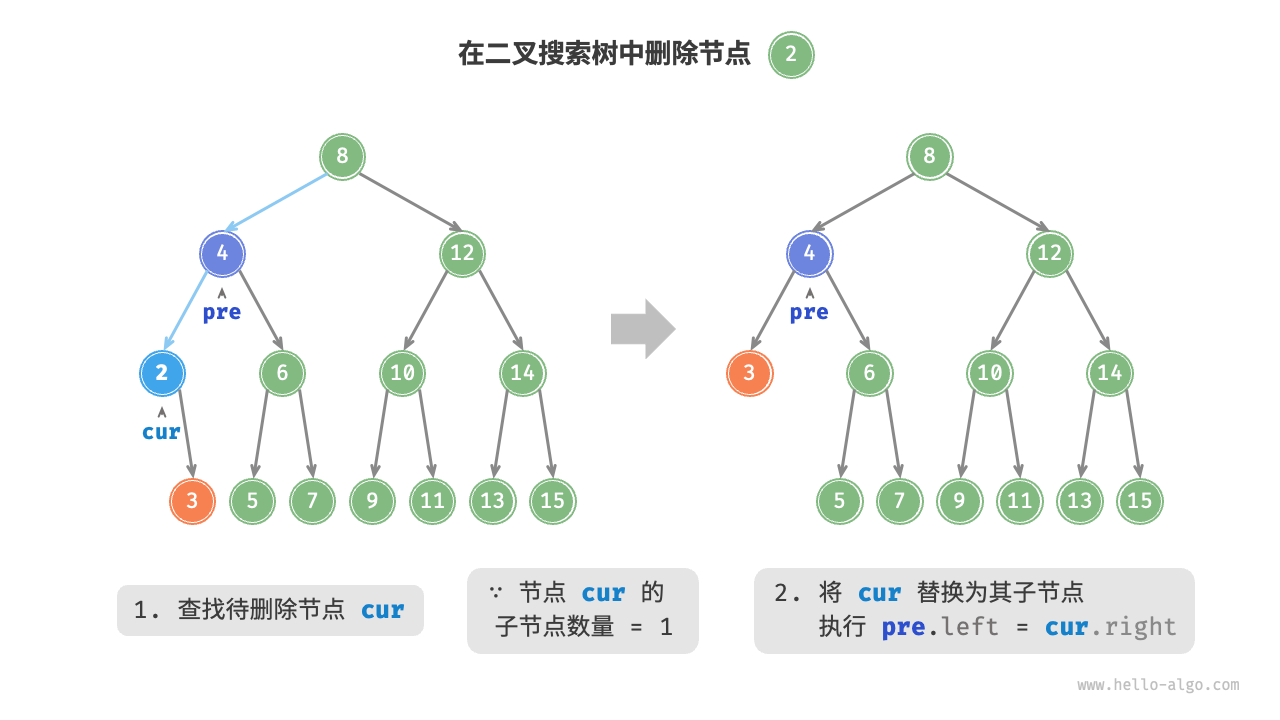
当待删除节点的度为 2 时,我们无法直接删除它,而需要使用一个节点替换该节点。由于要保持二叉搜索树“左子树 < 根节点 < 右子树”的性质,因此这个节点可以是右子树的最小节点或左子树的最大节点。
假设我们选择右子树的最小节点(中序遍历的下一个节点),则删除操作流程如下图所示。
- 找到待删除节点在“中序遍历序列”中的下一个节点,记为
tmp。 - 用
tmp的值覆盖待删除节点的值,并在树中递归删除节点tmp。
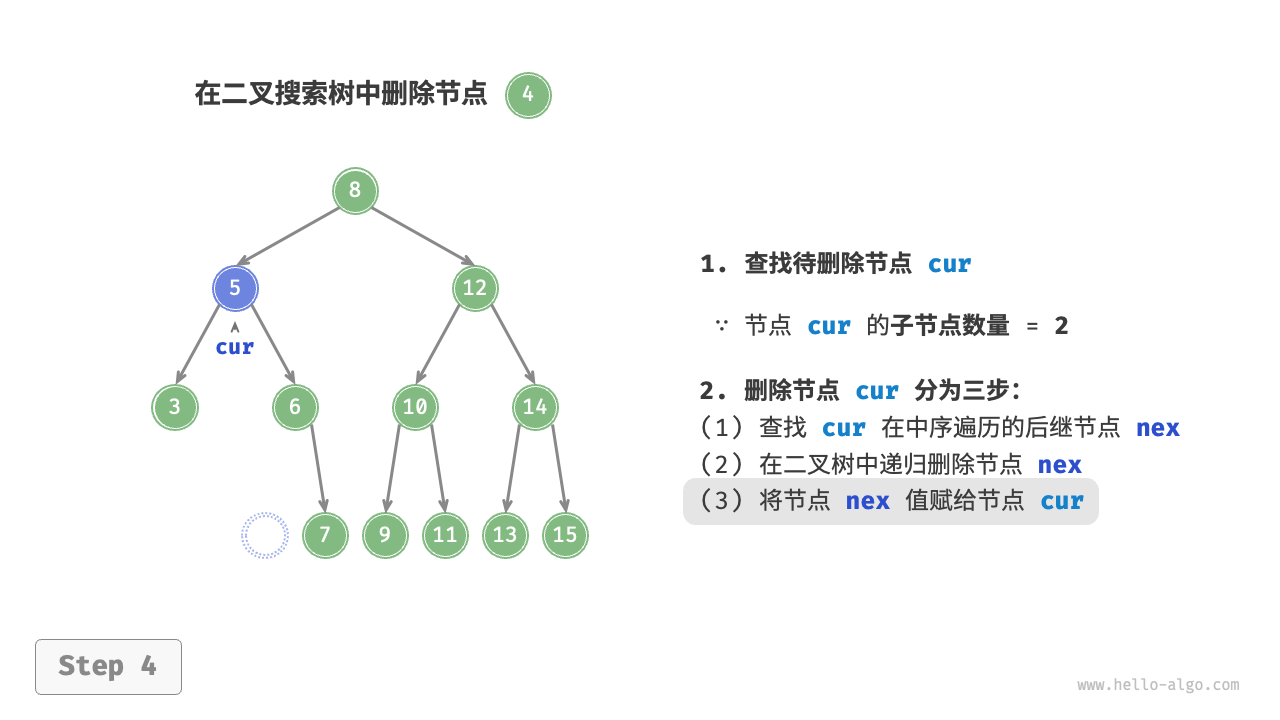
删除节点操作同样使用 𝑂(log𝑛) 时间,其中查找待删除节点需要 𝑂(log𝑛) 时间,获取中序遍历后继节点需要 𝑂(log𝑛) 时间。示例代码如下:
/* 删除节点 */
// 由于引入了 stdio.h ,此处无法使用 remove 关键词
void removeItem(BinarySearchTree *bst, int num) {// 若树为空,直接提前返回if (bst->root == NULL)return;TreeNode *cur = bst->root, *pre = NULL;// 循环查找,越过叶节点后跳出while (cur != NULL) {// 找到待删除节点,跳出循环if (cur->val == num)break;pre = cur;if (cur->val < num) {// 待删除节点在 root 的右子树中cur = cur->right;} else {// 待删除节点在 root 的左子树中cur = cur->left;}}// 若无待删除节点,则直接返回if (cur == NULL)return;// 判断待删除节点是否存在子节点if (cur->left == NULL || cur->right == NULL) {/* 子节点数量 = 0 or 1 */// 当子节点数量 = 0 / 1 时, child = nullptr / 该子节点TreeNode *child = cur->left != NULL ? cur->left : cur->right;// 删除节点 curif (pre->left == cur) {pre->left = child;} else {pre->right = child;}// 释放内存free(cur);} else {/* 子节点数量 = 2 */// 获取中序遍历中 cur 的下一个节点TreeNode *tmp = cur->right;while (tmp->left != NULL) {tmp = tmp->left;}int tmpVal = tmp->val;// 递归删除节点 tmpremoveItem(bst, tmp->val);// 用 tmp 覆盖 curcur->val = tmpVal;}
}除了迭代方法外,我们还可以使用递归方法来删除节点,下面的力扣题给出的方法就是递归方法。450. 删除二叉搜索树中的节点 - 力扣(LeetCode)
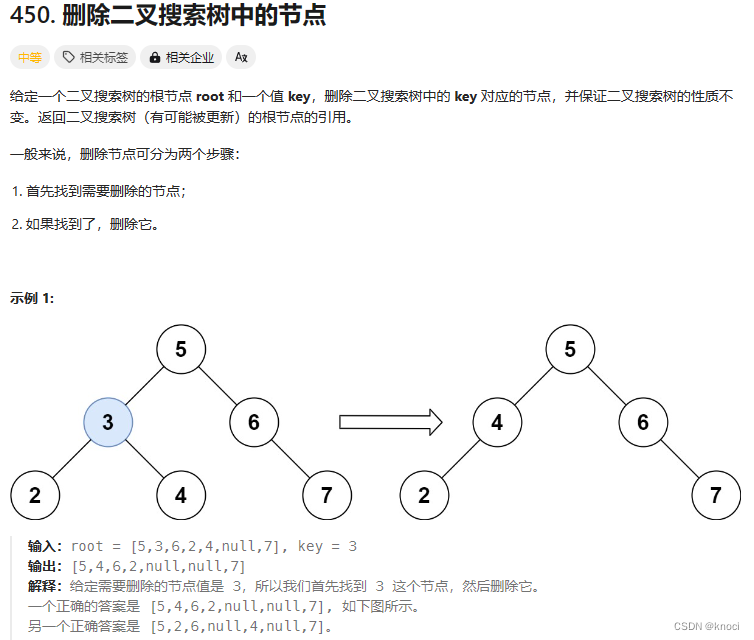
// 从二叉搜索树 root 中删除值为 key 的节点
struct TreeNode* deleteNode(struct TreeNode* root, int key) {// 如果根节点为空,直接返回 NULLif (root == NULL) {return NULL;}// 如果 key 小于当前节点值,递归删除左子树中的节点if (root->val > key) {root->left = deleteNode(root->left, key);return root;}// 如果 key 大于当前节点值,递归删除右子树中的节点if (root->val < key) {root->right = deleteNode(root->right, key);return root;}// 如果当前节点值等于 keyif (root->val == key) {// 如果当前节点没有左右子节点,直接返回 NULLif (!root->left && !root->right) {return NULL;}// 如果只有右子节点,返回右子节点if (!root->right) {return root->left;}// 如果只有左子节点,返回左子节点if (!root->left) {return root->right;}// 如果既有左子节点又有右子节点// 找到右子树中最小的节点作为当前节点的替代节点struct TreeNode *successor = root->right;while (successor->left) {successor = successor->left;}// 递归删除右子树中的最小节点root->right = deleteNode(root->right, successor->val);// 将替代节点的右子树连接到当前节点的右子树successor->right = root->right;// 将替代节点的左子树连接到当前节点的左子树successor->left = root->left;// 返回替代节点作为当前节点的父节点的子节点return successor;}// 返回根节点return root;
}
(4)中序遍历
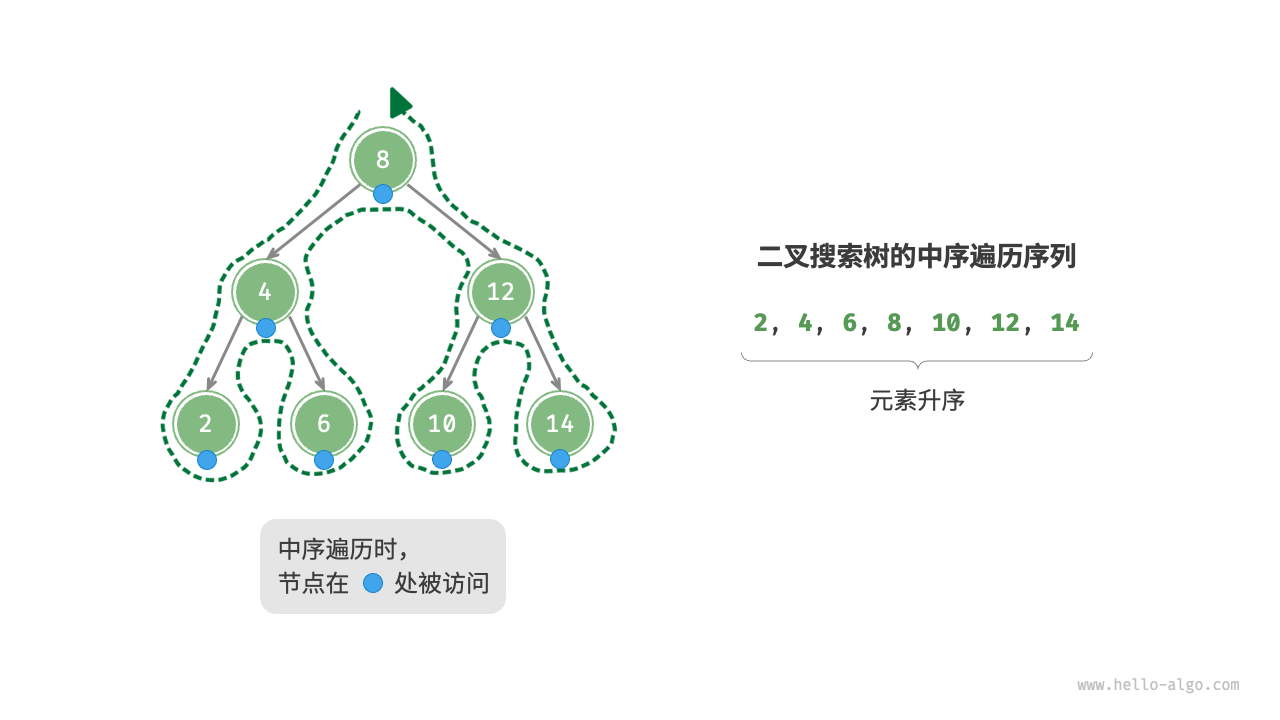
如图所示,二叉树的中序遍历遵循“左 → 根 → 右”的遍历顺序,而二叉搜索树满足“左子节点 < 根节点 < 右子节点”的大小关系。
这意味着在二叉搜索树中进行中序遍历时,总是会优先遍历下一个最小节点,从而得出一个重要性质:二叉搜索树的中序遍历序列是升序的。
利用中序遍历升序的性质,我们在二叉搜索树中获取有序数据仅需 𝑂(𝑛) 时间,无须进行额外的排序操作,非常高效。
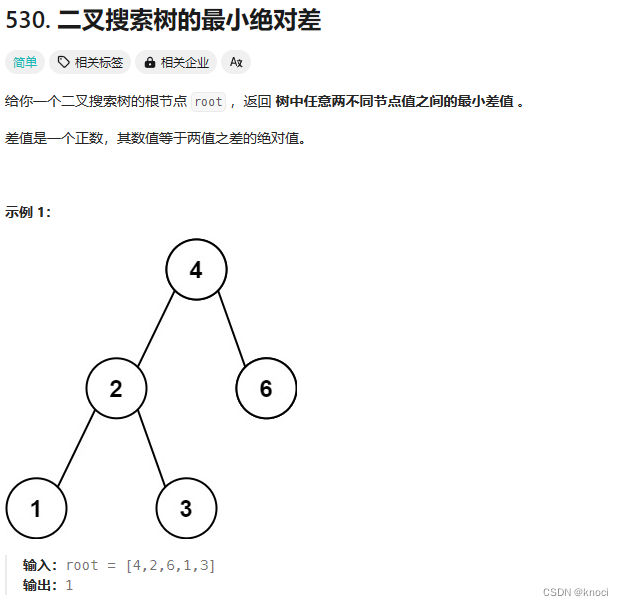
利用二叉搜索树中序遍历升序,我们可以完成 530. 二叉搜索树的最小绝对差
void traversal(struct TreeNode* cur, struct TreeNode** pre, int *result) {if (cur == NULL) return;//BST中序遍历是升序traversal(cur->left, pre, result); // 左if (*pre != NULL){ // 中*result = fmin(*result, cur->val - (*pre)->val);}*pre = cur; // 记录前一个traversal(cur->right, pre, result); // 右
}int getMinimumDifference(struct TreeNode* root) {int result = 114514;struct TreeNode* pre = NULL; // 初始值为NULLtraversal(root, &pre, &result); // 传递pre的指针的指针return result;
}







![[论文笔记]GAUSSIAN ERROR LINEAR UNITS (GELUS)](https://img-blog.csdnimg.cn/img_convert/28b6e6ca0e2cbdf1bdbbd7cb2fd3e3f5.png)