双目深度估计原理&立体视觉
- 0. 写在前面
- 1. 双目估计的大致步骤
- 2. 理想双目系统的深度估计公式推导
- 3. 双目标定公式推导
- 4. 极线校正理论推导
0. 写在前面
双目深度估计是通过两个相机的对同一个点的视差来得到给该点的深度。
标准系统的双目深度估计的公式推导需要满足:1)两个相机的光轴水平; 2) 两个相机焦距分辨率一致,也即内参一致;3)两个相机的成像平面水平,两个相机坐标系之间只存在x轴方向的平移关系。
但是得到的双目系统,不一定满足上述的三个条件,两个相机的坐标系之间大概率存在某个旋转平移关系,因此在使用标准系统的双目估计原理公式之前,需要首先完双目相机之间的外参标定,得到两者的旋转平移关系。
1. 双目估计的大致步骤
- 摄像头校准: 首先需要对双目摄像头进行校准,确保两个摄像头的成像参数(如焦距、主点位置、畸变参数等)已经准确标定。
- 立体视觉匹配: 使用立体视觉技术对左右两个摄像头捕获的图像进行匹配。这通常涉及在两个图像中找到对应的特征点或特征区域,比如角点、边缘等。
- 视差计算: 通过匹配得到的对应点,计算它们在左右图像之间的视差(disparity)。视差是指同一物体在两个图像中对应点的像素偏移量,视差越大表示物体距离摄像头越近。
- 三角测距: 利用视差信息和摄像头之间的几何关系,可以使用三角测量原理计算物体的距离。这通常需要知道摄像头的基线长度(两个摄像头之间的距离)和相机的内参(如焦距、主点位置等)。
- 深度估计: 根据视差信息和摄像头参数,可以进行深度估计,得到物体到摄像头的距离信息。这通常是通过将视差转换为实际距离的公式来实现的。
如果两个相机因为安装位置或者某些原因造成了不满足理想双目系统的萨格条件,就需要一些复杂的方法,最简单的方法就是得到两者的旋转平移矩阵,完成其中一个相机的旋转和平移,构造一个虚拟的相机(安装位置姿态与另一个相机之间满足理想双目系统)。
2. 理想双目系统的深度估计公式推导
双目深度估计是通 过两个相机的对同一个点的视差来得到给该点的深度。只要得到某个点在两个图片中的视差,就可以得出该点的深度。
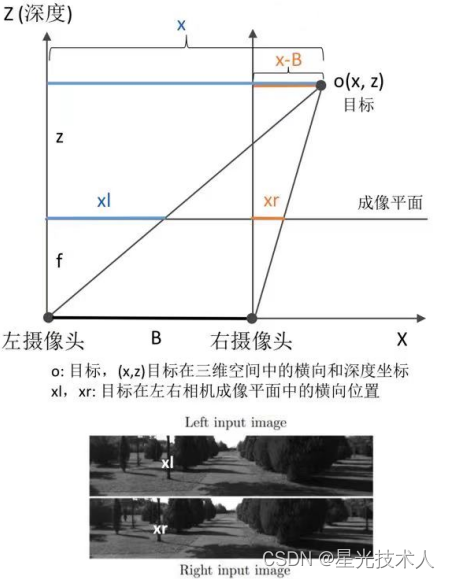
如图所示, B B B为基线长度, f f f为相机焦距, d d d为视差, x l , x r x_l,x_r xl,xr分别表示目标点在左右相机图像中的的像素u坐标。其中 f , B f,B f,B是固定值,深度计算步骤如下:
{ f z = x l x f z = x r x − B \begin{align} \begin{cases} {f \over z} = {x_l \over x } \\ {f \over z} = {x_r \over x-B} \end{cases} \end{align} {zf=xxlzf=x−Bxr
得,
z = f B x l − x r = f B d \begin{align} z = {fB \over x_l - x_r} = {fB \over d} \end{align} z=xl−xrfB=dfB
因此只要知道目标点在两个图片中得像素差,就能得到深度z。
3. 双目标定公式推导
因为得到得双目系统不一定为理想状态,所以需要得到两者得位姿关系。
事先声明如下定义:
p w p_w pw: 某目标点P在世界系下的笛卡尔3D坐标
p c l p_{cl} pcl:该点在左相机坐标系中的笛卡尔3D坐标
p c r p_{cr} pcr: 该点在右相机坐标系中的笛卡尔3D坐标
R c l w R_{cl}^w Rclw: 旋转关系convert a point from left camera coordinate to world
R c r w R_{cr}^w Rcrw: 旋转关系convert a point from right camera coordinate to world
t c l w t_{cl}^w tclw: 平移关系convert a point from left camera coordinate to world
t c r w t_{cr}^w tcrw: 平移关系convert a point from right camera coordinate to world
可以得到如下的关系
{ p w = R c l w ⋅ p c l + t c l w p w = R c r w ⋅ p c r + t c r w \begin{align} \begin{cases} p_w = R_{cl}^w \cdot p_{cl} + t_{cl}^w \\ p_w = R_{cr}^w \cdot p_{cr} + t_{cr}^w \end{cases} \end{align} {pw=Rclw⋅pcl+tclwpw=Rcrw⋅pcr+tcrw
式(3)可得
R c l w ⋅ p c l + t c l w = R c r w ⋅ p c r + t c r w \begin{align} R_{cl}^w \cdot p_{cl} + t_{cl}^w = R_{cr}^w \cdot p_{cr} + t_{cr}^w \\ \end{align} Rclw⋅pcl+tclw=Rcrw⋅pcr+tcrw
同乘 R c r w − 1 {R_{cr}^w}^{-1} Rcrw−1 得,
R c r w − 1 ⋅ R c l w ⋅ p c l + R c r w − 1 ⋅ t c l w = R c r w − 1 ⋅ R c r w ⋅ p c r + R c r w − 1 ⋅ t c r w R c r w − 1 ⋅ R c l w ⋅ p c l + R c r w − 1 ⋅ t c l w = p c r + R c r w − 1 ⋅ t c r w p c r = R c r w − 1 ⋅ R c l w ⋅ p c l + R c r w − 1 ⋅ t c l w − R c r w − 1 ⋅ t c r w \begin{align} {R_{cr}^w}^{-1} \cdot R_{cl}^w \cdot p_{cl} + {R_{cr}^w}^{-1} \cdot t_{cl}^w &={R_{cr}^w}^{-1} \cdot R_{cr}^w \cdot p_{cr}+ {R_{cr}^w}^{-1} \cdot t_{cr}^w \\ {R_{cr}^w}^{-1} \cdot R_{cl}^w \cdot p_{cl} + {R_{cr}^w}^{-1} \cdot t_{cl}^w &= p_{cr}+ {R_{cr}^w}^{-1} \cdot t_{cr}^w \\ p_{cr} &= {R_{cr}^w}^{-1} \cdot R_{cl}^w \cdot p_{cl} + {R_{cr}^w}^{-1} \cdot t_{cl}^w - {R_{cr}^w}^{-1} \cdot t_{cr}^w \end{align} Rcrw−1⋅Rclw⋅pcl+Rcrw−1⋅tclwRcrw−1⋅Rclw⋅pcl+Rcrw−1⋅tclwpcr=Rcrw−1⋅Rcrw⋅pcr+Rcrw−1⋅tcrw=pcr+Rcrw−1⋅tcrw=Rcrw−1⋅Rclw⋅pcl+Rcrw−1⋅tclw−Rcrw−1⋅tcrw
最终得,
p c r = R c l c r ⋅ p c l + t c l c r \begin{align} p_{cr} &= R_{cl}^{cr} \cdot p_{cl} + t_{cl}^{cr} \\ \end{align} pcr=Rclcr⋅pcl+tclcr
其中,
R c l c r = R c r w − 1 ⋅ R c l w t c l c r = R c r w − 1 ⋅ t c l w − R c r w − 1 ⋅ t c r w \begin{align} R_{cl}^{cr} &= {R_{cr}^w}^{-1} \cdot R_{cl}^w \\ t_{cl}^{cr} &= {R_{cr}^w}^{-1} \cdot t_{cl}^w - {R_{cr}^w}^{-1} \cdot t_{cr}^w \end{align} Rclcrtclcr=Rcrw−1⋅Rclw=Rcrw−1⋅tclw−Rcrw−1⋅tcrw
注意,式(9)(10)中左右相机世界系的位姿在完成左右相机各自的标定以后,就已经得到了。所以可以直接使用。一对棋盘格位姿的左右相机照片,就可以构成式(9)(10)两个。因为拍摄了多张图片,利用最小二乘法等某种非线性优化的的方式,最小化误差,即可得到我们最佳估计的 矩阵,有了这两个矩阵,就可以进一步进行两个相机的极线修正了。式(9)为右相机成像平面到左相机成像平面的旋转矩阵(convert a point from left camera coordinate to right camera).
4. 极线校正理论推导
通过3得到的两者的位姿关系,完成两个相机的极线矫正。进而通过2的步骤完成深度估计
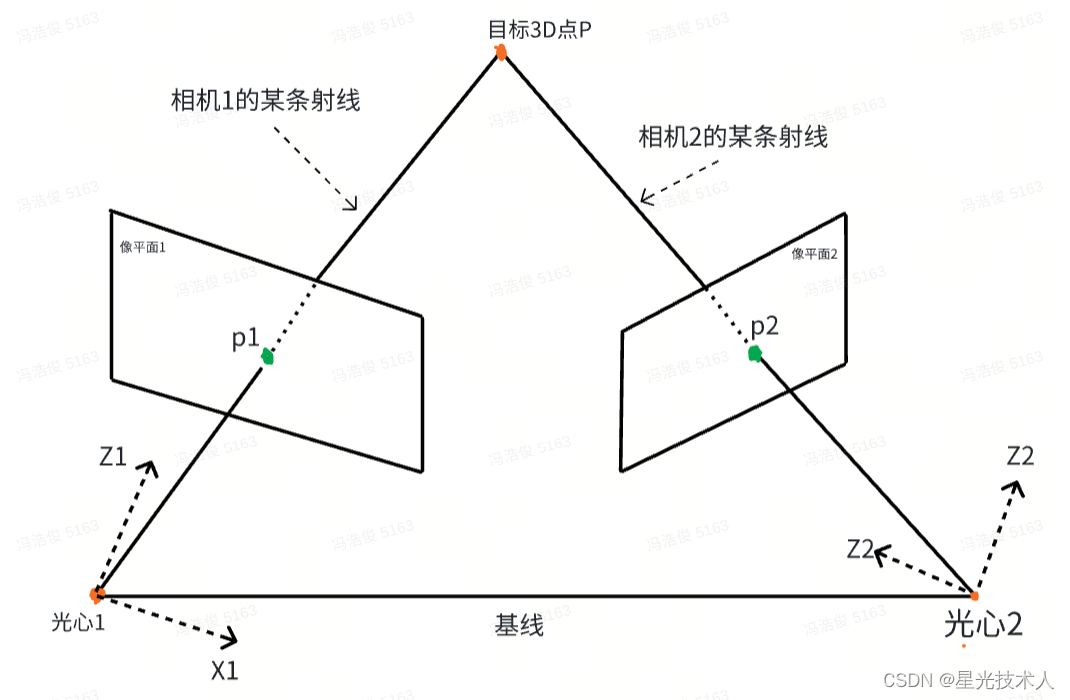
极线较正完成的是两个相机位置姿态的调整,使得左右相机达到理想双目系统的位置关系。下面是较正前后的位置状态对比‘极线校正的基本方法是对两幅图像做投影变换,使两幅图像上的对应匹配点所在的极线共线。本质上就是将相机固有的透视矩阵经过相应的几何变换得到新的透视矩阵,使得转换后的两幅图像的极线保持水平。最常见的校正方法就是Bouguet极线校正方法。opencv中的API名称为 cvStereoRectify
- 校正前的双目相机位姿关系
- 校正后的双目相机位姿关系
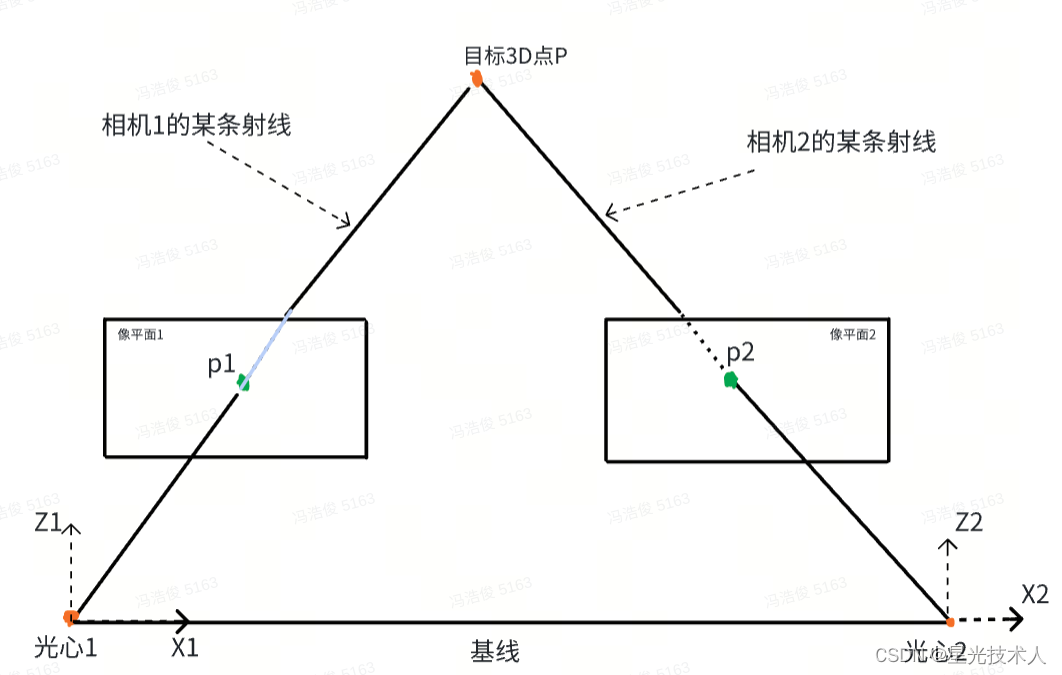
计算某个特征点的视差是在校正后的双目相机像平面中求得,需要注意的是,校正后的相机位置姿态是一个虚拟位置姿态,与原来的位置之间存在一个旋转关系(假如较正前后的光心位置一致),这个旋转关系就是单应矩阵,也是IPM算法思想的基础。
Bouguet极线校正方法:左右相机成像平面各旋转一半,使得左右图像重投影造成的误差最小,左右视图的共同面积最大。
使用 Bouguet 算法进行其极线校正的基本原理为:首先要最大限度得降低两幅双目图像中各帧的相同投影频次,其次要使每一帧的相同投射误差最小,最后尽量增加其观测的面积。设右相机成像平面到左相机成像平面的旋转矩阵为 cR ,然后把它分解为两个子旋转矩阵 1r 和 2r 。当使用这两个左右转换矩阵分别旋转左右相机时,两相机刚好能产生 1/2 角点上的旋转量,因此主光线向量的朝向能和旋转前维持一致。
后边的过程等以后需要的时候再做研究



https://zhuanlan.zhihu.com/p/362018123
chrome-extension://oemmndcbldboiebfnladdacbdfmadadm/https://engineering.purdue.edu/~byao/Thesis/%E7%A1%95%E5%A3%AB%E8%AE%BA%E6%96%87-%E9%9F%A9%E4%BF%A1_ZJU16.pdf
https://blog.csdn.net/x_r_su/article/details/52683754