上篇博客，学习了栈，我们可以知道他也是一种线性表，遵从先进后出的原则，在本节，我们进一步学习另一种线性表—队列。就像饭堂里排队打饭的的队伍，作为一种先进先出的线性表，他又有哪些特别之处呢？又该如何应用呢？接下来，跟我走近队列的世界里。

目录

一、队列的应用场景

二、队列的基本概念和结构

2.1 队列的基本概念

2.2 队列的结构

2.3 队列的实现方式

三、循环队列栈的接口函数实现

3.0  循环队列设计的思想来源

3.0.1 从数组存放的角度分析

3.0.2 从时间复杂度的角度分析

3.1 循环队列的三个关键问题及如何解决？

3.2  循环队列的特点

3.3  循环队列的接口函数 

3.4  循环队列的设计（结构体）

3.5  循环队列的初始化

3.6 入队

3.7 出队

3.8 获取队头元素值

3.9 获取有效元素个数

3.10 判空

3.11 判满

3.12 扩容（无法直接扩容！循环队列的最致命缺陷）

3.13 打印

3.14 清空

3.15 销毁

四、总结

---

一、队列的应用场景

       队列是一种常见的数据结构，具有先进先出（FIFO）的特性，适用于许多场景，包括但不限于以下几个方面：

1. 任务调度： 队列可用于任务调度系统，例如处理异步任务或者在系统中处理任务队列。任务可以按照提交的顺序排队执行，确保公平性和顺序性。

2. 消息队列：消息队列是分布式系统中常见的通信模式，用于在不同组件或服务之间传递消息。生产者将消息推送到队列的尾部，而消费者则从队列的头部获取消息。这种模式在微服务架构中广泛应用，用于解耦各个服务之间的通信。

3. 缓冲区：队列常被用作缓冲区，用于在生产者和消费者之间进行数据传输。例如，计算机网络中的数据包可以在路由器或交换机上排队等待处理。

4. 广度优先搜索（BFS）：在图论和树结构中，BFS算法常用队列来实现。它从起始顶点开始，先遍历其所有相邻的节点，然后逐层遍历其他节点，确保以最短路径访问所有节点。

5. 资源分配：队列可用于管理资源的分配，例如操作系统中的进程调度，或者服务器中的请求队列管理，确保资源按照特定规则分配给请求者。

6. 多线程编程：在多线程编程中，队列常被用作线程安全的数据结构，用于线程之间的通信和同步。一个线程可以将数据放入队列，而另一个线程则可以从队列中取出数据进行处理。

二、队列的基本概念和结构

2.1 队列的基本概念

      队列是一种先进先出（first in first out,FIFO）的线性表，是一种常用的数据结构。

它只允许在表的一端（front）进行删除操作，而在表的另一端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。（队尾入队头出）队列中没有元素时，称为空队列。

2.2 队列的结构

  队尾中的元素遵从先进先出的原则，特别像是排队购票的过程。它的结构如下：

2.3 队列的实现方式

    队列的实现方式和栈类似，按照存储结构划分：基于顺序存储结构（数组存放）的循环队列、基于链式存储结构的链式队列。本节主要学习循环队列！

三、循环队列栈的接口函数实现

3.0  循环队列设计的思想来源

3.0.1 从数组存放的角度分析

       队列的顺序存储结构和顺序栈类似，在队列的顺序存储结构中，除了用一组地址连续的存储单元依次存放从队列头到队列尾的元素之外，还需要设置头尾两个指针front和rear，分别指示队列头元素及队尾元素的位置。（数组元素不动，让数组的下标变化）

我们规定：

• 初始化建立空队列时，令front=rear=0
• 每当插入新的队尾元素时，“尾指针增1”
• 每当删除队头元素时，“头指针增1”
• 在非空队列中，头指针始终指向队列头元素，尾指针始终指向队列尾元素的下一个位置

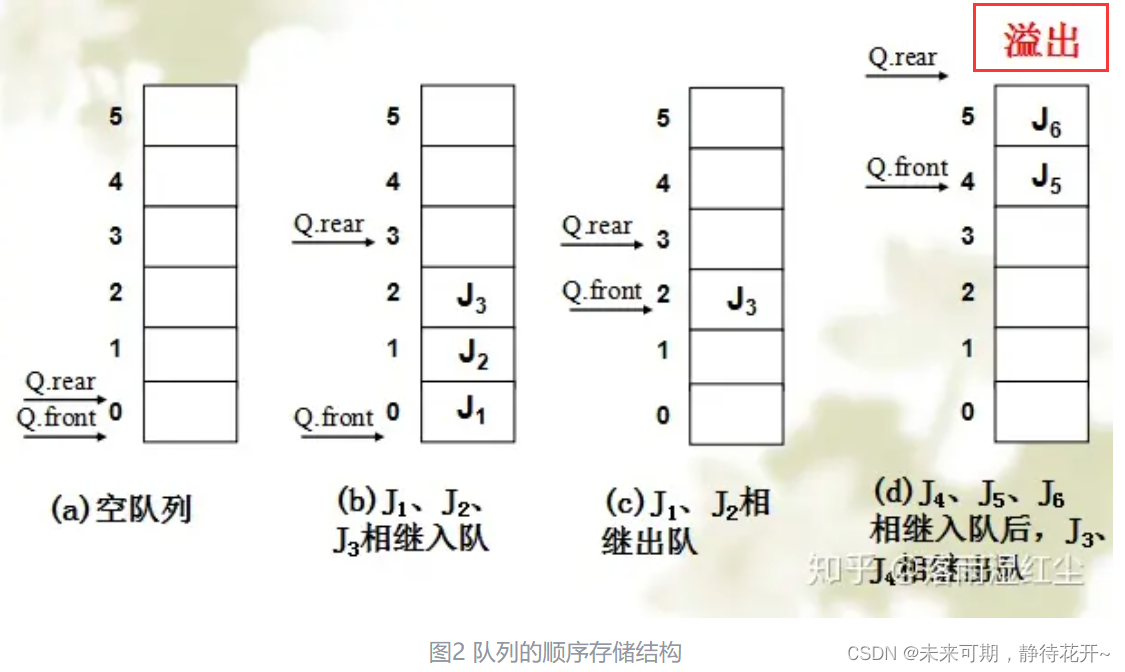
存在的问题：在入队和出队的操作中，头尾指针只增加不减小，致使被删除元素的空间永远无法重新利用，因此，尽管队列中实际的元素个数远远小于向量空间的规模，但也可能由于尾指针巳超出向量空间的上界而不能做入队操作，该现象称为假溢出！

         当进行动态创建队列的时候，也只不过是向后继续不断的申请内存空间，即时前面出队操作释放掉了前面的空间，但是指针依旧会向后进行移动，直到达到系统预留给程序的内存上界被强行终止，这对于极为频繁的队列操作和程序而言是致命的，这时候，就需要对我们的队列进行优化，使用更为优秀的结构——循环队列。

解决办法：将顺序队列臆造为一个环状的空间，称之为循环队列

3.0.2 从时间复杂度的角度分析

         在设计顺序栈时，入栈和出栈的操作，数据都是通过尾插或者尾删进行的，很明显它的入栈和出栈时间复杂度都是O(1)，在设计链式栈时，入栈和出栈的操作，数据都是通过单链表的头插和头删进行的，很明显它的入栈和出栈的时间复杂度也都是O(1)，那么我们如何设计顺序队列，让队列也能达到O(1)的时间复杂度呢？即如何确定队头和队尾的位置？是放在数组的头部还是尾部？

      从上面的分析可知，如果只是简单的用一个动态数组存放队的数据，不管队头和队尾设计在哪一个位置，它的入队和出队的时间复杂度不可能同时达到O(1)，因此，我们应该如何解决呢？    ——>既然数据动达不到时间复杂度的要求，那我们便换个思路，让数据不动，让数组元素的下标动，设置队头队尾两个指针front和rear，分别指示队列头元素及队尾元素的位置。这样每次插入和删除便不需要挪动数据，达到O(1)的时间复杂度要求。这便引入了循环队列的概念

3.1 循环队列的三个关键问题及如何解决？

①:如何让入队，出队时间复杂度都达到O(1)？

我们规定：

• 初始化建立空队列时，令front=rear=0
• 每当插入新的队尾元素时，“尾指针增1”
• 每当删除队头元素时，“头指针增1”
• 在非空队列中，头指针始终指向队列头元素，尾指针始终指向队列尾元素的下一个位置

②:怎么判满，怎么判空?

 

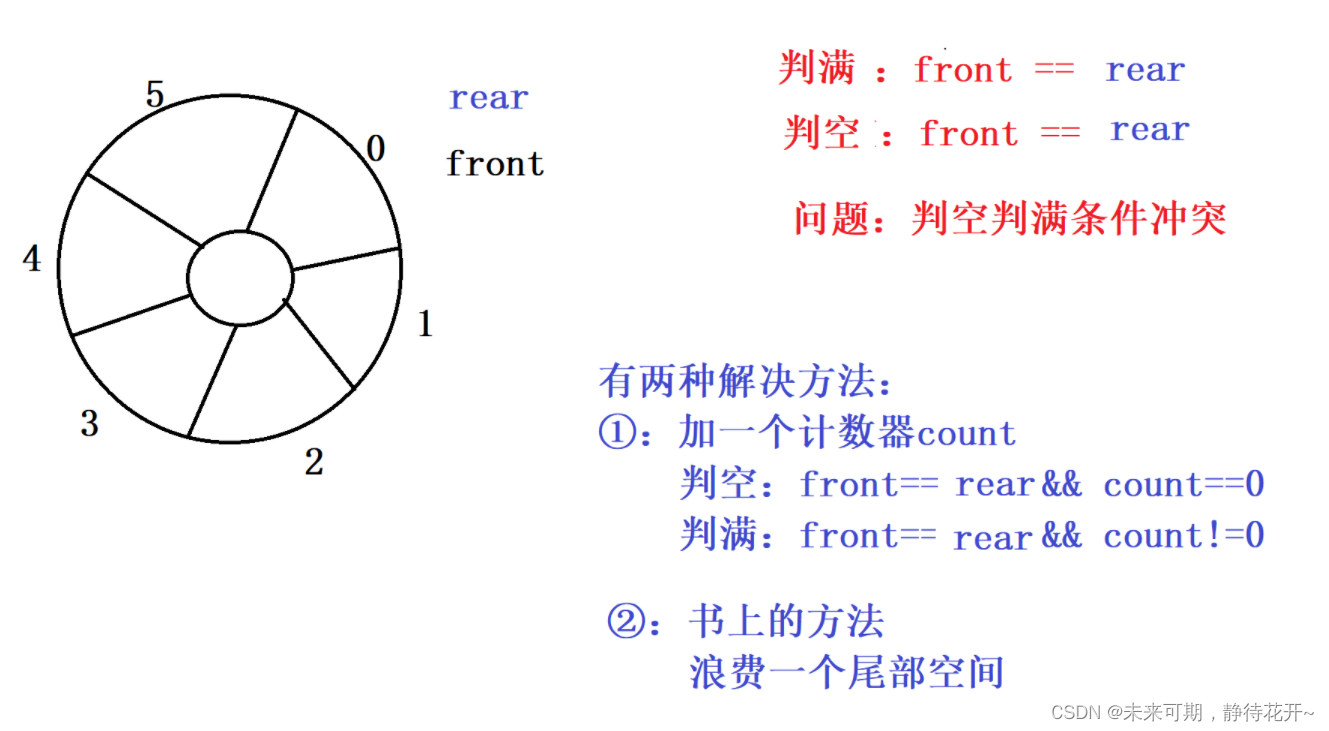
     从上面分析我们可以看到：判空与判满的条件一样，那到底是数组存满，还是数组是空数组，该如何区分呢？ 主要采用第二种方法：浪费掉最后一个数组空间，以此对二者进行区分！如下所示：

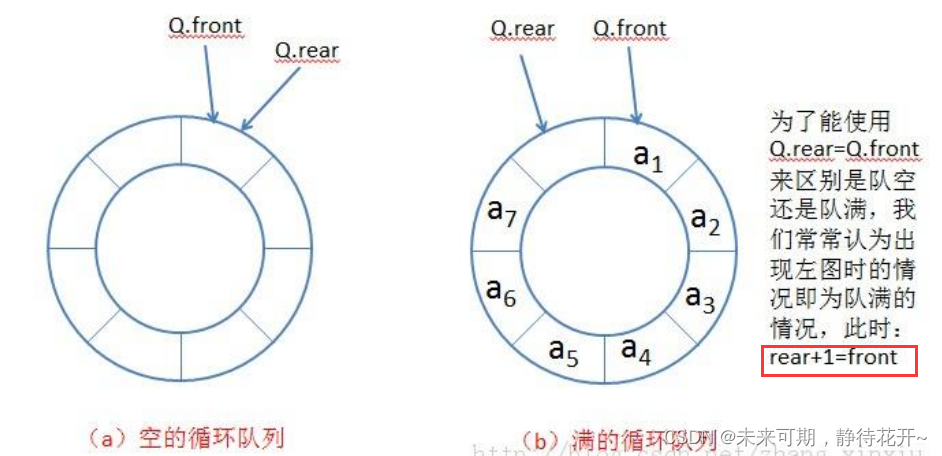
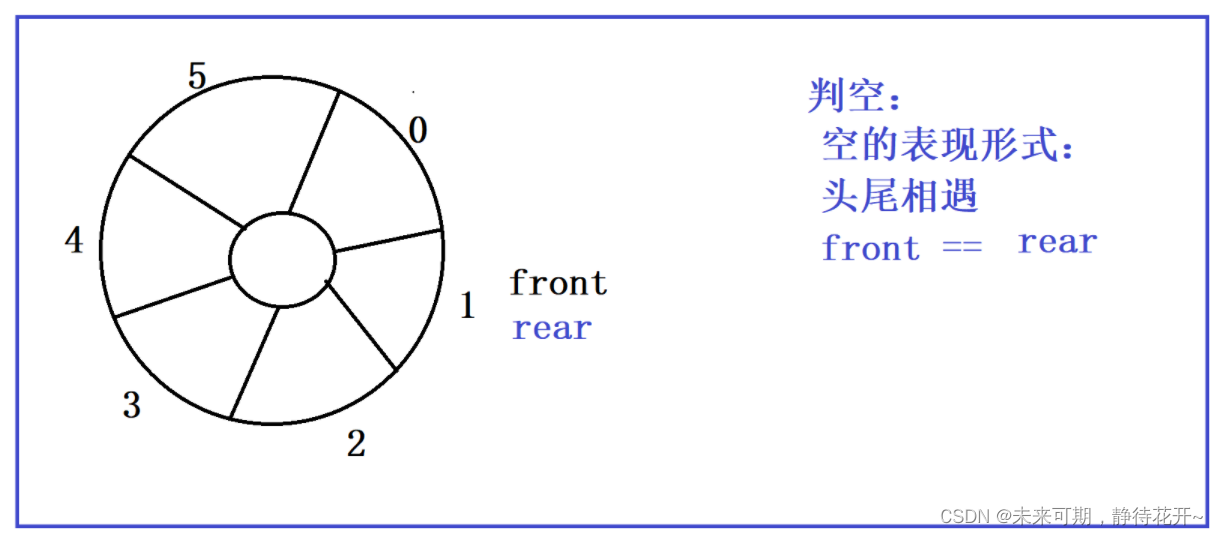
        在队满时，队尾小于队头，条件rear+1=front是可以用来判断的，但是当队尾大于队头（越过最大下标和0下标），此时这个条件就不能在使用了，如下图所示队列已经满了：rear+1为6，而此时front等于0，二者不相等，这个条件不能作为判满的条件，那么又该如何修正呢？区域操作！ 这样让队尾的值一值在0-maxsize之间，此时便不会越界，可以正常使用！

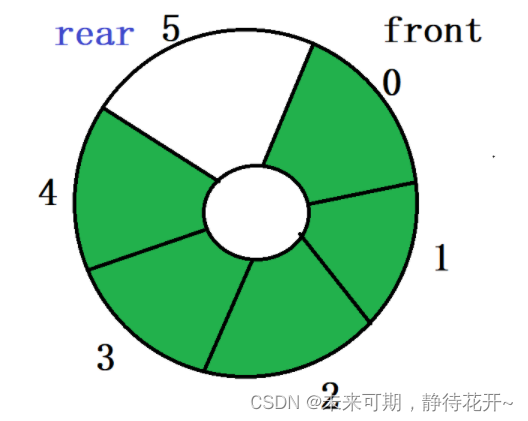
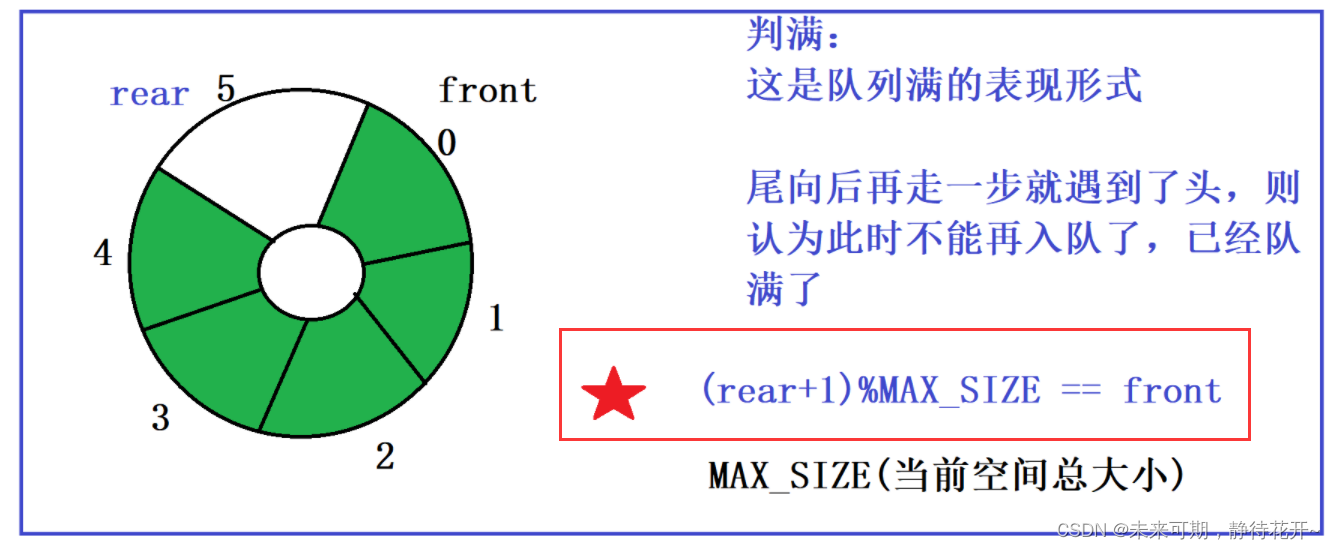
③怎么获取有效元素个数?

 

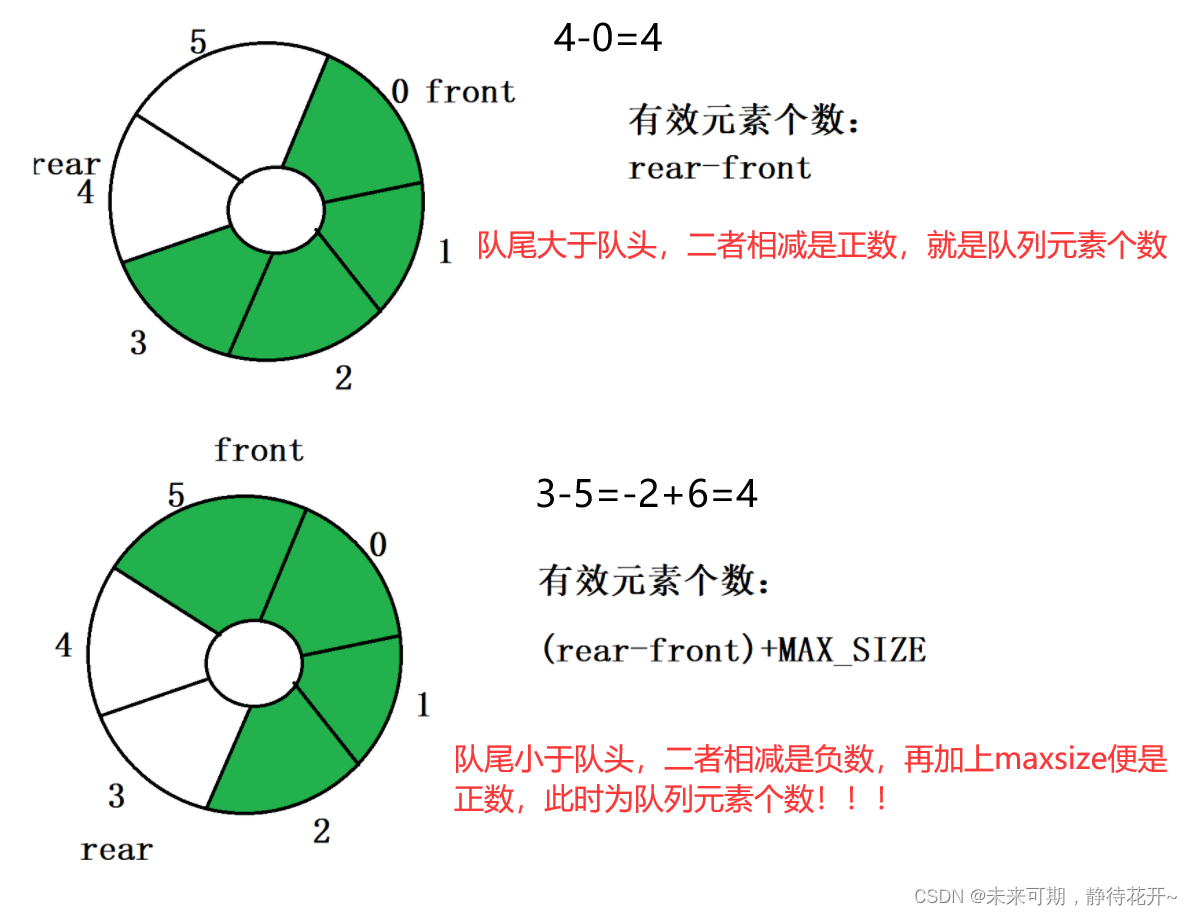
通过上面分析，求元素个数有两个公式，那么有没有办法可以统一上面两个公式？当然是有的。 

 总结：

3.2  循环队列的特点

循环队列的特点主要体现在以下几个方面：

1. 大小固定：循环队列的大小是固定的，一旦定义就不能改变。当存储空间的最后一个位置已被使用，而再要进行入队运算时，只需要存储空间的第一个位置空闲，就可以将元素加入到第一个位置，即将存储空间的第一个位置作为队尾。
2. 无溢出风险：循环队列通过队头和队尾两个指针来描述队列中的数据存储位置，可以有效地防止“假溢出”现象的发生。在实际应用中，当存储空间全满或者空时，都有front=rear的情况。通过这种方式，循环队列可以更简单、高效地解决顺序队列的“假溢出”问题。
3. 高效的插入和删除操作：循环队列支持在队尾一端进行插入操作，而在队头一端进行删除操作。这一特性使得循环队列的插入和删除操作非常高效。
4. 空间利用率高：循环队列通过队头和队尾两个指针连成一个环状的空间，充分利用了数组的空间。当存储空间的最后一个位置已被使用，而再要进行入队运算时，只需要存储空间的第一个位置空闲，就可以将元素加入到第一个位置，这样就可以减少内存的浪费，提高空间利用率。
5. 应用场景广泛：由于其高效的插入和删除操作、空间利用率高以及能够动态调整队列大小的特性，循环队列在许多领域都有广泛的应用，如操作系统中的任务调度、通信协议中的数据包处理、线程池中的线程管理等。
6. 循环队列的一个致命的缺陷就是：无法直接进行扩容！！！必须重新开辟内存空间！

3.3  循环队列的接口函数 

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include "queue.h"//初始化
void Init_Queue(struct Queue* que);//入队
void Push(struct Queue* que, ELEM_TYPE val);//出队
void Pop(struct Queue* que);//获取队头元素值
ELEM_TYPE Front(struct Queue* que);//获取有效元素个数
int Get_length(struct Queue* que);//判空
bool IsEmpty(struct Queue* que);//判满
bool IsFull(struct Queue* que);//清空
void Clear(struct Queue* que);//销毁
void Destroy(struct Queue* que);//打印
void Show(struct Queue* que);

3.4  循环队列的设计（结构体）

     本质和顺序栈的设计差不多，只不过这里主要为3个成员，申请空间的指针（相当于顺序表中用来申请内存空间的指针）、队头指针（用来标记对头的位置），队尾指针（用来标记对尾的位置），简单起见，用整型变量front、rear即可，只不过循环队列无法直接扩容，因此不需要记录队列容量的变量capacity!

//循环队列的结构体设计
#define MAX_SIZE 10
typedef int ELEM_TYPE;typedef struct Queue
{ELEM_TYPE *base;int front;   //队头指针int rear;    //队尾指针
}Queue, *PQueue;

3.5  循环队列的初始化

      循环队列在创建以后必须要进行初始化，否则内部为随机值，无法使用。循环队列的初始化主要是对结构体成员赋初值。核心就在于申请空间以及将front指针和rear指针内容赋值为0，即指向第0个元素即可（注意第 0个元素内容为空）。

//初始化
void Init_Queue(struct Queue* que)
{第0步：参数检测assert(que!=NULL);第1步：初始化赋值que->base = (ELEM_TYPE *)malloc(MAX_SIZE * sizeof(ELEM_TYPE));que->front = que->rear =0;
}

3.6 入队

     入队操作方法，直接将rear向后移动即可，但是要注意判断，如果rear达到了队列的空间上线，将要从头继续开始移动，这里推荐使用余数法，即无论如何求余都是在这片空间内进行操作，防止一次错误执行就直接整体崩溃，而且也相对而言更为简洁，不推荐使用if语句，这样显得比较累赘。注意进行加一移动位置操作的时候，不能直接q->rear++这样的操作，这样计算机判断优先级会产生让自己意想不到的后果，此外这里还需要进行一次是否队列已满的判断，当我们rear指针的下一个位置就是front的位置的时候，即改循环队列已满。

//入队
void Push(struct Queue* que, ELEM_TYPE val)
{第0步：参数检测assert(que!=NULL);//1.判满if(IsFull(que)){return;}//2.给rear指向的下标赋值，进行入队操作que->base[que->rear] = val;//3.rear++(这里需要注意越界)que->rear = (que->rear+1)%MAX_SIZE;}

3.7 出队

     循环队列的出队操作，直接将front进行后移一位即可，注意这时候有一个需要留意的地方，即队列是否为空，当队列为空的时候是无法进行出队操作的。

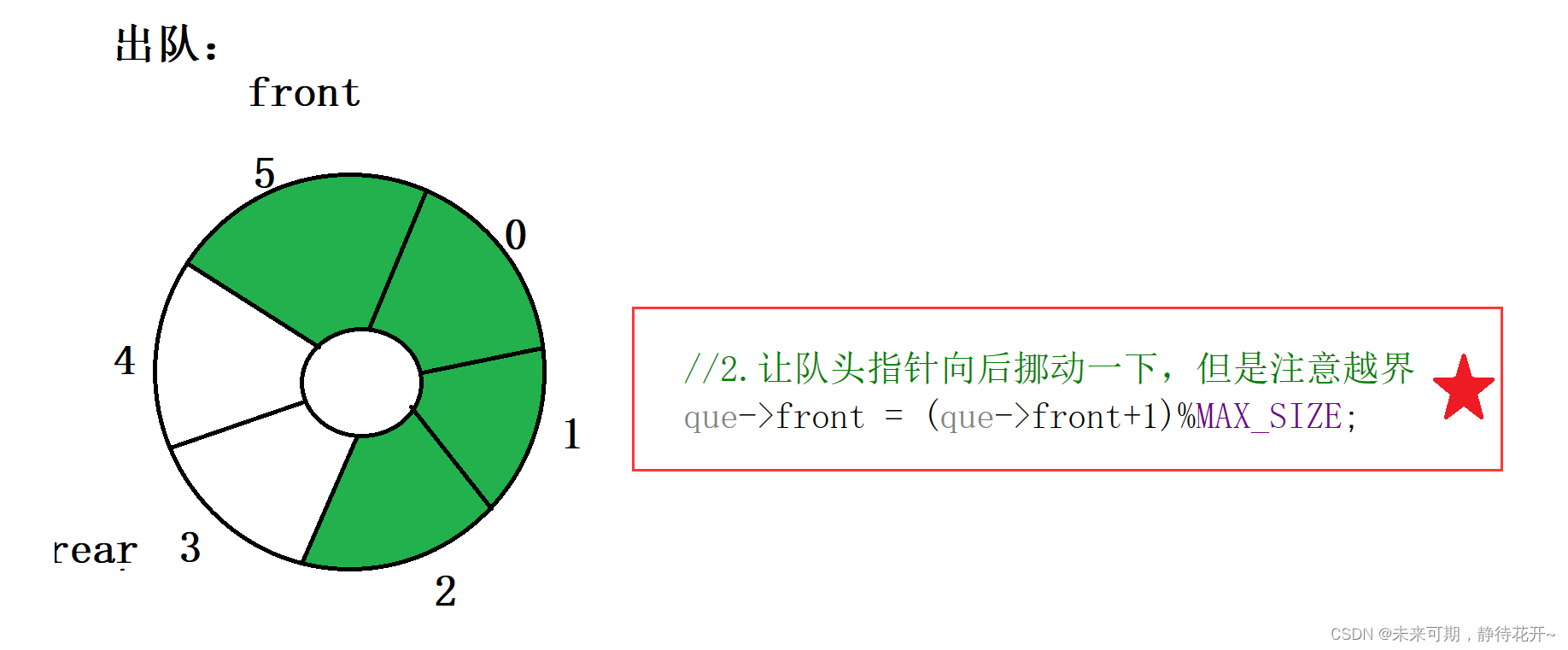
//出队
void Pop(struct Queue* que)
{第0步：参数检测assert(que!=NULL);//1.判空if(IsEmpty(que)){return;}//2.让队头指针向后挪动一下，但是注意越界que->front = (que->front+1)%MAX_SIZE;}

3.8 获取队头元素值

直接返回front下标对应的数组元素即可！

//获取队头元素值
ELEM_TYPE Front(struct Queue* que)
{ 第0步：参数检测assert(que!=NULL);return que->base[que->front];
}

3.9 获取有效元素个数

直接利用公式计算，返回即可

//获取有效元素个数
int Get_length(struct Queue* que)
{第0步：参数检测assert(que!=NULL);return ((que->rear-que->front)+MAX_SIZE)%MAX_SIZE;
}

3.10 判空

直接用队列判空的条件即可！

//判空
bool IsEmpty(struct Queue* que)
{第0步：参数检测assert(que!=NULL);return que->front == que->rear;
}

3.11 判满

直接用队列判满的条件即可！

//判满
bool IsFull(struct Queue* que)
{第0步：参数检测assert(que!=NULL);return (que->rear + 1)%MAX_SIZE == que->front;
}

3.12 扩容（无法直接扩容！循环队列的最致命缺陷）

       循环队列之所以无法在原地进行扩容，主要是因为在循环队列中，队列的元素是顺序排列的，而且循环队列的底层通常是通过数组来实现的。在数组中，元素是连续存储的，当数组空间不足以容纳更多的元素时，需要进行扩容，即分配一个更大的数组来存储元素。

但是，在循环队列中，元素的排列是循环的，即队列头部和尾部可能相邻，而队列的元素在数组中是连续存储的。当队列需要扩容时，如果直接在原数组上扩容，可能会因为数组的连续性导致无法满足队列头部和尾部相邻的条件，从而破坏了循环队列的特性。

        因此，为了实现循环队列的扩容，通常需要创建一个新的更大的数组，并将原数组中的元素按照顺序复制到新数组中，同时保持循环队列的循环特性。这种方式虽然需要额外的空间和时间来进行复制操作，但可以保证扩容后的循环队列仍然是正确的。

3.13 打印

从队头到队尾遍历所有元素打印即可！

//打印
void Show(struct Queue* que)
{第0步：参数检测assert(que!=NULL);for(int i=que->front; i!=que->rear; i=(i+1)%MAX_SIZE){printf("%d ", que->base[i]);}printf("\n");}

3.14 清空

直接让队头指针和队尾指针相等即可！

//清空
void Clear(struct Queue* que)
{第0步：参数检测assert(que!=NULL);que->front = que->rear = 0;
}

3.15 销毁

直接让队头指针和队尾指针相等，然后再释放即可！

//销毁
void Destroy(struct Queue* que)
{第0步：参数检测assert(que!=NULL);que->front = que->rear = 0;free(que->base);que->base = NULL;
}

四、总结

       以上便是我为大家带来的循环队列设计内容，若有不足，望各位大佬在评论区指出，谢谢大家！下一节继续进行链式队列的内容，感兴趣的你可以留下你们的点赞、收藏和关注，这是对我极大的鼓励，我也会更加努力创作更优质的作品。再次感谢大家！