文章目录
数组和特殊矩阵
考纲内容
复习提示
前言
1.数组的定义
2.数组的存储结构
3.特殊矩阵的压缩存储
3.1对称矩阵
3.2三角矩阵
3.3三对角矩阵
4.稀疏矩阵
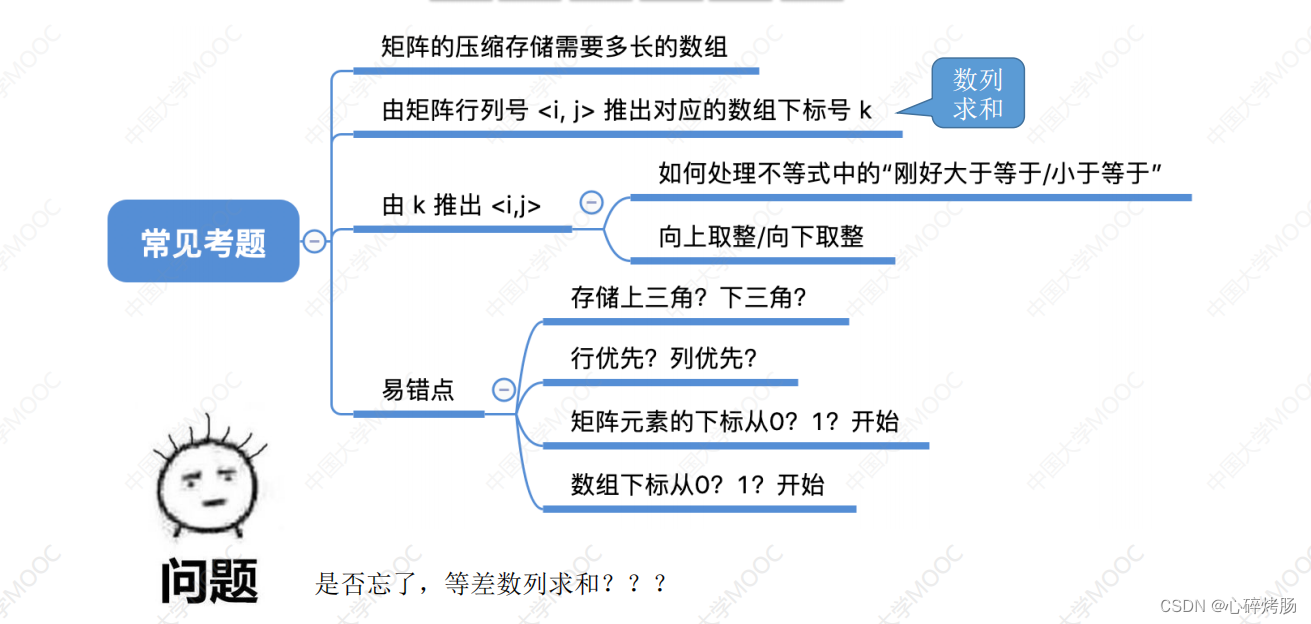
5.知识回顾
数组和特殊矩阵
考纲内容
(一)栈和队列的基本概念
(二)栈和队列的顺序存储结构
(三)栈和队列的链式存储结构
(四)多维数组的存储(五)特殊矩阵的压缩存储
(六)栈、队列和数组的应用
复习提示
本章通常以选择题的形式考查,题目不算难,但命题的形式比较灵活,其中栈(出入栈的过程、出栈序列的合法性)和队列的操作及其特征是重点。因为它们均是线性表的应用和推广,所以也容易出现在算法设计题中。此外,栈和队列的顺序存储、链式存储及其特点、双端队列的特点、栈和队列的常见应用,以及数组和特殊矩阵的压缩存储都是必须掌握的内容。
前言
矩阵在计算机图形学、工程计算中占有举足轻重的地位。在数据结构中考虑的是如何用最小的内存空间来存储同样的一组数据。所以,我们不研究矩阵及其运算等,而把精力放在如何将矩阵更有效地存储在内存中,并能方便地提取矩阵中的元素。
1.数组的定义
数组是由n(n>1)个相同类型的数据元素构成的有限序列,每个数据元素称为一个数组元素,每个元素在n个线性关系中的序号称为该元素的下标,下标的取值范围称为数组的维界。
数组与线性表的关系:数组是线性表的推广。一维数组可视为一个线性表;二维数组可视为其元素是定长数组的线性表,以此类推。数组一旦被定义,其维数和维界就不再改变。因此,除结构的初始化和销毁外,数组只会有存取元素和修改元素的操作。
2.数组的存储结构
大多数计算机语言都提供了数组数据类型,逻辑意义上的数组可采用计算机语言中的数组数据类型进行存储,一个数组的所有元素在内存中占用一段连续的存储空间。
以一维数组 A[0..n-1]为例,其存储结构关系式为:
其中,L是每个数组元素所占的存储单元。
二维数组按行优先存储的下标对应关系
对于多维数组,有两种映射方法:按行优先和按列优先。
以二维数组为例,按行优先存储的基本思想是:先行后列,先存储行号较小的元素,行号相等先存储列号较小的元素。
设二维数组的行下标与列下标的范围分别为[0,h1]与[0,h2],则存储结构关系式为:
例如,对于数组 A[2][3],它按行优先方式在内存中的存储形式如图 3.18所示。

当以列优先方式存储时,得出存储结构关系式为:
例如,对于数组 A[2][3],它按列优先方式在内存中的存储形式如图 3.19所示。


3.特殊矩阵的压缩存储
压缩存储:指为多个值相同的元素只分配一个存储空间,对零元素不分配空间。
特殊矩阵:指具有许多相同矩阵元素或零元素,并且这些相同矩阵元素或零元素的分布有一定规律性的矩阵。
常见的特殊矩阵:对称矩阵、上(下)三角矩阵、对角矩阵等。
特殊矩阵的压缩存储方法:找出特殊矩阵中值相同的矩阵元素的分布规律,把那些呈现规律性分布的、值相同的多个矩阵元素压缩存储到一个存储空间中。
3.1对称矩阵
[命题追踪-对称矩阵压缩存储的下标对应关系]
若对一个 n阶矩阵 A 中的任意一个元素 a ᵢ,ⱼ都有 a ᵢ,ⱼ = a ⱼ,ᵢ (1<=i,j<=n),则称其为对称矩阵。
其中的元素可以划分为3个部分,即上三角区、主对角线和下三角区。

对于n阶对称矩阵,上三角区的所有元素和下三角区的对应元素相同,若仍采用二维数组存放,则会浪费几乎一半的空间,为此将n阶对称矩阵A存放在一维数组B[n(n+1)/2]中,即元素aᵢ,ⱼ,存放在bₖ以中。比如只存放下三角部分(含主对角)的元素。
在数组B中,位于元素aᵢ,ⱼ (i=>j)前面的元素个数为
第1行:1个元素(a₁,₁)。
第2行:2个元素(a₂,₁,a₂,₂)。
. . . . . .
第i-1行:i-1个元素(aᵢ-₁,₁, aᵢ-₁,₂,…,aᵢ-₁ ,ᵢ-₁ )。
第i行:j-1个元素(aᵢ,₁,aᵢ,₂,…,aᵢ,ⱼ-₁)。
因此,元素aᵢ,ⱼ 在数组B中的下标k=1+2+…+(i-1)+j-1=i(i-1)/2+j-1(数组下标从 0开始)。
因此,元素下标之间的对应关系如下:


注意:
二维数组 A[n] [n](行列都是n个元素)和 A[0..n-1] [0..n-1](行列都是n个元素)的写法是等价的。若数组写为 A[1..n][1..n],则说明指定了从下标 1开始存储元素。二维数组元素写为 a[i][j],注意数组元素下标i和j通常是从0开始的。矩阵元素通常写为 ai,j或 a(i)(j),注意行号i和列号j是从1开始的。
3.2三角矩阵
下三角矩阵[见图3.22(a)]中,上三角区的所有元素均为同一常量。其存储思想与对称矩阵类似,不同之处在于存储完下三角区和主对角线上的元素之后,紧接着存储对角线上方的常量一次,所以可以将n阶下三角矩阵A压缩存储在B[n(n+1)/2+1]中。
元素下标之间的对应关系为:

下三角矩阵在内存中的压缩存储形式如图3.21所示


[命题追踪-上三角矩阵采用行优先存储的应用]
上三角矩阵[见图 3.22(b)]中,下三角区的所有元素均为同一常量。只需存储主对角线、上三角区上的元素和下三角区的常量一次,可将其压缩存储在B[n(n+1)/2+1]中。
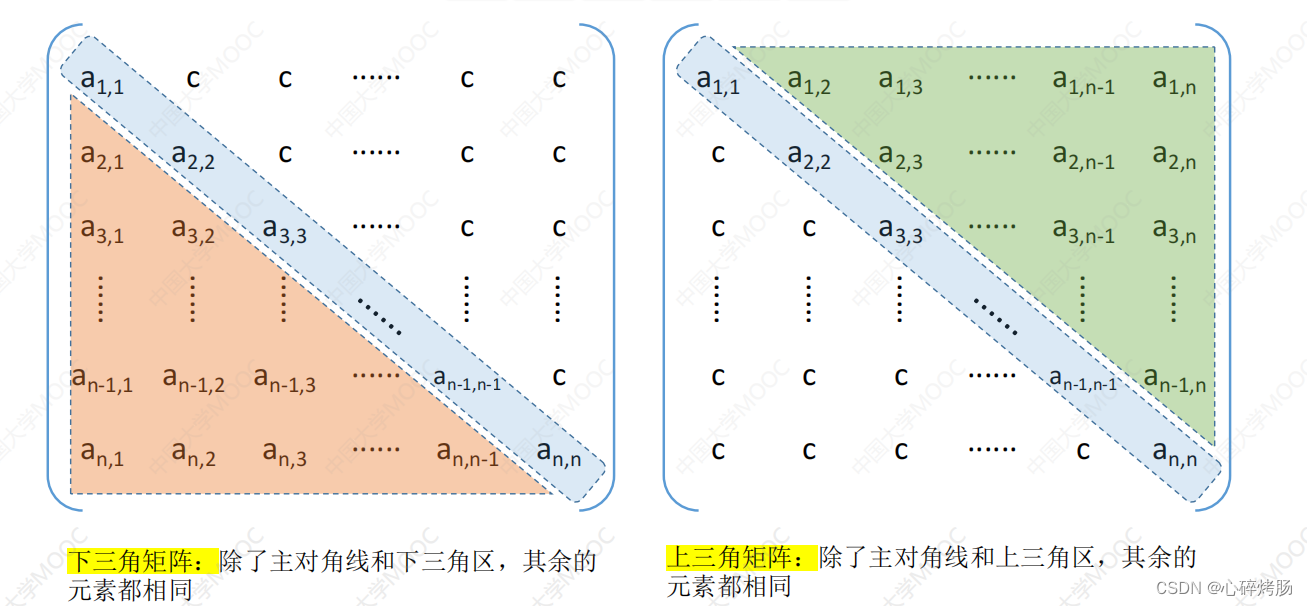
在数组B中,位于元素aᵢ,ⱼ (i<=j)前面的元素个数为:
第1行:n个元素
第2行:n-1个元素
. . . . . .
第i-1行:n-i+2个元素
第i行:j-i个元素
因此,元素 aᵢ,ⱼ 在数组B中的下标
k=n+( n-1 )+…+( n-i+2 )+( j-i+1 )-1=( i-1 )( 2n-i +2 )/2+( j-i )
因此,元素下标之间的对应关系如下:
上三角矩阵在内存中的压缩存储形式如图所示。

以上推导均假设数组的下标从0开始,若题设有具体要求,则应该灵活应对。

3.3三对角矩阵
对角矩阵也称带状矩阵。对n阶矩阵A中的任意一个元素a,,当 |i-j| >1时,若有aᵢ,ⱼ =0(1<=i,j<=n),则称为三对角矩阵。在三对角矩阵中,所有非零元素都集中在以主对角线为中心的3条对角线的区域,其他区域的元素都为零。
三对角矩阵A也可以采用压缩存储,将3条对角线上的元素按行优先方式存放在一维数组B中,且a存放于B[0]中,其存储形式如图3.25 所示。


[命题追踪-三对角矩阵压缩存储的下标对应关系]
由此可以计算矩阵A中3条对角线上的元素aᵢ,ⱼ(1≤i,j≤n,|i-j|≤1)在一维数组B中存放的下标为k=2i+j-3。
反之,若已知三对角矩阵中的某个元素aᵢ,ⱼ存放在一维数组B的第k个位置,则有i=[(k+ 1)/3+1],j=k-2i+3。
例如:
当k=0时,i=[(0+1)/3+1]=1,j=0-2x1+3=1,存放的是a₁,₁;
当k=2时,i=[(2+1)/3+1]=2,j=2-2x2+3=1,存放的是a₂,₁ ;
当k=4时,i=[(4+1)/3+1]=2,j=4-2x2+3=3,存放的是a₂,₃。
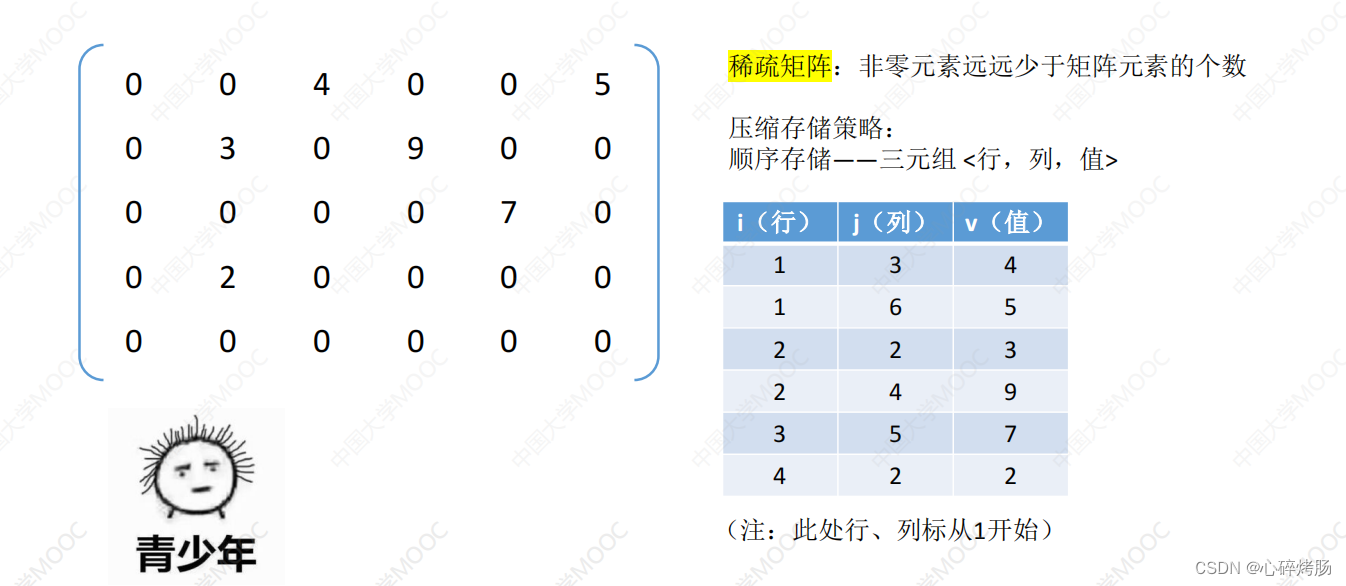
4.稀疏矩阵
矩阵中非零元素的个数t,相对矩阵元素的个数s来说非常少,即s>>t的矩阵称为稀疏矩阵。
例如,一个矩阵的阶为100x100,该矩阵中只有少于100个非零元素。
[命题追踪-存储稀疏矩阵需要保存的信息]
若采用常规的方法存储稀疏矩阵,则相当浪费存储空间,因此仅存储非零元素。但通常非零元素的分布没有规律,所以仅存储非零元素的值是不够的,还要存储它所在的行和列。因此,将非零元素及其相应的行和列构成一个三元组(行标i,列标j,值aᵢ,ⱼ ),如图 3.26 所示。然后按照某种规律存储这些三元组线性表。稀疏矩阵压缩存储后便失去了随机存取特性。
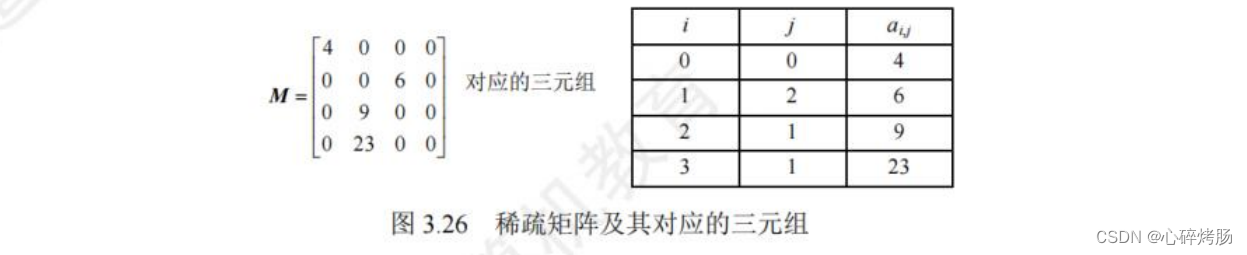
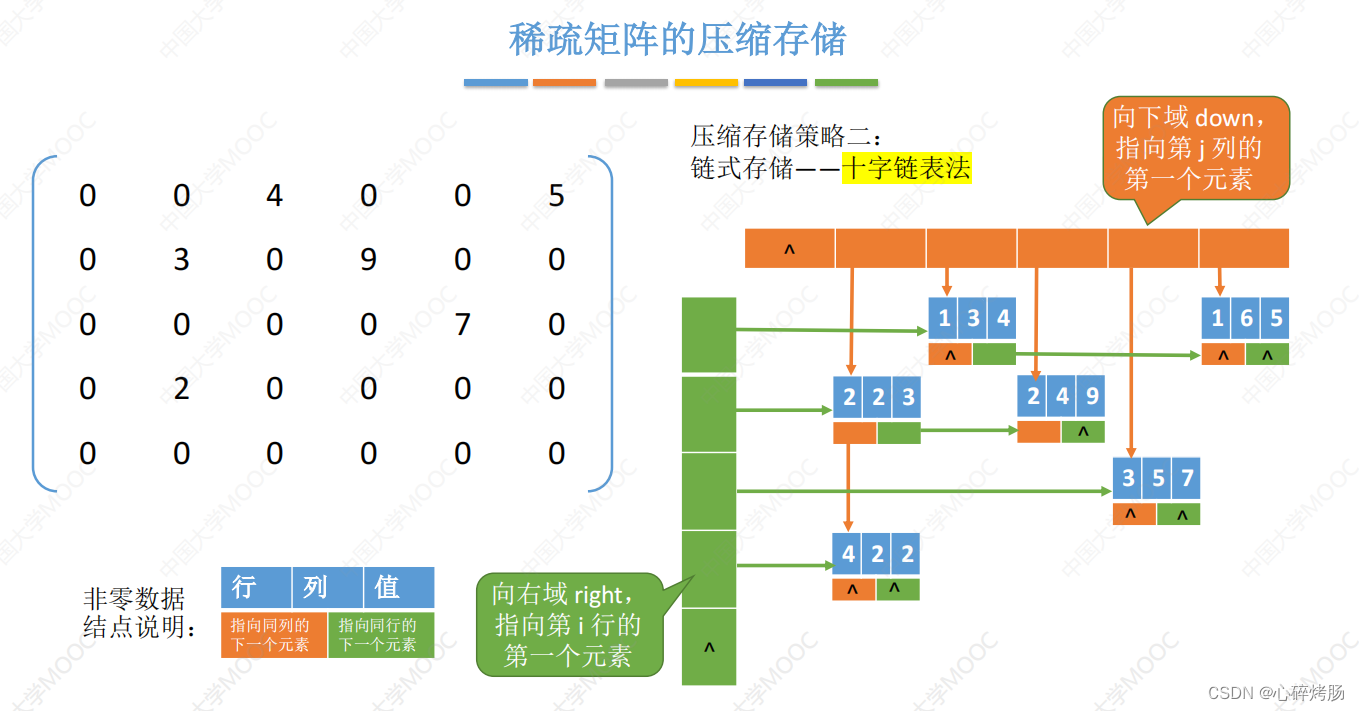
[命题追踪-适合稀疏矩阵压缩存储的存储结构]
稀疏矩阵的三元组表既可以采用数组存储,又可以采用十字链表存储(见6.2节后续讲解)。当存储稀疏矩阵时,不仅要保存三元组表,而且要保存稀疏矩阵的行数、列数和非零元素的个数。
5.知识回顾


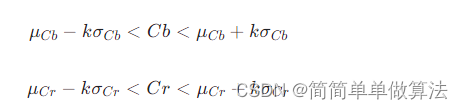


![[RocketMq:基于容器化]:快速部署安装](https://img-blog.csdnimg.cn/direct/88508eb6580d429c878c4e30fda70f97.png)