最小生成树-Prim的延迟实现

理论基础

树的基本性质

用一条边连接树中的任意两个顶点都会产生一个新的环；
从树中删去一条边将会得到两棵独立的树。

切分定理的定义

定义。图的一种切分是将图的所有顶点分为两个非空且不重叠的两个集合。横切边
是一条连接两个属于不同集合的顶点的边。
命题 （切分定理）。在一幅加权图中，给定任意的切分，它的横切边中的权重最
小者必然属于图的最小生成树。

切分定理的证明

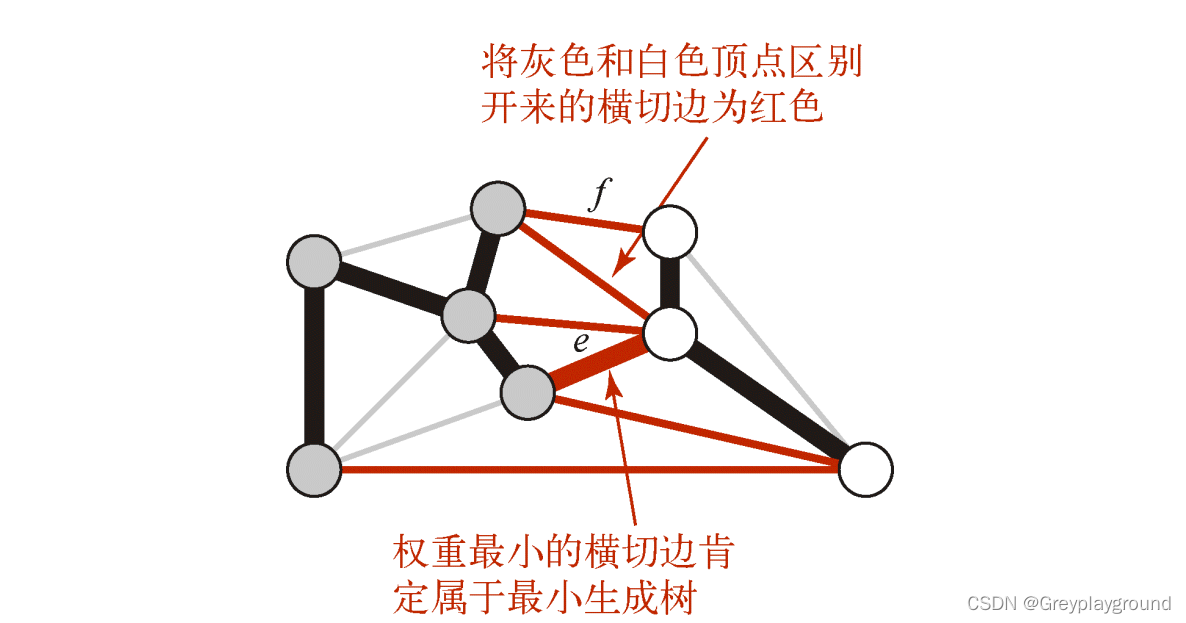
证明。令e为权重最小的横切边,T为图的最小生成树。我们采用反证法：假设T
不包含e。那么如果将e加入T，得到的图必然含有一条经过e的环，且这个环
至少含有另一条横切边——设为f，f的权重必然大于e（因为e的权重是最小的
且图中所有边的权重均不同）。那么我们删掉f而保留e就可以得到一棵权重更
小的生成树。这和我们的假设T矛盾。

实验数据和算法流程

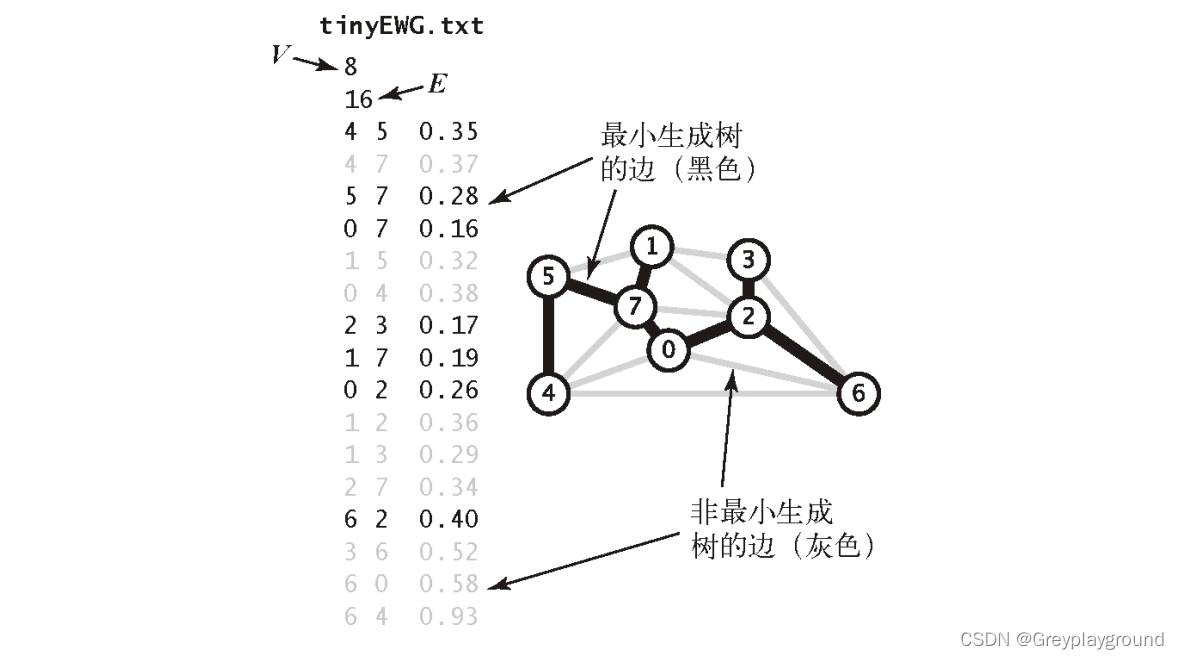
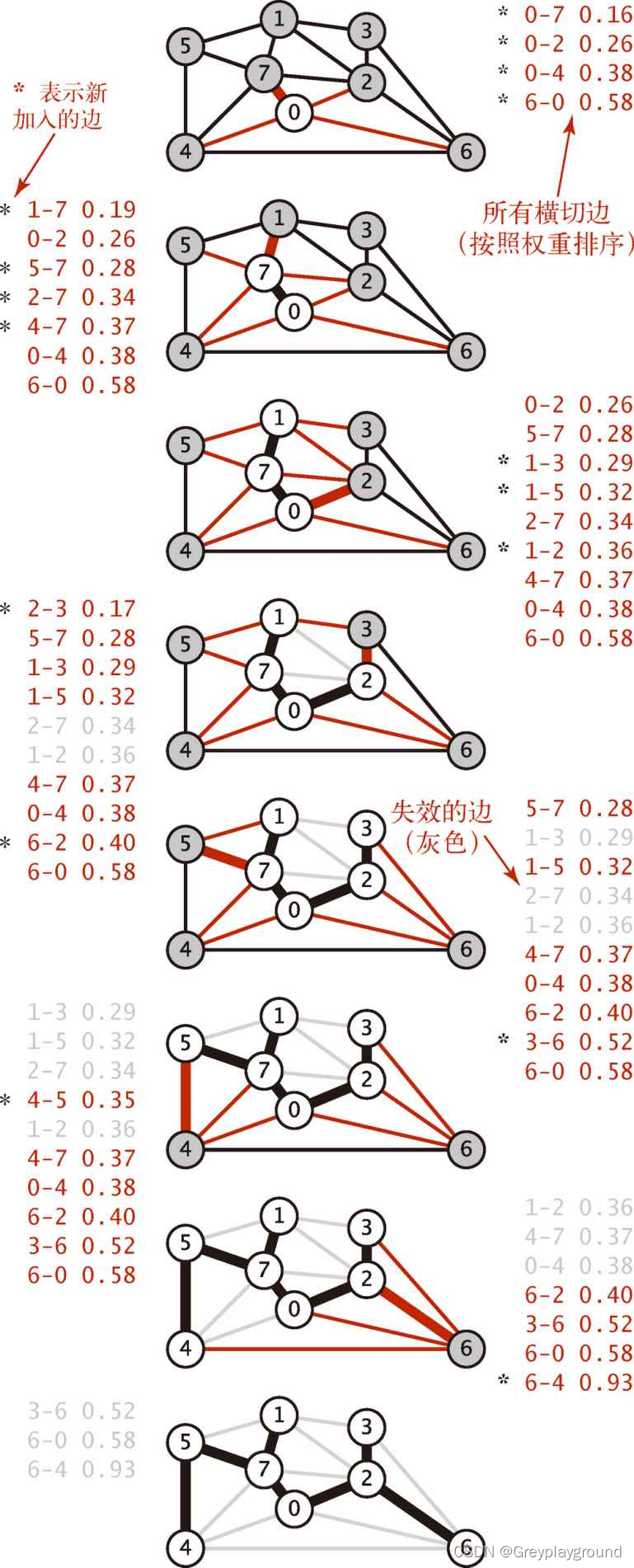
代码实现

import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.myMinPQ;
import edu.princeton.cs.algs4.StdOut;public class myLazyPrimMST {private boolean[] marked;private myLinkedQueue<myEdge> mst;private myMinPQ<myEdge> pq;private double totalWeight;public myLazyPrimMST(myEdgeWeightedGraph G){marked = new boolean[G.V()];mst = new myLinkedQueue<myEdge>();pq = new myMinPQ<myEdge>();visit(G,0);while(!pq.isEmpty()){myEdge e = pq.delMin();int v=e.either();int w=e.other(v);if(marked[v]&&marked[w]) continue;mst.enqueue(e);if(!marked[v]) visit(G,v);if(!marked[w]) visit(G,w);}}private void visit(myEdgeWeightedGraph G, int v){marked[v] = true;for(myEdge e:G.adj(v))if(!marked[e.other(v)])pq.insert(e);}public Iterable<myEdge> edges(){ return mst; }public double weight(){totalWeight = 0.0;for(myEdge e:edges())totalWeight +=e.weight();return totalWeight;}public static void main(String[] args){In in = new In(args[0]);myEdgeWeightedGraph G = new myEdgeWeightedGraph(in);myLazyPrimMST mst = new myLazyPrimMST(G);for(myEdge e:mst.edges())StdOut.println(e);StdOut.print(mst.weight());}
}

代码详解

这段代码实现了一个名为 myLazyPrimMST 的类，用于计算加权无向图的最小生成树（MST），采用的是 Prim 的延迟算法。下面是代码的主要功能和操作步骤的详细解释：

1. 类变量：
   • private boolean[] marked;：标记数组，用于记录图的顶点是否已被访问。
   • private myLinkedQueue<myEdge> mst;：用于存储构成最小生成树的边。
   • private myMinPQ<myEdge> pq;：优先队列，用于按边的权重顺序访问边。
   • private double totalWeight;：记录最小生成树的总权重。
2. 构造函数：
   • 在构造最小生成树时，首先初始化标记数组、边队列和优先队列。
   • 从顶点0开始访问图，将其相邻的未访问边加入优先队列。
   • 循环从优先队列中取出最小边，如果这条边的两个顶点已经被标记，则忽略此边；否则，将其加入到生成树中，并访问相邻的未标记顶点。
3. 访问顶点（visit 方法）：
   • 标记顶点为已访问。
   • 遍历与顶点相连的所有边，如果边的另一端未被标记，则将该边加入优先队列。
4. 获取生成树的边和权重：
   • edges() 方法返回构成最小生成树的边。
   • weight() 方法计算最小生成树的总权重，通过遍历所有生成树的边并累加它们的权重。
5. 主函数：
   • 从文件读取图的数据构造图对象。
   • 创建 myLazyPrimMST 对象来生成最小生成树。
   • 输出生成树的所有边和总权重。

通过这种方式，myLazyPrimMST 类使用延迟的 Prim 算法有效地找到了一个给定图的最小生成树，这种算法特别适合处理稀疏图。

实验

代码编译

$ javac myLazyPrimMST.java

代码运行

代码运行输出的是计算得到的最小生成树的所有边，以及最小生成树所有边的总权重

$ java myLazyPrimMST ..\data\tinyEWG.txt
0-7 0.16
1-7 0.19
0-2 0.26
2-3 0.17
5-7 0.28
4-5 0.35
6-2 0.40
1.81

参考资料

算法（第四版） 人民邮电出版社