MATLAB中功率谱密度计算pwelch函数使用详解
目录
前言
一、pwelch函数简介
二、pwelch函数参数说明
三、pxx = pwelch(x)示例
四、[pxx,f]=pwelch(x,window,noverlap,nfft,fs)示例
四、[pxx,f] = pwelch(x,window,noverlap,nfft,fs,freqrange,spectrumtype)示例
五、多通道功率谱估计
六、参考资料
总结
前言
详细介绍MATLAB中功率谱密度计算pwelch函数的使用方法,介绍如何使用该函数及输入各个参数的含义,手把手用代码教你学习pwelch函数,文中附有代码,足够pwelch函数入门了。
提示:以下是本篇文章正文内容,希望能帮助到各位,转载请附上链接。
一、pwelch函数简介
MATLAB中的pwelch函数是一种用于快速估计信号功率谱密度的工具,也可以计算信号的功率谱,通过阅读该函数使用说明会发现功率谱和功率谱密度是两个不同的概念,要注意一下,在很多教材上都称功率谱和功率谱密度是同一个概念,这是错的,不要被误导。
pwelch函数可以只对一个信号进行功率谱密度估计,也可以同时对多个信号进行功率谱密度估计,简而言之,就是其输入信号那个参数可以是向量,也可以是矩阵。
二、pwelch函数参数说明
函数说明文档里面pwelch函数调用的句话格式很多,我们不用关心那么多,关心如下几个格式和默认参数是怎么一回事就可以了。
pxx = pwelch(x)
[ pxx, f ] = pwelch(x,window,noverlap,nfft,fs)
[ pxx, f ] = pwelch(x,window,noverlap,nfft,fs,freqrange)
[ pxx, f ] = pwelch(x,window,noverlap,nfft,fs,freqrange,spectrumtype)
x--------输入信号,指定为行向量或列向量,或矩阵。 如果 x 是矩阵,则其列被视为独立通道
noverlap----------重叠样本的数量,指定为小于窗口长度的正整数。 如果省略 noverlap 或 noverlap 指定为空,则使用一个值来获得段之间 50% 的重叠,即默认50%重叠。
nfft--------DFT 点数,指定为正整数。 对于实值输入信号 x(PSD 估计值),如果 nfft 为偶数,则 pxx 的长度为 (nfft/2 + 1);如果 nfft 为奇数,则 pxx 的长度为 (nfft + 1)/2。 对于复值输入信号 x,PSD 估计的长度始终为 nfft。 如果 nfft 指定为空,则使用默认的 nfft。如果 nfft 大于Window长度,则数据用零填充。 如果 nfft 小于Window长度,则使用 datawrap包装该段,使长度等于nfft。建议两者相等。
fs-------采样频率,指定为正标量。 采样率是单位时间内的采样数。 如果时间单位是秒,那么采样率的单位是Hz。
freqrange--------------PSD 估计的频率范围,指定为“单边”、“双边”或“中心”之一。 对于实值信号,默认值为“单侧”;对于复值信号,默认值为“双侧”。 每个选项对应的频率范围为
'oneside' — 返回实值输入信号 x 的单侧 PSD 估计。 如果 nfft 为偶数,则 pxx 的长度为 nfft/2 + 1, 如果 nfft 为奇数,则 pxx 的长度为 (nfft + 1)/2,间隔为 [0,π) rad/sample。 当 fs 可选指定时,对于偶数和奇数长度 nfft,相应的间隔分别为 [0,fs/2] 周期/单位时间和 [0,fs/2) 周期/单位时间。该函数将除 0 和奈奎斯特频率之外的所有频率的功率乘以 2,以保持总功率不变。
'twoside' - 返回实值或复值输入 x 的两侧 PSD 估计值。 在这种情况下,pxx 的长度为 nfft,并在区间 [0,2π) rad/sample 上计算。 当指定fs时,间隔为[0,fs)周期/单位时间。
'centered' - 返回实值或复值输入 x 的中心两侧 PSD 估计值。 在这种情况下,pxx 的长度为 nfft,并且在偶数长度 nfft 的间隔 (–π,π] rad/sample 和奇数长度 nfft 的 (–π,π) rad/sample 区间内计算。当 fs 可选地指定时,相应的对于偶数和奇数长度 nfft,间隔分别为 (–fs/2, fs/2] 周期/单位时间和 (–fs/2, fs/2) 周期/单位时间。
spectrumtype------------功率谱类型,指定为“psd”或“power”之一。 默认“psd”,将返回功率谱密度。 指定“power”可通过窗口的等效噪声带宽来缩放 PSD 的每个估计值。 使用“power”选项可以获得每个频率的功率估计值。
三、pxx = pwelch(x)示例
创建一个角频率为π/4 rad的正弦波,外加N(0,1)白噪声。信号的长度是320个样本。得到其Welch PSD估计。
clc;
clear;
close all;rng defaultn = 0:319;
x = cos(pi/4*n)+randn(size(n));pxx = pwelch(x);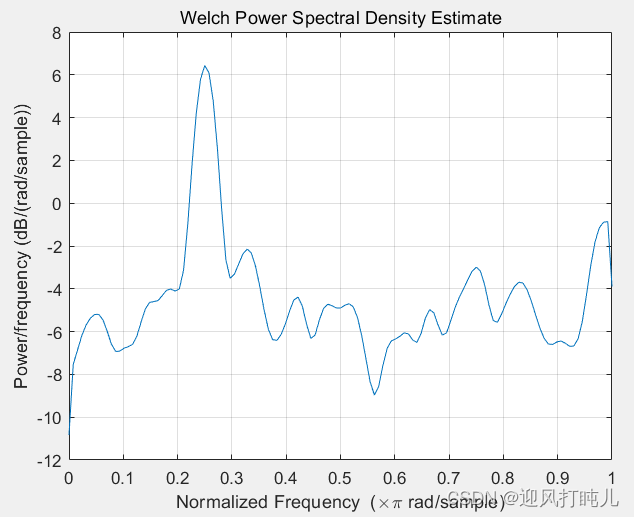
可见,默认横轴是归一化的角频率,纵轴是取了10log10( )的dB功率谱密度。
关于归一化频率,参考:滤波器设计中的频率归一化问题_滤波器归一化频率-CSDN博客
解释如下:
信号处理工具箱中经常使用的频率是Nyquist频率,它被定义为采样频率的一半,在滤波器的结束选择和设计当中的截止频率均使用Nyquist频率进行归一化处理。
例如,对于一个采样频率为1000Hz的系统,300Hz的归一化即为300/500=0.6。归一化频率的范围在[0,1]之间。如果要将归一化频率转换为角频率,则将归一化频率乘以pi;如果将归一化频率转换成Hz,则将归一化频率乘以采样频率的一半。
采样率的一半是最高频率,认为是1,那么真实频率和最高频率的比值就是归一化频率!也叫数字频率。
将信号分成长度为nsc=⌊Nx/4.5⌋。这个动作相当于将信号分成尽可能长的段,以获得接近但不超过8个重叠50%的段。使用汉明窗口显示各部分。指定相邻部分之间50%的重叠
要计算FFT,使用max(256,2^p),其中p=[log2nsc⌉。
Nx = length(x);
nsc = floor(Nx/4.5);
nov = floor(nsc/2);
nff = max(256,2^nextpow2(nsc));t = pwelch(x,hamming(nsc),nov,nff);maxerr = max(abs(abs(t(:))-abs(pxx(:))))

默认分成8段,每段的长度为Nx/4.5=320/4.5=71.1111,舍去多余的数据,分段长度为71,并用同等长度的汉明窗;重叠长度为50%,则nov=floor(71/2)=35;DFT的点数取每段长度最接近的2的整数次幂和256的最大值,最接近的2的整数次幂是比每段长度长的最接近的2的整数次幂,所以DFT计算的时候如果DFT点数大于每段长度。会自动补0。
对于实值信号,默认值为“单侧”PSD,所以计算DFT点数为256,估计的PSD长度只有256/2+1=129点的长度。
四、[pxx,f]=pwelch(x,window,noverlap,nfft,fs)示例
创建一个由100Hz正弦波和加性N(0,1)白噪声组成的信号。采样率为1khz,信号持续时间为5秒。使用500个样本和300个重叠样本的段长度,使用500个DFT点。
clc;
clear;
close all;rng defaultfs = 1000;
t = 0:1/fs:5-1/fs;
x = cos(2*pi*100*t) + randn(size(t));[pxx,f] = pwelch(x,500,300,500,fs);plot(f,10*log10(pxx))xlabel('Frequency (Hz)')
ylabel('PSD (dB/Hz)')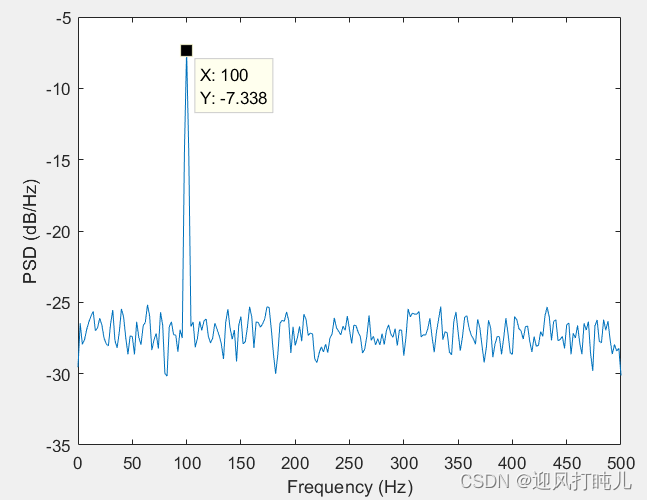
sum(abs(x).^2)/length(x) %信号功率
P = fs/2/length(pxx) * (sum(pxx) - 0.5*(pxx(1) + pxx(end))) %梯形法积分
验证功率,对功率谱密度积分发现和信号功率几乎相等。
增大点数
clc;
clear;
close all;rng defaultfs = 10000;
t = 0:1/fs:5-1/fs;
x = cos(2*pi*100*t) + randn(size(t));[pxx,f] = pwelch(x,5000,3000,5000,fs);plot(f,10*log10(pxx))xlabel('Frequency (Hz)')
ylabel('PSD (dB/Hz)')sum(abs(x).^2)/length(x) %信号功率
P = fs/2/length(pxx) * (sum(pxx) - 0.5*(pxx(1) + pxx(end))) %梯形法积分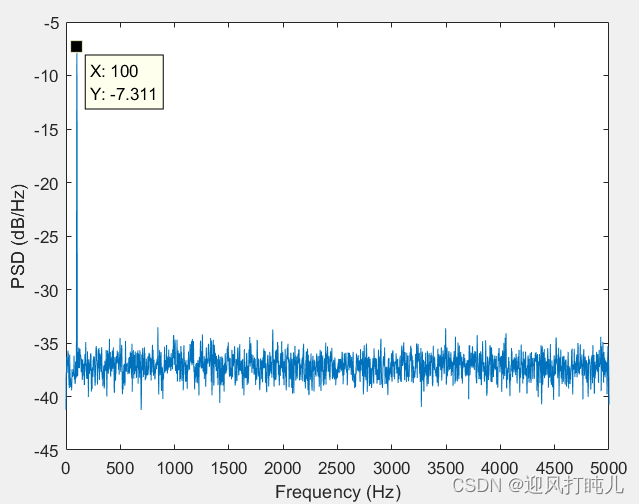

增大段长度,会发现功率谱估计的准,功率谱密度积分的值更接近信号的功率。
四、[pxx,f] = pwelch(x,window,noverlap,nfft,fs,freqrange,spectrumtype)示例
创建一个由100Hz正弦波和加性N(0,1)白噪声组成的信号。采样率为1khz,信号持续时间为5秒。使用500个样本和300个重叠样本的段长度,使用500个DFT点。
clc;
clear;
close all;rng defaultfs = 1000;
t = 0:1/fs:10-1/fs;x = cos(2*pi*100*t)+randn(size(t))+1;[pxx,f] = pwelch(x,500,300,500,fs,'centered');plot(f,10*log10(pxx))
xlabel('Frequency (Hz)')
ylabel('PSD (dB/Hz)')
E=sum(abs(x).^2) %信号能量
P=sum(abs(x).^2)/length(x) %信号功率
P = fs/length(pxx) * (sum(pxx) - 0.5*(pxx(1) + pxx(end))) %梯形法积分�[pxx,f] = pwelch(x,500,300,500,fs,'centered','power');
figure(2)
plot(f,10*log10(pxx))
xlabel('Frequency (Hz)')
ylabel('Magnitude (dB)')
grid使用参数centered得到双边功率谱密度:
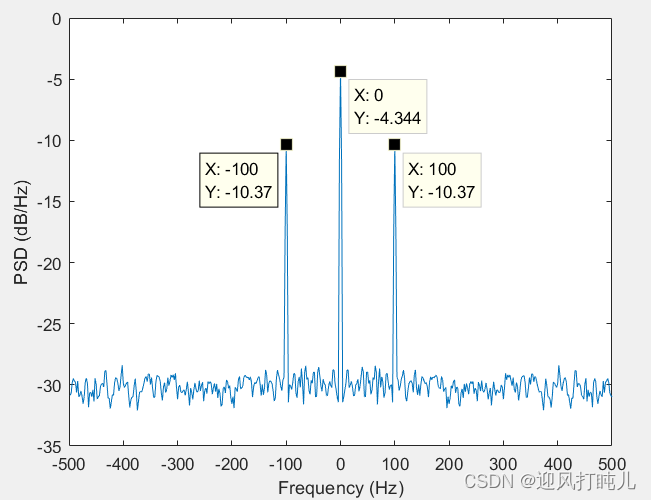
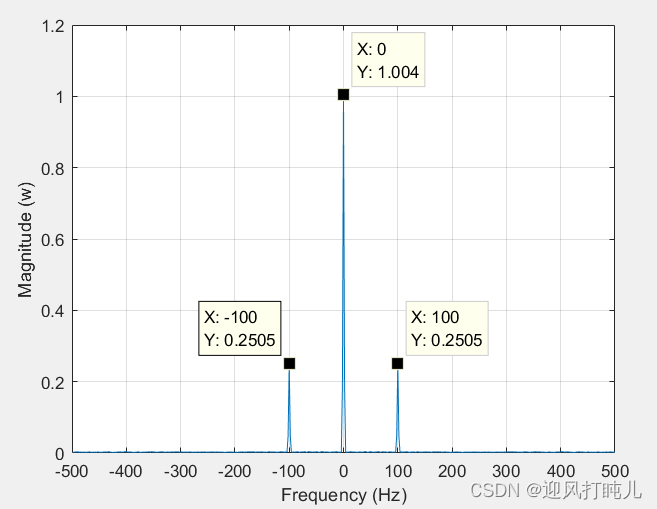
使用参数power得到双边功率谱(不是双边功率谱密度):
观察图可知,与信号设置的功率吻合。
取对数画出如下:
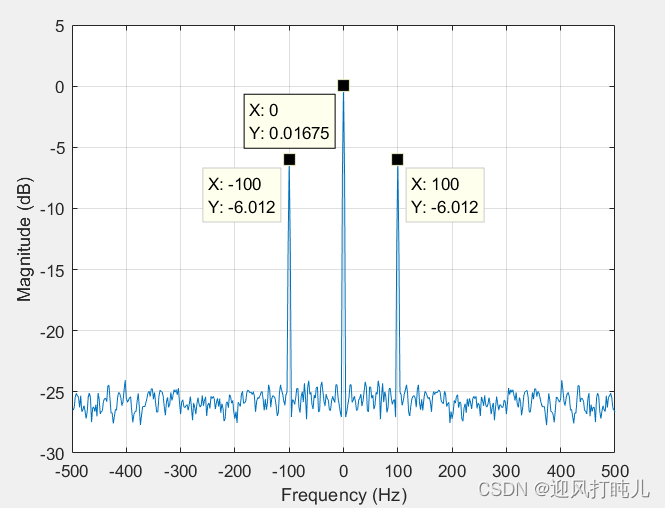

可见,将功率谱密度积分和信号功率相等;观察功率谱图可知,每个频率对应的点显示了该频点的功率大小。
五、多通道功率谱估计
在加性N(0,1)高斯白噪声中生成由三个正弦波组成的多通道信号的1024个样本。正弦波的频率分别为100、200、300Hz,采样频率为1000Hz。使用Welch的方法估计信号的PSD并绘制它。
clc;
clear;
close all;rng defaultfs = 1000;
t = 0:1/fs:5-1/fs;
f = [100;200;300];
x = cos(2*pi*f*t)' + randn(length(t),3);[pxx,f] = pwelch(x,500,300,500,fs);plot(f,10*log10(pxx));xlabel('Frequency (Hz)')
ylabel('PSD (dB/Hz)')
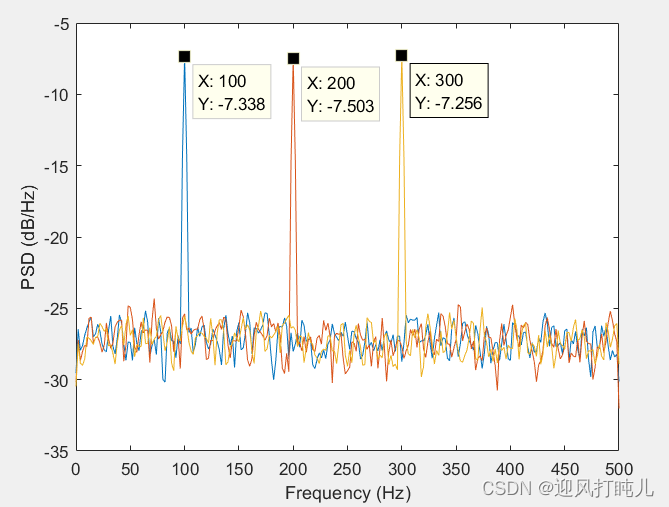
六、参考资料
Welch’s power spectral density estimate - MATLAB pwelch- MathWorks 中国
https://download.csdn.net/download/m0_66360845/89084990![]() https://download.csdn.net/download/m0_66360845/89084990
https://download.csdn.net/download/m0_66360845/89084990
总结
以上就是今天要讲的内容,本文仅仅简单介绍了功率谱密度(功率谱)绘制函数pwelch函数的使用,希望对各位小伙伴有所帮助。




![[数据结构]———归并排序](https://img-blog.csdnimg.cn/direct/c6d4a450684449d0ac5cf1e14e89cca7.png)