1.直接用递推:

下面是AC代码“:
#include<bits/stdc++.h>
using namespace std;
const int N=2010,mod=1e9+7;
int a[N][N];
void init()
{for(int i=0;i<N;i++){for(int j=0;j<=i;j++){if(j==0) a[i][j]=1;else a[i][j]=(a[i-1][j]+a[i-1][j-1])%mod;}}
}
int main()
{init();int n;cin>>n;while(n--){int a1,b;scanf("%d%d",&a1,&b);printf("%d\n",a[a1][b]);}
}2.预处理阶乘:

下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
const int N=100010,mod=1e9+7;
typedef long long LL;
int fact[N],infact[N];
int qq(int a,int k,int p)
{int res=1;while(k){if(k&1) res=(LL)res*a%p;a=(LL)a*a%p;k>>=1;}return res;
}
int main()
{fact[0]=infact[0]=1;for(int i=1;i<N;i++){fact[i]=(LL)fact[i-1]*i%mod;infact[i]=(LL)infact[i-1]*qq(i,mod-2,mod)%mod;}int n;cin>>n;while(n--){int a,b;scanf("%d%d",&a,&b);printf("%d\n",(LL)fact[a]*infact[b]%mod*infact[a-b]%mod);}
}3.卢卡斯定理:

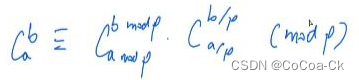
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int p;
int qmi(int a,int k)
{int res=1;while(k){if(k&1) res=(LL)res*a%p;a=(LL)a*a%p;k>>=1;}return res;
}
int C(int a,int b)
{int res=1;for(int i=1,j=a;i<=b;i++,j--){res=(LL)res*j%p;res=(LL)res*qmi(i,p-2)%p;}return res;
}
int lu(LL a,LL b)
{if(a<p&&b<p) return C(a,b);return (LL)C(a%p,b%p)*lu(a/p,b/p)%p;
}
int main()
{int n;cin>>n;while(n--){LL a,b;cin>>a>>b>>p;cout<<lu(a,b)<<endl;}
}4.分解质因数+高精度:

那么如何求阶乘的质因数?
我们先把5000范围里的素数筛出来,然后对于一个素数[a/p]+[a/p^2]+...即可,这样我们就把组合数转换成了质因数,再高精度乘法即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
const int N=5010;
int prime[N],cnt;
bool st[N];
int sum[N];
void init(int n)
{for(int i=2;i<=n;i++){if(!st[i]) prime[cnt++]=i;for(int j=0;prime[j]<=n/i;j++){st[prime[j]*i]=1;if(i%prime[j]==0) break; }}
}
int get(int n,int p)//n!中p的个数
{int res=0;while(n){res+=n/p;n/=p;}return res;
}
vector<int> mul(vector<int> a,int b)
{vector<int> c;int t=0;for(int i=0;i<a.size();i++){t+=a[i]*b;c.push_back(t%10);t/=10;}while(t){c.push_back(t%10);t/=10;}return c;
}
int main()
{int a,b;cin>>a>>b;init(a);for(int i=0;i<cnt;i++){int p=prime[i];sum[i]=get(a,p)-get(b,p)-get(a-b,p);}//把所有质因子乘骑来vector<int> res;res.push_back(1);for(int i=0;i<cnt;i++){for(int j=0;j<sum[i];j++){res=mul(res,prime[i]);}}for(int i=res.size()-1;i>=0;i--) printf("%d",res[i]);
}5.卡特兰数

这样我们把序列转化成了一条条路径:
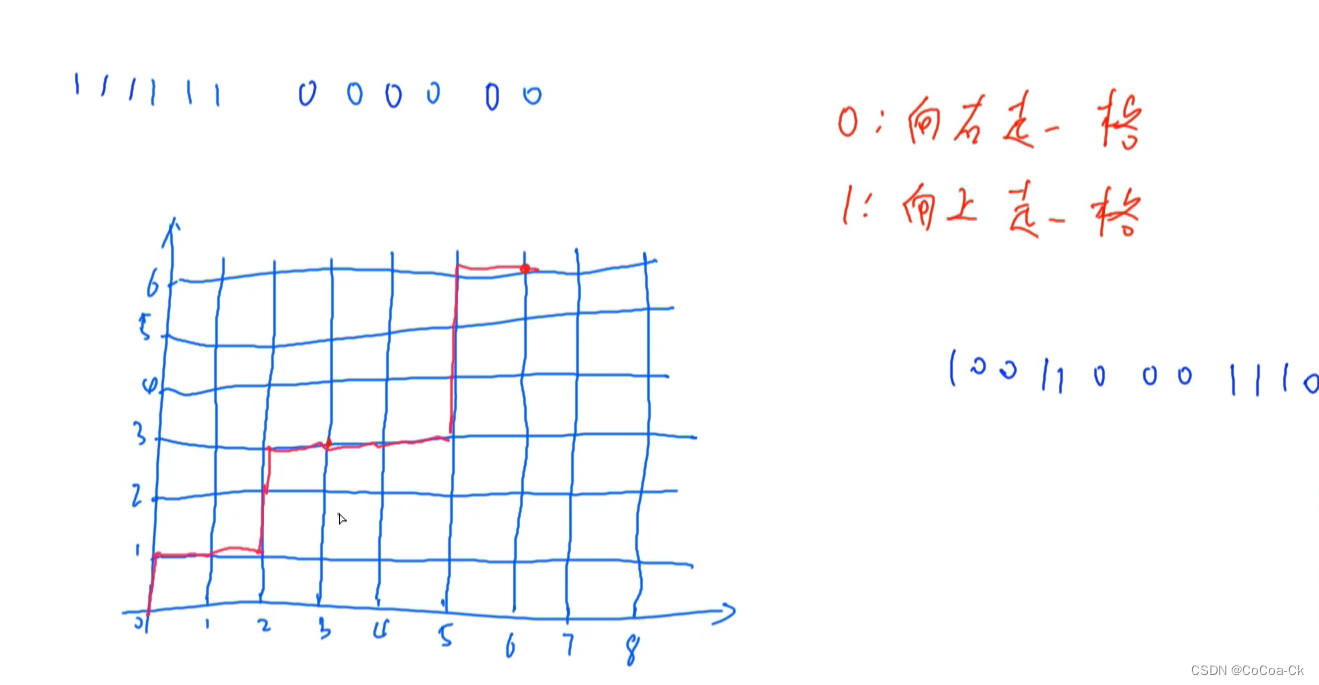
同时要满足条件:始终在y=x的下面,不可以与y=x+1有接触
我们找到第一次交的点,把后面的关于y=x+1对称,最终一定到(n-1,n+1)。
答案就是(2n,n-C2n,n-1,化简就是C2n,n/(n+1)




![正点原子[第二期]Linux之ARM(MX6U)裸机篇学习笔记-9.1-LED灯(模仿STM32驱动开发实验)](https://img-blog.csdnimg.cn/direct/7ec638eebccc46c0b66e3859f0454c1a.png)
![[每日AI·0501]GitHub 版 Devin,Transformer的强力挑战者 Mamba,Sora 制作细节与踩坑,OpenAI 记忆功能](https://img-blog.csdnimg.cn/img_convert/185ea0ff328394d2d377a1344a6078d1.png)