1. 介绍
每个激活函数的输入都是一个数字,然后对其进行某种固定的数学操作。激活函数给神经元引入了非线性因素,如果不用激活函数的话,无论神经网络有多少层,输出都是输入的线性组合。激活函数的意义在于它能够引入非线性特性,使得神经网络可以拟合非常复杂的函数,从而提高了神经网络的表达能力和预测性能。
激活函数的发展经历了Sigmoid -> Tanh -> ReLU -> Leaky ReLU -> Maxout这样的过程,还有一个特殊的激活函数Softmax,因为它只会被用在网络中的最后一层,用来进行最后的分类和归一化。
具体来说,激活函数的作用有以下几个方面:
-
引入非线性特性:激活函数能够将神经元的输入信号转换为输出信号,从而引入非线性特性,使得神经网络可以拟合非常复杂的函数。
-
压缩输出范围:激活函数能够将神经元的输出范围压缩到一定的范围内,这有助于防止神经元输出的值过大或过小,从而提高了神经网络的稳定性和泛化性能。
-
增加网络深度:激活函数能够增加神经网络的深度,从而提高了神经网络的表达能力和预测性能。
-
改善梯度消失问题:激活函数能够改善神经网络中的梯度消失问题,从而提高了神经网络的训练效率和收敛速度。
2. 特性
sigmoid函数
import numpy as npdef sigmiod(x):return 1. / (1. + np.exp(-x))
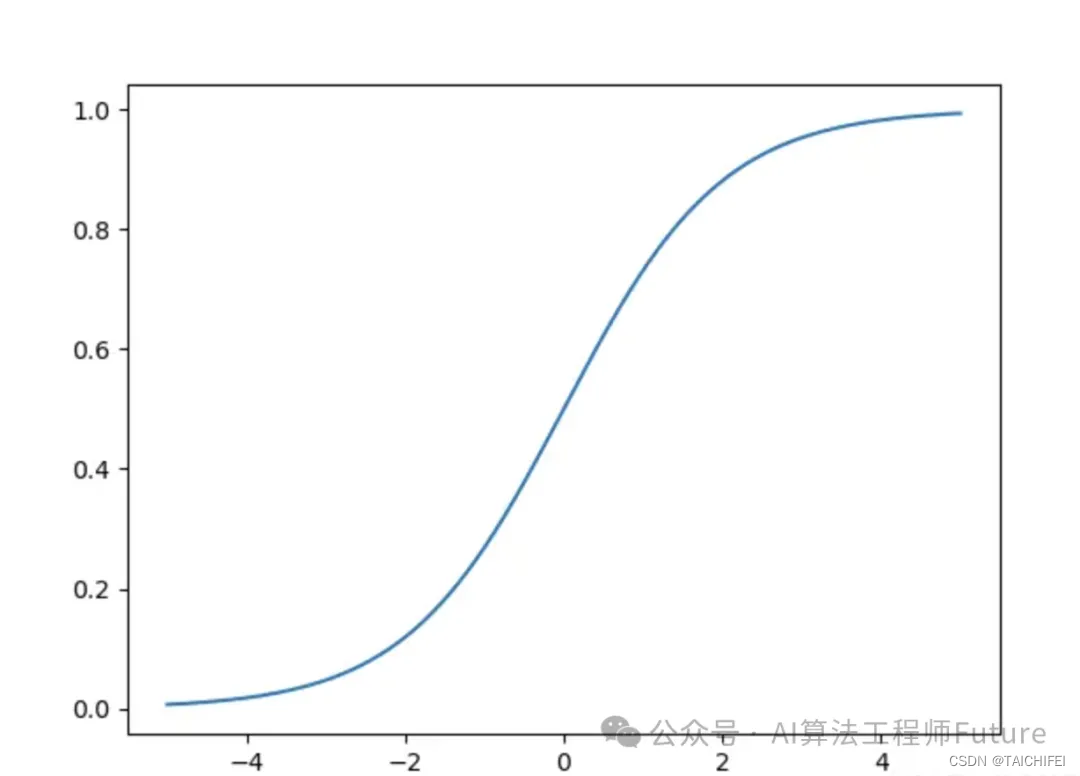
sigmoid函数是神经网络中最早也是最常用的激活函数之一,它的特点是将输入值映射到0到1之间的连续范围内,输出值具有良好的可解释性,但是它在梯度消失和输出饱和等问题上表现不佳。
Tanh
import numpy as npdef tanh(x):return np.tanh(x)
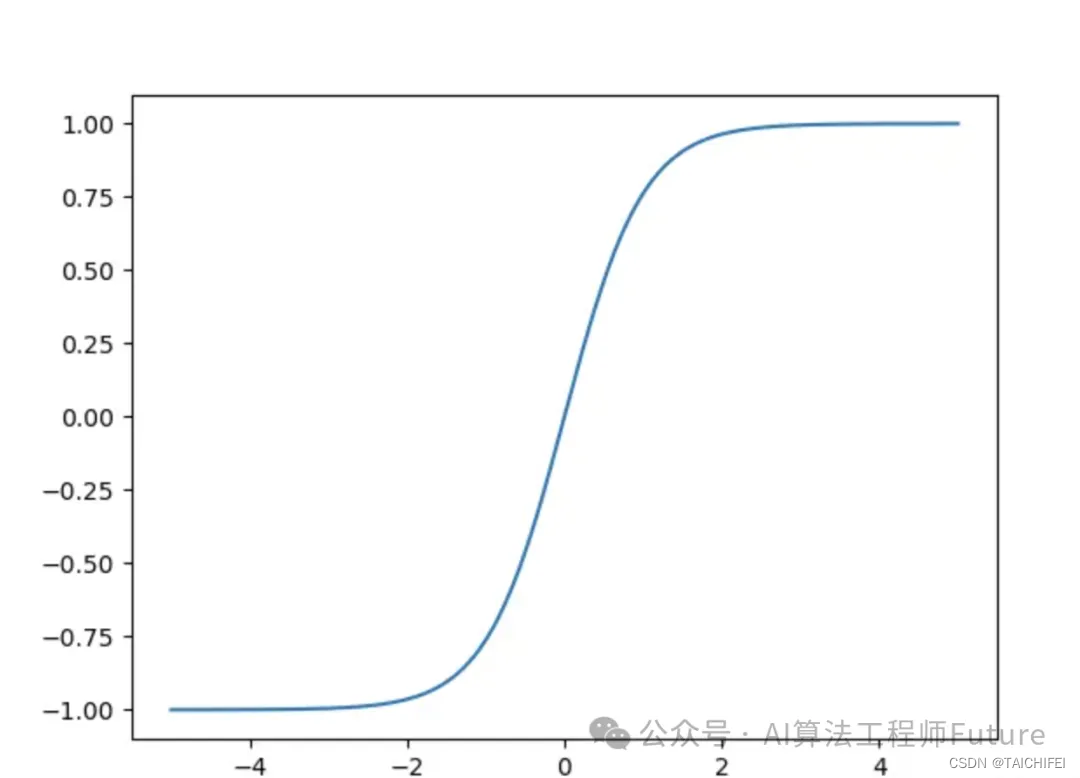
Tanh(双曲正切)函数是一种常用的激活函数,其数学定义为 f ( x ) = e x − e − x e x + e − x f(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} f(x)=ex+e−xex−e−x ( f ( x ) = ( e x p ( x ) − e x p ( − x ) ) / ( e x p ( x ) + e x p ( − x ) ) f(x) = (exp(x) - exp(-x)) / (exp(x) + exp(-x)) f(x)=(exp(x)−exp(−x))/(exp(x)+exp(−x)))。它的输出范围是 (-1, 1),在输入接近正无穷时趋于1,在接近负无穷时趋于-1,在接近0时趋于0。在神经网络中,Tanh函数通常用于隐藏层的激活函数。
Tanh函数是一种具有S形状的激活函数,其特点是将输入值映射到-1到1之间的连续范围内,输出值也具有良好的可解释性。Tanh解决了Sigmoid的输出是不是零中心的问题,Tanh函数在某些情况下可以表现出色,但是它也存在梯度消失和输出饱和等问题,因此在深度神经网络中使用并不广泛。
ReLU函数
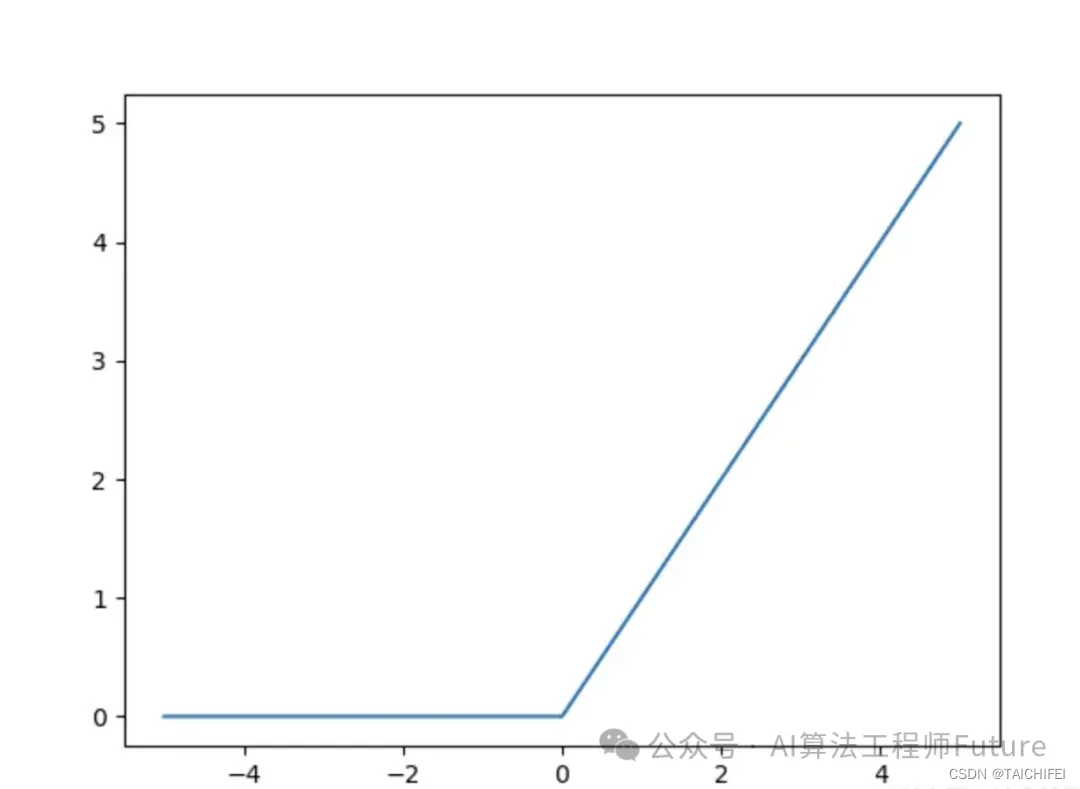
import numpy as npdef ReLU(x):return np.maxinum(0, x)ReLU函数是当前最常用的激活函数之一,它的特点是简单、快速,并且在许多情况下表现出色。ReLU函数将负数输入映射到0,将正数输入保留不变,因此在训练过程中可以避免梯度消失的问题。
但是ReLU函数在输入为负数时输出为0,这可能导致神经元死亡,ReLU单元比较脆弱并且可能“死掉”,而且是不可逆的,因此导致了数据多样化的丢失。通过合理设置学习率,会降低神经元“死掉”的概率。因此后续的改进版本LeakyReLU得到了广泛的应用。
LeakyReLU函数
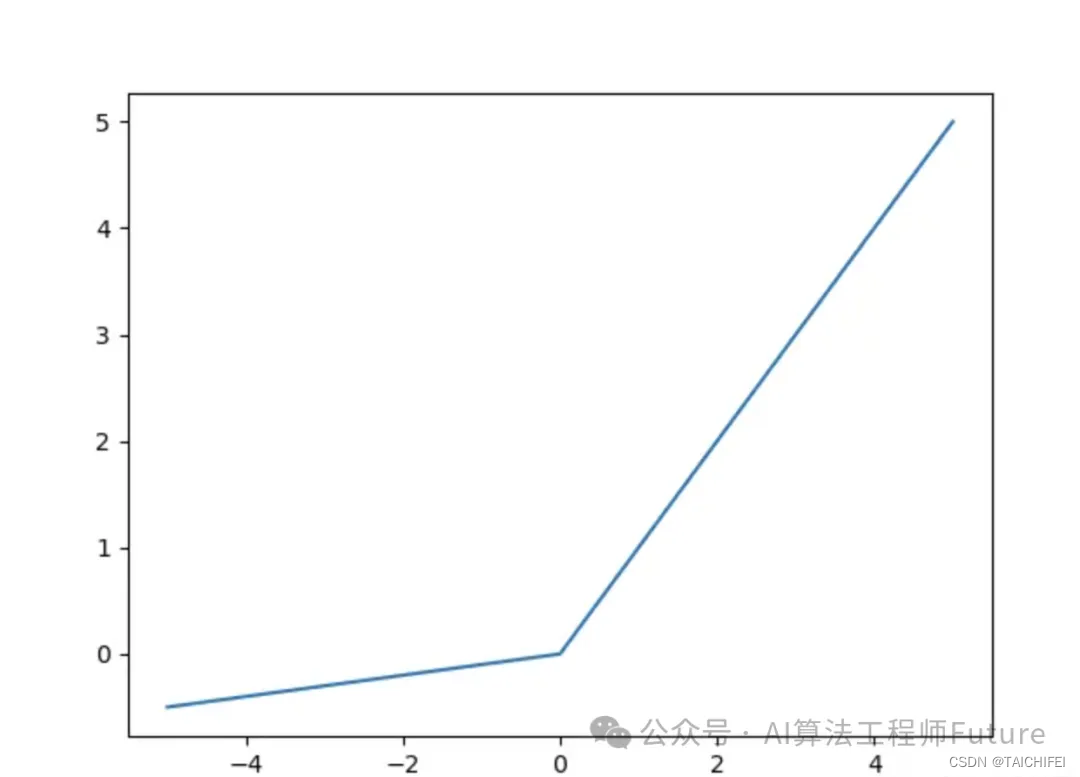
def LeakyReLU(x, alpha=0.1):return np.maxinum(alpha*x, x)def LeakyReLU(x, alpha=0.01):return x if x > 0 else alpha * xLeakyReLU函数是ReLU函数的改进版本,它在输入为负数时输出一个小的负数,从而避免了ReLU函数可能导致神经元死亡的问题。LeakyReLU函数的优点是简单、快速,并且在许多情况下表现出色,但是其超参数需要手动调整,因此在实际应用中需要进行一定的调试。
Maxout
import numpy as npdef maxout(x, weights, biases):output1 = np.dot(x, weights[0] + biases[0])output2 = np.dot(x, weights[1]+ biases[1])return np.maximum(output1, output2)
x = np.array([1.0, 2.0, 3.0])
weights = [np.array([0.5, 0.3, 0.2]), np.array([0.4, 0.5, 0.6])]
biases = [0.1, 0.2]
print(maxout(x, weights, biases))
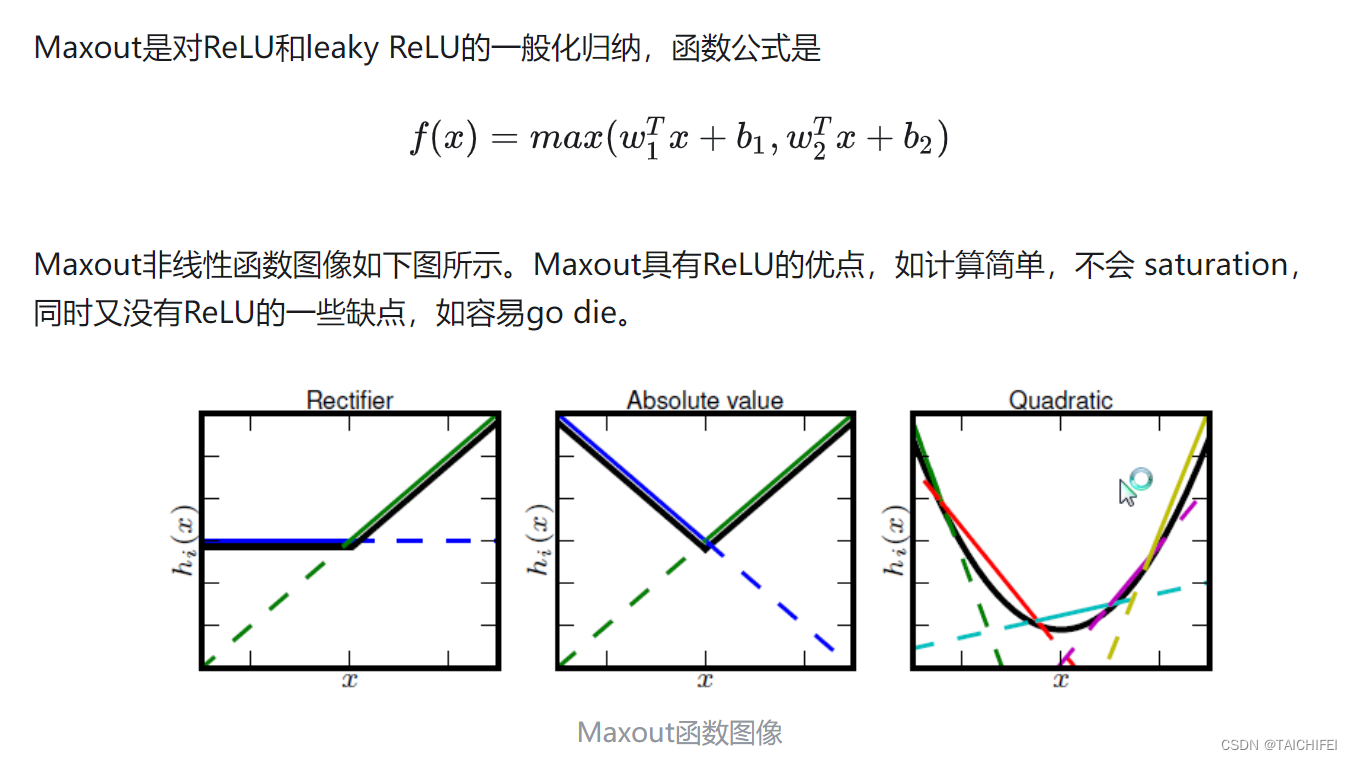
每个神经元的参数double,这就导致整体参数的数量激增。
Softmax函数
import numpy as npdef Softmax(x):exp_x = np.exp(x)return exp_x / np.sum(exp_x, axis=0, keepdims=True)# 测试
x = np.array([1.0, 2.0, 3.0])
print(Softmax(x)) # 输出 [0.09003057 0.24472847 0.66524096]
import torchdef Softmax(x):exp_x = torch.exp(x)return exp_x / torch.sum(exp_x, dim=0, keepdim=True)# 测试
x = torch.tensor([1.0, 2.0, 3.0])
print(Softmax(x)) # 输出 [0.09003057 0.24472847 0.66524096]

Softmax函数是一种常用于多分类问题的激活函数,它将输入值映射到0到1之间的概率分布,可以将神经网络的输出转换为各个类别的概率值。Softmax函数的优点是简单、易于理解,并且在多分类问题中表现出色,但是它也存在梯度消失和输出饱和等问题。
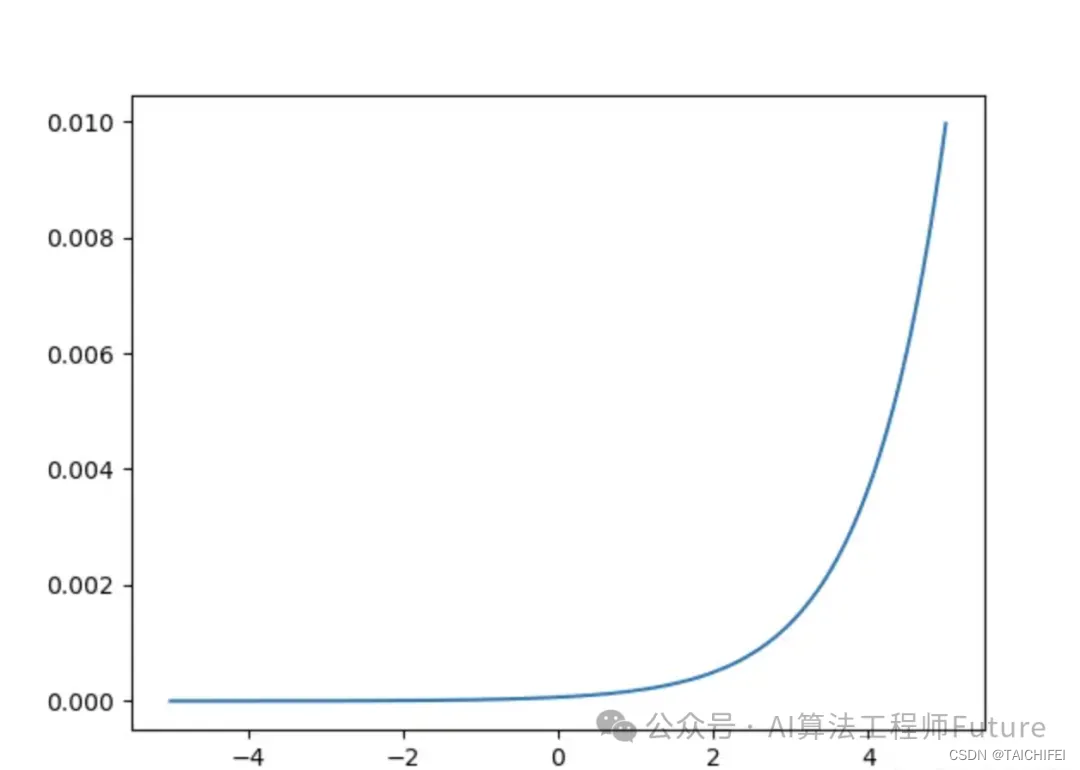
GELU函数
def GELU(x):cdf = 0.5 * (1.0 + np.tanh(np.sqrt(2 / np.pi)) * (x + 0.044715 * np.power(x, 3)))return x * cdfprint(GELU(0)) # 输出 0.0
print(GELU(1)) # 输出 0.8413447460685429
print(GELU(-1)) # 输出 -0.15865525393145707
GELU函数是一种近年来提出的激活函数,它的特点是在ReLU函数的基础上引入了高斯误差线性单元,从而在某些情况下能够表现出色。GELU函数具有平滑的非线性特性,可以避免ReLU函数可能导致的神经元死亡问题。

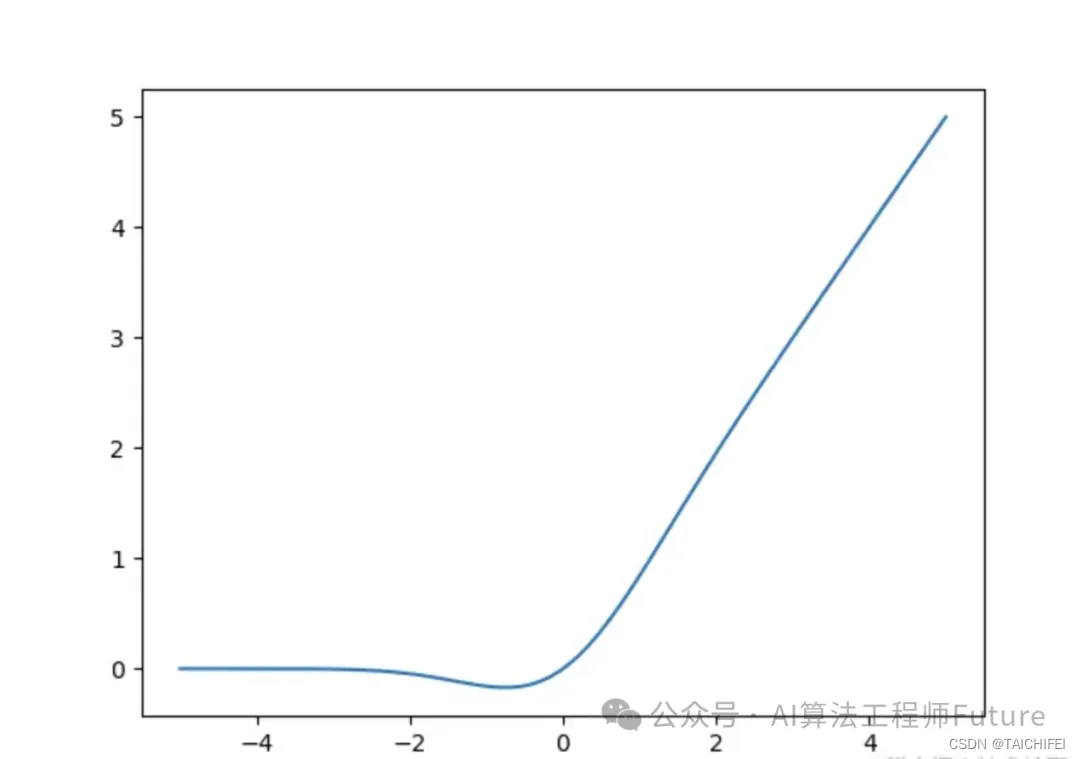
GELU函数是一种近年来提出的激活函数,它的特点是在ReLU函数的基础上引入了高斯误差线性单元,从而在某些情况下能够表现出色。GELU函数具有平滑的非线性特性,可以避免ReLU函数可能导致的神经元死亡问题。
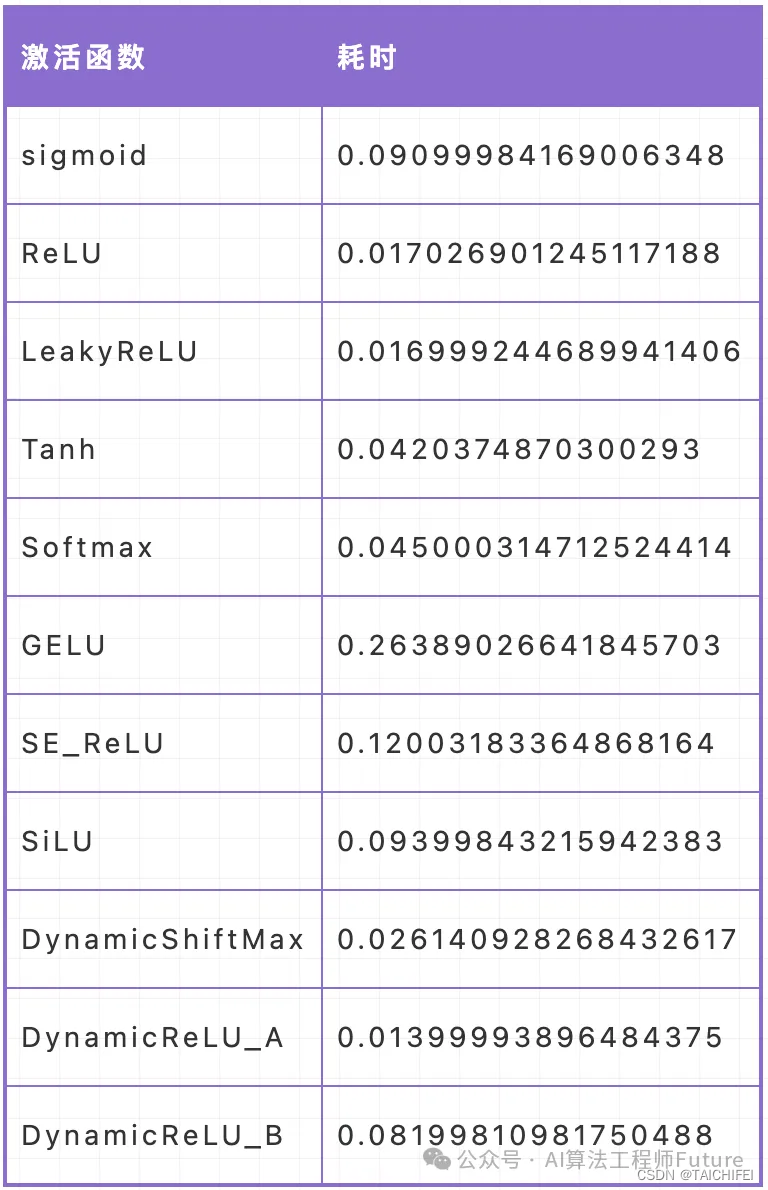
性能测试
我们采用控制变量法进行激活函数的推理速度测试,x为输入,范围为-1到1之间的十万个数据,运行次数为100计算激活函数的计算耗时。
参考:
https://zhuanlan.zhihu.com/p/32610035
https://mp.weixin.qq.com/s/8pZ1IH_WoFG-QCjOztdc5Q