同时取送货的车辆路径问题VRPSDP的数学模型如下:
模型假设
- 所有车辆的载重、容量等性能相同。
- 每个客户的需求(送货和取货量)是已知的,且在服务过程中不会改变。
- 车辆的行驶速度恒定,不考虑交通拥堵等实时路况变化。
- 每个客户点只能被访问一次,且必须被访问。
- 配送中心有足够的货物满足所有送货需求,且有足够的容量存储所有取回的货物。
模型描述
参数和变量定义
- C: 客户集合
- V: 车辆集合
- Q: 车辆的载重能力
: 客户点i 到客户点j的距离
: 客户点i的送货量
: 客户点i的取货量
: 若车辆k从客户点i行驶到客户点j,则为1;否则为0
: 若车辆k服务客户点i,则为1;否则为0
: 车辆 k 在服务完客户点 i 后的载货量
目标函数
最小化总行驶距离:
约束条件
- 车辆从配送中心出发并最终返回配送中心:
- 每个客户点只能被一辆车服务一次:
- 车辆载重约束:
- 货物装载和卸载的连续性:
- 确保取货和送货的操作:
如果,则必须满足客户点i的取货和送货需求。
我们用MATLAB实现以下一个小算例的模型优化:
车速v=40km/h, 车辆载重Q=15t, 同时送取货的需求点的数据如下表所示:
| 客户点 | x | y | 送货需求量/吨 | 取货需求量/吨 |
| 0 | 10 | 10 | 0 | 0 |
| 1 | 17 | 7 | 2 | 2 |
| 2 | 17 | 11 | 2.5 | 2.5 |
| 3 | 3 | 12 | 4 | 1.5 |
| 4 | 8 | 1 | 3.5 | 2 |
| 5 | 14 | 14 | 4 | 5 |
| 6 | 7 | 0 | 0 | 2 |
| 7 | 5 | 6 | 3.5 | 2.5 |
| 8 | 19 | 17 | 2.5 | 3.5 |
| 9 | 11 | 7 | 1.5 | 5 |
| 10 | 1 | 17 | 4.5 | 2 |
部分MATLAB主程序如下:


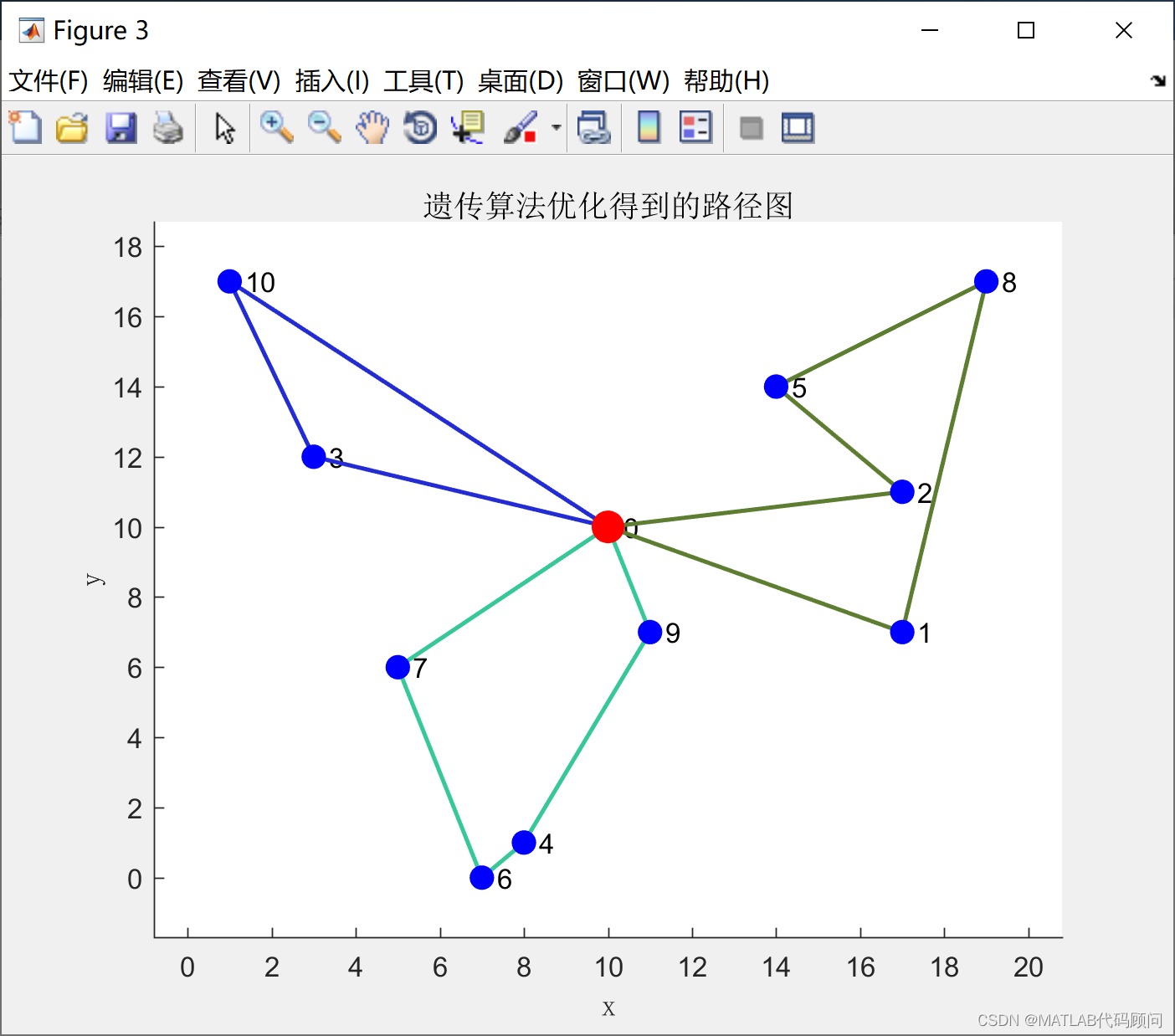
程序结果如下:
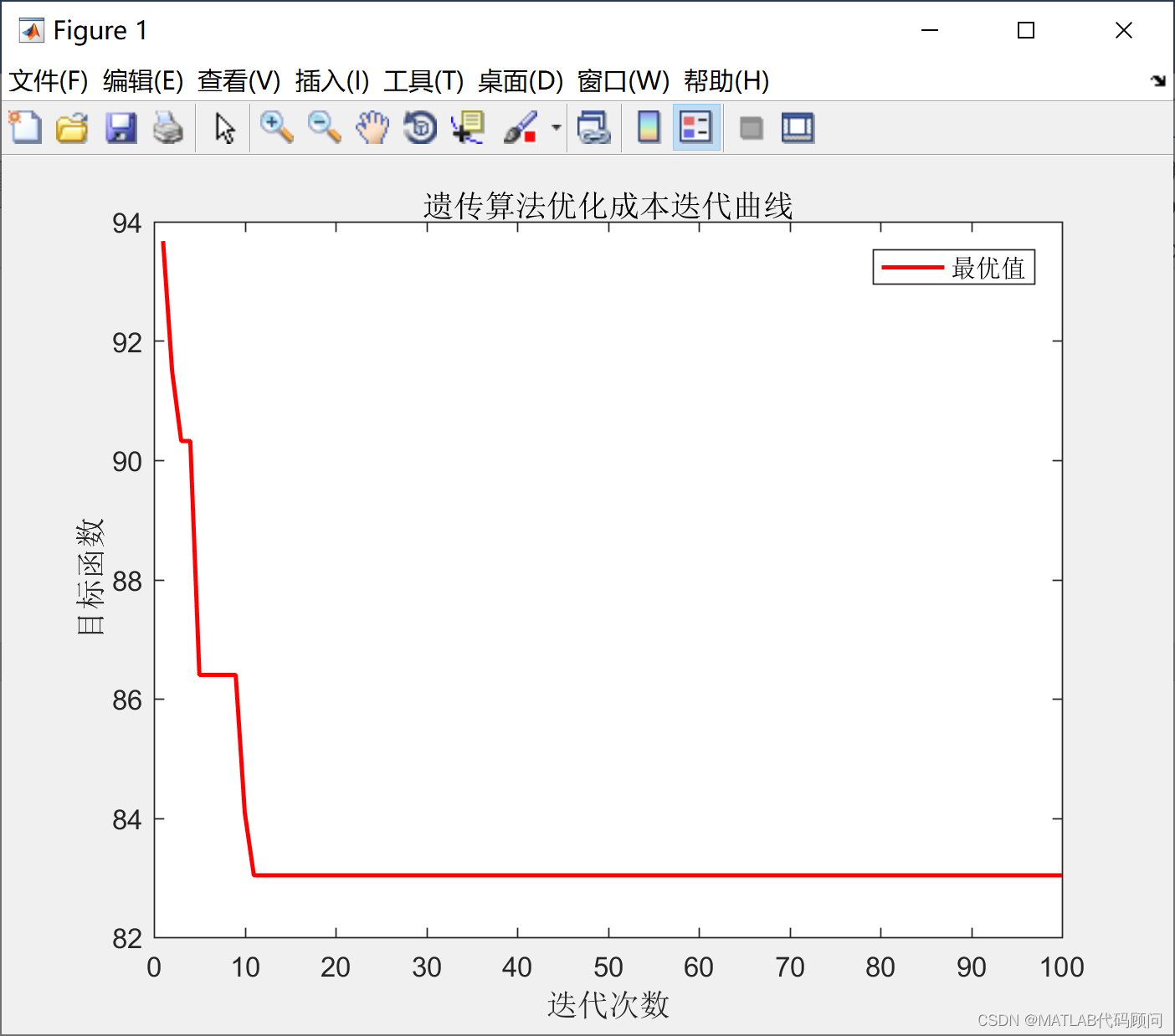
最优目标函数
bestValue =
83.0378761870964
最优染色体
bestChrom =
1 8 5 2 9 4 6 7 10 3
显示各个路径
route =
0 1 8 5 2 0
route =
0 9 4 6 7 0
route =
0 10 3 0
>>