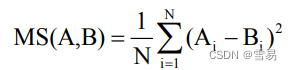前言

为提高风电场的供电质量同时增加其发电效益,利用储能技术为风电场配置一个蓄能系统是比较重要的解决措施之一。风电的蓄能技术有水力蓄能、压缩空气蓄能、超导磁力蓄能、流体电池组、电解水制氢等，其中水力蓄能是技术较成熟的一种蓄能方式，且小型的水力发电系统投资也不大，因此为采用风-水电联合供电模式不失为一种优选的方案。

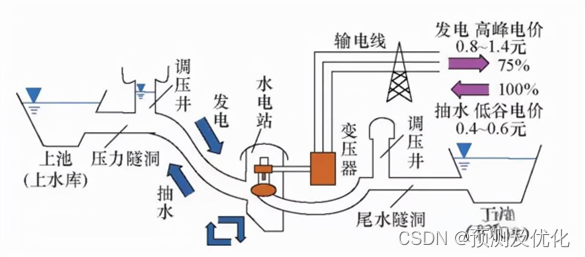
风-水联合优化模型

假定风电场在没有配置水力蓄能系统时的初始功率输出和配置水力蓄能系统后的水电机组容量均是确定的。根据我国风电产业发展的国情，我们以增加风电场的效益以及平滑风电场功率输出为目的建立目标函数：目标函数描述的是一个效益最大化的模型，寻求的是在一定的风能资源前提下如何优化调度风电场中风力发电机组、水泵和水力发电机组在各个时段的出力值以便获取风电场的最大利润和平滑风电场输出。模型中暂不考虑一些固定成本，比如水力蓄能系统的固定投资成本以及可能涉及的一些其它固定投资成本。

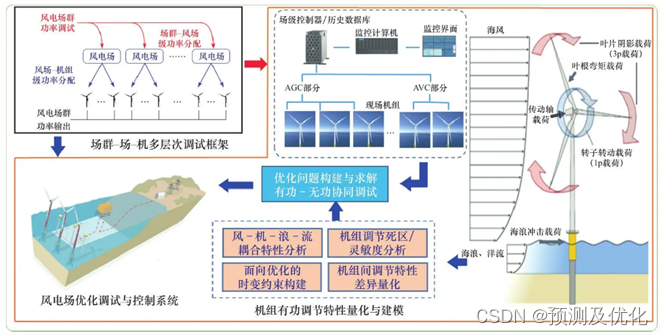
基于局部弹性搜索的混合遗传算法

所谓的概率遍历搜索法即在变量的取值范围内按照一定的精度要求，将连续区间转化为离散区间，然后对于区间内的离散点在一定的保证概率(如0.99)下求得需要搜索的次数，然后按此搜索次数参与全局寻优,最后获得符合一定精度的最优解。

遗传算法操作的是一群编码化的可行解，称作种群。它通过种群的更新与迭代来搜索全局最优解。种群的迭代是通过选择、交叉和变异等具有生物意义的遗传算子来实现的。鉴于有关遗传算法的推文已经介绍的比较多，在此就不再赘述。不过特别需要指出的是，遗传算法在进行优化时，一般涉及的变量都是独立的，并且其取值范围都是已知的，而在本程序所涉及的风-水电联合优化运行问题中，3个变量却相互制约，每一个变量的取值都有可能影响另外两个变量的取值，而且变量的取值范围也是随时变化的，这就为遗传算法的实现带来了很大的难度。程序在处理这个问题时采取了一种概率遍历搜索的方法，取得了满意的效果。

程序提出的基于局部弹性收缩的混合遗传算法采取先用遗传算法进行全局寻优，找到初步最优解后，以此最优解为初值，再用弹性搜索法求得最终的全局最优解的方法。下面就对局部弹性搜索法做一简单的说明。

假设x∈[a,b]，通过遗传算法求得x的初步最优解是x，适应度评价函数为f(x)，则局部弹性搜索的步骤如下：

1)设置指向系数sign(控制搜索的方向)初始值为0：

2)求得x，与上下边界的距离的最小值，即d1=x1-a；d2=b-x1，D=min(d1,d2)；

3)步长Δx=Dx(-1)sign(1-nb/N)；N为局部弹性搜索的总次数，n为第n次搜索，b为弹性系数(控制搜索的精度)；

4)x(n)=x1+Δx，并计算新的适应度函数值f(x(n))，如果f(x(nn))>f(x1)则sign=0，x1=x(n)则sign=1;

5)n=n+1,返回到第(2)步循环执行；

程序介绍

程序提出的基于遗传算法的风-水电联合优化运行就是采用水力蓄能的方式，为风电场配置一个水力发电系统，当可利用风能数值较大时，将一部分风能通过水泵以水能的形式储存于水库中，然后在可利用风能数值较小或上网电价较高时再经过水电发电机组将存储的能量输送到电网中去，以此实现风电场功率的优化输出，这样一方面平滑了风电场的输出波动，另一方面也充分利用了风能，增加了风电场的效益。程序中算例丰富，注释清晰，干货满满，创新性和可扩展性很高，足以撑起一篇高水平论文！下面对程序做简要介绍！

程序适用平台：Matlab+Yalmip+Cplex

程序结果

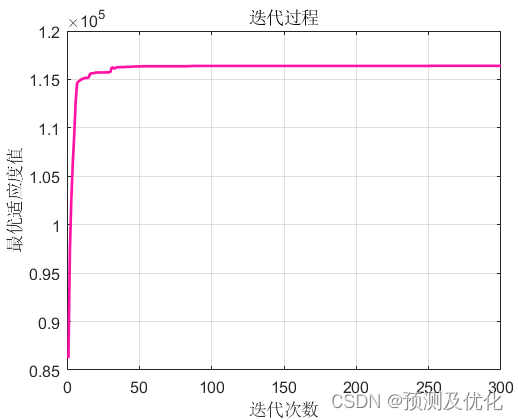
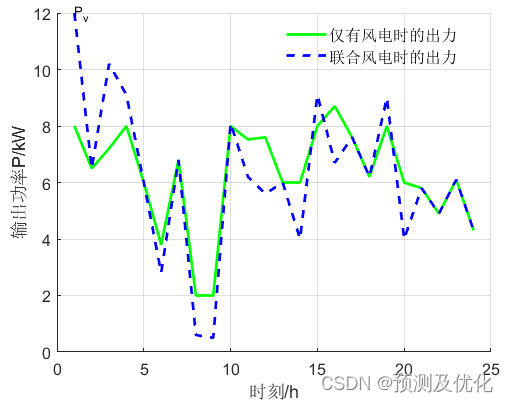
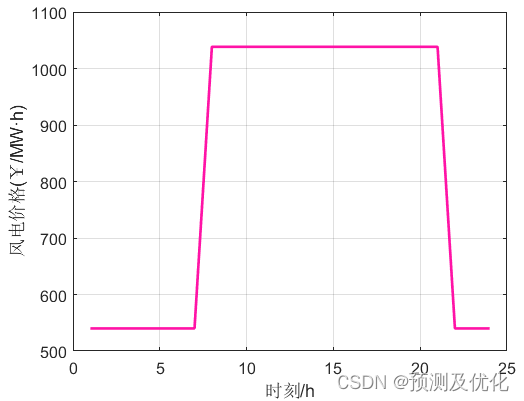
部分程序

VStepPp=rand(sizepop,NVAR)*(Vmax-Vmin)+Vmin;                                  %初始化速度
%确定风机功率P_w的取值范围-​
Pwmax=min(P_max,P_v)';       ​%[0,min(8,Pv)]
Pwmin=P_gmin*ones(1,NVAR);   ​%初始化速度
%-​确定水力发电功率P_h的取值范围
Phmax=P_hmax*ones(1,NVAR);    %[0,3]​
%% 优化
F=fun(P_w,P_h,P_p,sizepop,NVAR,C,C_p);   ​ %计算目标函数（适应度值）
E=zeros(sizepop,NVAR+1);
%-对不符合条件的解（粒子）加上惩罚因子​
%判断哪些解需要加入惩罚因子​
% 约束条件（2）            
​for nvar=1:NVAR
if P(j,nvar)>P_max​%flag=1时表示不满足约束条件
F(j)=F(j)-M;     %加上惩罚因子​%flag=1时表示不满足约束条件
F(j)=F(j)-M;   %加上惩罚因子​
% 约束条件（3）​if P_p(j,nvar)+P_w(j,nvar)>P_gmaxF(j)=F(j)-M;
if P_p(j,nvar)+P_w(j,nvar)<P_gmin​
% 约束条件（4）
if P_h(j,nvar)>min(P_hmax,E(j,nvar)*eta_h/t)F(j)=F(j)-M;​
E(j,nvar+1)=E(j,nvar)+t*(eta_p*P_p(j,nvar)-P_h(j,nvar)/eta_h);         %下一时刻水库储能​
% 约束条件（6）        ​
% 约束条件（5）
​if P_p(j,nvar)>P_pmaxF(j)=F(j)-M;
if P_p(j,nvar)<P_pmin F(j)=F(j)-M;​
% 约束条件（7）if P_v(nvar)-P_w(j,nvar)-P_p(j,nvar)<0F(j)=F(j)-M;​
%附加约束条件（1）​
if P_h(j,nvar)*P_p(j,nvar)~=0F(j)=F(j)-M*(P_h(j,nvar)*P_p(j,nvar));​
% 个体极值和群体极值（初始情况）
[bestfitness,I]=max(F);   ​ %找出最大的惩罚函数：bestfitness为惩罚函数值；I为序号数
zbest=Vary(I,:);           ​%全局最佳
gbest=Vary;                ​%个体最佳
fitnessgbest=F;            ​%个体最佳适应度值
fitnesszbest=bestfitness;  %全局最佳适应度值

部分内容源自网络，侵权联系删除！

欢迎感兴趣的小伙伴关注并私信获取完整版代码，小编会不定期更新高质量的学习资料、文章和程序代码，为您的科研加油助力！